1.4.1用空间向量研究直线、平面的位置关系(2)-【新教材】人教A版(2019)高中数学选择性必修第一册课件(共19张PPT)
文档属性
| 名称 | 1.4.1用空间向量研究直线、平面的位置关系(2)-【新教材】人教A版(2019)高中数学选择性必修第一册课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 353.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 14:04:08 | ||
图片预览




文档简介
用向量研究直线、平面的位置关系 第二课时
复习回顾
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置关系
向量表示
线线平行
线面平行
面面平行
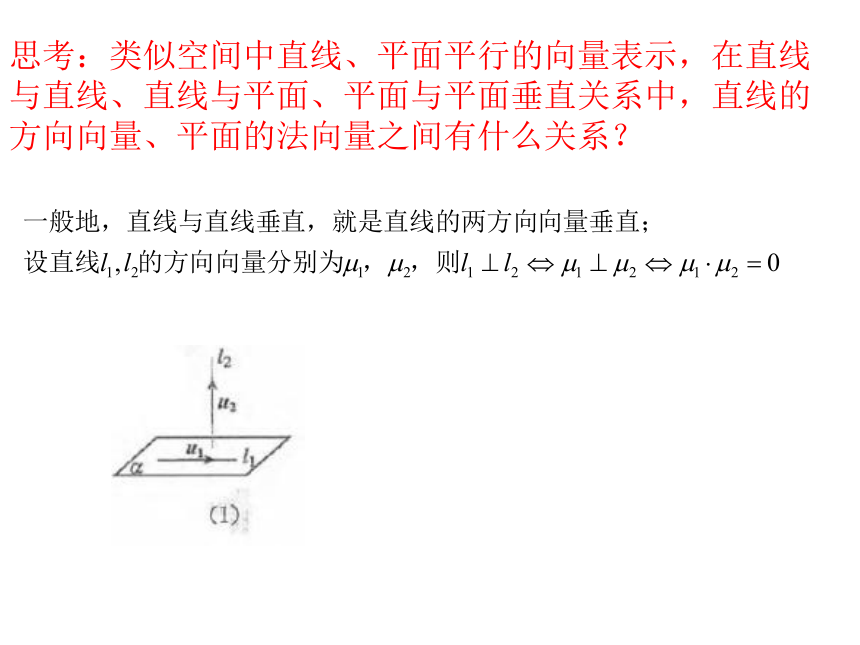
思考:类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面垂直关系中,直线的方向向量、平面的法向量之间有什么关系?
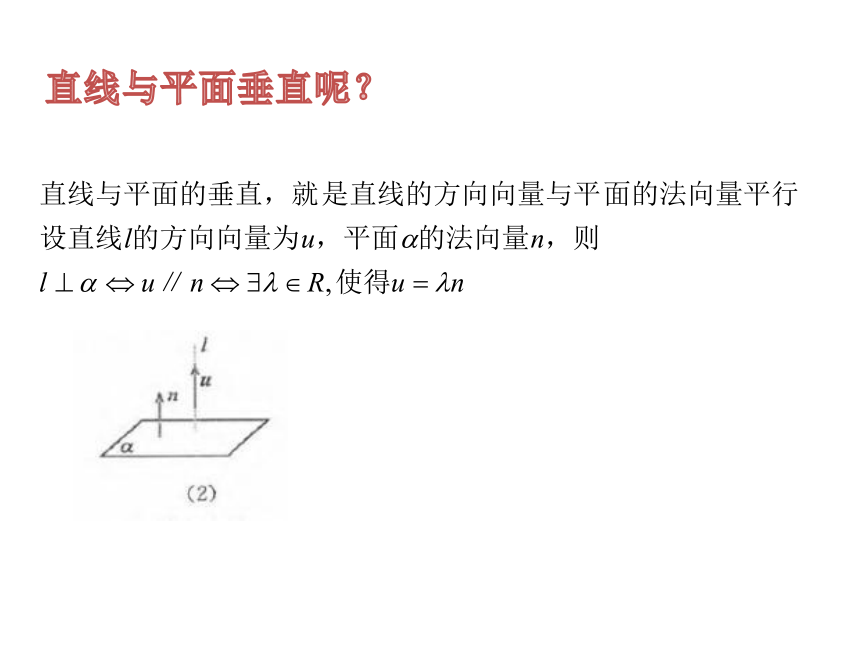
直线与平面垂直呢?
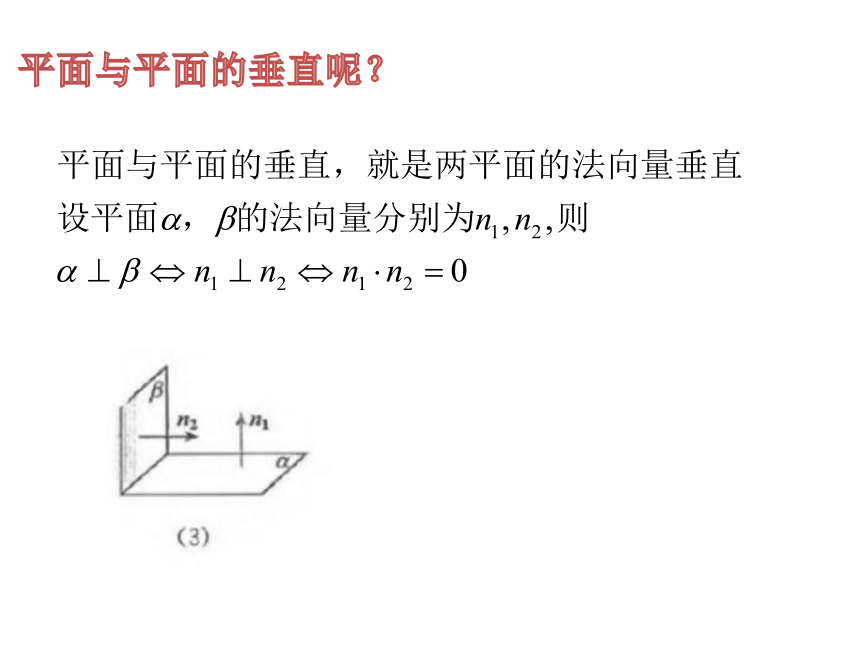
平面与平面的垂直呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置关系
向量表示
线线垂直
线面垂直
面面垂直
归纳
1.若两直线方向向量的数量积为0,则这两条直线一定垂直相交.
2.若一直线与平面垂直,则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.
3.两个平面垂直,则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直.
4.若点A,B是平面α上的任意两点, 是平面α的法向量,则
5.若向量 为平面α的法向量,则以这两个向量为方向向量的两条不重合直线一定平行.
6.一个平面的法向量有无限多个,它们互相平行.
自我检测
1、× 2、√ 3、× 4、√ 5、√ 6、√
2.若直线l的方向向量为a=(1,0,2),平面α的法向量为μ=(-2,0,-4),则( ) A.l∥α B.l⊥α C.l?α D.l与α斜交
答案:B
3.已知空间三点A(0,0,1),B(-1,1,1),C(1,2,-3),若直线AB上一点M,满足CM⊥AB,则点M的坐标为________.
例1.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
求证:(1)AE⊥CD;
证明:(1)易知AB,AD,AP两两垂直,建立如图所示的空间直角坐标系.
设PA=AB=BC=1,则A(0,0,0),B(1,0,0),P(0,0,1).
因为∠ABC=60°,所以△ABC为正三角形,所以
证:如图,取BC,B1C1的中点O,O1,连接AO,OO1.
因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABC-A1B1C1中,O,O1都为中点,所以OB⊥OO1.
又平面ABC⊥平面BCC1B1,
所以AO⊥平面BCC1B1,所以AO⊥OO1.
例2.如图,正三棱柱ABC-A1B1C1的所有侧棱长及底面边长都为2,D为CC1的中点.求证:AB1⊥平面A1BD.
证明:(1)如图所示,以A为坐标原点,AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系A-xyz.
设PA=AD=a,AB=b,
则有P(0,0,a),A(0,0,0),D(0,a,0),C(b,a,0),B(b,0,0).
∵M,N分别为AB,PC的中点,
例3.如图所示,已知PA⊥平面ABCD,四边形ABCD为矩形,PA=AD,M,N分别为AB,PC的中点.
求证:(1)MN∥平面PAD;
(2)平面PMC⊥平面PDC.
方法技巧利用空间向量证明垂直关系的方法
(1)证明两条直线垂直,只需证明两直线的方向向量垂直.
(2)证明线面垂直的方法:①证明直线的方向向量与平面的法向量平行;②转化为线线垂直问题.
(3)证明面面垂直的方法:①证明两个平面的法向量互相垂直;②转化为线面垂直、线线垂直问题.
变式训练 已知正方体ABCD-A1B1C1D1,求证:
(1)AD1∥平面BDC1; (2)A1C⊥平面BDC1.
证明:以D为坐标原点,建立如图所示的空间直角坐标系Dxyz.
设正方体的棱长为1,则有
复习回顾
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置关系
向量表示
线线平行
线面平行
面面平行
思考:类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面垂直关系中,直线的方向向量、平面的法向量之间有什么关系?
直线与平面垂直呢?
平面与平面的垂直呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置关系
向量表示
线线垂直
线面垂直
面面垂直
归纳
1.若两直线方向向量的数量积为0,则这两条直线一定垂直相交.
2.若一直线与平面垂直,则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.
3.两个平面垂直,则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直.
4.若点A,B是平面α上的任意两点, 是平面α的法向量,则
5.若向量 为平面α的法向量,则以这两个向量为方向向量的两条不重合直线一定平行.
6.一个平面的法向量有无限多个,它们互相平行.
自我检测
1、× 2、√ 3、× 4、√ 5、√ 6、√
2.若直线l的方向向量为a=(1,0,2),平面α的法向量为μ=(-2,0,-4),则( ) A.l∥α B.l⊥α C.l?α D.l与α斜交
答案:B
3.已知空间三点A(0,0,1),B(-1,1,1),C(1,2,-3),若直线AB上一点M,满足CM⊥AB,则点M的坐标为________.
例1.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
求证:(1)AE⊥CD;
证明:(1)易知AB,AD,AP两两垂直,建立如图所示的空间直角坐标系.
设PA=AB=BC=1,则A(0,0,0),B(1,0,0),P(0,0,1).
因为∠ABC=60°,所以△ABC为正三角形,所以
证:如图,取BC,B1C1的中点O,O1,连接AO,OO1.
因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABC-A1B1C1中,O,O1都为中点,所以OB⊥OO1.
又平面ABC⊥平面BCC1B1,
所以AO⊥平面BCC1B1,所以AO⊥OO1.
例2.如图,正三棱柱ABC-A1B1C1的所有侧棱长及底面边长都为2,D为CC1的中点.求证:AB1⊥平面A1BD.
证明:(1)如图所示,以A为坐标原点,AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系A-xyz.
设PA=AD=a,AB=b,
则有P(0,0,a),A(0,0,0),D(0,a,0),C(b,a,0),B(b,0,0).
∵M,N分别为AB,PC的中点,
例3.如图所示,已知PA⊥平面ABCD,四边形ABCD为矩形,PA=AD,M,N分别为AB,PC的中点.
求证:(1)MN∥平面PAD;
(2)平面PMC⊥平面PDC.
方法技巧利用空间向量证明垂直关系的方法
(1)证明两条直线垂直,只需证明两直线的方向向量垂直.
(2)证明线面垂直的方法:①证明直线的方向向量与平面的法向量平行;②转化为线线垂直问题.
(3)证明面面垂直的方法:①证明两个平面的法向量互相垂直;②转化为线面垂直、线线垂直问题.
变式训练 已知正方体ABCD-A1B1C1D1,求证:
(1)AD1∥平面BDC1; (2)A1C⊥平面BDC1.
证明:以D为坐标原点,建立如图所示的空间直角坐标系Dxyz.
设正方体的棱长为1,则有
