3.1.1椭圆及其标准方程-【新教材】人教A版(2019)高中数学选择性必修第一册课件(18张PPT)
文档属性
| 名称 | 3.1.1椭圆及其标准方程-【新教材】人教A版(2019)高中数学选择性必修第一册课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 14:01:44 | ||
图片预览



文档简介
(共18张PPT)
3.3.1 椭圆及其标准方程
神舟六号在进入太空后,先以远地点347公里、近地点200公里的椭圆轨道运行,后经过变轨调整为距地343公里的圆形轨道.
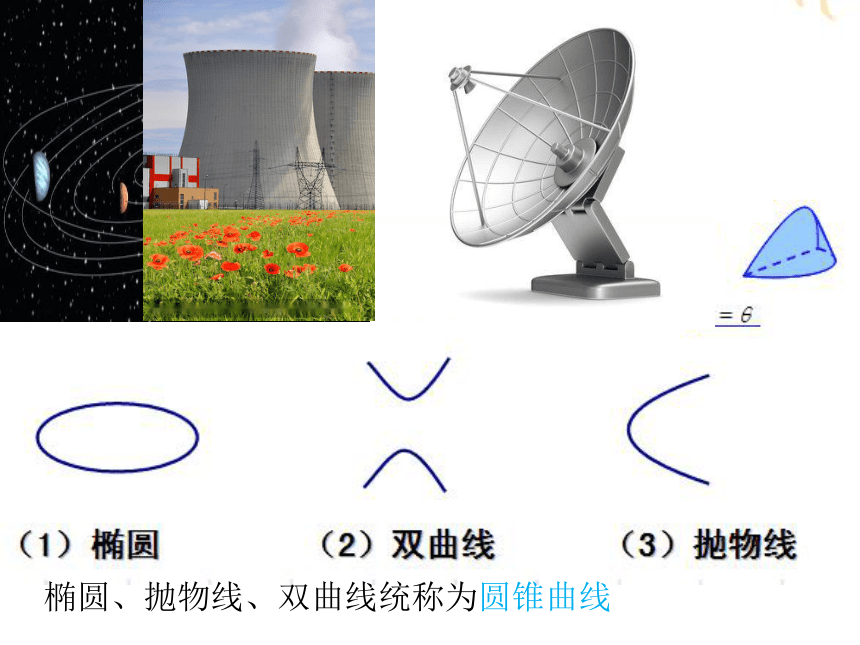
椭圆、抛物线、双曲线统称为圆锥曲线
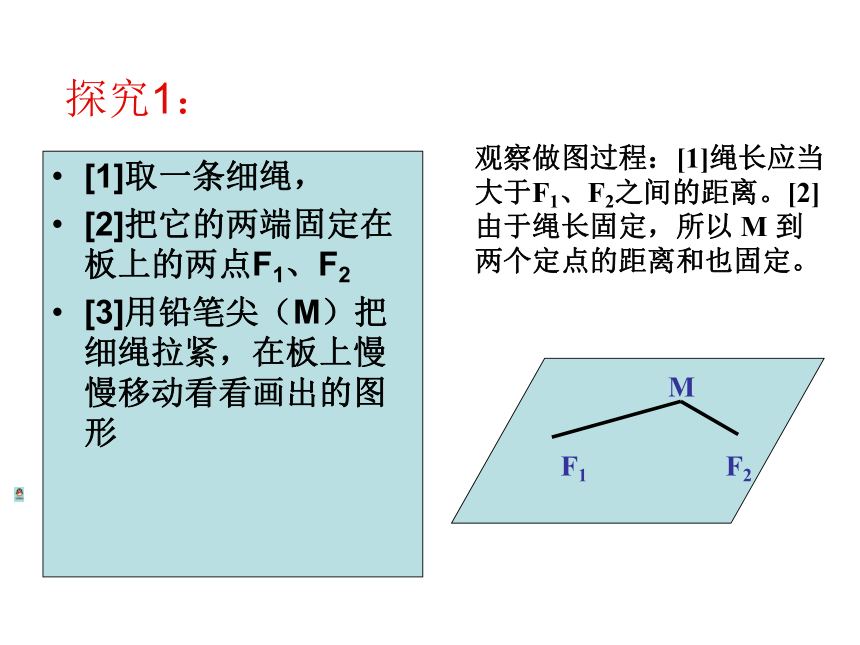
[1]取一条细绳,
[2]把它的两端固定在板上的两点F1、F2
[3]用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形
F1
F2
M
观察做图过程:[1]绳长应当大于F1、F2之间的距离。[2]由于绳长固定,所以 M 到两个定点的距离和也固定。
探究1:
平面内与两个定点F1、F2的距离的和等于常数 的点的轨迹叫做椭圆。
(2)两焦点的距离叫做椭圆的焦距(|F1F2|=2c)
一、椭圆的定义
(4)常数 2a >焦距 2C
思考:变短绳子是否一定能形成椭圆?
常数 2a =焦距 2C轨迹是线段
常数 2a <焦距 2C无轨迹
化 简
列 式
设 点
建 系
F1
F2
x
y
以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.
P( x , y )
设 P( x,y )是椭圆上任意一点
设F1F=2c,则有F1(-c,0)、F2(c,0)
F1
F2
x
y
P( x , y )
椭圆上的点满足|PF1|+|PF2|
为定值,设为2a,则2a>2c
则:
O
探究:如何建立椭圆的方程?
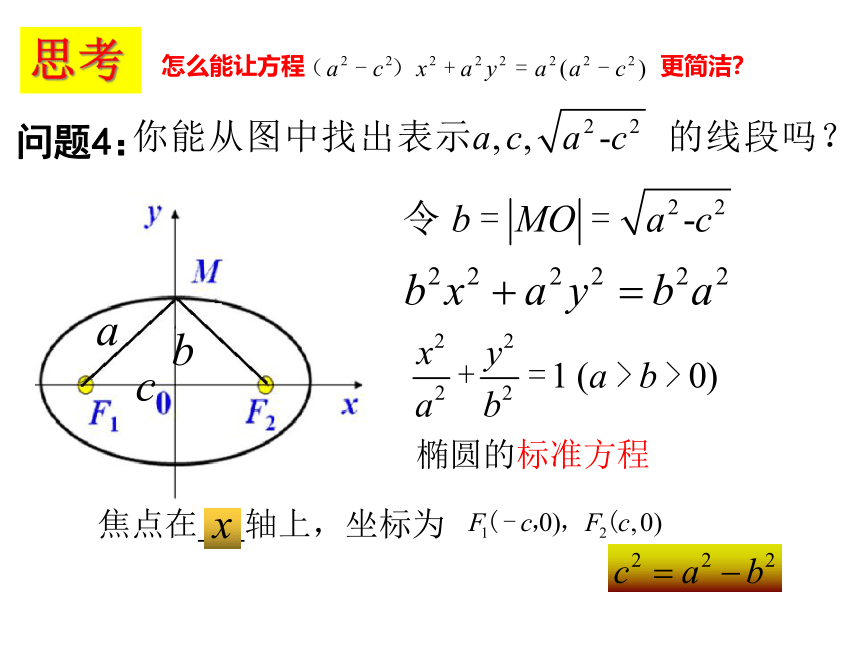
问题4:
思考
怎么能让方程 更简洁?
椭圆的标准方程
焦点在 轴上,坐标为
x
O
F1
F2
y
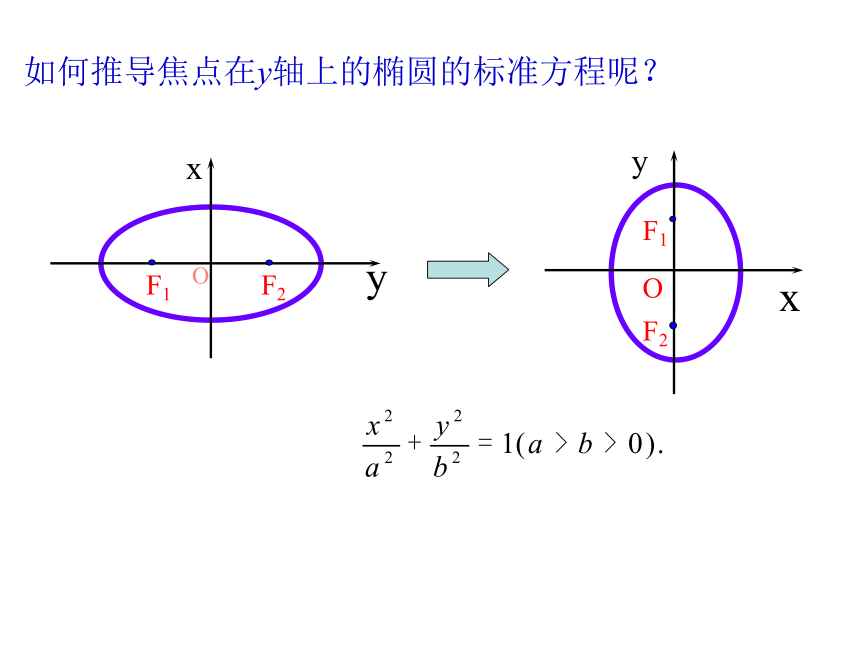
如何推导焦点在y轴上的椭圆的标准方程呢?
O
F1
F2
x
y
(2)在椭圆两种标准方程中,总有a>b>0;
x
O
F1
F2
y
二.椭圆的标准方程
O
F1
F2
y
x
(3)焦点在大分母变量所对应的那个轴上;
(1)方程的左边是两项平方和的形式,等号的右边是1;
怎样判断椭圆的焦点
在x轴上还是在y轴上?
。
典型例题
求椭圆标准方程的解题步骤:
(1)确定焦点的位置;
(2)设出椭圆的标准方程;
(3)用待定系数法确定a、b的值,写出椭圆的标准方程.
(焦点的位置不确定时要讨论)
.
例3. 已知椭圆的两焦点为F1(0,2)、F2(0,-2),并且椭圆过点 ,求椭圆的标准方程。
解法一:
解法二:
反思总结
标准方程
图形
焦点坐标
定义
a、b、c的关系
焦点位置的判定
共同点
不同点
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
b2 = a2 –c2
椭圆的两种标准方程中,总是 a>b>0. 所以哪个项的分母大,焦点就在那个轴上;反过来,焦点在哪个轴上,相应的那个项的分母就越大.
x
y
o
x
y
o
3.3.1 椭圆及其标准方程
神舟六号在进入太空后,先以远地点347公里、近地点200公里的椭圆轨道运行,后经过变轨调整为距地343公里的圆形轨道.
椭圆、抛物线、双曲线统称为圆锥曲线
[1]取一条细绳,
[2]把它的两端固定在板上的两点F1、F2
[3]用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形
F1
F2
M
观察做图过程:[1]绳长应当大于F1、F2之间的距离。[2]由于绳长固定,所以 M 到两个定点的距离和也固定。
探究1:
平面内与两个定点F1、F2的距离的和等于常数 的点的轨迹叫做椭圆。
(2)两焦点的距离叫做椭圆的焦距(|F1F2|=2c)
一、椭圆的定义
(4)常数 2a >焦距 2C
思考:变短绳子是否一定能形成椭圆?
常数 2a =焦距 2C轨迹是线段
常数 2a <焦距 2C无轨迹
化 简
列 式
设 点
建 系
F1
F2
x
y
以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.
P( x , y )
设 P( x,y )是椭圆上任意一点
设F1F=2c,则有F1(-c,0)、F2(c,0)
F1
F2
x
y
P( x , y )
椭圆上的点满足|PF1|+|PF2|
为定值,设为2a,则2a>2c
则:
O
探究:如何建立椭圆的方程?
问题4:
思考
怎么能让方程 更简洁?
椭圆的标准方程
焦点在 轴上,坐标为
x
O
F1
F2
y
如何推导焦点在y轴上的椭圆的标准方程呢?
O
F1
F2
x
y
(2)在椭圆两种标准方程中,总有a>b>0;
x
O
F1
F2
y
二.椭圆的标准方程
O
F1
F2
y
x
(3)焦点在大分母变量所对应的那个轴上;
(1)方程的左边是两项平方和的形式,等号的右边是1;
怎样判断椭圆的焦点
在x轴上还是在y轴上?
。
典型例题
求椭圆标准方程的解题步骤:
(1)确定焦点的位置;
(2)设出椭圆的标准方程;
(3)用待定系数法确定a、b的值,写出椭圆的标准方程.
(焦点的位置不确定时要讨论)
.
例3. 已知椭圆的两焦点为F1(0,2)、F2(0,-2),并且椭圆过点 ,求椭圆的标准方程。
解法一:
解法二:
反思总结
标准方程
图形
焦点坐标
定义
a、b、c的关系
焦点位置的判定
共同点
不同点
F1(-c,0)、F2(c,0)
F1(0,-c)、F2(0,c)
平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
b2 = a2 –c2
椭圆的两种标准方程中,总是 a>b>0. 所以哪个项的分母大,焦点就在那个轴上;反过来,焦点在哪个轴上,相应的那个项的分母就越大.
x
y
o
x
y
o
