2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 05:06:30 | ||
图片预览



文档简介
2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题
一.选择题(共12小题,满分48分,每小题4分)
1.计算(﹣2020)0的结果是( )
A.2020
B.1
C.﹣2020
D.0
2.下列计算正确的是( )
A.a2?a3=a6
B.(a2)4=a8
C.a﹣2=﹣a2
D.a3÷a3=a
3.刻蚀机是芯片制造和微观加工最核心的设备之一,中国自主研发的5纳米刻蚀机已获成功,5纳米就是0.000000005米.数据0.000000005用科学记数法表示为( )
A.5×10﹣8
B.5×10﹣9
C.0.5×10﹣8
D.50×10﹣9
4.国务院决定于2020年11月1日零时开展第七次全国人口普查,人口调查采用普查方式的理由是( )
A.人口调查的数目不太大
B.人口调查需要获得全面准确的信息
C.人口调查具有破坏性
D.受条件限制,无法进行抽样调查
5.体育课上,老师测量跳远成绩的依据是( )
A.平行线间的距离相等
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
6.若实数n满足(n﹣2018)2+(2019﹣n)2=3,则(n﹣2018)(2019﹣n)的值是( )
A.1
B.
C.0
D.﹣1
7.如图,直线a、b被直线c所截,现给出下列四个条件:(1)∠1=∠5;(2)∠2+∠7=180°;(3)∠4=∠7;(4)∠3=∠6;其中能判定a∥b的条件的序号是( )
A.(1)(2)
B.(1)(3)
C.(1)(4)
D.(3)(4)
8.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1
B.2
C.3
D.4
9.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4
B.3
C.2
D.1
10.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69°
B.111°
C.141°
D.159°
11.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135°
B.120°
C.105°
D.100°
12.在同一平面内,不重合的三条直线a、b、c中,如果a⊥b,b⊥c,那么a与c的位置关系是( )
A.垂直
B.平行
C.相交
D.不能确定
二.填空题(共6小题,满分24分,每小题4分)
13.经过平面内任意三点中的两点共可以画出
条直线.
14.若x2+2(m﹣3)x+9是完全平方式,则m的值等于
.
15.钟表上的时间是3时30分,此时时针与分针所成的夹角是
度.
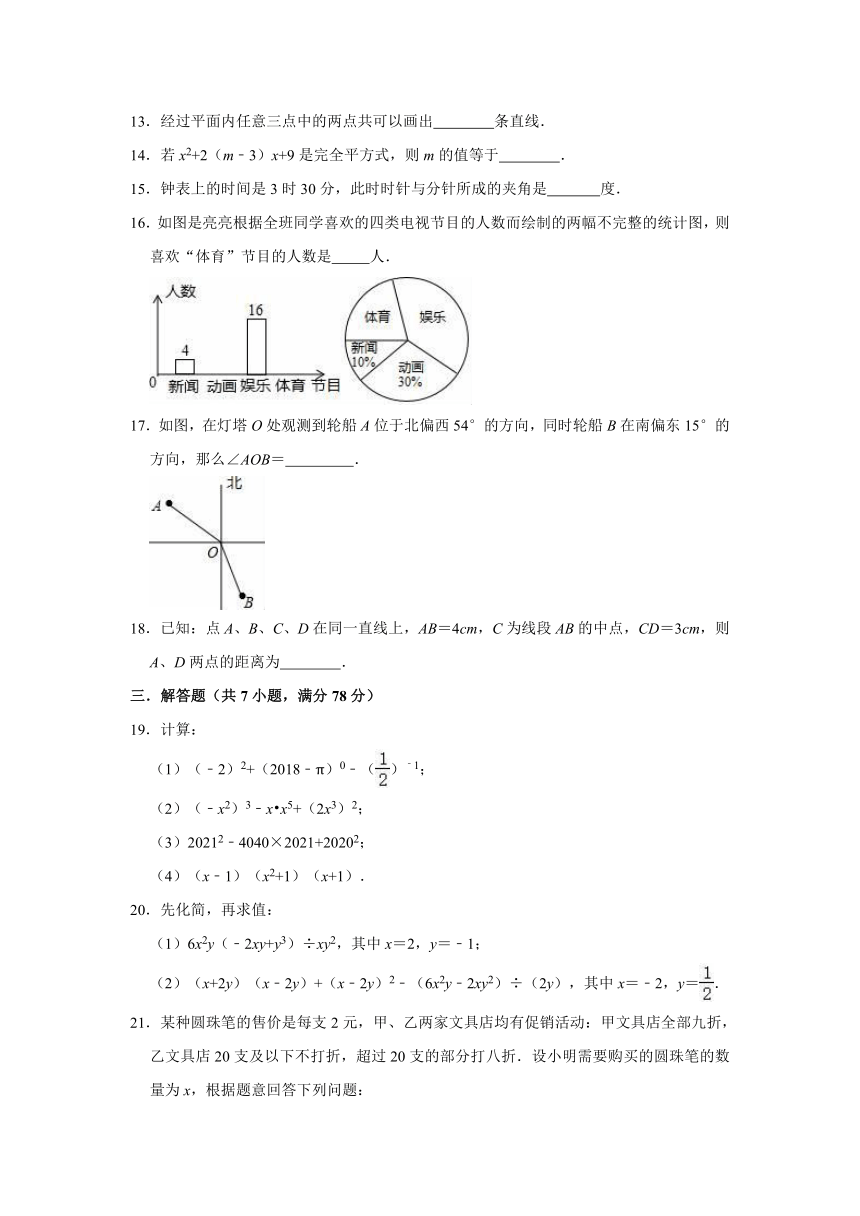
16.如图是亮亮根据全班同学喜欢的四类电视节目的人数而绘制的两幅不完整的统计图,则喜欢“体育”节目的人数是
人.
17.如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB=
.
18.已知:点A、B、C、D在同一直线上,AB=4cm,C为线段AB的中点,CD=3cm,则A、D两点的距离为
.
三.解答题(共7小题,满分78分)
19.计算:
(1)(﹣2)2+(2018﹣π)0﹣()﹣1;
(2)(﹣x2)3﹣x?x5+(2x3)2;
(3)20212﹣4040×2021+20202;
(4)(x﹣1)(x2+1)(x+1).
20.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
21.某种圆珠笔的售价是每支2元,甲、乙两家文具店均有促销活动:甲文具店全部九折,乙文具店20支及以下不打折,超过20支的部分打八折.设小明需要购买的圆珠笔的数量为x,根据题意回答下列问题:
(1)若购买超过20支的圆珠笔,则在甲文具店需要花费
元,在乙文具店需要花费
元.(用含x的代数式表示)
(2)当x=25时,选择哪家文具店更优惠?当x=50呢?
(3)随着x的变化,试说明选择哪家文具店更优惠.
22.我区的数学爱好者申请了一项省级课题﹣﹣《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如图两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:
(1)本次调查共抽取了多少名学生?并补全条形统计图;
(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?
(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?
23.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=
(
),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴
=∠CDE(
),
∠DCE=∠BEF(
),
∴
=
(等量代换),
∴EF平分∠DEB(
).
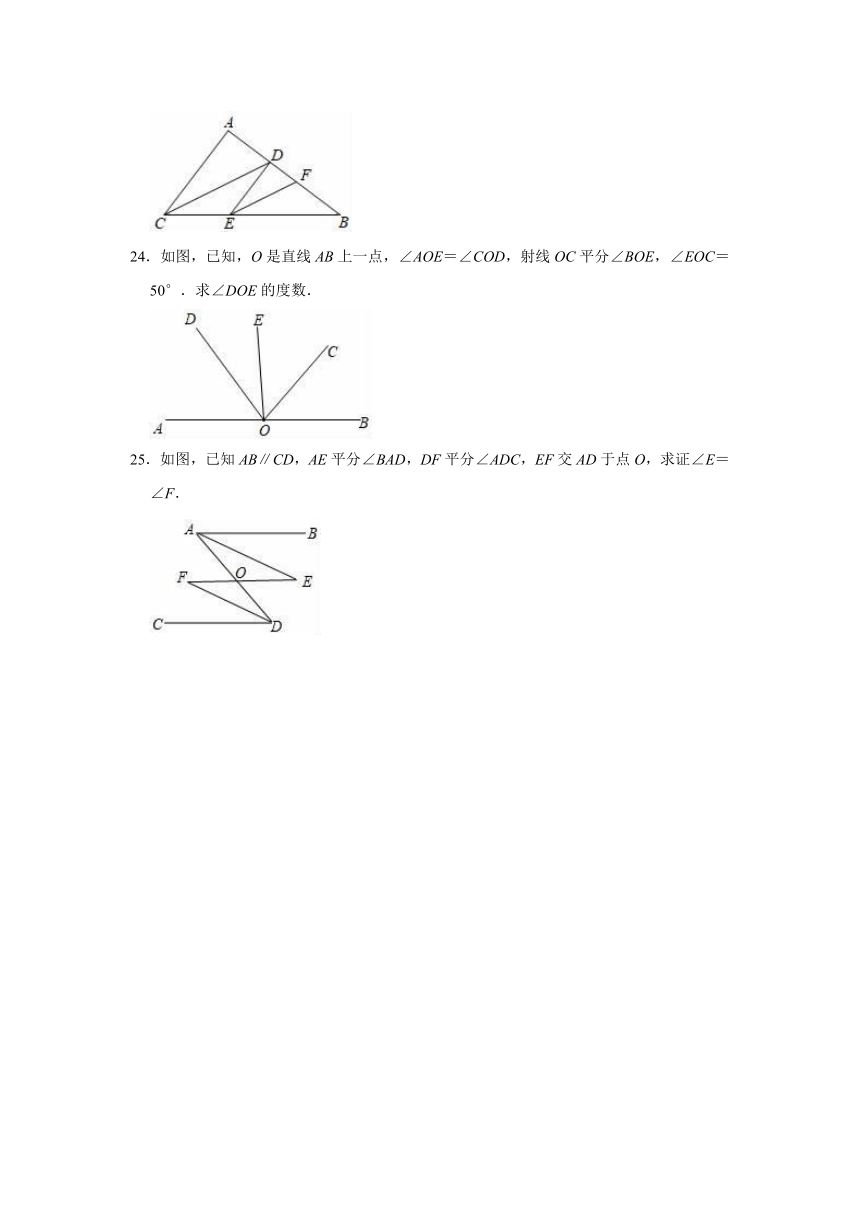
24.如图,已知,O是直线AB上一点,∠AOE=∠COD,射线OC平分∠BOE,∠EOC=50°.求∠DOE的度数.
25.如图,已知AB∥CD,AE平分∠BAD,DF平分∠ADC,EF交AD于点O,求证∠E=∠F.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:(﹣2020)0=1.
故选:B.
2.解:A、a2?a3=a5,故本选项不合题意;
B、(a2)4=a8,故本选项符合题意;
C、a﹣2=,故本选项不合题意;
D、a3÷a3=1,故本选项不合题意.
故选:B.
3.解:0.000000005=5×10﹣9.
故选:B.
4.解:国务院决定于2020年11月1日零时开展第七次全国人口普查,人口调查采用普查方式的理由是:人口调查需要获得全面准确的信息;
故选:B.
5.解:体育课上,老师测量跳远成绩的依据是垂线段最短.
故选:C.
6.解:设n﹣2018=a,2019﹣n=b,则a2+b2=3,a+b=1,
∴ab=,
=,
=﹣1.
∴(n﹣2018)(2019﹣n)=﹣1.
故选:D.
7.解:(1)∵∠1=∠5,
∴a∥b;
(2)∵∠2+∠7=180°,∠2+∠3=180°,
∴∠3=∠7,
∴a∥b;
(3)由∠4=∠7得不到a∥b;
(4)由∠3=∠6得不到a∥b,
故选:A.
8.解:①为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,这种调查采用了抽样调查的方式,故说法正确;
②7万名考生的数学成绩是总体,故原说法错误;
③每名考生的数学成绩是个体,故说法正确;
④1000名考生的数学成绩是总体的一个样本,故说法正确;
⑤1000是样本容量,故原说法错误.
所以正确的说法有3个.
故选:C.
9.解:∵AB=10cm,BC=4cm.
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
10.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°,
故选:C.
11.解:∵∠1=30°
∴∠AMA1+∠DMD1=180°﹣30°=150°
∵将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,
∴MB平分∠AMA1,MC平分∠DMD1
∴∠BMA1+∠CMD1=(∠AMA1+∠DMD1)=75°
∴∠BMC=∠1+∠BMA1+∠CMD1=30°+75°=105°
故选:C.
12.解:∵同一平面内的三条直线a,b,c,a⊥b,b⊥c,
∴a∥c,
故选:B.
二.填空题(共6小题,满分24分,每小题4分)
13.解:
不妨设三个点为A、B、C,
当三个点在同一直线上时,只能画一条,
当三个点不在同一直线上时,则有AB、AC、BC三条,
故答案为:1或3.
14.解:∵x2+2(m﹣3)x+9是完全平方式,
∴m﹣3=±3,
解得:m=6或0.
故答案为:6或0.
15.解:3点30分时,时针与分针的较小夹角是2.5个大格,
一个大格的度数是30°,所以30°×2.5=75°;
故答案为:75.
16.解:调查的总人数是:4÷10%=40(人),
喜欢动画的人数有:40×30%=12(人),
体育的人数有:40﹣4﹣12﹣16=8(人);
故答案为:8.
17.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°.
故答案为:141°.
18.解:如图所示:
①点D在线段AB的延长线上时,如图1,
∵C为线段AB的中点,AB=4cm
∴AC=BC=AB,
又∵AB=4cm,
∴BC==2cm,
又∵BD=CD﹣BC,
∴BD=3﹣2=1cm,
又∵AD=AB+BD,
∴AD=4+1=5cm;
②点D在线段AB的r反向延长线上时,如图2,
同理可得:
∴AC==2cm,
又∵CD=AC+AD,
∴AD=3﹣2=1cm,
综合所述:A、D两点的距离为1cm或5cm,
故答案为1cm或5cm.
三.解答题(共7小题,满分78分)
19.解:(1)(﹣2)2+(2018﹣π)0﹣()﹣1
=4+1﹣2
=3;
(2)(﹣x2)3﹣x?x5+(2x3)2;
=﹣x6﹣x6+4x6
=2x6;
(3)20212﹣4040×2021+20202
=(2021﹣2020)2
=1;
(4)(x﹣1)(x2+1)(x+1)
=(x2﹣1)(x2+1)
=x4﹣1.
20.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
21.解:(1)若购买超过20支的圆珠笔,则在甲文具店需要花费1.8x元,在乙文具店需要花费(1.6x+8)元;
故答案为:1.8x,1.6x+8;
(2)当x=25时,甲文具店:1.8×25=45元;乙文具店:1.6×25+8=48元,
∵45<48,
∴甲文具店更优惠;
当x=50时,甲文具店:1.8×50=90元;乙文具店:1.6×50+8=88元,
∵90>88,
∴乙文具店更优惠,
则当x=25时,选择甲文具店更优惠;当x=50时,选择乙文具店更优惠;
(3)若x<20,1.8x<2x,甲文具店更优惠;
若x>20,
当甲文具店费用更低时,1.8x<1.6x+8,
解得:x<40;
当甲乙两家文具店费用相同时,1.8x=1.6x+8,
解得:x=40;
当乙文具店费用更低时,1.8x>1.6x+8,
解得:x>40,
则当购买圆珠笔少于40支时,甲文具店更优惠;
当购买圆珠笔等于40支时,甲乙两家文具店费用相同;
当购买圆珠笔多于40支时,乙文具店更优惠.
22.解:(1)本次调查共抽取学生为:=400(名),
∴不太了解的学生为:400﹣120﹣160﹣20=100(名),
补全条形统计图如下:
(2)“理解”所占扇形的圆心角是:×360°=108°;
(3)8000×(40%+)=5600(名),
所以“理解”和“了解”的共有学生5600名.
23.证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=∠CDE(两直线平行,内错角相等),
∴∠DCE=∠CDE(
等量代换),
∵CD∥EF
(
已知
),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(
角平分线的定义
).
故答案为:∠CDE;∠DEF;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF;∠FEB;角平分线的定义.
24.解:∵∠AOE=∠COD
∴∠AOE﹣∠DOE=∠COD﹣∠DOE,
即∠AOD=∠EOC=50°
∵射线OC平分∠BOE,
∴∠EOE=∠COB=50°
∴∠DOE=180°﹣3×50°=30°.
25.证明:∵AB∥CD,
∴∠BAD=∠ADC,
∵AE平分∠BAD,DF平分∠ADC,
∴∠EAD=∠BAD,∠FDA=∠ADC,
∴∠EAD=∠FDA,
∴AE∥FD,
∴∠E=∠F.
一.选择题(共12小题,满分48分,每小题4分)
1.计算(﹣2020)0的结果是( )
A.2020
B.1
C.﹣2020
D.0
2.下列计算正确的是( )
A.a2?a3=a6
B.(a2)4=a8
C.a﹣2=﹣a2
D.a3÷a3=a
3.刻蚀机是芯片制造和微观加工最核心的设备之一,中国自主研发的5纳米刻蚀机已获成功,5纳米就是0.000000005米.数据0.000000005用科学记数法表示为( )
A.5×10﹣8
B.5×10﹣9
C.0.5×10﹣8
D.50×10﹣9
4.国务院决定于2020年11月1日零时开展第七次全国人口普查,人口调查采用普查方式的理由是( )
A.人口调查的数目不太大
B.人口调查需要获得全面准确的信息
C.人口调查具有破坏性
D.受条件限制,无法进行抽样调查
5.体育课上,老师测量跳远成绩的依据是( )
A.平行线间的距离相等
B.两点之间,线段最短
C.垂线段最短
D.两点确定一条直线
6.若实数n满足(n﹣2018)2+(2019﹣n)2=3,则(n﹣2018)(2019﹣n)的值是( )
A.1
B.
C.0
D.﹣1
7.如图,直线a、b被直线c所截,现给出下列四个条件:(1)∠1=∠5;(2)∠2+∠7=180°;(3)∠4=∠7;(4)∠3=∠6;其中能判定a∥b的条件的序号是( )
A.(1)(2)
B.(1)(3)
C.(1)(4)
D.(3)(4)
8.某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查方式是抽样调查;
②7万名考生是总体;
③每名考生的数学成绩是个体;
④1000名考生的数学成绩是总体的一个样本;
⑤1000名考生是样本容量.
A.1
B.2
C.3
D.4
9.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4
B.3
C.2
D.1
10.在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A.69°
B.111°
C.141°
D.159°
11.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,若∠1=30°,则∠BMC=( )
A.135°
B.120°
C.105°
D.100°
12.在同一平面内,不重合的三条直线a、b、c中,如果a⊥b,b⊥c,那么a与c的位置关系是( )
A.垂直
B.平行
C.相交
D.不能确定
二.填空题(共6小题,满分24分,每小题4分)
13.经过平面内任意三点中的两点共可以画出
条直线.
14.若x2+2(m﹣3)x+9是完全平方式,则m的值等于
.
15.钟表上的时间是3时30分,此时时针与分针所成的夹角是
度.
16.如图是亮亮根据全班同学喜欢的四类电视节目的人数而绘制的两幅不完整的统计图,则喜欢“体育”节目的人数是
人.
17.如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB=
.
18.已知:点A、B、C、D在同一直线上,AB=4cm,C为线段AB的中点,CD=3cm,则A、D两点的距离为
.
三.解答题(共7小题,满分78分)
19.计算:
(1)(﹣2)2+(2018﹣π)0﹣()﹣1;
(2)(﹣x2)3﹣x?x5+(2x3)2;
(3)20212﹣4040×2021+20202;
(4)(x﹣1)(x2+1)(x+1).
20.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
21.某种圆珠笔的售价是每支2元,甲、乙两家文具店均有促销活动:甲文具店全部九折,乙文具店20支及以下不打折,超过20支的部分打八折.设小明需要购买的圆珠笔的数量为x,根据题意回答下列问题:
(1)若购买超过20支的圆珠笔,则在甲文具店需要花费
元,在乙文具店需要花费
元.(用含x的代数式表示)
(2)当x=25时,选择哪家文具店更优惠?当x=50呢?
(3)随着x的变化,试说明选择哪家文具店更优惠.
22.我区的数学爱好者申请了一项省级课题﹣﹣《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如图两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:
(1)本次调查共抽取了多少名学生?并补全条形统计图;
(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?
(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?
23.填空:(将下面的推理过程及依据补充完整)
如图,已知:CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=
(
),
∴∠DCE=∠CDE(等量代换),
∵CD∥EF(已知),
∴
=∠CDE(
),
∠DCE=∠BEF(
),
∴
=
(等量代换),
∴EF平分∠DEB(
).
24.如图,已知,O是直线AB上一点,∠AOE=∠COD,射线OC平分∠BOE,∠EOC=50°.求∠DOE的度数.
25.如图,已知AB∥CD,AE平分∠BAD,DF平分∠ADC,EF交AD于点O,求证∠E=∠F.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:(﹣2020)0=1.
故选:B.
2.解:A、a2?a3=a5,故本选项不合题意;
B、(a2)4=a8,故本选项符合题意;
C、a﹣2=,故本选项不合题意;
D、a3÷a3=1,故本选项不合题意.
故选:B.
3.解:0.000000005=5×10﹣9.
故选:B.
4.解:国务院决定于2020年11月1日零时开展第七次全国人口普查,人口调查采用普查方式的理由是:人口调查需要获得全面准确的信息;
故选:B.
5.解:体育课上,老师测量跳远成绩的依据是垂线段最短.
故选:C.
6.解:设n﹣2018=a,2019﹣n=b,则a2+b2=3,a+b=1,
∴ab=,
=,
=﹣1.
∴(n﹣2018)(2019﹣n)=﹣1.
故选:D.
7.解:(1)∵∠1=∠5,
∴a∥b;
(2)∵∠2+∠7=180°,∠2+∠3=180°,
∴∠3=∠7,
∴a∥b;
(3)由∠4=∠7得不到a∥b;
(4)由∠3=∠6得不到a∥b,
故选:A.
8.解:①为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,这种调查采用了抽样调查的方式,故说法正确;
②7万名考生的数学成绩是总体,故原说法错误;
③每名考生的数学成绩是个体,故说法正确;
④1000名考生的数学成绩是总体的一个样本,故说法正确;
⑤1000是样本容量,故原说法错误.
所以正确的说法有3个.
故选:C.
9.解:∵AB=10cm,BC=4cm.
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
10.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°,
故选:C.
11.解:∵∠1=30°
∴∠AMA1+∠DMD1=180°﹣30°=150°
∵将纸片沿BM,CM折叠,使点A落在点A1处,点D落在点D1处,
∴MB平分∠AMA1,MC平分∠DMD1
∴∠BMA1+∠CMD1=(∠AMA1+∠DMD1)=75°
∴∠BMC=∠1+∠BMA1+∠CMD1=30°+75°=105°
故选:C.
12.解:∵同一平面内的三条直线a,b,c,a⊥b,b⊥c,
∴a∥c,
故选:B.
二.填空题(共6小题,满分24分,每小题4分)
13.解:
不妨设三个点为A、B、C,
当三个点在同一直线上时,只能画一条,
当三个点不在同一直线上时,则有AB、AC、BC三条,
故答案为:1或3.
14.解:∵x2+2(m﹣3)x+9是完全平方式,
∴m﹣3=±3,
解得:m=6或0.
故答案为:6或0.
15.解:3点30分时,时针与分针的较小夹角是2.5个大格,
一个大格的度数是30°,所以30°×2.5=75°;
故答案为:75.
16.解:调查的总人数是:4÷10%=40(人),
喜欢动画的人数有:40×30%=12(人),
体育的人数有:40﹣4﹣12﹣16=8(人);
故答案为:8.
17.解:由题意得:∠1=54°,∠2=15°,
∠3=90°﹣54°=36°,
∠AOB=36°+90°+15°=141°.
故答案为:141°.
18.解:如图所示:
①点D在线段AB的延长线上时,如图1,
∵C为线段AB的中点,AB=4cm
∴AC=BC=AB,
又∵AB=4cm,
∴BC==2cm,
又∵BD=CD﹣BC,
∴BD=3﹣2=1cm,
又∵AD=AB+BD,
∴AD=4+1=5cm;
②点D在线段AB的r反向延长线上时,如图2,
同理可得:
∴AC==2cm,
又∵CD=AC+AD,
∴AD=3﹣2=1cm,
综合所述:A、D两点的距离为1cm或5cm,
故答案为1cm或5cm.
三.解答题(共7小题,满分78分)
19.解:(1)(﹣2)2+(2018﹣π)0﹣()﹣1
=4+1﹣2
=3;
(2)(﹣x2)3﹣x?x5+(2x3)2;
=﹣x6﹣x6+4x6
=2x6;
(3)20212﹣4040×2021+20202
=(2021﹣2020)2
=1;
(4)(x﹣1)(x2+1)(x+1)
=(x2﹣1)(x2+1)
=x4﹣1.
20.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
21.解:(1)若购买超过20支的圆珠笔,则在甲文具店需要花费1.8x元,在乙文具店需要花费(1.6x+8)元;
故答案为:1.8x,1.6x+8;
(2)当x=25时,甲文具店:1.8×25=45元;乙文具店:1.6×25+8=48元,
∵45<48,
∴甲文具店更优惠;
当x=50时,甲文具店:1.8×50=90元;乙文具店:1.6×50+8=88元,
∵90>88,
∴乙文具店更优惠,
则当x=25时,选择甲文具店更优惠;当x=50时,选择乙文具店更优惠;
(3)若x<20,1.8x<2x,甲文具店更优惠;
若x>20,
当甲文具店费用更低时,1.8x<1.6x+8,
解得:x<40;
当甲乙两家文具店费用相同时,1.8x=1.6x+8,
解得:x=40;
当乙文具店费用更低时,1.8x>1.6x+8,
解得:x>40,
则当购买圆珠笔少于40支时,甲文具店更优惠;
当购买圆珠笔等于40支时,甲乙两家文具店费用相同;
当购买圆珠笔多于40支时,乙文具店更优惠.
22.解:(1)本次调查共抽取学生为:=400(名),
∴不太了解的学生为:400﹣120﹣160﹣20=100(名),
补全条形统计图如下:
(2)“理解”所占扇形的圆心角是:×360°=108°;
(3)8000×(40%+)=5600(名),
所以“理解”和“了解”的共有学生5600名.
23.证明:∵CD平分∠ACB(已知),
∴∠DCA=∠DCE(角平分线的定义),
∵AC∥DE(已知),
∴∠DCA=∠CDE(两直线平行,内错角相等),
∴∠DCE=∠CDE(
等量代换),
∵CD∥EF
(
已知
),
∴∠DEF=∠CDE(两直线平行,内错角相等),
∠DCE=∠FEB(两直线平行,同位角相等),
∴∠DEF=∠FEB(等量代换),
∴EF平分∠DEB(
角平分线的定义
).
故答案为:∠CDE;∠DEF;两直线平行,内错角相等;两直线平行,同位角相等;∠DEF;∠FEB;角平分线的定义.
24.解:∵∠AOE=∠COD
∴∠AOE﹣∠DOE=∠COD﹣∠DOE,
即∠AOD=∠EOC=50°
∵射线OC平分∠BOE,
∴∠EOE=∠COB=50°
∴∠DOE=180°﹣3×50°=30°.
25.证明:∵AB∥CD,
∴∠BAD=∠ADC,
∵AE平分∠BAD,DF平分∠ADC,
∴∠EAD=∠BAD,∠FDA=∠ADC,
∴∠EAD=∠FDA,
∴AE∥FD,
∴∠E=∠F.
同课章节目录
