2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 05:08:24 | ||
图片预览



文档简介
2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题
一.选择题(共10小题,满分30分,每小题3分)
1.若二元一次方程3x﹣y=7,2x+3y=1,y=kx﹣9有公共解,则k的取值为( )
A.3
B.﹣3
C.﹣4
D.4
2.下列命题中:①同旁内角互补,两直线平行;②如果两个实数相等,那么它们的平方相等;③如果两个角是直角,那么它们相等;④全等三角形的对应边相等.逆命题不成立的是( )
A.①②
B.①②③
C.②③
D.②③④
3.下列语句中描述的事件必然发生的是( )
A.15个人中至少有两个人同月出生
B.一位同学在打篮球,投篮一次就投中
C.在1,2,3,4中任取两个数,它们的和大于7
D.掷一枚硬币,正面朝上
4.在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+θ,则∠BOC=( )
A.90°﹣θ
B.2θ
C.180°﹣θ
D.以上答案都不对
5.有两个可以自由转动的转盘,每个转盘被分成如图所示的几个扇形,游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
A.两个转盘转出蓝色的概率一样大
B.如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C.先转动A转盘再转动B转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D.游戏者配成紫色的概率为
6.小李家去年节余50000元,今年可节余95000元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为x元,支出为y元,则可列方程组为( )
A.
B.
C.
D.
7.下列命题:①有理数与数轴上的点一一对应;②过一点有且只有一条直线与已知直线平行;③从直线外一点到这条直线的垂线段叫做点到直线的距离;④负数没有平方根.其中是真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
8.已知等边三角形的边长为4,则其面积为( )平方单位.
A.4
B.8
C.12
D.16
9.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH长为( )
A.3
B.4
C.5
D.6
10.下列说法正确的有:①等腰三角形的高、中线、角平分线互相重合;②等边三角形是等腰三角形;③若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形;④等腰三角形的两个底角相等;
⑤一腰和一腰上的高对应相等的两个等腰三角形全等.其中正确的共有( )
A.5个
B.4个
C.3个
D.2个
二.填空题(共8小题,满分28分)
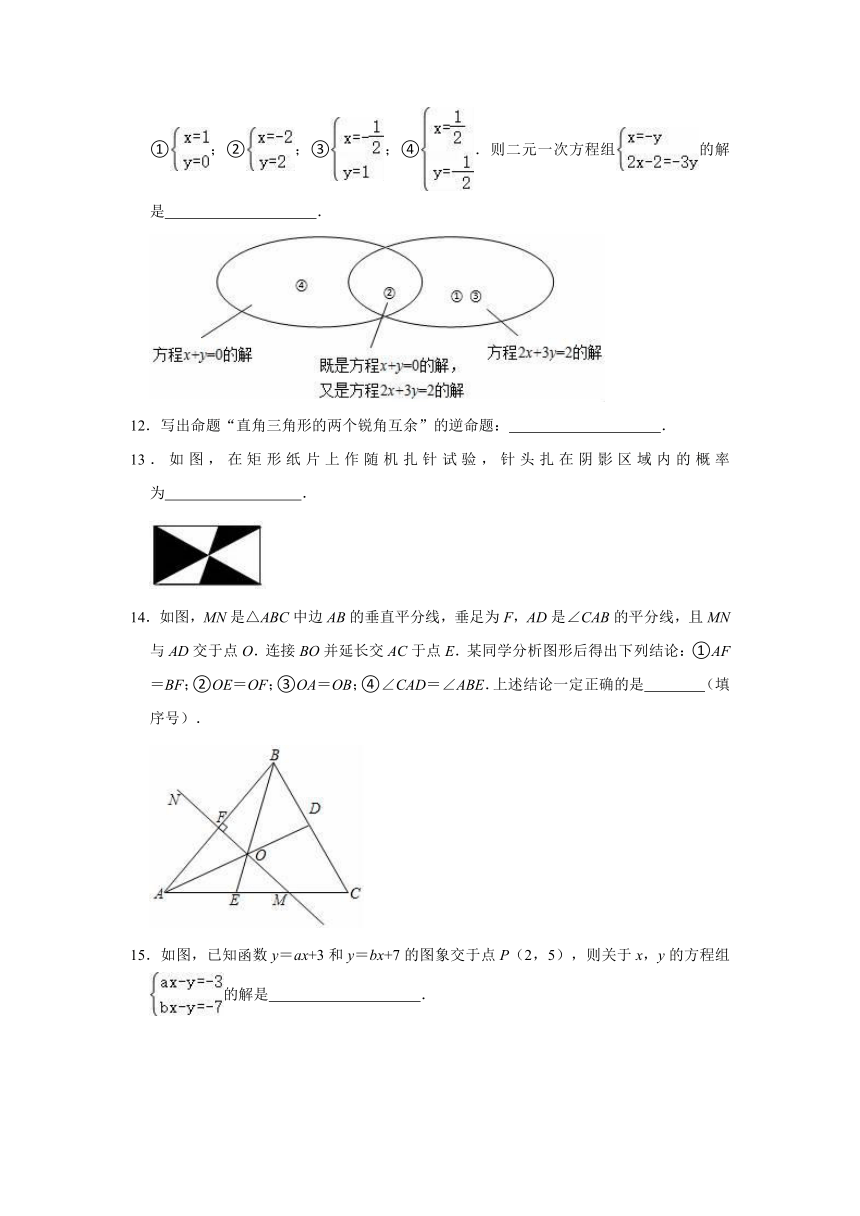
11.如图所示,下列各组数的题序已经填入图中适当的位置.
①;②;③;④.则二元一次方程组的解是
.
12.写出命题“直角三角形的两个锐角互余”的逆命题:
.
13.如图,在矩形纸片上作随机扎针试验,针头扎在阴影区域内的概率为
.
14.如图,MN是△ABC中边AB的垂直平分线,垂足为F,AD是∠CAB的平分线,且MN与AD交于点O.连接BO并延长交AC于点E.某同学分析图形后得出下列结论:①AF=BF;②OE=OF;③OA=OB;④∠CAD=∠ABE.上述结论一定正确的是
(填序号).
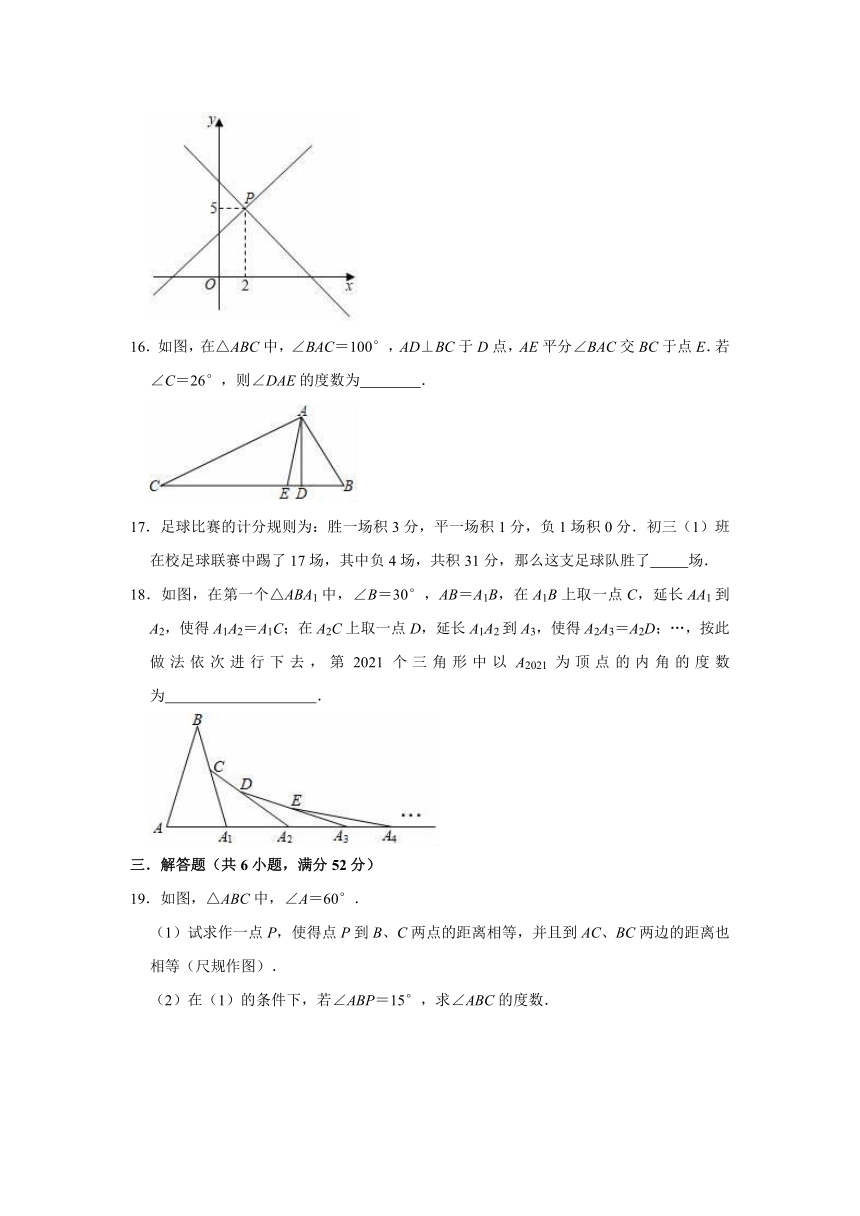
15.如图,已知函数y=ax+3和y=bx+7的图象交于点P(2,5),则关于x,y的方程组的解是
.
16.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为
.
17.足球比赛的计分规则为:胜一场积3分,平一场积1分,负1场积0分.初三(1)班在校足球联赛中踢了17场,其中负4场,共积31分,那么这支足球队胜了
场.
18.如图,在第一个△ABA1中,∠B=30°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法依次进行下去,第2021个三角形中以A2021为顶点的内角的度数为
.
三.解答题(共6小题,满分52分)
19.如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AC、BC两边的距离也相等(尺规作图).
(2)在(1)的条件下,若∠ABP=15°,求∠ABC的度数.
20.解方程组:.
21.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
22.在一个口袋中只装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”发生的概率是
;
(2)事件“从口袋中随机摸出一个球是红球”发生的概率是
;
(3)现从口袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从口袋中随机摸出一个球是白球的概率是,求取走了多少个红球?
23.∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
24.如图①,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰直角△ABC.
(1)点C的坐标为
;
(2)如图②,P是y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,若以P为直角顶点,PA为腰作等腰直角△APD,过点D作DE⊥x轴于点E,则OP﹣DE的值为
;
(3)如图③,已知点F坐标为(﹣4,﹣4),当G在y轴运动时,作等腰直角△FGH,并始终保持∠GFH=90°,FG与y轴交于点G(0,m),FH与x轴交于点H(n,0),则m与n的关系为
.
四.解答题(共1小题,满分10分,每小题10分)
25.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
(1)求∠DFE的度数;
(2)求EC的长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:解得:
,
代入y=kx﹣9得:﹣1=2k﹣9,
解得:k=4.
故选:D.
2.解:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立,不符合题意;
②如果两个实数相等,那么它们的平方相等的逆命题是如果两个实数的平方相等,那么两个实数相等,不成立,符合题意;
③如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,不成立,符合题意;
④全等三角形的对应边相等的逆命题是三条边相等的两个三角形全等,成立,不符合题意;
故选:C.
3.解:A、15个人中至少有两个人同月出生,是必然事件,符合题意;
B、一位同学在打篮球,投篮一次就投中,是随机事件,不符合题意;
C、在1,2,3,4中任取两个数,它们的和大于7是不可能事件,不符合题意;
D、掷一枚硬币,正面朝上,是随机事件,不符合题意,
故选:A.
4.解:如图,当△ABC是锐角三角形时,
∵∠B和∠C的平分线交于点I,
∴∠IBC=ABC,∠ICB=ACB,
∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=180°﹣90°+∠BAC
=90°+∠BAC,
∵∠BIC=90°+θ,
∴∠BAC=θ.
∵AB和AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠1=∠OBA,∠2=∠OCA,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC﹣∠1+∠ACB﹣∠2)
=180°﹣(180°﹣∠BAC﹣∠1﹣∠2)
=∠BAC+∠1+∠2
=2∠BAC
=2θ.
如图,当△ABC是钝角三角形时,
∠BOC=360°﹣2∠BAC=360°﹣2θ.
则∠BOC为2θ或360°﹣2θ.
故选:D.
5.解:A、A盘转出蓝色的概率为、B盘转出蓝色的概率为,此选项错误;
B、如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性不变,此选项错误;
C、由于A、B两个转盘是相互独立的,先转动A
转盘再转动B
转盘和同时转动两个转盘,游戏者配成紫色的概率相同,此选项错误;
D、画树状图如下:
由于共有6种等可能结果,而出现红色和蓝色的只有1种,
所以游戏者配成紫色的概率为,
故选:D.
6.解:设去年的收入为x元,支出为y元,由题意得:
,
故选:B.
7.解:①实数与数轴上的点一一对应,则本小题说法错误;
②过直线外一点有且只有一条直线与已知直线平行,则本小题说法错误;
③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,则本小题说法错误;
④负数没有平方根,则本小题说法正确;
故选:A.
8.解:如图,等边三角形ABC,AB=BC=4,
作AD⊥BC,垂足为D,
∴BD=CD=2,
在Rt△ABD中,AD=,
∴S△ABC=BC?AD
=×4×
=,
故选:A.
9.解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90°,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在△MQP和△NQH中,
,
∴△MQP≌△NQH(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ﹣HQ=9﹣5=4,
故选:B.
10.解:①等腰三角形的底边上的高、中线、顶角的角平分线互相重合,原命题是假命题;
②等边三角形是等腰三角形,是真命题;
③若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形,是真命题;
④等腰三角形的两个底角相等,是真命题;
⑤一腰和一腰上的高对应相等的两个等腰三角形全等,是假命题;
故选:C.
二.填空题(共8小题,满分28分)
11.解:∵两个方程的公共解即为方程组的解,
∴二元一次方程组的解是.
故答案为:.
12.解:命题“直角三角形的两个锐角互余”的逆命题为“两个锐角互余的三角形是直角三角形”.
故答案为:两个锐角互余的三角形是直角三角形.
13.解:观察发现:图中阴影部分面积=S矩形,
∴针头扎在阴影区域内的概率为;
故答案为:.
14.解:∵MN是边AB的垂直平分线,
∴AF=BF,OA=OB,
∴①③正确;
∵AD是∠CAB的平分线,
∴∠CAD=∠BAD,
∴④正确;
∵BE不一定垂直AC,
∴无法判断OE、OF是否相等,
∴②错误;
正确的有①③④,
故答案为:①③④.
15.解:方程组可变形为,
由图象可知函数y=ax+3和y=bx+7的图象交于点P(2,5),
∴关于x,y的方程组的解是,
故答案为:.
16.解:∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣26°=64°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=×100°=50°,
∴∠DAE=∠CAD﹣∠CAE=64°﹣50°=14°.
故答案为14°.
17.解:设这支足球队胜了x场,平了y场,
依题意,得:,
解得:.
故答案为:9.
18.解:∵在△ABA1中,∠B=30°,AB=A1B,
∴∠BA1A==75°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1===37.5°;
同理可得∠DA3A2=18.75°,∠EA4A3=9.375°,
∴∠An=,
∴∠A2021=.
故答案为:.
三.解答题(共6小题,满分52分)
19.解:(1)如图,点P即为所求作.
(2)设∠ACD=∠BCD=∠PBC=x,
∵∠A+∠ABC+∠ACB=180°,
∴60°+15°+3x=180°,
∴x=35°,
∴∠ABC=15°+35°=50°.
20.解:由①得,4x+3y=12③,
②+③,得5x=﹣15,
解得x=﹣3,
把x=﹣3代入②,得y=8,
∴方程组的解为.
21.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
22.解:(1)∵口袋中装有4个白球和6个红球,
∴从口袋中随机摸出一个球是绿球是不可能事件,
发生的概率为0;
故答案为:0;
(2)∵口袋中装有4个白球和6个红球,共有10个球,
∴从口袋中随机摸出一个球是红球的概率是=;
故答案为:;
(3)设取走了x个红球,根据题意得:
=,
解得:x=4,
答:取走了4个红球.
23.证明:如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,∠C=90°,
∴EC=EF,
∵EB=EC,
∴EF=BE,
又∵∠B=90°,
∴AE是∠DAB平分线.
24.解:(1)如图1,过C作CM⊥x轴于M点,
∵CM⊥OA,AC⊥AB,
∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,
∴∠MAC=∠OBA,
在△MAC和△OBA中,
,
∴△MAC≌△OBA(AAS),
∴CM=OA=2,MA=OB=4,
∴OM=6,
∴点C的坐标为(﹣6,﹣2),
故答案为(﹣6,﹣2);
(2)如图2,过D作DQ⊥OP于Q点,则四边形OEDQ是矩形,
∴DE=OQ,
∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,
∴∠QPD=∠OAP,
在△AOP和△PDQ中
,
∴△AOP≌△PDQ(AAS),
∴AO=PQ=2,
∴OP﹣DE=OP﹣OQ=PQ=OA=2,
故答案为:2;
(3)m+n=﹣8.
理由:如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,则∠HSF=∠GTF=90°=∠SOT,
∴四边形OSFT是正方形,
∴FS=FT=4,∠EFT=90°=∠HFG,
∴∠HFS=∠GFT,
在△FSH和△FTG中,
,
∴△FSH≌△FTG(AAS),
∴GT=HS,
又∵G(0,m),H(n,0),点F坐标为(﹣4,﹣4),
∴OT═OS=4,
∴GT=﹣4﹣m,HS=n﹣(﹣4)=n+4,
∴﹣4﹣m=n+4,
∴m+n=﹣8.
当点H在点S的左侧,点G在点T的上方时,
同理可得△FSH≌△FTG,
∴GT=HS,
又∵G(0,m),H(n,0),点F坐标为(﹣4,﹣4),
∴OT═OS=4,
∴GT=m﹣(﹣4)=m+4,HS=n﹣(﹣4)=﹣4﹣n,
∴﹣4﹣n=m+4,
∴m与n的关系为m+n=﹣8.
故答案为:m+n=﹣8.
四.解答题(共1小题,满分10分,每小题10分)
25.解:(1)∵△ABC≌△DEF,
∴∠D=∠A=30°,∠E=∠B=50°,
∵∠DFE+∠D+∠E=180°,
∴∠DFE=180°﹣∠D﹣∠E=180°﹣30°﹣50°=100°;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BC﹣CF=EF﹣CF,
即BF=EC,
∵BF=8,
∴EC=8.
一.选择题(共10小题,满分30分,每小题3分)
1.若二元一次方程3x﹣y=7,2x+3y=1,y=kx﹣9有公共解,则k的取值为( )
A.3
B.﹣3
C.﹣4
D.4
2.下列命题中:①同旁内角互补,两直线平行;②如果两个实数相等,那么它们的平方相等;③如果两个角是直角,那么它们相等;④全等三角形的对应边相等.逆命题不成立的是( )
A.①②
B.①②③
C.②③
D.②③④
3.下列语句中描述的事件必然发生的是( )
A.15个人中至少有两个人同月出生
B.一位同学在打篮球,投篮一次就投中
C.在1,2,3,4中任取两个数,它们的和大于7
D.掷一枚硬币,正面朝上
4.在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+θ,则∠BOC=( )
A.90°﹣θ
B.2θ
C.180°﹣θ
D.以上答案都不对
5.有两个可以自由转动的转盘,每个转盘被分成如图所示的几个扇形,游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
A.两个转盘转出蓝色的概率一样大
B.如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C.先转动A转盘再转动B转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D.游戏者配成紫色的概率为
6.小李家去年节余50000元,今年可节余95000元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为x元,支出为y元,则可列方程组为( )
A.
B.
C.
D.
7.下列命题:①有理数与数轴上的点一一对应;②过一点有且只有一条直线与已知直线平行;③从直线外一点到这条直线的垂线段叫做点到直线的距离;④负数没有平方根.其中是真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
8.已知等边三角形的边长为4,则其面积为( )平方单位.
A.4
B.8
C.12
D.16
9.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH长为( )
A.3
B.4
C.5
D.6
10.下列说法正确的有:①等腰三角形的高、中线、角平分线互相重合;②等边三角形是等腰三角形;③若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形;④等腰三角形的两个底角相等;
⑤一腰和一腰上的高对应相等的两个等腰三角形全等.其中正确的共有( )
A.5个
B.4个
C.3个
D.2个
二.填空题(共8小题,满分28分)
11.如图所示,下列各组数的题序已经填入图中适当的位置.
①;②;③;④.则二元一次方程组的解是
.
12.写出命题“直角三角形的两个锐角互余”的逆命题:
.
13.如图,在矩形纸片上作随机扎针试验,针头扎在阴影区域内的概率为
.
14.如图,MN是△ABC中边AB的垂直平分线,垂足为F,AD是∠CAB的平分线,且MN与AD交于点O.连接BO并延长交AC于点E.某同学分析图形后得出下列结论:①AF=BF;②OE=OF;③OA=OB;④∠CAD=∠ABE.上述结论一定正确的是
(填序号).
15.如图,已知函数y=ax+3和y=bx+7的图象交于点P(2,5),则关于x,y的方程组的解是
.
16.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为
.
17.足球比赛的计分规则为:胜一场积3分,平一场积1分,负1场积0分.初三(1)班在校足球联赛中踢了17场,其中负4场,共积31分,那么这支足球队胜了
场.
18.如图,在第一个△ABA1中,∠B=30°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法依次进行下去,第2021个三角形中以A2021为顶点的内角的度数为
.
三.解答题(共6小题,满分52分)
19.如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AC、BC两边的距离也相等(尺规作图).
(2)在(1)的条件下,若∠ABP=15°,求∠ABC的度数.
20.解方程组:.
21.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
22.在一个口袋中只装有4个白球和6个红球,它们除颜色外完全相同.
(1)事件“从口袋中随机摸出一个球是绿球”发生的概率是
;
(2)事件“从口袋中随机摸出一个球是红球”发生的概率是
;
(3)现从口袋中取走若干个红球,并放入相同数量的白球,充分摇匀后,要使从口袋中随机摸出一个球是白球的概率是,求取走了多少个红球?
23.∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
24.如图①,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰直角△ABC.
(1)点C的坐标为
;
(2)如图②,P是y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,若以P为直角顶点,PA为腰作等腰直角△APD,过点D作DE⊥x轴于点E,则OP﹣DE的值为
;
(3)如图③,已知点F坐标为(﹣4,﹣4),当G在y轴运动时,作等腰直角△FGH,并始终保持∠GFH=90°,FG与y轴交于点G(0,m),FH与x轴交于点H(n,0),则m与n的关系为
.
四.解答题(共1小题,满分10分,每小题10分)
25.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
(1)求∠DFE的度数;
(2)求EC的长.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:解得:
,
代入y=kx﹣9得:﹣1=2k﹣9,
解得:k=4.
故选:D.
2.解:①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立,不符合题意;
②如果两个实数相等,那么它们的平方相等的逆命题是如果两个实数的平方相等,那么两个实数相等,不成立,符合题意;
③如果两个角是直角,那么它们相等的逆命题是如果两个角相等,那么这两个角是直角,不成立,符合题意;
④全等三角形的对应边相等的逆命题是三条边相等的两个三角形全等,成立,不符合题意;
故选:C.
3.解:A、15个人中至少有两个人同月出生,是必然事件,符合题意;
B、一位同学在打篮球,投篮一次就投中,是随机事件,不符合题意;
C、在1,2,3,4中任取两个数,它们的和大于7是不可能事件,不符合题意;
D、掷一枚硬币,正面朝上,是随机事件,不符合题意,
故选:A.
4.解:如图,当△ABC是锐角三角形时,
∵∠B和∠C的平分线交于点I,
∴∠IBC=ABC,∠ICB=ACB,
∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=180°﹣90°+∠BAC
=90°+∠BAC,
∵∠BIC=90°+θ,
∴∠BAC=θ.
∵AB和AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠1=∠OBA,∠2=∠OCA,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣(∠ABC﹣∠1+∠ACB﹣∠2)
=180°﹣(180°﹣∠BAC﹣∠1﹣∠2)
=∠BAC+∠1+∠2
=2∠BAC
=2θ.
如图,当△ABC是钝角三角形时,
∠BOC=360°﹣2∠BAC=360°﹣2θ.
则∠BOC为2θ或360°﹣2θ.
故选:D.
5.解:A、A盘转出蓝色的概率为、B盘转出蓝色的概率为,此选项错误;
B、如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性不变,此选项错误;
C、由于A、B两个转盘是相互独立的,先转动A
转盘再转动B
转盘和同时转动两个转盘,游戏者配成紫色的概率相同,此选项错误;
D、画树状图如下:
由于共有6种等可能结果,而出现红色和蓝色的只有1种,
所以游戏者配成紫色的概率为,
故选:D.
6.解:设去年的收入为x元,支出为y元,由题意得:
,
故选:B.
7.解:①实数与数轴上的点一一对应,则本小题说法错误;
②过直线外一点有且只有一条直线与已知直线平行,则本小题说法错误;
③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,则本小题说法错误;
④负数没有平方根,则本小题说法正确;
故选:A.
8.解:如图,等边三角形ABC,AB=BC=4,
作AD⊥BC,垂足为D,
∴BD=CD=2,
在Rt△ABD中,AD=,
∴S△ABC=BC?AD
=×4×
=,
故选:A.
9.解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90°,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在△MQP和△NQH中,
,
∴△MQP≌△NQH(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ﹣HQ=9﹣5=4,
故选:B.
10.解:①等腰三角形的底边上的高、中线、顶角的角平分线互相重合,原命题是假命题;
②等边三角形是等腰三角形,是真命题;
③若三角形一个外角的平分线平行于三角形的一边,则这个三角形为等腰三角形,是真命题;
④等腰三角形的两个底角相等,是真命题;
⑤一腰和一腰上的高对应相等的两个等腰三角形全等,是假命题;
故选:C.
二.填空题(共8小题,满分28分)
11.解:∵两个方程的公共解即为方程组的解,
∴二元一次方程组的解是.
故答案为:.
12.解:命题“直角三角形的两个锐角互余”的逆命题为“两个锐角互余的三角形是直角三角形”.
故答案为:两个锐角互余的三角形是直角三角形.
13.解:观察发现:图中阴影部分面积=S矩形,
∴针头扎在阴影区域内的概率为;
故答案为:.
14.解:∵MN是边AB的垂直平分线,
∴AF=BF,OA=OB,
∴①③正确;
∵AD是∠CAB的平分线,
∴∠CAD=∠BAD,
∴④正确;
∵BE不一定垂直AC,
∴无法判断OE、OF是否相等,
∴②错误;
正确的有①③④,
故答案为:①③④.
15.解:方程组可变形为,
由图象可知函数y=ax+3和y=bx+7的图象交于点P(2,5),
∴关于x,y的方程组的解是,
故答案为:.
16.解:∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣26°=64°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=×100°=50°,
∴∠DAE=∠CAD﹣∠CAE=64°﹣50°=14°.
故答案为14°.
17.解:设这支足球队胜了x场,平了y场,
依题意,得:,
解得:.
故答案为:9.
18.解:∵在△ABA1中,∠B=30°,AB=A1B,
∴∠BA1A==75°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1===37.5°;
同理可得∠DA3A2=18.75°,∠EA4A3=9.375°,
∴∠An=,
∴∠A2021=.
故答案为:.
三.解答题(共6小题,满分52分)
19.解:(1)如图,点P即为所求作.
(2)设∠ACD=∠BCD=∠PBC=x,
∵∠A+∠ABC+∠ACB=180°,
∴60°+15°+3x=180°,
∴x=35°,
∴∠ABC=15°+35°=50°.
20.解:由①得,4x+3y=12③,
②+③,得5x=﹣15,
解得x=﹣3,
把x=﹣3代入②,得y=8,
∴方程组的解为.
21.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
22.解:(1)∵口袋中装有4个白球和6个红球,
∴从口袋中随机摸出一个球是绿球是不可能事件,
发生的概率为0;
故答案为:0;
(2)∵口袋中装有4个白球和6个红球,共有10个球,
∴从口袋中随机摸出一个球是红球的概率是=;
故答案为:;
(3)设取走了x个红球,根据题意得:
=,
解得:x=4,
答:取走了4个红球.
23.证明:如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,∠C=90°,
∴EC=EF,
∵EB=EC,
∴EF=BE,
又∵∠B=90°,
∴AE是∠DAB平分线.
24.解:(1)如图1,过C作CM⊥x轴于M点,
∵CM⊥OA,AC⊥AB,
∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,
∴∠MAC=∠OBA,
在△MAC和△OBA中,
,
∴△MAC≌△OBA(AAS),
∴CM=OA=2,MA=OB=4,
∴OM=6,
∴点C的坐标为(﹣6,﹣2),
故答案为(﹣6,﹣2);
(2)如图2,过D作DQ⊥OP于Q点,则四边形OEDQ是矩形,
∴DE=OQ,
∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,
∴∠QPD=∠OAP,
在△AOP和△PDQ中
,
∴△AOP≌△PDQ(AAS),
∴AO=PQ=2,
∴OP﹣DE=OP﹣OQ=PQ=OA=2,
故答案为:2;
(3)m+n=﹣8.
理由:如图3,过点F分别作FS⊥x轴于S点,FT⊥y轴于T点,则∠HSF=∠GTF=90°=∠SOT,
∴四边形OSFT是正方形,
∴FS=FT=4,∠EFT=90°=∠HFG,
∴∠HFS=∠GFT,
在△FSH和△FTG中,
,
∴△FSH≌△FTG(AAS),
∴GT=HS,
又∵G(0,m),H(n,0),点F坐标为(﹣4,﹣4),
∴OT═OS=4,
∴GT=﹣4﹣m,HS=n﹣(﹣4)=n+4,
∴﹣4﹣m=n+4,
∴m+n=﹣8.
当点H在点S的左侧,点G在点T的上方时,
同理可得△FSH≌△FTG,
∴GT=HS,
又∵G(0,m),H(n,0),点F坐标为(﹣4,﹣4),
∴OT═OS=4,
∴GT=m﹣(﹣4)=m+4,HS=n﹣(﹣4)=﹣4﹣n,
∴﹣4﹣n=m+4,
∴m与n的关系为m+n=﹣8.
故答案为:m+n=﹣8.
四.解答题(共1小题,满分10分,每小题10分)
25.解:(1)∵△ABC≌△DEF,
∴∠D=∠A=30°,∠E=∠B=50°,
∵∠DFE+∠D+∠E=180°,
∴∠DFE=180°﹣∠D﹣∠E=180°﹣30°﹣50°=100°;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BC﹣CF=EF﹣CF,
即BF=EC,
∵BF=8,
∴EC=8.
同课章节目录
