2020-2021学年人教五四新版六年级下册数学期末冲刺试题(word版含解析)
文档属性
| 名称 | 2020-2021学年人教五四新版六年级下册数学期末冲刺试题(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 00:00:00 | ||
图片预览




文档简介
2020-2021学年人教五四新版六年级下册数学期末冲刺试题
一.选择题(共10小题,满分30分,每小题3分)
1.﹣3的相反数是( )
A.﹣3
B.3
C.
D.
2.随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元.将数据“2684亿”用科学记数法表示( )
A.2.684×103
B.2.684×1011
C.2.684×1012
D.2.684×107
3.在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离校情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A.1个
B.2个
C.3个
D.4个
4.如图,A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是( )
A.经过一点可以作无数条直线
B.经过两点有且只有一条直线
C.两点之间,有若干种连接方式
D.两点之间,线段最短
5.如图所示几何体的左视图正确的是( )
A.
B.
C.
D.
6.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
7.下列平面图形经过折叠不能围成一个正方体的是( )
A.
B.
C.
D.
8.北京市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,某社区实行垃圾分类积分兑换奖品活动.随机抽取了若干户5月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分x/分
频数
频率
0≤x<50
4
0.1
50≤x<100
8
0.2
100≤x<200
16
b
x≥200
a
0.3
根据以上信息可得( )
A.a=40,b=0.4
B.a=12,b=0.4
C.a=10,b=0.5
D.a=4,b=0.5
9.四位同学画数轴如图所示,你认为正确的是( )
A.
B.
C.
D.
10.已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有( )
①AP=BP;
②BP=AB;
③AB=2AP;
④AP+PB=AB.
A.1个
B.2个
C.3个
D.4个
二.填空题(共10小题,满分30分,每小题3分)
11.比0小3的数是
.
12.如果体重增加1.5kg记作+1.5kg,那么体重减少2kg记作
kg.
13.比较大小:﹣
﹣.
14.单项式x3的次数是
.
15.一个角的余角比它的补角的还少40°,则这个角的度数为
度.
16.为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是
.
17.如图,某市有三个中学A,B,O.中学A在中学O的北偏东61°15′的方向上,中学B在中学O的南偏东39°45′的方向上,则∠AOB的度数是
.
18.一个数x的与3的差,用代数式表示为
.
19.如图,这是用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成…按照这样的规律排列下去,则第6个图案中共有
个白子.
20.已知线段AB=10cm,直线AB上有一点C,且BC=4cm,M是线段BC的中点,则AM的长是
cm.
三.解答题(共7小题,满分60分)
21.如图,已知直线l和直线外三点A,B,C,按下列要求画图,填空:
(1)画射线AB;
(2)连接BC;
(3)延长CB至D,使得BD=BC;
(4)在直线上确定点E,使得AE+CE最小,请写出你作图的依据
.
22.计算:
(1)|﹣|÷(﹣)﹣×(﹣2)3;
(2)(﹣+)÷(﹣).
23.先化简,再求值:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)的值,其中x=1,y=﹣2.
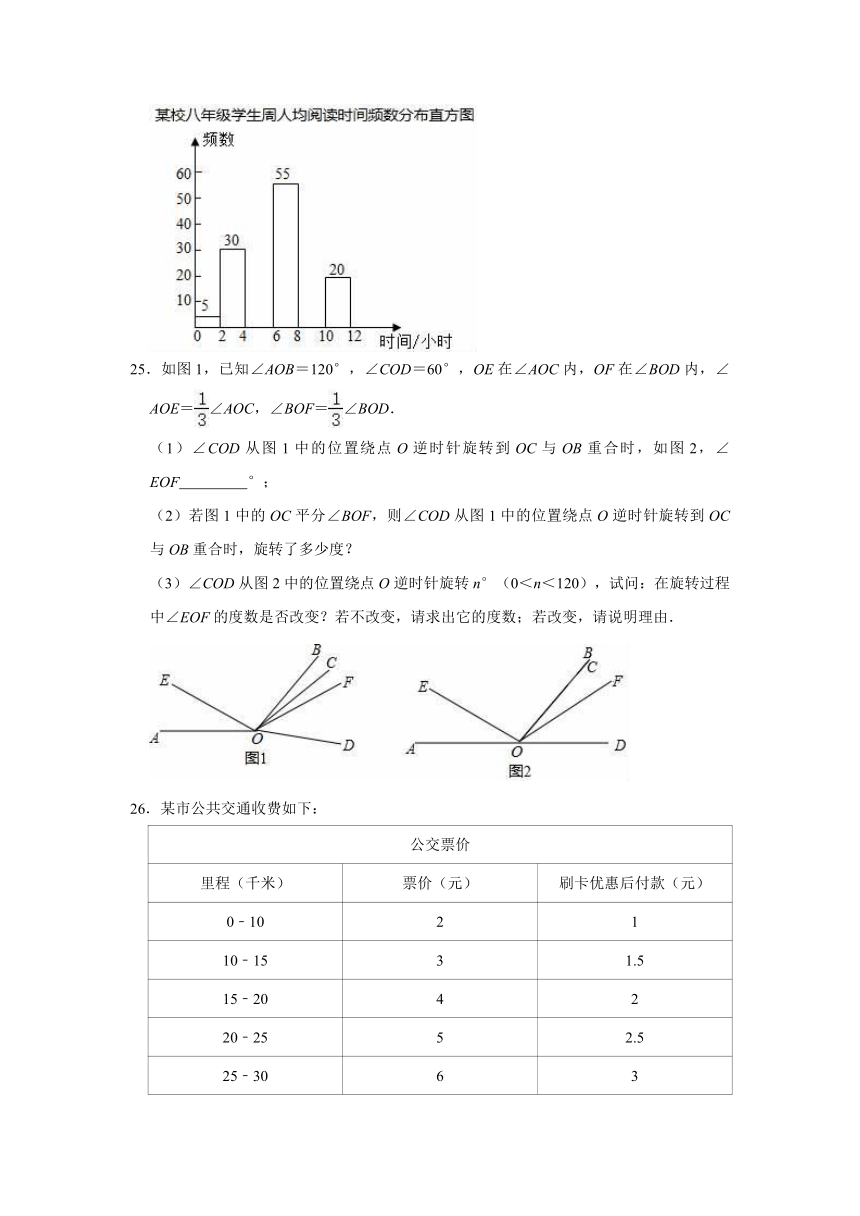
24.为了进一步推进“书香房山”建设,2020年4月房山区启动2020年“书香中国?北京阅读季”全民阅读活动.在一个月的活动中随机调查了某校八年级学生的周人均阅读时间的情况,整理并绘制了如下的统计图表:
某校八年级学生周人均阅读时间频数分布表
周人均阅读时间x(小时)
频数
频率
0≤x<2
5
0.025
2≤x<4
30
0.150
4≤x<6
a
0.200
6≤x<8
55
0.275
8≤x<10
50
0.250
10≤x<12
20
b
合计
200
1.000
请根据以上信息,解答下列问题:
(1)在频数分布表中a=
,b=
;
(2)补全频数分布直方图;
(3)若该校有1000名学生,根据调查数据,请你估计该校学生周人均阅读时间不少于6小时的学生大约有
人.
25.如图1,已知∠AOB=120°,∠COD=60°,OE在∠AOC内,OF在∠BOD内,∠AOE=∠AOC,∠BOF=∠BOD.
(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,∠EOF
°;
(2)若图1中的OC平分∠BOF,则∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,旋转了多少度?
(3)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120),试问:在旋转过程中∠EOF的度数是否改变?若不改变,请求出它的度数;若改变,请说明理由.
26.某市公共交通收费如下:
公交票价
里程(千米)
票价(元)
刷卡优惠后付款(元)
0﹣10
2
1
10﹣15
3
1.5
15﹣20
4
2
20﹣25
5
2.5
25﹣30
6
3
以后每增加5千米
增加1元
增加0.5元
地铁票价
里程(千米)
票价(元)
0﹣6
3
6﹣12
4
12﹣22
5
22﹣32
6
32﹣52
7
52﹣72
8
以后每增加20千米
增加1元
(公交票价10千米(含)内2元,不足10千米按10千米计算,其他里程类同;地铁票价6千米(含)内3元,不足6千米按6千米计算,其他里程类同)
(1)张阿姨周日去看望父母,可是张阿姨忘了带一卡通,请你帮助张阿姨思考两个问题:
①若到父母家无论乘公交车还是地铁距离都是24千米,选择哪种公交交通工具费用较少?
②若只用10元钱乘坐公交或地铁,选择哪种公共交通工具乘坐的里程更远?
(2)张阿姨下周日计划使用一卡通刷卡乘公共交通到景点游玩,若里程小于120千米,公交、地铁均可直达.请问:选择公交还是选择地铁出行更省钱?为什么?
27.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是c,且|a+8|与(c﹣16)2互为相反数.(忽略两辆火车的车身及双铁轨的宽度.)
(1)求此时刻快车头A与慢车头C之间相距
单位长度.
(2)从此时刻开始,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,再行驶
秒两列火车的车头A、C相距8个单位长度.
(3)在(2)中快车、慢车速度不变的情况下,此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟内,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).则这段时间t是
秒,定值是
单位长度.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:﹣3的相反数是3.
故选:B.
2.解:将2684亿=268400000000用科学记数法表示为:2.684×1011.
故选:B.
3.解:①了解学校口罩、洗手液、消毒片的储备情况适合普查;
②了解全体师生在寒假期间的离锡情况适合普查;
③了解全体师生入校时的体温情况适合普查;
④了解全体师生对“七步洗手法”的运用情况适合抽样调查.
故选:C.
4.解:A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是两点之间,线段最短,
故选:D.
5.解:从几何体的左面看所得到的图形是:
故选:A.
6.解:A、单项式xy2的系数是,原说法错误,故此选项不符合题意;
B、单项式﹣5x2的次数为2,原说法错误,故此选项不符合题意;
C、多项式x2+2x+18是二次三项式,原说法正确,故此选项符合题意;
D、多项式x2+y2﹣1的常数项是﹣1,原说法错误,故此选项不符合题意,
故选:C.
7.解:A,B,D经过折叠均能围成正方体,C、折叠后有两个面重合,不能折成正方体.
故选:C.
8.解:a=×0.3=12,b=16÷=04;
故选:B.
9.解:A中,无原点;
B中,无正方向;
D中,数的顺序错了.
故选:C.
10.解:如图所示:
①∵AP=BP,∴点P是线段AB的中点,故本小题正确;
②点P可能在AB的延长线上时不成立,故本小题错误;
③P可能在BA的延长线上时不成立,故本小题错误;
④∵AP+PB=AB,∴点P在线段AB上,不能说明点P是中点,故本小题错误.
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:比0小3的数是0﹣3=﹣3,
故答案为:﹣3.
12.解:如果体重增加1.5kg记作+1.5kg,那么体重减少2kg记作﹣2kg.
故答案为:﹣2.
13.解:|﹣|=,|﹣|=,
∵>,
∴﹣<﹣.
故答案为:<.
14.解:单项式x3的次数是3,
故答案为:3.
15.解:设这个角是α,
根据题意可得:90°﹣α=(180°﹣α)﹣40°,
解可得α=30°
16.解:为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是2000.
故答案为:2000.
17.解:∠AOB=180°﹣61°15′﹣39°45′=79°,
故答案为:79°.
18.解:一个数x的与3的差,用代数式表示为x﹣3,
故答案为:
x﹣3.
19.解:第1个图案由1个黑子组成,
第2个图案由1个黑子和6个白子组成,
第3个图案由1+3×6﹣6=13个黑子和6个白子组成,
第4个图案由13个黑子和6+4×6﹣6=24个白子组成,
第5个图案由13+5×6﹣6=37个黑子和24个白子组成,
第6个图案由37个黑子和24+6×6﹣6=54个白子组成.
故答案为54.
20.解:①如图1所示,当点C在点A与B之间时,
∵线段AB=10cm,BC=4cm,
∴AC=10﹣4=6cm.
∵M是线段BC的中点,
∴CM=BC=2cm,
∴AM=AC+CM=6+2=8cm;
②当点C在点B的右侧时,
∵BC=4cm,M是线段BC的中点,
∴BM=BC=2cm,
∴AM=AB+BM=10+2=12cm.
综上所述,线段AM的长为8cm或12cm.
故答案为:8或12.
三.解答题(共7小题,满分60分)
21.解:(1)射线AB如图所示.
(2)线段BC如图所示.
(3)线段BD如图所示.
(4)连接AC交直线l于点E,此时AE+EC的值最小.理由:两点之间线段最短.
故答案为两点之间线段最短.
22.解:(1)|﹣|÷(﹣)﹣×(﹣2)3
=÷(﹣)﹣×(﹣8)
=﹣2+1
=﹣1.
(2)(﹣+)÷(﹣)
=×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+18﹣4
=﹣2.
23.解:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)
=3y2﹣x2+4x2﹣6xy﹣3x2﹣3y2
=﹣6xy
当x=1,y=﹣2时,原式=﹣6×1×(﹣2)=12.
24.解:(1)a=200﹣5﹣30﹣55﹣50﹣20=40(人),b=1.000﹣0.250﹣0.275﹣0.200﹣0.150﹣0.025=0.100,
故答案为:40,0.100;
(2)补全频数分布直方图,如图所示:
(3)1000×(0.100+0.250+0.275)=625(人),
故答案为:625.
25.解:(1)由题意;∠EOF=∠AOB+∠COD=80°+20°=100°;
故答案为:=100.
(2)∵OC平分∠BOF,
∴∠BOC=∠COF,
设∠BOC=x°,
则∠BOF=2x°,∠BOD=(x+60)°,
由∠BOF=∠BOD,
得:2x°=(x+60)°,
解得:x=12,
∴∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,旋转了12度;
(3)不改变
①当0<n<60时,如图a,
∠AOC=(120﹣n)°,∠BOD=(60﹣n)°,
∵∠AOE=∠AOC,∠BOF=∠BOD,
∴∠EOF=∠EOC+∠COB+∠BOF
=
=
=100°;
②n=60时,如图b,
此时OD,OF与OB重合,
此时,∠EOF=100°;
③当60<n<120时,如图c,
∠AOC=(120﹣n)°,∠BOD=(60﹣n)°,
∠EOF=∠EOC+∠COD+∠DOF
=
=
=100°;
综上,在∠COD旋转过程中,∠EOF的度数不改变,始终等于100°.
26.解:(1)①由表格中的数据可得,
乘坐公交车行驶24千米,需要车票为5元,乘坐地铁需要6元,
因此选择乘坐公交车费用较少;
②乘坐公交车行驶路程为:(10﹣2)×5+10=50千米,
乘坐地铁行驶的路程为:(10﹣6)×20+32=112千米,
因此乘坐地铁行驶路程较远;
(2)根据表格中数据变化可得,行驶路程x千米,
x≤85时,公交省钱;
当85<x≤90时,公交费(9元)=地铁费(9元),费用一样;
当90<x≤92时,公交费(9.5元)<地铁费(9元),地铁省钱;
当92<x≤95时,公交费(9.5元)<地铁费(10元),公交省钱;
当95<x≤100时,公交费(10元)=地铁费(10元),费用一样;
当100<x≤120时,地铁省钱.
27.解:(1)∵|a+8|与(b﹣16)2互为相反数,
∴|a+8|+(b﹣16)2=0,
∴a+8=0,b﹣16=0,
解得a=﹣8,b=16.
∴此时刻快车头A与慢车头C之间相距16﹣(﹣8)=24单位长度;
故答案为:24;
(2)(24﹣8)÷(6+2)
=16÷8
=2(秒).
或(24+8)÷(6+2)=4(秒)
答:再行驶2秒或4秒两列火车行驶到车头AC相距8个单位长度;
故答案为:2或4;
(3)∵PA+PB=AB=2,
当P在CD之间时,PC+PD是定值4,
t=4÷(6+2)
=4÷8
=0.5(秒),
此时PA+PC+PB+PD=(PA+PB)+(PC+PD)=2+4=6(单位长度).
故这个时间是0.5秒,定值是6单位长度.
故答案为:0.5,6.
一.选择题(共10小题,满分30分,每小题3分)
1.﹣3的相反数是( )
A.﹣3
B.3
C.
D.
2.随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元.将数据“2684亿”用科学记数法表示( )
A.2.684×103
B.2.684×1011
C.2.684×1012
D.2.684×107
3.在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离校情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A.1个
B.2个
C.3个
D.4个
4.如图,A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是( )
A.经过一点可以作无数条直线
B.经过两点有且只有一条直线
C.两点之间,有若干种连接方式
D.两点之间,线段最短
5.如图所示几何体的左视图正确的是( )
A.
B.
C.
D.
6.下列说法中,正确的是( )
A.单项式xy2的系数是x
B.单项式﹣5x2的次数为﹣5
C.多项式x2+2x+18是二次三项式
D.多项式x2+y2﹣1的常数项是1
7.下列平面图形经过折叠不能围成一个正方体的是( )
A.
B.
C.
D.
8.北京市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,某社区实行垃圾分类积分兑换奖品活动.随机抽取了若干户5月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分x/分
频数
频率
0≤x<50
4
0.1
50≤x<100
8
0.2
100≤x<200
16
b
x≥200
a
0.3
根据以上信息可得( )
A.a=40,b=0.4
B.a=12,b=0.4
C.a=10,b=0.5
D.a=4,b=0.5
9.四位同学画数轴如图所示,你认为正确的是( )
A.
B.
C.
D.
10.已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有( )
①AP=BP;
②BP=AB;
③AB=2AP;
④AP+PB=AB.
A.1个
B.2个
C.3个
D.4个
二.填空题(共10小题,满分30分,每小题3分)
11.比0小3的数是
.
12.如果体重增加1.5kg记作+1.5kg,那么体重减少2kg记作
kg.
13.比较大小:﹣
﹣.
14.单项式x3的次数是
.
15.一个角的余角比它的补角的还少40°,则这个角的度数为
度.
16.为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是
.
17.如图,某市有三个中学A,B,O.中学A在中学O的北偏东61°15′的方向上,中学B在中学O的南偏东39°45′的方向上,则∠AOB的度数是
.
18.一个数x的与3的差,用代数式表示为
.
19.如图,这是用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成…按照这样的规律排列下去,则第6个图案中共有
个白子.
20.已知线段AB=10cm,直线AB上有一点C,且BC=4cm,M是线段BC的中点,则AM的长是
cm.
三.解答题(共7小题,满分60分)
21.如图,已知直线l和直线外三点A,B,C,按下列要求画图,填空:
(1)画射线AB;
(2)连接BC;
(3)延长CB至D,使得BD=BC;
(4)在直线上确定点E,使得AE+CE最小,请写出你作图的依据
.
22.计算:
(1)|﹣|÷(﹣)﹣×(﹣2)3;
(2)(﹣+)÷(﹣).
23.先化简,再求值:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)的值,其中x=1,y=﹣2.
24.为了进一步推进“书香房山”建设,2020年4月房山区启动2020年“书香中国?北京阅读季”全民阅读活动.在一个月的活动中随机调查了某校八年级学生的周人均阅读时间的情况,整理并绘制了如下的统计图表:
某校八年级学生周人均阅读时间频数分布表
周人均阅读时间x(小时)
频数
频率
0≤x<2
5
0.025
2≤x<4
30
0.150
4≤x<6
a
0.200
6≤x<8
55
0.275
8≤x<10
50
0.250
10≤x<12
20
b
合计
200
1.000
请根据以上信息,解答下列问题:
(1)在频数分布表中a=
,b=
;
(2)补全频数分布直方图;
(3)若该校有1000名学生,根据调查数据,请你估计该校学生周人均阅读时间不少于6小时的学生大约有
人.
25.如图1,已知∠AOB=120°,∠COD=60°,OE在∠AOC内,OF在∠BOD内,∠AOE=∠AOC,∠BOF=∠BOD.
(1)∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,如图2,∠EOF
°;
(2)若图1中的OC平分∠BOF,则∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,旋转了多少度?
(3)∠COD从图2中的位置绕点O逆时针旋转n°(0<n<120),试问:在旋转过程中∠EOF的度数是否改变?若不改变,请求出它的度数;若改变,请说明理由.
26.某市公共交通收费如下:
公交票价
里程(千米)
票价(元)
刷卡优惠后付款(元)
0﹣10
2
1
10﹣15
3
1.5
15﹣20
4
2
20﹣25
5
2.5
25﹣30
6
3
以后每增加5千米
增加1元
增加0.5元
地铁票价
里程(千米)
票价(元)
0﹣6
3
6﹣12
4
12﹣22
5
22﹣32
6
32﹣52
7
52﹣72
8
以后每增加20千米
增加1元
(公交票价10千米(含)内2元,不足10千米按10千米计算,其他里程类同;地铁票价6千米(含)内3元,不足6千米按6千米计算,其他里程类同)
(1)张阿姨周日去看望父母,可是张阿姨忘了带一卡通,请你帮助张阿姨思考两个问题:
①若到父母家无论乘公交车还是地铁距离都是24千米,选择哪种公交交通工具费用较少?
②若只用10元钱乘坐公交或地铁,选择哪种公共交通工具乘坐的里程更远?
(2)张阿姨下周日计划使用一卡通刷卡乘公共交通到景点游玩,若里程小于120千米,公交、地铁均可直达.请问:选择公交还是选择地铁出行更省钱?为什么?
27.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是c,且|a+8|与(c﹣16)2互为相反数.(忽略两辆火车的车身及双铁轨的宽度.)
(1)求此时刻快车头A与慢车头C之间相距
单位长度.
(2)从此时刻开始,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,再行驶
秒两列火车的车头A、C相距8个单位长度.
(3)在(2)中快车、慢车速度不变的情况下,此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟内,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).则这段时间t是
秒,定值是
单位长度.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:﹣3的相反数是3.
故选:B.
2.解:将2684亿=268400000000用科学记数法表示为:2.684×1011.
故选:B.
3.解:①了解学校口罩、洗手液、消毒片的储备情况适合普查;
②了解全体师生在寒假期间的离锡情况适合普查;
③了解全体师生入校时的体温情况适合普查;
④了解全体师生对“七步洗手法”的运用情况适合抽样调查.
故选:C.
4.解:A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是两点之间,线段最短,
故选:D.
5.解:从几何体的左面看所得到的图形是:
故选:A.
6.解:A、单项式xy2的系数是,原说法错误,故此选项不符合题意;
B、单项式﹣5x2的次数为2,原说法错误,故此选项不符合题意;
C、多项式x2+2x+18是二次三项式,原说法正确,故此选项符合题意;
D、多项式x2+y2﹣1的常数项是﹣1,原说法错误,故此选项不符合题意,
故选:C.
7.解:A,B,D经过折叠均能围成正方体,C、折叠后有两个面重合,不能折成正方体.
故选:C.
8.解:a=×0.3=12,b=16÷=04;
故选:B.
9.解:A中,无原点;
B中,无正方向;
D中,数的顺序错了.
故选:C.
10.解:如图所示:
①∵AP=BP,∴点P是线段AB的中点,故本小题正确;
②点P可能在AB的延长线上时不成立,故本小题错误;
③P可能在BA的延长线上时不成立,故本小题错误;
④∵AP+PB=AB,∴点P在线段AB上,不能说明点P是中点,故本小题错误.
故选:A.
二.填空题(共10小题,满分30分,每小题3分)
11.解:比0小3的数是0﹣3=﹣3,
故答案为:﹣3.
12.解:如果体重增加1.5kg记作+1.5kg,那么体重减少2kg记作﹣2kg.
故答案为:﹣2.
13.解:|﹣|=,|﹣|=,
∵>,
∴﹣<﹣.
故答案为:<.
14.解:单项式x3的次数是3,
故答案为:3.
15.解:设这个角是α,
根据题意可得:90°﹣α=(180°﹣α)﹣40°,
解可得α=30°
16.解:为了解无锡市八年级学生的身高情况,从中任意抽取2000名学生的身高进行统计,在这个问题中,样本容量是2000.
故答案为:2000.
17.解:∠AOB=180°﹣61°15′﹣39°45′=79°,
故答案为:79°.
18.解:一个数x的与3的差,用代数式表示为x﹣3,
故答案为:
x﹣3.
19.解:第1个图案由1个黑子组成,
第2个图案由1个黑子和6个白子组成,
第3个图案由1+3×6﹣6=13个黑子和6个白子组成,
第4个图案由13个黑子和6+4×6﹣6=24个白子组成,
第5个图案由13+5×6﹣6=37个黑子和24个白子组成,
第6个图案由37个黑子和24+6×6﹣6=54个白子组成.
故答案为54.
20.解:①如图1所示,当点C在点A与B之间时,
∵线段AB=10cm,BC=4cm,
∴AC=10﹣4=6cm.
∵M是线段BC的中点,
∴CM=BC=2cm,
∴AM=AC+CM=6+2=8cm;
②当点C在点B的右侧时,
∵BC=4cm,M是线段BC的中点,
∴BM=BC=2cm,
∴AM=AB+BM=10+2=12cm.
综上所述,线段AM的长为8cm或12cm.
故答案为:8或12.
三.解答题(共7小题,满分60分)
21.解:(1)射线AB如图所示.
(2)线段BC如图所示.
(3)线段BD如图所示.
(4)连接AC交直线l于点E,此时AE+EC的值最小.理由:两点之间线段最短.
故答案为两点之间线段最短.
22.解:(1)|﹣|÷(﹣)﹣×(﹣2)3
=÷(﹣)﹣×(﹣8)
=﹣2+1
=﹣1.
(2)(﹣+)÷(﹣)
=×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+18﹣4
=﹣2.
23.解:3y2﹣x2+2(2x2﹣3xy)﹣3(x2+y2)
=3y2﹣x2+4x2﹣6xy﹣3x2﹣3y2
=﹣6xy
当x=1,y=﹣2时,原式=﹣6×1×(﹣2)=12.
24.解:(1)a=200﹣5﹣30﹣55﹣50﹣20=40(人),b=1.000﹣0.250﹣0.275﹣0.200﹣0.150﹣0.025=0.100,
故答案为:40,0.100;
(2)补全频数分布直方图,如图所示:
(3)1000×(0.100+0.250+0.275)=625(人),
故答案为:625.
25.解:(1)由题意;∠EOF=∠AOB+∠COD=80°+20°=100°;
故答案为:=100.
(2)∵OC平分∠BOF,
∴∠BOC=∠COF,
设∠BOC=x°,
则∠BOF=2x°,∠BOD=(x+60)°,
由∠BOF=∠BOD,
得:2x°=(x+60)°,
解得:x=12,
∴∠COD从图1中的位置绕点O逆时针旋转到OC与OB重合时,旋转了12度;
(3)不改变
①当0<n<60时,如图a,
∠AOC=(120﹣n)°,∠BOD=(60﹣n)°,
∵∠AOE=∠AOC,∠BOF=∠BOD,
∴∠EOF=∠EOC+∠COB+∠BOF
=
=
=100°;
②n=60时,如图b,
此时OD,OF与OB重合,
此时,∠EOF=100°;
③当60<n<120时,如图c,
∠AOC=(120﹣n)°,∠BOD=(60﹣n)°,
∠EOF=∠EOC+∠COD+∠DOF
=
=
=100°;
综上,在∠COD旋转过程中,∠EOF的度数不改变,始终等于100°.
26.解:(1)①由表格中的数据可得,
乘坐公交车行驶24千米,需要车票为5元,乘坐地铁需要6元,
因此选择乘坐公交车费用较少;
②乘坐公交车行驶路程为:(10﹣2)×5+10=50千米,
乘坐地铁行驶的路程为:(10﹣6)×20+32=112千米,
因此乘坐地铁行驶路程较远;
(2)根据表格中数据变化可得,行驶路程x千米,
x≤85时,公交省钱;
当85<x≤90时,公交费(9元)=地铁费(9元),费用一样;
当90<x≤92时,公交费(9.5元)<地铁费(9元),地铁省钱;
当92<x≤95时,公交费(9.5元)<地铁费(10元),公交省钱;
当95<x≤100时,公交费(10元)=地铁费(10元),费用一样;
当100<x≤120时,地铁省钱.
27.解:(1)∵|a+8|与(b﹣16)2互为相反数,
∴|a+8|+(b﹣16)2=0,
∴a+8=0,b﹣16=0,
解得a=﹣8,b=16.
∴此时刻快车头A与慢车头C之间相距16﹣(﹣8)=24单位长度;
故答案为:24;
(2)(24﹣8)÷(6+2)
=16÷8
=2(秒).
或(24+8)÷(6+2)=4(秒)
答:再行驶2秒或4秒两列火车行驶到车头AC相距8个单位长度;
故答案为:2或4;
(3)∵PA+PB=AB=2,
当P在CD之间时,PC+PD是定值4,
t=4÷(6+2)
=4÷8
=0.5(秒),
此时PA+PC+PB+PD=(PA+PB)+(PC+PD)=2+4=6(单位长度).
故这个时间是0.5秒,定值是6单位长度.
故答案为:0.5,6.
同课章节目录
