2020-2021学年北师大版九年级数学下册第三章 3.1-3.2 同步练习题(Word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册第三章 3.1-3.2 同步练习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 200.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 09:18:42 | ||
图片预览

文档简介
2020-2021学年北师大版九年级数学下册第三章
3.1-3.2
同步练习题
一、选择题
1、已知⊙O与点P在同一平面内,若⊙O的半径为5,线段OP的长为4,则点P(
)
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.在⊙O上或在⊙O内
2、下列说法错误的是(
)
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆叫做等圆
3、下列说法正确的是(
)
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的圆心角相等
4、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(
)
A.32°
B.60°
C.68°
D.64°
5、如图,在⊙O中,=2,则以下数量关系正确的是(
)
A.AB=AC
B.AC=2AB
C.AC<2AB
D.AC>2AB
6、如图,已知=,则AB与CD的关系为(
)
A.AB=CD
B.AB>CD
C.ABD.不能确定
7、如图,在矩形ABCD中,AB=8,BC=3,点P在边AB上,且BP=3AP.如果⊙P是以点P为圆心、PD为半径的圆,那么下列判断正确的是(
)
A.点B,C均在⊙P外
B.点B在⊙P外,点C在⊙P内
C.点B在⊙P内,点C在⊙P外
D.点B,C均在⊙P内
二、填空题
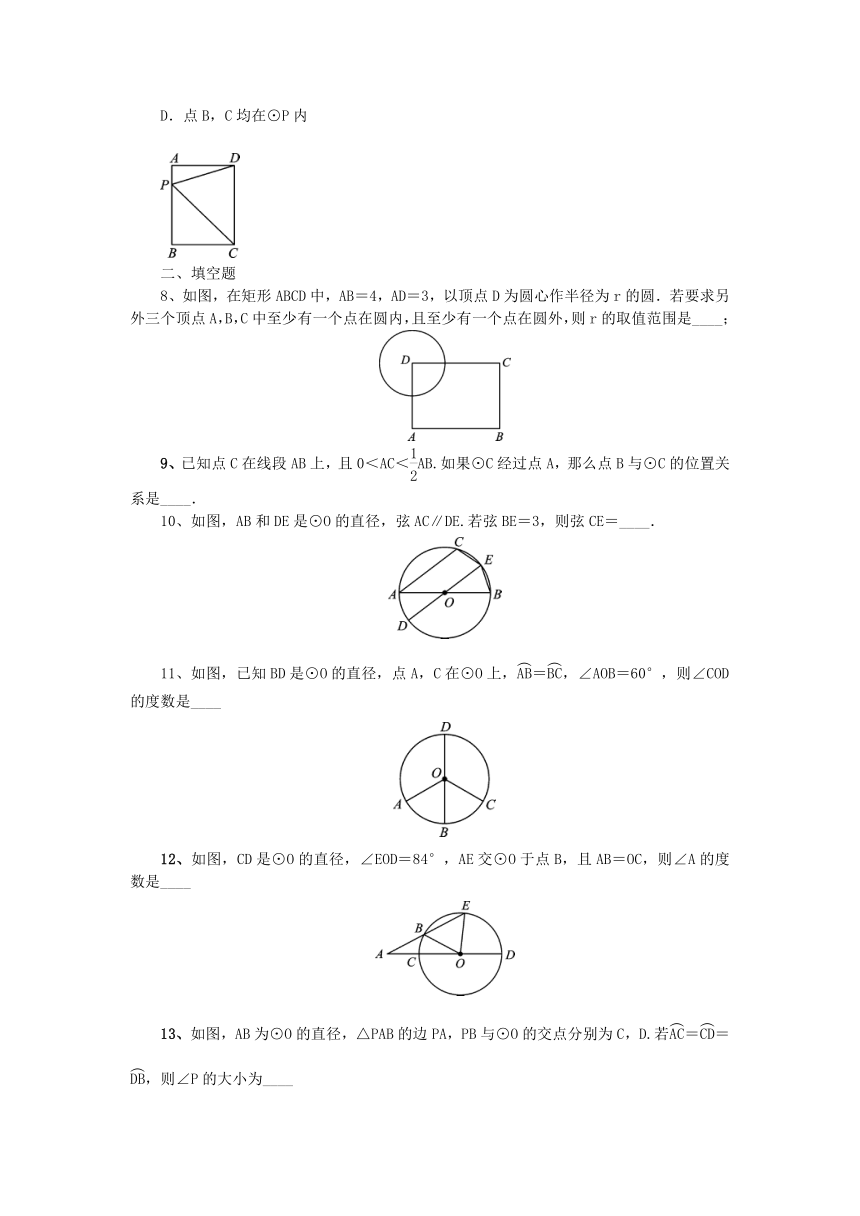
8、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是____;
9、已知点C在线段AB上,且0<AC<AB.如果⊙C经过点A,那么点B与⊙C的位置关系是____.
10、如图,AB和DE是⊙O的直径,弦AC∥DE.若弦BE=3,则弦CE=____.
11、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是____
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是____
13、如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C,D.若==,则∠P的大小为____
三、解答题
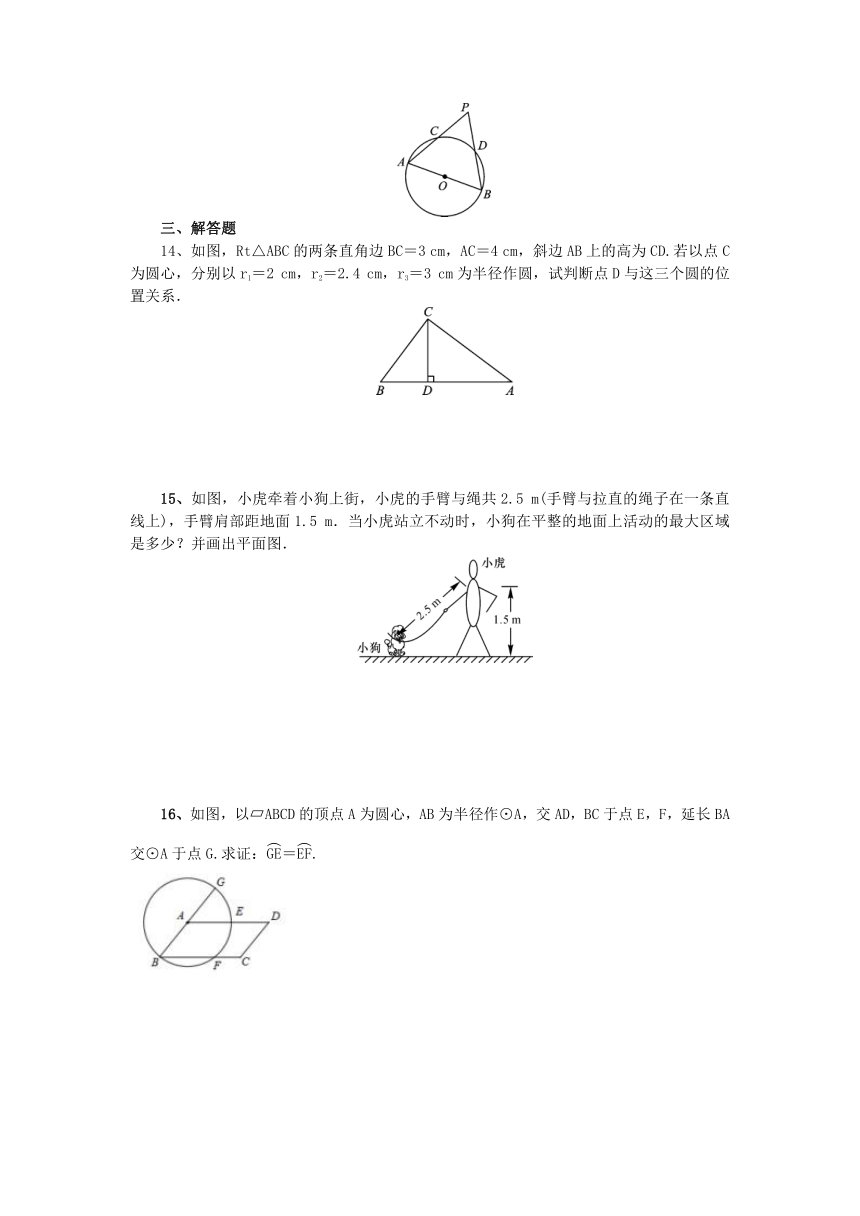
14、如图,Rt△ABC的两条直角边BC=3
cm,AC=4
cm,斜边AB上的高为CD.若以点C为圆心,分别以r1=2
cm,r2=2.4
cm,r3=3
cm为半径作圆,试判断点D与这三个圆的位置关系.
15、如图,小虎牵着小狗上街,小虎的手臂与绳共2.5
m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
16、如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,交AD,BC于点E,F,延长BA交⊙A于点G.求证:=.
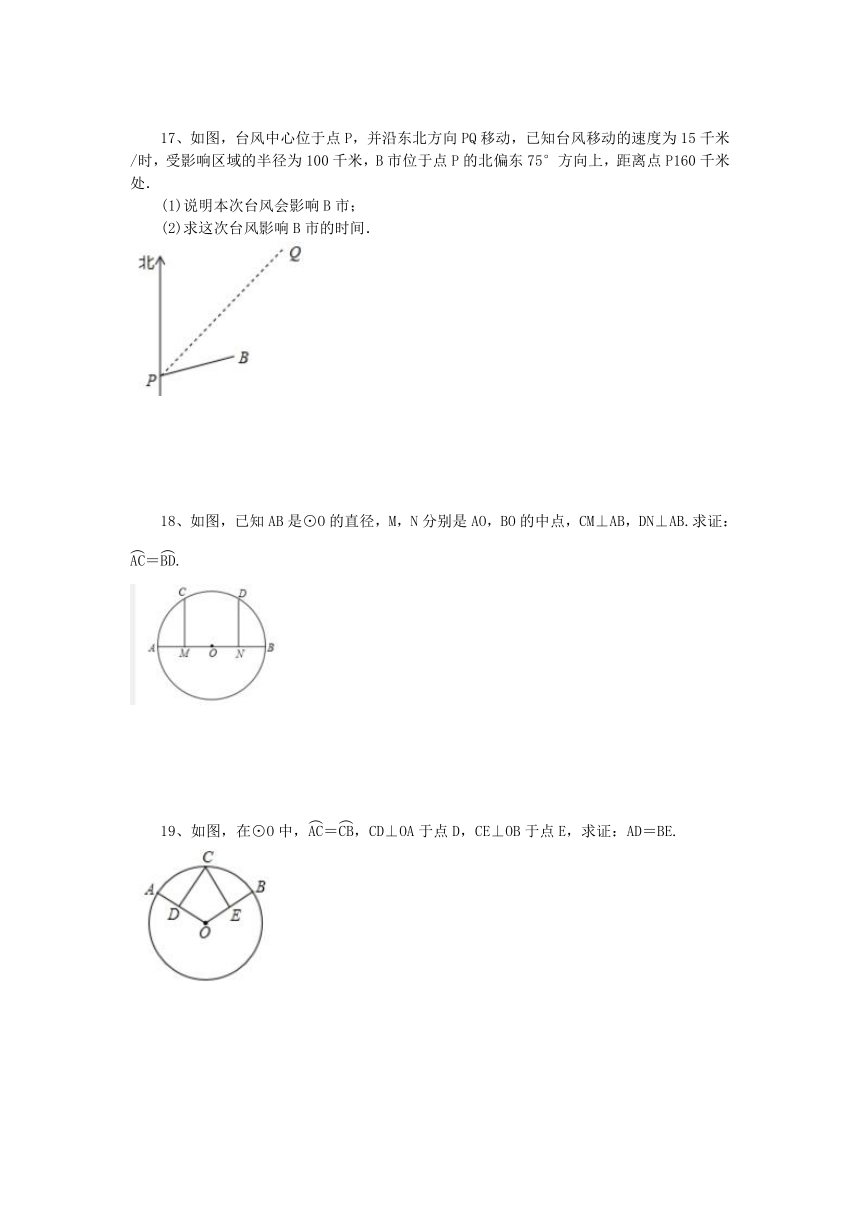
17、如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为15千米/时,受影响区域的半径为100千米,B市位于点P的北偏东75°方向上,距离点P160千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
18、如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证:=.
19、如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E,求证:AD=BE.
参考答案
北师大版九年级数学下册第三章
3.1圆
同步练习题
一、选择题
1、已知⊙O与点P在同一平面内,若⊙O的半径为5,线段OP的长为4,则点P(B)
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.在⊙O上或在⊙O内
2、下列说法错误的是(C)
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆叫做等圆
3、下列说法正确的是(B)
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的圆心角相等
4、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(D)
A.32°
B.60°
C.68°
D.64°
5、如图,在⊙O中,=2,则以下数量关系正确的是(C)
A.AB=AC
B.AC=2AB
C.AC<2AB
D.AC>2AB
6、如图,已知=,则AB与CD的关系为(A)
A.AB=CD
B.AB>CD
C.ABD.不能确定
7、如图,在矩形ABCD中,AB=8,BC=3,点P在边AB上,且BP=3AP.如果⊙P是以点P为圆心、PD为半径的圆,那么下列判断正确的是(C)
A.点B,C均在⊙P外
B.点B在⊙P外,点C在⊙P内
C.点B在⊙P内,点C在⊙P外
D.点B,C均在⊙P内
二、填空题
8、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是3<r<5;
9、已知点C在线段AB上,且0<AC<AB.如果⊙C经过点A,那么点B与⊙C的位置关系是点B在⊙C外.
10、如图,AB和DE是⊙O的直径,弦AC∥DE.若弦BE=3,则弦CE=3.
11、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是120°.
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.
13、如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C,D.若==,则∠P的大小为60°.
三、解答题
14、如图,Rt△ABC的两条直角边BC=3
cm,AC=4
cm,斜边AB上的高为CD.若以点C为圆心,分别以r1=2
cm,r2=2.4
cm,r3=3
cm为半径作圆,试判断点D与这三个圆的位置关系.
解:在Rt△ABC中,根据勾股定理,得AB=5
cm,则CD==2.4
cm.
①当r1=2
cm时,2.4>2,点D在圆外;
②当r2=2.4
cm时,点D在圆上;
③当r3=3
cm时,2.4<3,点D在圆内
15、如图,小虎牵着小狗上街,小虎的手臂与绳共2.5
m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
解:小狗在地面上环绕的圆的半径为
r==2.0(m),
S=πr2=4π(m2).
故小狗在平整的地面上活动的最大区域是以2.0
m为半径的圆,其面积为4π
m2.
如图:
16、如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,交AD,BC于点E,F,延长BA交⊙A于点G.求证:=.
证明:连接AF.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAF=∠AFB,∠GAE=∠ABF.
∴∠GAE=∠EAF.∴=.
17、如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为15千米/时,受影响区域的半径为100千米,B市位于点P的北偏东75°方向上,距离点P160千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
解:(1)作BH⊥PQ于点H,
在Rt△BHP中,
由条件知,PB=160千米,∠BPQ=75°-45°=30°,
∴BH=160sin30°=80千米<100千米.
∴本次台风会影响B市.
(2)若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束,
由(1)得BH=80千米,由条件得BP1=BP2=100千米,
∴P1P2=2=120(千米).
∴台风影响B市的时间t==8(小时).
答:台风影响B市的时间为8小时.
18、如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证:=.
证明:连接OC,OD,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,∴OM=ON.
∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL).
∴∠COM=∠DON.∴=.
19、如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E,求证:AD=BE.
证明:连接OC.
∵=,
∴∠AOC=∠BOC.
∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°.
在△COD和△COE中,
∴△COD≌△COE(AAS).∴OD=OE.
∵AO=BO,∴AD=BE.
3.1-3.2
同步练习题
一、选择题
1、已知⊙O与点P在同一平面内,若⊙O的半径为5,线段OP的长为4,则点P(
)
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.在⊙O上或在⊙O内
2、下列说法错误的是(
)
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆叫做等圆
3、下列说法正确的是(
)
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的圆心角相等
4、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(
)
A.32°
B.60°
C.68°
D.64°
5、如图,在⊙O中,=2,则以下数量关系正确的是(
)
A.AB=AC
B.AC=2AB
C.AC<2AB
D.AC>2AB
6、如图,已知=,则AB与CD的关系为(
)
A.AB=CD
B.AB>CD
C.AB
7、如图,在矩形ABCD中,AB=8,BC=3,点P在边AB上,且BP=3AP.如果⊙P是以点P为圆心、PD为半径的圆,那么下列判断正确的是(
)
A.点B,C均在⊙P外
B.点B在⊙P外,点C在⊙P内
C.点B在⊙P内,点C在⊙P外
D.点B,C均在⊙P内
二、填空题
8、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是____;
9、已知点C在线段AB上,且0<AC<AB.如果⊙C经过点A,那么点B与⊙C的位置关系是____.
10、如图,AB和DE是⊙O的直径,弦AC∥DE.若弦BE=3,则弦CE=____.
11、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是____
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是____
13、如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C,D.若==,则∠P的大小为____
三、解答题
14、如图,Rt△ABC的两条直角边BC=3
cm,AC=4
cm,斜边AB上的高为CD.若以点C为圆心,分别以r1=2
cm,r2=2.4
cm,r3=3
cm为半径作圆,试判断点D与这三个圆的位置关系.
15、如图,小虎牵着小狗上街,小虎的手臂与绳共2.5
m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
16、如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,交AD,BC于点E,F,延长BA交⊙A于点G.求证:=.
17、如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为15千米/时,受影响区域的半径为100千米,B市位于点P的北偏东75°方向上,距离点P160千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
18、如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证:=.
19、如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E,求证:AD=BE.
参考答案
北师大版九年级数学下册第三章
3.1圆
同步练习题
一、选择题
1、已知⊙O与点P在同一平面内,若⊙O的半径为5,线段OP的长为4,则点P(B)
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.在⊙O上或在⊙O内
2、下列说法错误的是(C)
A.圆有无数条直径
B.连接圆上任意两点之间的线段叫弦
C.过圆心的线段是直径
D.能够重合的圆叫做等圆
3、下列说法正确的是(B)
A.相等的圆心角所对的弧相等
B.在同圆中,等弧所对的圆心角相等
C.在同圆中,相等的弦所对的弧相等
D.相等的弦所对的圆心角相等
4、如图,AB,CD是⊙O的直径,=.若∠AOE=32°,则∠COE的度数是(D)
A.32°
B.60°
C.68°
D.64°
5、如图,在⊙O中,=2,则以下数量关系正确的是(C)
A.AB=AC
B.AC=2AB
C.AC<2AB
D.AC>2AB
6、如图,已知=,则AB与CD的关系为(A)
A.AB=CD
B.AB>CD
C.AB
7、如图,在矩形ABCD中,AB=8,BC=3,点P在边AB上,且BP=3AP.如果⊙P是以点P为圆心、PD为半径的圆,那么下列判断正确的是(C)
A.点B,C均在⊙P外
B.点B在⊙P外,点C在⊙P内
C.点B在⊙P内,点C在⊙P外
D.点B,C均在⊙P内
二、填空题
8、如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是3<r<5;
9、已知点C在线段AB上,且0<AC<AB.如果⊙C经过点A,那么点B与⊙C的位置关系是点B在⊙C外.
10、如图,AB和DE是⊙O的直径,弦AC∥DE.若弦BE=3,则弦CE=3.
11、如图,已知BD是⊙O的直径,点A,C在⊙O上,=,∠AOB=60°,则∠COD的度数是120°.
12、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.
13、如图,AB为⊙O的直径,△PAB的边PA,PB与⊙O的交点分别为C,D.若==,则∠P的大小为60°.
三、解答题
14、如图,Rt△ABC的两条直角边BC=3
cm,AC=4
cm,斜边AB上的高为CD.若以点C为圆心,分别以r1=2
cm,r2=2.4
cm,r3=3
cm为半径作圆,试判断点D与这三个圆的位置关系.
解:在Rt△ABC中,根据勾股定理,得AB=5
cm,则CD==2.4
cm.
①当r1=2
cm时,2.4>2,点D在圆外;
②当r2=2.4
cm时,点D在圆上;
③当r3=3
cm时,2.4<3,点D在圆内
15、如图,小虎牵着小狗上街,小虎的手臂与绳共2.5
m(手臂与拉直的绳子在一条直线上),手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
解:小狗在地面上环绕的圆的半径为
r==2.0(m),
S=πr2=4π(m2).
故小狗在平整的地面上活动的最大区域是以2.0
m为半径的圆,其面积为4π
m2.
如图:
16、如图,以?ABCD的顶点A为圆心,AB为半径作⊙A,交AD,BC于点E,F,延长BA交⊙A于点G.求证:=.
证明:连接AF.
∵AB=AF,
∴∠ABF=∠AFB.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAF=∠AFB,∠GAE=∠ABF.
∴∠GAE=∠EAF.∴=.
17、如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为15千米/时,受影响区域的半径为100千米,B市位于点P的北偏东75°方向上,距离点P160千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
解:(1)作BH⊥PQ于点H,
在Rt△BHP中,
由条件知,PB=160千米,∠BPQ=75°-45°=30°,
∴BH=160sin30°=80千米<100千米.
∴本次台风会影响B市.
(2)若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束,
由(1)得BH=80千米,由条件得BP1=BP2=100千米,
∴P1P2=2=120(千米).
∴台风影响B市的时间t==8(小时).
答:台风影响B市的时间为8小时.
18、如图,已知AB是⊙O的直径,M,N分别是AO,BO的中点,CM⊥AB,DN⊥AB.求证:=.
证明:连接OC,OD,
∵AB是⊙O的直径,M,N分别是AO,BO的中点,∴OM=ON.
∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°.
在Rt△OMC和Rt△OND中,
∴Rt△OMC≌Rt△OND(HL).
∴∠COM=∠DON.∴=.
19、如图,在⊙O中,=,CD⊥OA于点D,CE⊥OB于点E,求证:AD=BE.
证明:连接OC.
∵=,
∴∠AOC=∠BOC.
∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=90°.
在△COD和△COE中,
∴△COD≌△COE(AAS).∴OD=OE.
∵AO=BO,∴AD=BE.
