华东师大版七年级下册数学9.3.2用多种正多边形铺设地面教案
文档属性
| 名称 | 华东师大版七年级下册数学9.3.2用多种正多边形铺设地面教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 68.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览

文档简介
主备人:
课题:9.3.2用多种正多边形铺设地面
教学目标:
1、联系多边形的内角和与外角和公式,探索用多种正多边形拼地板的道理.
2、结合现实世界中的美丽图案,充分感受用正多边形拼地板的意义,体会用多种正多边形拼地板与一种正多边形拼地板的相互关系.
教学重、难点:
1、通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象等能力.
2、通过操作使学生发现能拼成一个平面图形的关键.
教学课时:1课时
教学方法: 讲授 合作探究
教学过程:
导入
小明家刚买了新房,准备装修,小明想把新房的地面铺上地板砖,所以他这段时间特别留心已铺了地板砖的地面.看了一些地板砖的铺设后,小明打算用多种正多边形的地砖来铺满新房的地面.请你帮小明想想,他可以买哪种形状的地板砖?为什么?
二、学习目标
正确运用多边形的内角和与外角和公式,掌握用多种正多边形拼地板的方法.
三、整体感知
自学教材90.91页内容,发现用多种正多边形拼地板的道理与方法。
四、合作探究
1.用正三角形和正六边形能铺满地面吗?为什么?
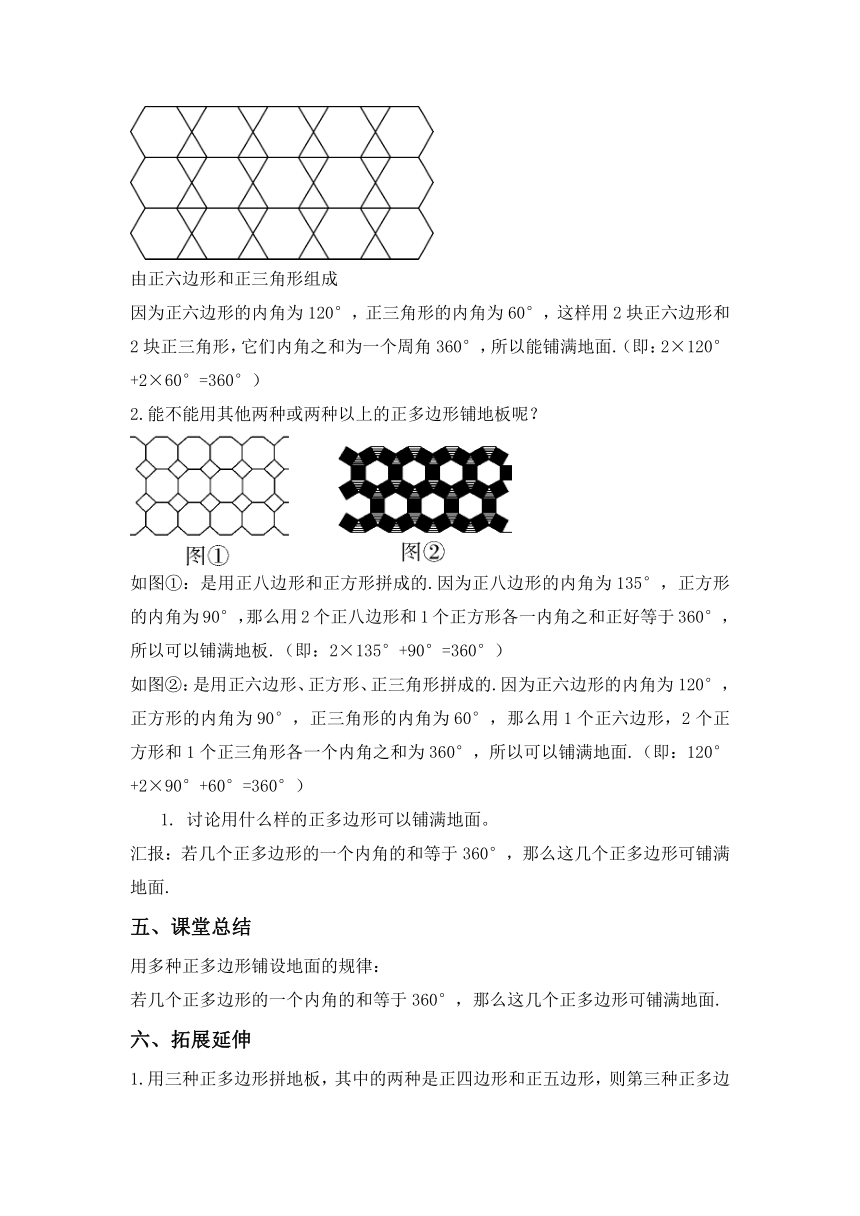
由正六边形和正三角形组成
因为正六边形的内角为120°,正三角形的内角为60°,这样用2块正六边形和2块正三角形,它们内角之和为一个周角360°,所以能铺满地面.(即:2×120°+2×60°=360°)
2.能不能用其他两种或两种以上的正多边形铺地板呢?
如图①:是用正八边形和正方形拼成的.因为正八边形的内角为135°,正方形的内角为90°,那么用2个正八边形和1个正方形各一内角之和正好等于360°,所以可以铺满地板.(即:2×135°+90°=360°)
如图②:是用正六边形、正方形、正三角形拼成的.因为正六边形的内角为120°,正方形的内角为90°,正三角形的内角为60°,那么用1个正六边形,2个正方形和1个正三角形各一个内角之和为360°,所以可以铺满地面.(即:120°+2×90°+60°=360°)
讨论用什么样的正多边形可以铺满地面。
汇报:若几个正多边形的一个内角的和等于360°,那么这几个正多边形可铺满地面.
五、课堂总结
用多种正多边形铺设地面的规律:
若几个正多边形的一个内角的和等于360°,那么这几个正多边形可铺满地面.
六、拓展延伸
1.用三种正多边形拼地板,其中的两种是正四边形和正五边形,则第三种正多边形的边数是( )
A.12 B.15
C.18 D.20
2.用m个正方形和n个正八边形铺满地面,则m、n满足的关系是( )
A.2m+3n=8 B.3m+2n=8
C.m+n=4 D.m+2n=6
七、当堂训练
1.我们知道用正三角形、正方形、正六边形合在一起可以铺满平面,若用正十边形、正八边形、正九边形合在一起,能不能铺满地面,为什么?
2.用正三角形、正方形、正六边形中至少一种铺满地面,有几种不同的选法?请写出来.
3.现有一批边长相等的正多边形瓷砖(如图所示),设计能铺满地面的瓷砖图案.
(1)能用相同的正多边形铺满地面的有 .
(2)从中任取两种来组合,能铺满地面的正多边形组合是 .
(3)从中任取三种来组合,能铺满地面的正多边形组合是 .
你能说出其中的数学道理吗?
八、作业布置
1.布置作业: 教材第91页“习题9.3”第1、2 题.
2.完成练习册中本课时练习.
九、板书设计
十、教学反思
课题:9.3.2用多种正多边形铺设地面
教学目标:
1、联系多边形的内角和与外角和公式,探索用多种正多边形拼地板的道理.
2、结合现实世界中的美丽图案,充分感受用正多边形拼地板的意义,体会用多种正多边形拼地板与一种正多边形拼地板的相互关系.
教学重、难点:
1、通过用两种以上正多边形拼地板,提高学生观察、分析、概括、抽象等能力.
2、通过操作使学生发现能拼成一个平面图形的关键.
教学课时:1课时
教学方法: 讲授 合作探究
教学过程:
导入
小明家刚买了新房,准备装修,小明想把新房的地面铺上地板砖,所以他这段时间特别留心已铺了地板砖的地面.看了一些地板砖的铺设后,小明打算用多种正多边形的地砖来铺满新房的地面.请你帮小明想想,他可以买哪种形状的地板砖?为什么?
二、学习目标
正确运用多边形的内角和与外角和公式,掌握用多种正多边形拼地板的方法.
三、整体感知
自学教材90.91页内容,发现用多种正多边形拼地板的道理与方法。
四、合作探究
1.用正三角形和正六边形能铺满地面吗?为什么?
由正六边形和正三角形组成
因为正六边形的内角为120°,正三角形的内角为60°,这样用2块正六边形和2块正三角形,它们内角之和为一个周角360°,所以能铺满地面.(即:2×120°+2×60°=360°)
2.能不能用其他两种或两种以上的正多边形铺地板呢?
如图①:是用正八边形和正方形拼成的.因为正八边形的内角为135°,正方形的内角为90°,那么用2个正八边形和1个正方形各一内角之和正好等于360°,所以可以铺满地板.(即:2×135°+90°=360°)
如图②:是用正六边形、正方形、正三角形拼成的.因为正六边形的内角为120°,正方形的内角为90°,正三角形的内角为60°,那么用1个正六边形,2个正方形和1个正三角形各一个内角之和为360°,所以可以铺满地面.(即:120°+2×90°+60°=360°)
讨论用什么样的正多边形可以铺满地面。
汇报:若几个正多边形的一个内角的和等于360°,那么这几个正多边形可铺满地面.
五、课堂总结
用多种正多边形铺设地面的规律:
若几个正多边形的一个内角的和等于360°,那么这几个正多边形可铺满地面.
六、拓展延伸
1.用三种正多边形拼地板,其中的两种是正四边形和正五边形,则第三种正多边形的边数是( )
A.12 B.15
C.18 D.20
2.用m个正方形和n个正八边形铺满地面,则m、n满足的关系是( )
A.2m+3n=8 B.3m+2n=8
C.m+n=4 D.m+2n=6
七、当堂训练
1.我们知道用正三角形、正方形、正六边形合在一起可以铺满平面,若用正十边形、正八边形、正九边形合在一起,能不能铺满地面,为什么?
2.用正三角形、正方形、正六边形中至少一种铺满地面,有几种不同的选法?请写出来.
3.现有一批边长相等的正多边形瓷砖(如图所示),设计能铺满地面的瓷砖图案.
(1)能用相同的正多边形铺满地面的有 .
(2)从中任取两种来组合,能铺满地面的正多边形组合是 .
(3)从中任取三种来组合,能铺满地面的正多边形组合是 .
你能说出其中的数学道理吗?
八、作业布置
1.布置作业: 教材第91页“习题9.3”第1、2 题.
2.完成练习册中本课时练习.
九、板书设计
十、教学反思
