华东师大版七年级下册数学教案 第10章 轴对称、平移与旋转 10.3.1图形的旋转
文档属性
| 名称 | 华东师大版七年级下册数学教案 第10章 轴对称、平移与旋转 10.3.1图形的旋转 |  | |
| 格式 | doc | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 12:27:50 | ||
图片预览


文档简介
主备人:
课题:10.3.1图形的旋转
教学目标:
知识与技能:
1.了解生活中旋转现象的存在,掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换;
2.会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋转角;
3.理解图形旋转的特征,并能利用旋转的特征解决问题。
过程与方法:
通过让学生欣赏和感受旋转实例,经历观察、猜想、交流、合作探究,从而归纳出旋转的特征,体会旋转变换对研究图形变化的重要性。
情感态度与价值观:
经历对生活中旋转图形的观察、讨论,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感;通过小组合作交流活动,培养学生合作学习的意识和合作探索的习惯。
教学重、难点:
重点:掌握旋转的有关概念,会准确找出对应点、对应线段、对应角,旋转中心、旋转角.
难点:理解“图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度”,会准确找出旋转角.
教学课时: 1课时
教学方法:先学后教 当堂训练
教学过程:
观图激趣,设疑导入
1、用课件显示日常生活中部分物体的旋转现象。(见课件)
观看后,请思考:(1)在这些运动中有哪些共同特征?(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
2、下面两幅图案漂亮吗?你有兴趣知道它们是如何生成的吗?
利用多媒体动画演示上面两幅图案的生成过程,引入课题:图形的旋转
[设计意图]:激发学生的学习兴趣,为新知识的学习作好铺垫。
二、出示学习目标
1.了解生活中旋转现象的存在,掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换;
2.会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋转角;
3.理解图形旋转的特征,并能利用旋转的特征解决问题。
三、整体感知来
观察:单摆上小球的运动。(动画演示)
问题:
(1)单摆上小球的转动由位置A转到A′,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度?
(2)观察了荡秋千、风扇、风车与单摆的运动后,你知道什么是旋转、旋转中心以及旋转角吗?
(引导学生小组讨论并概括出旋转、旋转中心和旋转角的概念。)※归纳得出:
知识点1:旋转的概念
在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形运动叫做图形的旋转。这个定点称为旋转中心,所转动的角度称为旋转角度。
知识点2:旋转的三要素:旋转中心、旋转方向、旋转角度。
知识点3:旋转中的对应关系
如图,△CDO绕点O逆时针旋转45°得到△ABO,在这样的旋转过程中,你发现了什么?
可以看到点C旋转到A,OD旋转到OB,∠COD旋转到∠AOB,这些都是互相对应的点、线段与角。此时,
点D的对应点是
线段OD的对应线段是
线段CD的对应线段是
∠COD的对应角是
∠C的对应角是
旋转中心是点
旋转的角度是
[设计意图]:通过观察单摆上小球的运动过程使学生形象、直观地理解旋转的有关概念。k.Com]
四、合作探究[
1、举例应用,加深认识
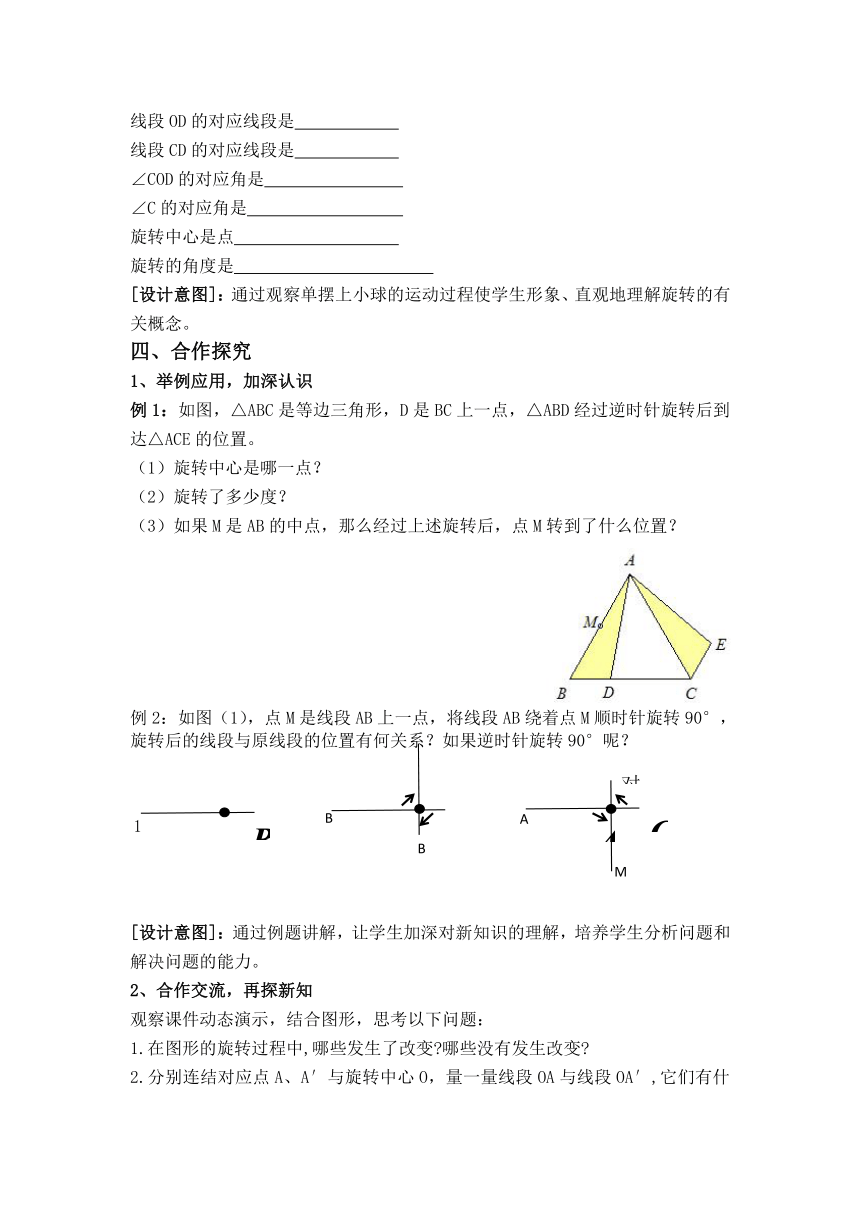
例1:如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
例2:如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
[设计意图]:通过例题讲解,让学生加深对新知识的理解,培养学生分析问题和解决问题的能力。
2、合作交流,再探新知
观察课件动态演示,结合图形,思考以下问题:
1.在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
2.分别连结对应点A、A′与旋转中心O,量一量线段OA与线段OA′,它们有什么关系?任意找一对对应点,量一下它们与旋转中心的连线段,你能发现什么规律?
3.量一下∠AOA′的度数,再任意找几对对应点,分别量一下对应点与旋转中心连线段的度数,你又能发现什么规律?
※归纳得出:
知识点4:旋转的特征
(1)旋转前后图形的形状和大小不变。
即对应线段相等,对应角相等。
(2)对应点到旋转中心的距离相等。
(3)图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度。
即对应点与旋转中心连线段的夹角等于旋转角.
[设计意图]:课件演示及学生的动手操作,培养学生观察能力和探究问题的能力、动手能力,以及与人合作交流的能力。充分体现了教师为主导,学生为主体的教学思想,同时也突出重点,突破难点。
五、课堂总结
(教师引导学生总结、归纳、反思。)
[设计意图]:充分发挥学生的主体作用,加深对本课内容的理解,提高学生的概括能力、表达能力。
拓展延伸
1、钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
2、△ABC是等边三角形, △ABP顺时针旋转后能与△CBP’重合,那么
(1)旋转中心是哪一点?
(2)旋转角是多少?
(3)连接PP’后,△BPP’是什么三角形?
3. 必做题:如图,在正方形ABCD中,E是CB延长线上一点,△ABE沿顺时针方向旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别移动到什么位置?
(5)若点G是线段BE的中点,经过旋转后,点G移到了什么位置?请在图形上作出.
(6)连结EF,请判断△AEF的形状,并说明理由.
(7)试判断四边形ABCD与AFCE面积的大小关系.
4、选做题:如图是一个直角三角形的苗圃,由正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少??
[设计意图]:
①巩固所学知识,发现和弥补教与学中的遗漏和不足;
②针对学生素质的差异进行分层训练,既使学生掌握基础知识,又使学有余力的学生有所提高,从而贯彻因材施教的原则。
七、当堂训练
1、如图,△ABC按逆时针方向转动一个角后成为△AB′C′,图中哪一点是旋转中心?请指出一个旋转角。
2、如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
[设计意图]:通过练习让学生再次明确旋转的主要因素,从而让学生在知识不断重现的基础上加深理解,形成能力,实现本课的知识目标。
八、作业布置:
1、完成练习册本课时的习题.
九、板书设计:
10.3 图形的旋转
1、旋转的概念:
2、旋转的三要素:旋转中心、旋转方向、旋转角。
十、教学反思:
课题:10.3.1图形的旋转
教学目标:
知识与技能:
1.了解生活中旋转现象的存在,掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换;
2.会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋转角;
3.理解图形旋转的特征,并能利用旋转的特征解决问题。
过程与方法:
通过让学生欣赏和感受旋转实例,经历观察、猜想、交流、合作探究,从而归纳出旋转的特征,体会旋转变换对研究图形变化的重要性。
情感态度与价值观:
经历对生活中旋转图形的观察、讨论,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感;通过小组合作交流活动,培养学生合作学习的意识和合作探索的习惯。
教学重、难点:
重点:掌握旋转的有关概念,会准确找出对应点、对应线段、对应角,旋转中心、旋转角.
难点:理解“图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度”,会准确找出旋转角.
教学课时: 1课时
教学方法:先学后教 当堂训练
教学过程:
观图激趣,设疑导入
1、用课件显示日常生活中部分物体的旋转现象。(见课件)
观看后,请思考:(1)在这些运动中有哪些共同特征?(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
2、下面两幅图案漂亮吗?你有兴趣知道它们是如何生成的吗?
利用多媒体动画演示上面两幅图案的生成过程,引入课题:图形的旋转
[设计意图]:激发学生的学习兴趣,为新知识的学习作好铺垫。
二、出示学习目标
1.了解生活中旋转现象的存在,掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换;
2.会找出旋转前后图形中的对应点、对应线段、对应角、旋转中心、旋转角;
3.理解图形旋转的特征,并能利用旋转的特征解决问题。
三、整体感知来
观察:单摆上小球的运动。(动画演示)
问题:
(1)单摆上小球的转动由位置A转到A′,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度?
(2)观察了荡秋千、风扇、风车与单摆的运动后,你知道什么是旋转、旋转中心以及旋转角吗?
(引导学生小组讨论并概括出旋转、旋转中心和旋转角的概念。)※归纳得出:
知识点1:旋转的概念
在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形运动叫做图形的旋转。这个定点称为旋转中心,所转动的角度称为旋转角度。
知识点2:旋转的三要素:旋转中心、旋转方向、旋转角度。
知识点3:旋转中的对应关系
如图,△CDO绕点O逆时针旋转45°得到△ABO,在这样的旋转过程中,你发现了什么?
可以看到点C旋转到A,OD旋转到OB,∠COD旋转到∠AOB,这些都是互相对应的点、线段与角。此时,
点D的对应点是
线段OD的对应线段是
线段CD的对应线段是
∠COD的对应角是
∠C的对应角是
旋转中心是点
旋转的角度是
[设计意图]:通过观察单摆上小球的运动过程使学生形象、直观地理解旋转的有关概念。k.Com]
四、合作探究[
1、举例应用,加深认识
例1:如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
例2:如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转90°呢?
[设计意图]:通过例题讲解,让学生加深对新知识的理解,培养学生分析问题和解决问题的能力。
2、合作交流,再探新知
观察课件动态演示,结合图形,思考以下问题:
1.在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
2.分别连结对应点A、A′与旋转中心O,量一量线段OA与线段OA′,它们有什么关系?任意找一对对应点,量一下它们与旋转中心的连线段,你能发现什么规律?
3.量一下∠AOA′的度数,再任意找几对对应点,分别量一下对应点与旋转中心连线段的度数,你又能发现什么规律?
※归纳得出:
知识点4:旋转的特征
(1)旋转前后图形的形状和大小不变。
即对应线段相等,对应角相等。
(2)对应点到旋转中心的距离相等。
(3)图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度。
即对应点与旋转中心连线段的夹角等于旋转角.
[设计意图]:课件演示及学生的动手操作,培养学生观察能力和探究问题的能力、动手能力,以及与人合作交流的能力。充分体现了教师为主导,学生为主体的教学思想,同时也突出重点,突破难点。
五、课堂总结
(教师引导学生总结、归纳、反思。)
[设计意图]:充分发挥学生的主体作用,加深对本课内容的理解,提高学生的概括能力、表达能力。
拓展延伸
1、钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
2、△ABC是等边三角形, △ABP顺时针旋转后能与△CBP’重合,那么
(1)旋转中心是哪一点?
(2)旋转角是多少?
(3)连接PP’后,△BPP’是什么三角形?
3. 必做题:如图,在正方形ABCD中,E是CB延长线上一点,△ABE沿顺时针方向旋转后得到△ADF,请按图回答:
(1)旋转中心是哪一点?
(2)旋转角是多少度?
(3)∠EAF等于多少度?
(4)经过旋转,点B与点E分别移动到什么位置?
(5)若点G是线段BE的中点,经过旋转后,点G移到了什么位置?请在图形上作出.
(6)连结EF,请判断△AEF的形状,并说明理由.
(7)试判断四边形ABCD与AFCE面积的大小关系.
4、选做题:如图是一个直角三角形的苗圃,由正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少??
[设计意图]:
①巩固所学知识,发现和弥补教与学中的遗漏和不足;
②针对学生素质的差异进行分层训练,既使学生掌握基础知识,又使学有余力的学生有所提高,从而贯彻因材施教的原则。
七、当堂训练
1、如图,△ABC按逆时针方向转动一个角后成为△AB′C′,图中哪一点是旋转中心?请指出一个旋转角。
2、如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
[设计意图]:通过练习让学生再次明确旋转的主要因素,从而让学生在知识不断重现的基础上加深理解,形成能力,实现本课的知识目标。
八、作业布置:
1、完成练习册本课时的习题.
九、板书设计:
10.3 图形的旋转
1、旋转的概念:
2、旋转的三要素:旋转中心、旋转方向、旋转角。
十、教学反思:
