第五章生活中的轴对称小结与复习同课异构的教研课件(共14张PPT)
文档属性
| 名称 | 第五章生活中的轴对称小结与复习同课异构的教研课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 122.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 22:41:02 | ||
图片预览




文档简介
(共14张PPT)
小结与复习
第五章
生活中的轴对称
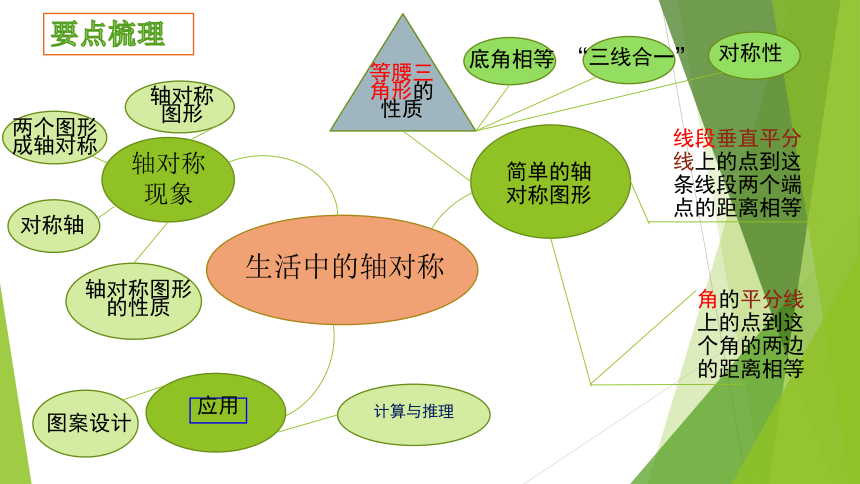
要点梳理
生活中的轴对称
轴对称现象
对称轴
轴对称图形
两个图形成轴对称
轴对称图形的性质
应用
计算与推理
图案设计
等腰三角形的性质
线段垂直平分线上的点到这条线段两个端点的距离相等
角的平分线上的点到这个角的两边的距离相等
底角相等
“三线合一”
简单的轴
对称图形
对称性
考点一
轴对称图形与轴对称
例1
如图(1),方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)写出AA1的长度,求出△ABC的面积;
(3)如图(2),A、C是直线MN同侧固定的点,B是直线MN上的一个动点,在直线MN上画出点B,使AB+BC最小.
.
考点讲练
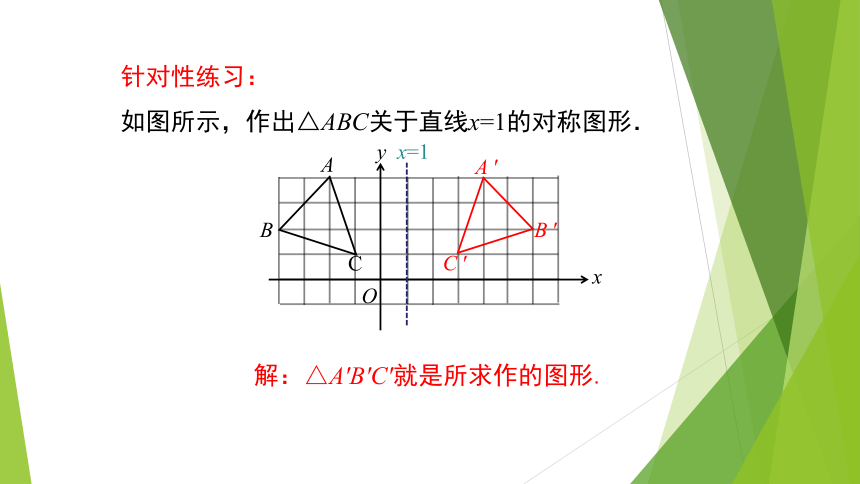
针对性练习:
如图所示,作出△ABC关于直线x=1的对称图形.
x
y
O
x=1
A
B
C
A
′
B
′
C
′
解:△A′B′C′就是所求作的图形.
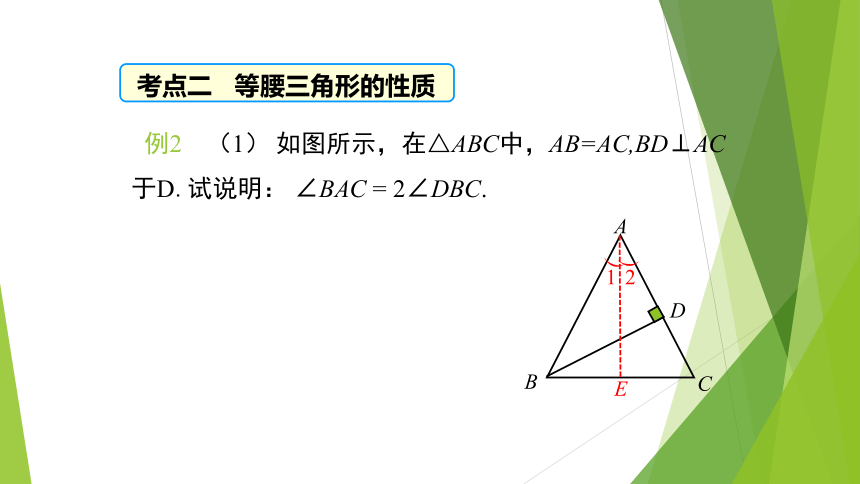
考点二
等腰三角形的性质
例2
(1)
如图所示,在△ABC中,AB=AC,BD⊥AC于D.试说明:
∠BAC
=
2∠DBC.
A
B
C
D
)
)
1
2
E
(2)若等腰三角形的两边长分别为4和6,求它的周长.
针对性练习:
等腰三角形的周长为20cm,其中两边的差为8cm,求这个等腰三角形各边的长.
例3
(1)
有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置(保留作图痕迹,不要求写出画法).
考点三
线段垂直平分线与角平分线的性质
例4
已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.
求证:∠BAF=∠ACF.
3.如图,在△ABC中,DE是AC的垂直平分线,AC=5厘米,△ABD的周长等于13厘米,则△ABC的周长是
.
C
18厘米
A
B
D
E
针对训练
4.
如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
考点四
本章的数学思想与解题方法
分类讨论思想
例5如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
1.等腰三角形中,有一个角是40°,它的一条腰上的高与底边的夹角是( )
A.20°B.50°
C.25°或40°
D.20°或50°
2.已知△ABC是等腰三角形,它的周长为20cm,一条边长6cm,那么腰长是多少?
针对训练
课后小卷复习作业
课后作业
小结与复习
第五章
生活中的轴对称
要点梳理
生活中的轴对称
轴对称现象
对称轴
轴对称图形
两个图形成轴对称
轴对称图形的性质
应用
计算与推理
图案设计
等腰三角形的性质
线段垂直平分线上的点到这条线段两个端点的距离相等
角的平分线上的点到这个角的两边的距离相等
底角相等
“三线合一”
简单的轴
对称图形
对称性
考点一
轴对称图形与轴对称
例1
如图(1),方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)写出AA1的长度,求出△ABC的面积;
(3)如图(2),A、C是直线MN同侧固定的点,B是直线MN上的一个动点,在直线MN上画出点B,使AB+BC最小.
.
考点讲练
针对性练习:
如图所示,作出△ABC关于直线x=1的对称图形.
x
y
O
x=1
A
B
C
A
′
B
′
C
′
解:△A′B′C′就是所求作的图形.
考点二
等腰三角形的性质
例2
(1)
如图所示,在△ABC中,AB=AC,BD⊥AC于D.试说明:
∠BAC
=
2∠DBC.
A
B
C
D
)
)
1
2
E
(2)若等腰三角形的两边长分别为4和6,求它的周长.
针对性练习:
等腰三角形的周长为20cm,其中两边的差为8cm,求这个等腰三角形各边的长.
例3
(1)
有公路l1同侧、l2异侧的两个城镇A,B,如图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置(保留作图痕迹,不要求写出画法).
考点三
线段垂直平分线与角平分线的性质
例4
已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.
求证:∠BAF=∠ACF.
3.如图,在△ABC中,DE是AC的垂直平分线,AC=5厘米,△ABD的周长等于13厘米,则△ABC的周长是
.
C
18厘米
A
B
D
E
针对训练
4.
如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
考点四
本章的数学思想与解题方法
分类讨论思想
例5如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
1.等腰三角形中,有一个角是40°,它的一条腰上的高与底边的夹角是( )
A.20°B.50°
C.25°或40°
D.20°或50°
2.已知△ABC是等腰三角形,它的周长为20cm,一条边长6cm,那么腰长是多少?
针对训练
课后小卷复习作业
课后作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
