五年级数学下册课件 - 质数和合数 人教版(共18张PPT)
文档属性
| 名称 | 五年级数学下册课件 - 质数和合数 人教版(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 20:59:25 | ||
图片预览






文档简介
(共18张PPT)
质数和合数
找出20和81的因数。
一、复习导入,揭示课题
20的因数有哪些?81的呢?
20÷1=20
20÷2=10
20÷4=5
20的因数有:1,2,4,5,10,20。
1×81=81
3×27=81
9×9=91
81的因数有:1,3,9,27,81。
你还记得什么是因数?什么是倍数吗?
在整数除法中,如果商是整数而没有余数,就说除数和商是被除数的因数,被除数是除数和商的倍数。
1、自然数1~20中,奇数有哪些?偶数有哪些?
奇数
偶数
2、想一想:自然数分成偶数和奇数,是按什么标准分的?
自然数分成偶数和奇数是按2的倍数来分的。
1
3
5
7
9
11
13
15
17
19
2
4
6
8
10
12
14
16
18
20
一、复习导入,揭示课题
二、探究新知
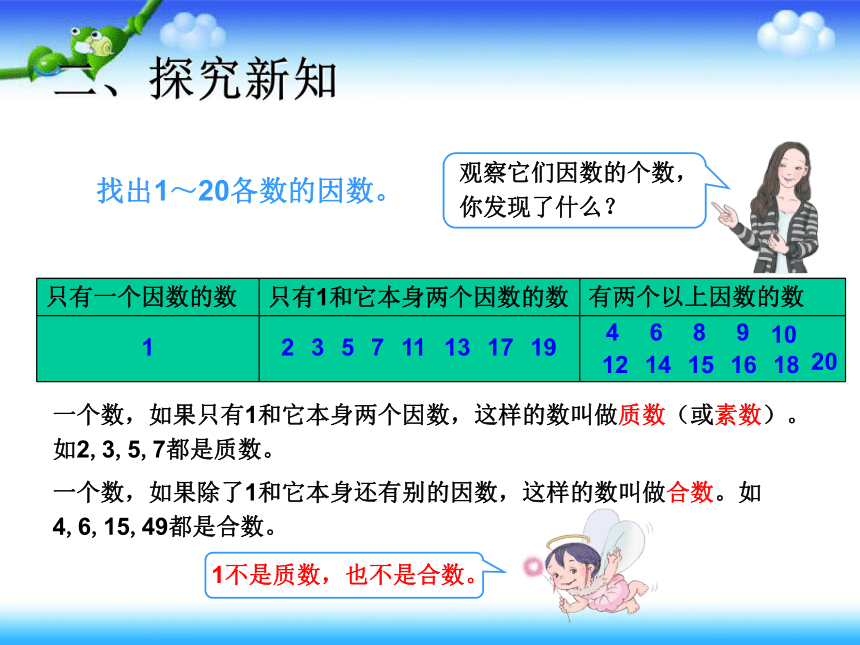
找出1~20各数的因数。
1的因数有:1
2的因数有:1,2
3的因数有:1,3
4的因数有:1,2,4
5的因数有:1,5
6的因数有:1,2,3,6
7的因数有:1,7
8的因数有:1,2,4,8
9的因数有:1,3,9
10的因数有:1,2,5,10
11的因数有:1,11
12的因数有:1,2,3,4,6,12
13的因数有:1,13
14的因数有:1,2,7,14
15的因数有:1,3,5,15
16的因数有:1,2,4,8,16
17的因数有:1,17
18的因数有:1,2,3,6,9,18
19的因数有:1,19
20的因数有:1,2,4,5,10,20
观察它们因数的个数,你发现了什么?
根据因数的个数把这20个数进行分类,可以怎样分?小组讨论。
二、探究新知
只有一个因数的数
只有1和它本身两个因数的数
有两个以上因数的数
1
2
3
5
7
11
13
17
19
4
6
8
9
10
12
14
15
16
18
找出1~20各数的因数。
观察它们因数的个数,你发现了什么?
根据因数的个数把这20个数进行分类,可以怎样分?小组讨论。
20
二、探究新知
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。如2,3,5,7都是质数。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,15,49都是合数。
只有一个因数的数
只有1和它本身两个因数的数
有两个以上因数的数
1
2
3
5
7
11
13
17
19
4
6
8
9
10
12
14
15
16
18
找出1~20各数的因数。
观察它们因数的个数,你发现了什么?
1不是质数,也不是合数。
20
判断下列各数中哪些是质数,哪些是合数。
17
22
29
35
37
87
93
96
质数:
17,29,37
合数:
22,35,87,93,96
二、探究新知
找出100以内的质数,做一个质数表。
可以把每个数都验证一下,看哪些是质数。
先把2的倍数画去,但2除外,画掉的这些数都不是质数。3的倍数也可以……
画到几的倍数就可以了?
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
100以内质数表
质数
合数
1
奇数
偶数
自然数
(按因数的个数分类)
自然数
(按2的倍数分类)
1.下面的说法正确吗?说说你的理由。
(1)所有的奇数都是质数。
(2)所有的偶数都是合数。
(3)在1,2,3,4,5,…中,除了质数以
外都是合数。
(4)两个质数的和是偶数。
2.
将下面各数分别填入指定的圈里。
27
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
质数
合数
奇数
偶数
27
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
37
41
27
61
73
83
95
11
33
47
57
87
99
58
14
62
我们两个的
和是
10。
3.
你知道它们各是多少吗?
我们两个的积是
21。
我们两个的
和是
20。
我们两个的积是
91。
3
和
7
13
和
7
我是最小
的质数。
2
4
我是最小的合数。
猜一猜老师的手机号码是多少?
(1)第一、三、八、九位,既不是质数也不是合数;
(2)第二、四位,比最小的质数大1;
(3)第五位,比最小的合数大1;
(4)第六位是10以内最大的质数;
(5)第七位是10以内最大的奇数;
(6)第十位是偶数,但不是合数;
(7)第十一位,最小的自然数。
1
1
1
1
3
3
5
7
9
2
0
5.
偶数
10。
3
+
7
=
10
两人一组,一人给出大于
2
的偶数,另一人找出和为此数的两个质数。
从上面的游戏我们看到:4
=
2
+
2,6
=
3
+
3,8
=
5
+
3,10
=
7
+
3,12
=
7
+
5,14
=
11
+
3
······
那么,是不是所有大于
2
的偶数,都可以表示为两个质数的和呢?
哥德巴赫猜想
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。哥德巴赫猜想看似简单,要证明却非常困难,成为数学中一个著名的难题,被称为
“数学王冠上
的明珠”。
世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
谢谢大家
2016.03.01
质数和合数
找出20和81的因数。
一、复习导入,揭示课题
20的因数有哪些?81的呢?
20÷1=20
20÷2=10
20÷4=5
20的因数有:1,2,4,5,10,20。
1×81=81
3×27=81
9×9=91
81的因数有:1,3,9,27,81。
你还记得什么是因数?什么是倍数吗?
在整数除法中,如果商是整数而没有余数,就说除数和商是被除数的因数,被除数是除数和商的倍数。
1、自然数1~20中,奇数有哪些?偶数有哪些?
奇数
偶数
2、想一想:自然数分成偶数和奇数,是按什么标准分的?
自然数分成偶数和奇数是按2的倍数来分的。
1
3
5
7
9
11
13
15
17
19
2
4
6
8
10
12
14
16
18
20
一、复习导入,揭示课题
二、探究新知
找出1~20各数的因数。
1的因数有:1
2的因数有:1,2
3的因数有:1,3
4的因数有:1,2,4
5的因数有:1,5
6的因数有:1,2,3,6
7的因数有:1,7
8的因数有:1,2,4,8
9的因数有:1,3,9
10的因数有:1,2,5,10
11的因数有:1,11
12的因数有:1,2,3,4,6,12
13的因数有:1,13
14的因数有:1,2,7,14
15的因数有:1,3,5,15
16的因数有:1,2,4,8,16
17的因数有:1,17
18的因数有:1,2,3,6,9,18
19的因数有:1,19
20的因数有:1,2,4,5,10,20
观察它们因数的个数,你发现了什么?
根据因数的个数把这20个数进行分类,可以怎样分?小组讨论。
二、探究新知
只有一个因数的数
只有1和它本身两个因数的数
有两个以上因数的数
1
2
3
5
7
11
13
17
19
4
6
8
9
10
12
14
15
16
18
找出1~20各数的因数。
观察它们因数的个数,你发现了什么?
根据因数的个数把这20个数进行分类,可以怎样分?小组讨论。
20
二、探究新知
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。如2,3,5,7都是质数。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,15,49都是合数。
只有一个因数的数
只有1和它本身两个因数的数
有两个以上因数的数
1
2
3
5
7
11
13
17
19
4
6
8
9
10
12
14
15
16
18
找出1~20各数的因数。
观察它们因数的个数,你发现了什么?
1不是质数,也不是合数。
20
判断下列各数中哪些是质数,哪些是合数。
17
22
29
35
37
87
93
96
质数:
17,29,37
合数:
22,35,87,93,96
二、探究新知
找出100以内的质数,做一个质数表。
可以把每个数都验证一下,看哪些是质数。
先把2的倍数画去,但2除外,画掉的这些数都不是质数。3的倍数也可以……
画到几的倍数就可以了?
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47
53
59
61
67
71
73
79
83
89
97
100以内质数表
质数
合数
1
奇数
偶数
自然数
(按因数的个数分类)
自然数
(按2的倍数分类)
1.下面的说法正确吗?说说你的理由。
(1)所有的奇数都是质数。
(2)所有的偶数都是合数。
(3)在1,2,3,4,5,…中,除了质数以
外都是合数。
(4)两个质数的和是偶数。
2.
将下面各数分别填入指定的圈里。
27
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
质数
合数
奇数
偶数
27
37
41
58
61
73
83
95
11
14
33
47
57
62
87
99
37
41
27
61
73
83
95
11
33
47
57
87
99
58
14
62
我们两个的
和是
10。
3.
你知道它们各是多少吗?
我们两个的积是
21。
我们两个的
和是
20。
我们两个的积是
91。
3
和
7
13
和
7
我是最小
的质数。
2
4
我是最小的合数。
猜一猜老师的手机号码是多少?
(1)第一、三、八、九位,既不是质数也不是合数;
(2)第二、四位,比最小的质数大1;
(3)第五位,比最小的合数大1;
(4)第六位是10以内最大的质数;
(5)第七位是10以内最大的奇数;
(6)第十位是偶数,但不是合数;
(7)第十一位,最小的自然数。
1
1
1
1
3
3
5
7
9
2
0
5.
偶数
10。
3
+
7
=
10
两人一组,一人给出大于
2
的偶数,另一人找出和为此数的两个质数。
从上面的游戏我们看到:4
=
2
+
2,6
=
3
+
3,8
=
5
+
3,10
=
7
+
3,12
=
7
+
5,14
=
11
+
3
······
那么,是不是所有大于
2
的偶数,都可以表示为两个质数的和呢?
哥德巴赫猜想
这个问题是德国数学家哥德巴赫最先提出的,所以被称作哥德巴赫猜想。哥德巴赫猜想看似简单,要证明却非常困难,成为数学中一个著名的难题,被称为
“数学王冠上
的明珠”。
世界各国的数学家都想攻克这一难题,但至今还未解决。我国数学家陈景润在这一领域取得了举世瞩目的成果。
谢谢大家
2016.03.01
