19.2.2 一次函数3-2020-2021学年人教版八年级数学下册导学案(word版含答案)
文档属性
| 名称 | 19.2.2 一次函数3-2020-2021学年人教版八年级数学下册导学案(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 74.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 10:34:44 | ||
图片预览


文档简介
授课人 年级 八 学科 数学 授课时间
课题 19.2.2 一次函数3 课型 新授
学习 目标 会用待定系数法求一次函数解析式。
利用一次函数知识解决相关实际问题.
学习 关键 重点 待定系数法求一次函数解析式,用一次函数知识解决相关问题。
难点 用一次函数知识解决相关问题。
学教过程
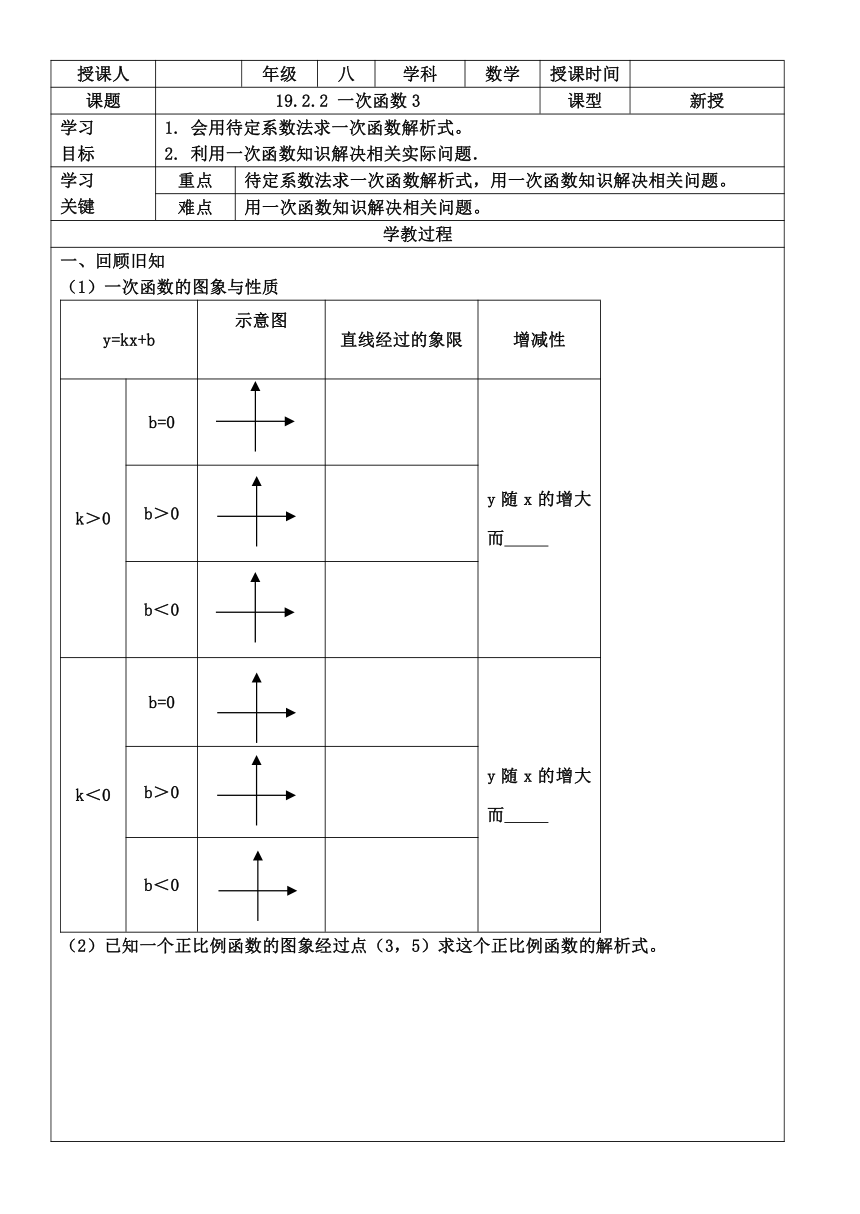
回顾旧知 (1)一次函数的图象与性质
y=kx+b
示意图
直线经过的象限
增减性
k>0
b=0
y随x的增大而
b>0
b<0
k<0
b=0
y随x的增大而
b>0
b<0
已知一个正比例函数的图象经过点(3,5)求这个正比例函数的解析式。
自学新知
阅读课本P93 ~94 页,总结归纳待定系数法求一次函数解析式的步骤:
1:设——设一次函数解析式为y=kx+b(k≠0);
2:代——代入两个点的坐标,列出关于k , b 的二元一次方程组;
3:解——解这个二元一次方程组,求出k, b;
4:写——据求出的 k, b的值,写出所求的解析式.
巩固练习
1.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5),求当x=5时,函数y的值.
2 已知一次函数的图象如下图,写出它的关系式.
3.已知一次函数的图象经过点(9,0)和(24,20),写出函数解析式。
四、当堂达标
1.(8分)已知y-100与x成正比例,且当x=10时,y=600.
(1)求y关于x的函数解析式.
(2)当-300<y≤400时, 自变量x的取值范围。
2.(8分)为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .
答案:
解:设正比例函数解析式为 y=kx,由已知得:5=3k,
解得:k=, ∴正比例函数解析式为 y=x
1.解 由题意,得
解这个方程组,得
这个函数解析式为y=-3x-2.
当x=5时,y=-3×5-2=-17.
2.解 设:所求的一次函数的解析式为y=kx+b(k≠0).
直线经过点(2,0),(0,-3),把这两点坐标代入解析式,得
解得
所以所求的一次函数的关系式是.
3.
1.(1)设这个正比例函数解析式为 y-100=kx
把x=10时,y=600代入y-100=kx,得
600-100=10k
解得k=50
∴y-100=50x
即y=50x+100
(2)当-300<y≤400时, -300<50x+100 ≤400
∴自变量x的取值范围为-8<x≤6
2.0.5元/度、0.9元/度
课题 19.2.2 一次函数3 课型 新授
学习 目标 会用待定系数法求一次函数解析式。
利用一次函数知识解决相关实际问题.
学习 关键 重点 待定系数法求一次函数解析式,用一次函数知识解决相关问题。
难点 用一次函数知识解决相关问题。
学教过程
回顾旧知 (1)一次函数的图象与性质
y=kx+b
示意图
直线经过的象限
增减性
k>0
b=0
y随x的增大而
b>0
b<0
k<0
b=0
y随x的增大而
b>0
b<0
已知一个正比例函数的图象经过点(3,5)求这个正比例函数的解析式。
自学新知
阅读课本P93 ~94 页,总结归纳待定系数法求一次函数解析式的步骤:
1:设——设一次函数解析式为y=kx+b(k≠0);
2:代——代入两个点的坐标,列出关于k , b 的二元一次方程组;
3:解——解这个二元一次方程组,求出k, b;
4:写——据求出的 k, b的值,写出所求的解析式.
巩固练习
1.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5),求当x=5时,函数y的值.
2 已知一次函数的图象如下图,写出它的关系式.
3.已知一次函数的图象经过点(9,0)和(24,20),写出函数解析式。
四、当堂达标
1.(8分)已知y-100与x成正比例,且当x=10时,y=600.
(1)求y关于x的函数解析式.
(2)当-300<y≤400时, 自变量x的取值范围。
2.(8分)为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .
答案:
解:设正比例函数解析式为 y=kx,由已知得:5=3k,
解得:k=, ∴正比例函数解析式为 y=x
1.解 由题意,得
解这个方程组,得
这个函数解析式为y=-3x-2.
当x=5时,y=-3×5-2=-17.
2.解 设:所求的一次函数的解析式为y=kx+b(k≠0).
直线经过点(2,0),(0,-3),把这两点坐标代入解析式,得
解得
所以所求的一次函数的关系式是.
3.
1.(1)设这个正比例函数解析式为 y-100=kx
把x=10时,y=600代入y-100=kx,得
600-100=10k
解得k=50
∴y-100=50x
即y=50x+100
(2)当-300<y≤400时, -300<50x+100 ≤400
∴自变量x的取值范围为-8<x≤6
2.0.5元/度、0.9元/度
