19.2.3.1一次函数与一元一次方程-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 19.2.3.1一次函数与一元一次方程-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 10:27:47 | ||
图片预览

文档简介
授课人 年级 八 学科 数学 授课时间
课题 19.2.3一次函数与一元一次方程 课型 新授
学习 目标 1、理解一次函数与一元一次方程的关系。
2、会根据一次函数的图像解决一元一次方程的求解。
学习 关键 重点 1、理解一次函数与一元一次方程的关系。
2、会根据一次函数的图像解决一元一次方程的求解。
难点 一次函数与一元一次方程的关系的发现、归纳、和运用
学教过程
探究新知 1.问题1:解方程2x+20=0 它的解为 。
问题2:自变量x为何值时,函数y=2x+20的值为0?
联想:问题(1),(2)是同一个问题吗?
问题3:画出直线y=2x+20的图像,并确定它与x轴交点的坐标。
2、知识点的归纳总结:
由于任何一元一次方程都可以转化为 的形式,所以解一元一次方程可以转化为求一次函数 函数值为0时的相应的自变量的值。
从图像上看,这又相当于求直线y= 与 轴交点的横坐标。
简言之:求一元一次方程的解就是求一次函数与x轴交点的横坐标。
二、巩固练习
1.已知方程ax+b=0的解是-2,下列图象肯定不是直线 y=ax+b的是( )
2.已知关于x的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标是 .
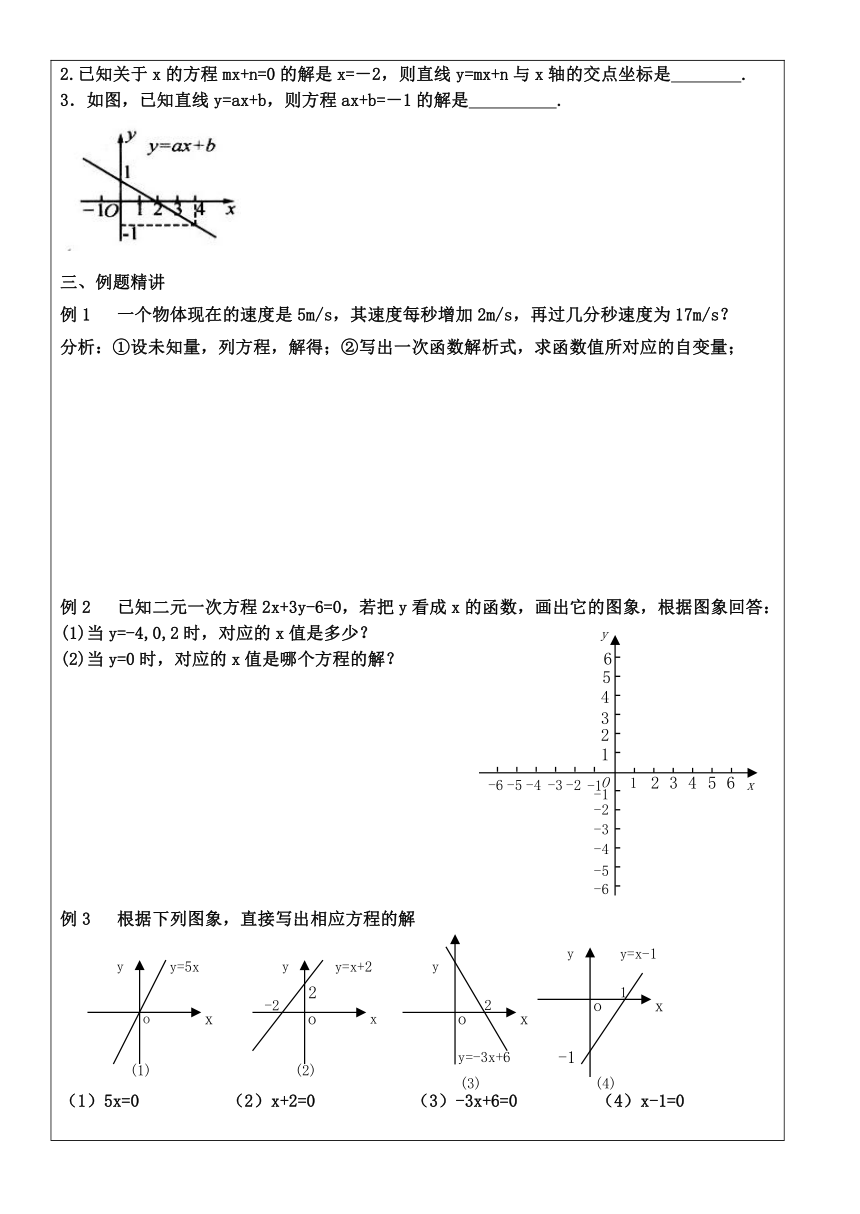
3.如图,已知直线y=ax+b,则方程ax+b=-1的解是 .
三、例题精讲
例1 一个物体现在的速度是5m/s,其速度每秒增加2m/s,再过几分秒速度为17m/s?
分析:①设未知量,列方程,解得;②写出一次函数解析式,求函数值所对应的自变量;
例2 已知二元一次方程2x+3y-6=0,若把y看成x的函数,画出它的图象,根据图象回答:
(1)当y=-4,0,2时,对应的x值是多少?
(2)当y=0时,对应的x值是哪个方程的解?
例3 根据下列图象,直接写出相应方程的解
(1)5x=0 (2)x+2=0 (3)-3x+6=0 (4)x-1=0
四、当堂达标
1.(4分)若方程x-3=0的解也是直线y=(4k+1)x-15与x轴的交点的横坐标,则k的值为( )
A.-1 B.0 C.1 D.±1
2.(4分)一次函数的图象经过点A(-2,-1),且与直线y=2x-3平行,则此函数与x轴交点坐标为( )
A.(-) B.(-2,0) C.(-1,0) D.()
3.(4分)已知一次函数y=kx+b,当x=1时,y=2,且图象与y轴交点纵坐标是3,则方程kx+b=0解为( )
A.x=-3 B.x=-1 C.x=1 D.x=3
4.(8分)利用图象求方程3x-1=x+1的解 ,并笔算验证。
B 2.(-2,0) 3.x=4
例1 解法1:设再过x秒物体的速度为17 m/s.
由题意得 2x+5=17
解得 x=6
答:再过 6 秒物体的速度为17m/s.
解法2:速度y(m/s)是时间t(s)的函数,
关系式是 y=2x+5
当y=17时,2x+5=17
解得 x=6
答:再过 6 秒物体的速度为17m/s.
解法3:设再过x秒物体的速度为17 m/s.
由题意得 2x+5=17
变形得 2x-12=0
由图象可得直线 y=2x-12
与x轴的交点为(6,0).
即: x=6
答:再过 6 秒物体的速度为17m/s.
例2 (1)图象略,-4,0,2;(2)3
例3 x=0 ,x=-2 ,x=2 ,x=1
1.C 2.A 3.D
4.解法一:直线y=2x-2与x轴交点为(1,0);解法二:由图象可以看出直线y=3x-1与y=x+1交于点(1,2),所以x=1 .
课题 19.2.3一次函数与一元一次方程 课型 新授
学习 目标 1、理解一次函数与一元一次方程的关系。
2、会根据一次函数的图像解决一元一次方程的求解。
学习 关键 重点 1、理解一次函数与一元一次方程的关系。
2、会根据一次函数的图像解决一元一次方程的求解。
难点 一次函数与一元一次方程的关系的发现、归纳、和运用
学教过程
探究新知 1.问题1:解方程2x+20=0 它的解为 。
问题2:自变量x为何值时,函数y=2x+20的值为0?
联想:问题(1),(2)是同一个问题吗?
问题3:画出直线y=2x+20的图像,并确定它与x轴交点的坐标。
2、知识点的归纳总结:
由于任何一元一次方程都可以转化为 的形式,所以解一元一次方程可以转化为求一次函数 函数值为0时的相应的自变量的值。
从图像上看,这又相当于求直线y= 与 轴交点的横坐标。
简言之:求一元一次方程的解就是求一次函数与x轴交点的横坐标。
二、巩固练习
1.已知方程ax+b=0的解是-2,下列图象肯定不是直线 y=ax+b的是( )
2.已知关于x的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标是 .
3.如图,已知直线y=ax+b,则方程ax+b=-1的解是 .
三、例题精讲
例1 一个物体现在的速度是5m/s,其速度每秒增加2m/s,再过几分秒速度为17m/s?
分析:①设未知量,列方程,解得;②写出一次函数解析式,求函数值所对应的自变量;
例2 已知二元一次方程2x+3y-6=0,若把y看成x的函数,画出它的图象,根据图象回答:
(1)当y=-4,0,2时,对应的x值是多少?
(2)当y=0时,对应的x值是哪个方程的解?
例3 根据下列图象,直接写出相应方程的解
(1)5x=0 (2)x+2=0 (3)-3x+6=0 (4)x-1=0
四、当堂达标
1.(4分)若方程x-3=0的解也是直线y=(4k+1)x-15与x轴的交点的横坐标,则k的值为( )
A.-1 B.0 C.1 D.±1
2.(4分)一次函数的图象经过点A(-2,-1),且与直线y=2x-3平行,则此函数与x轴交点坐标为( )
A.(-) B.(-2,0) C.(-1,0) D.()
3.(4分)已知一次函数y=kx+b,当x=1时,y=2,且图象与y轴交点纵坐标是3,则方程kx+b=0解为( )
A.x=-3 B.x=-1 C.x=1 D.x=3
4.(8分)利用图象求方程3x-1=x+1的解 ,并笔算验证。
B 2.(-2,0) 3.x=4
例1 解法1:设再过x秒物体的速度为17 m/s.
由题意得 2x+5=17
解得 x=6
答:再过 6 秒物体的速度为17m/s.
解法2:速度y(m/s)是时间t(s)的函数,
关系式是 y=2x+5
当y=17时,2x+5=17
解得 x=6
答:再过 6 秒物体的速度为17m/s.
解法3:设再过x秒物体的速度为17 m/s.
由题意得 2x+5=17
变形得 2x-12=0
由图象可得直线 y=2x-12
与x轴的交点为(6,0).
即: x=6
答:再过 6 秒物体的速度为17m/s.
例2 (1)图象略,-4,0,2;(2)3
例3 x=0 ,x=-2 ,x=2 ,x=1
1.C 2.A 3.D
4.解法一:直线y=2x-2与x轴交点为(1,0);解法二:由图象可以看出直线y=3x-1与y=x+1交于点(1,2),所以x=1 .
