19.3选择方案1-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 19.3选择方案1-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览

文档简介
授课人 年级 八 学科 数学 授课时间
课题 19.3选择方案1 课型 新授
学习 目标 1、会用一次函数知识解决方案选择问题。
2、体会如何运用一次函数选择最佳方案。
学习 关键 重点 会用一次函数知识解决方案选择问题
难点 会用一次函数知识解决方案选择问题
学教过程
探究新知 问题1:怎样选取上网收费方式
下表给出A,B,C 三种上宽带网的收费方式:
收费方式
月使用费/元
包时上网时间/小时
超时费元/分钟
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选取哪种方式能节省上网费?该问题要我们做什么?选择方案的依据是什么?
分析 :要比较三种收费方式的费用,需要做什么? 分别计算每种方案的费用.怎样计算费用?
(1)费用=月使用费+超时费, 超时费=超时使用价格×超时时间
(2)A,B,C 三种方案中,所需要的费用是固定的还是变化的?
(3)请分别写出三种方案的上网费用y元与上网时间t h之间的函数解析式.方案A,B,C的上网费用分别为y1 元,y2 元, y3 元。
(4)请比较y1,y2,y3的大小.
当上网时间_________________时,选择方式A最省钱.
当上网时间_________________时,选择方式B最省钱.
当上网时间_________________时,选择方式C最省钱.
二、例题精讲
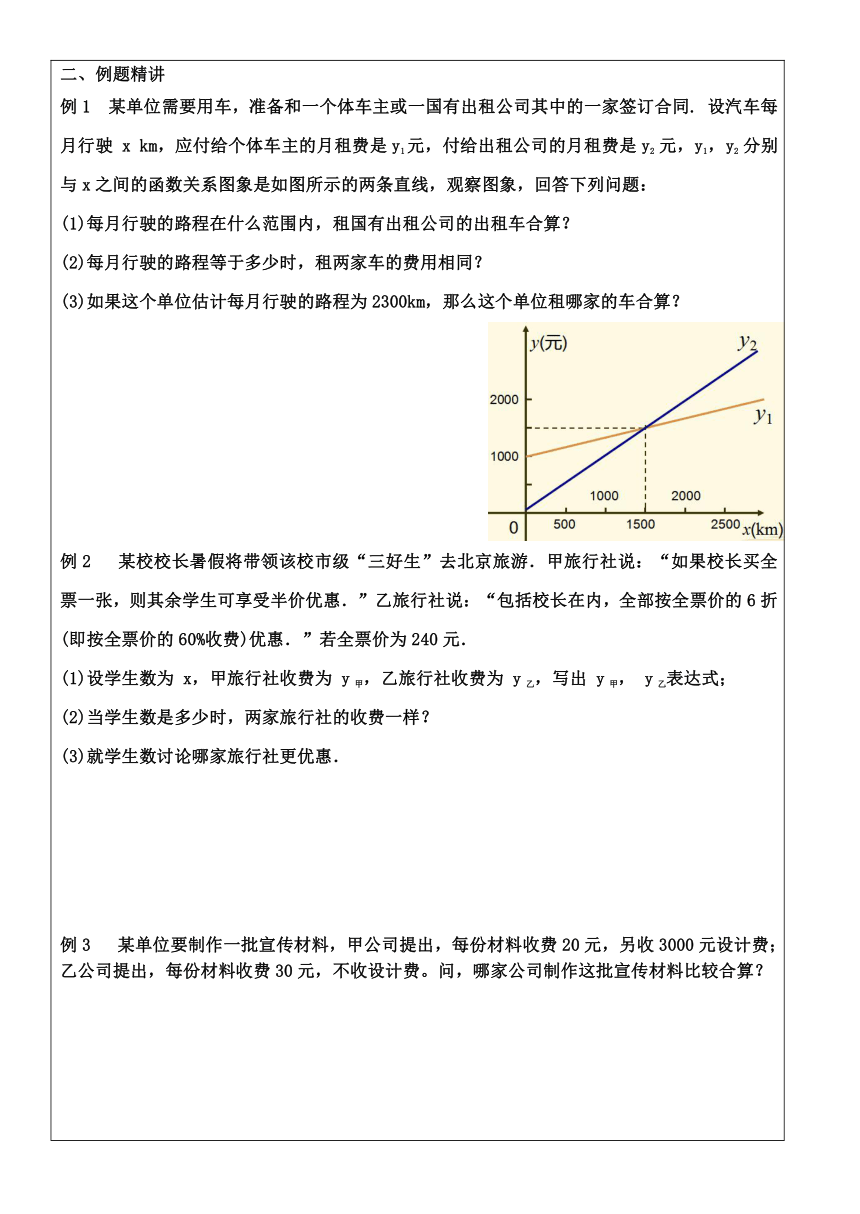
例1 某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同. 设汽车每月行驶 x km,应付给个体车主的月租费是y1元,付给出租公司的月租费是y2 元,y1,y2 分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
例2 某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.
(1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,写出 y甲, y乙表达式;
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
例3 某单位要制作一批宣传材料,甲公司提出,每份材料收费20元,另收3000元设计费;乙公司提出,每份材料收费30元,不收设计费。问,哪家公司制作这批宣传材料比较合算?
三、当堂达标
1.(4分)如图是甲、乙两家商店销售同一种产品的销售价y(单位:元)与销售量x(单位:件)之间的函数图象.下列说法:①买2件时甲、乙两家的售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买1件乙家的售价为3元.其中正确的是( )
A.①② B.①②③ C.②③ D.②③④
2.(4分)某电信局收取网费如下:163网费为每小时3元;169网费为每小时2元,但要收取每月基本费15元.设每月上网总费用为y元,上网时间为x小时.如果一个网民每月上网19小时,他应选择__________.(填“163网费”或“169网费”)
3.(8分)为庆祝商都正式营业,商都推出了两种购物方案.
方案一:非会员购物,所有商品价格可获九五折优惠;
方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5 880元的电视机一台,请分析选择哪种方案更省钱?
例1 (1)当0<x<1500时,租国有的合算.
(2)当x=1500时,租两家的费用一样.
(3)租个体车主的车合算.
例2 (1),
(2)当x = 4时,两家旅行社的收费一样.
(3)当x < 4时,乙旅行社优惠;当x > 4时,甲旅行社优惠.
例3 ,;
当x < 300时,乙公司优惠;当x > 300时,甲公司优惠,当x=300时,甲、乙公司收费一样。
1.B 2.169网费
3.(1)方案一:y=0.95x;
方案二:y=0.9x+300.
(2)∵0.95×5 880=5 586(元),0.9×5 880+300=5 592(元),
∴选择方案一更省钱.
课题 19.3选择方案1 课型 新授
学习 目标 1、会用一次函数知识解决方案选择问题。
2、体会如何运用一次函数选择最佳方案。
学习 关键 重点 会用一次函数知识解决方案选择问题
难点 会用一次函数知识解决方案选择问题
学教过程
探究新知 问题1:怎样选取上网收费方式
下表给出A,B,C 三种上宽带网的收费方式:
收费方式
月使用费/元
包时上网时间/小时
超时费元/分钟
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选取哪种方式能节省上网费?该问题要我们做什么?选择方案的依据是什么?
分析 :要比较三种收费方式的费用,需要做什么? 分别计算每种方案的费用.怎样计算费用?
(1)费用=月使用费+超时费, 超时费=超时使用价格×超时时间
(2)A,B,C 三种方案中,所需要的费用是固定的还是变化的?
(3)请分别写出三种方案的上网费用y元与上网时间t h之间的函数解析式.方案A,B,C的上网费用分别为y1 元,y2 元, y3 元。
(4)请比较y1,y2,y3的大小.
当上网时间_________________时,选择方式A最省钱.
当上网时间_________________时,选择方式B最省钱.
当上网时间_________________时,选择方式C最省钱.
二、例题精讲
例1 某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同. 设汽车每月行驶 x km,应付给个体车主的月租费是y1元,付给出租公司的月租费是y2 元,y1,y2 分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内,租国有出租公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
例2 某校校长暑假将带领该校市级“三好生”去北京旅游.甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按全票价的6折(即按全票价的60%收费)优惠.”若全票价为240元.
(1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,写出 y甲, y乙表达式;
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数讨论哪家旅行社更优惠.
例3 某单位要制作一批宣传材料,甲公司提出,每份材料收费20元,另收3000元设计费;乙公司提出,每份材料收费30元,不收设计费。问,哪家公司制作这批宣传材料比较合算?
三、当堂达标
1.(4分)如图是甲、乙两家商店销售同一种产品的销售价y(单位:元)与销售量x(单位:件)之间的函数图象.下列说法:①买2件时甲、乙两家的售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买1件乙家的售价为3元.其中正确的是( )
A.①② B.①②③ C.②③ D.②③④
2.(4分)某电信局收取网费如下:163网费为每小时3元;169网费为每小时2元,但要收取每月基本费15元.设每月上网总费用为y元,上网时间为x小时.如果一个网民每月上网19小时,他应选择__________.(填“163网费”或“169网费”)
3.(8分)为庆祝商都正式营业,商都推出了两种购物方案.
方案一:非会员购物,所有商品价格可获九五折优惠;
方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5 880元的电视机一台,请分析选择哪种方案更省钱?
例1 (1)当0<x<1500时,租国有的合算.
(2)当x=1500时,租两家的费用一样.
(3)租个体车主的车合算.
例2 (1),
(2)当x = 4时,两家旅行社的收费一样.
(3)当x < 4时,乙旅行社优惠;当x > 4时,甲旅行社优惠.
例3 ,;
当x < 300时,乙公司优惠;当x > 300时,甲公司优惠,当x=300时,甲、乙公司收费一样。
1.B 2.169网费
3.(1)方案一:y=0.95x;
方案二:y=0.9x+300.
(2)∵0.95×5 880=5 586(元),0.9×5 880+300=5 592(元),
∴选择方案一更省钱.
