2020-2021学年鲁教版(五四制)数学六年级下册期末综合复习模拟测试题1(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教版(五四制)数学六年级下册期末综合复习模拟测试题1(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 16:06:44 | ||
图片预览




文档简介
2020-2021学年鲁教版六年级数学期末综合复习模拟测试题1(附答案)
一、选择题(共10小题,每题3分,共计30分)
1.钟表上12时15分时,时针和分针的夹角是( )
A.60° B.82.5° C.90° D.120°
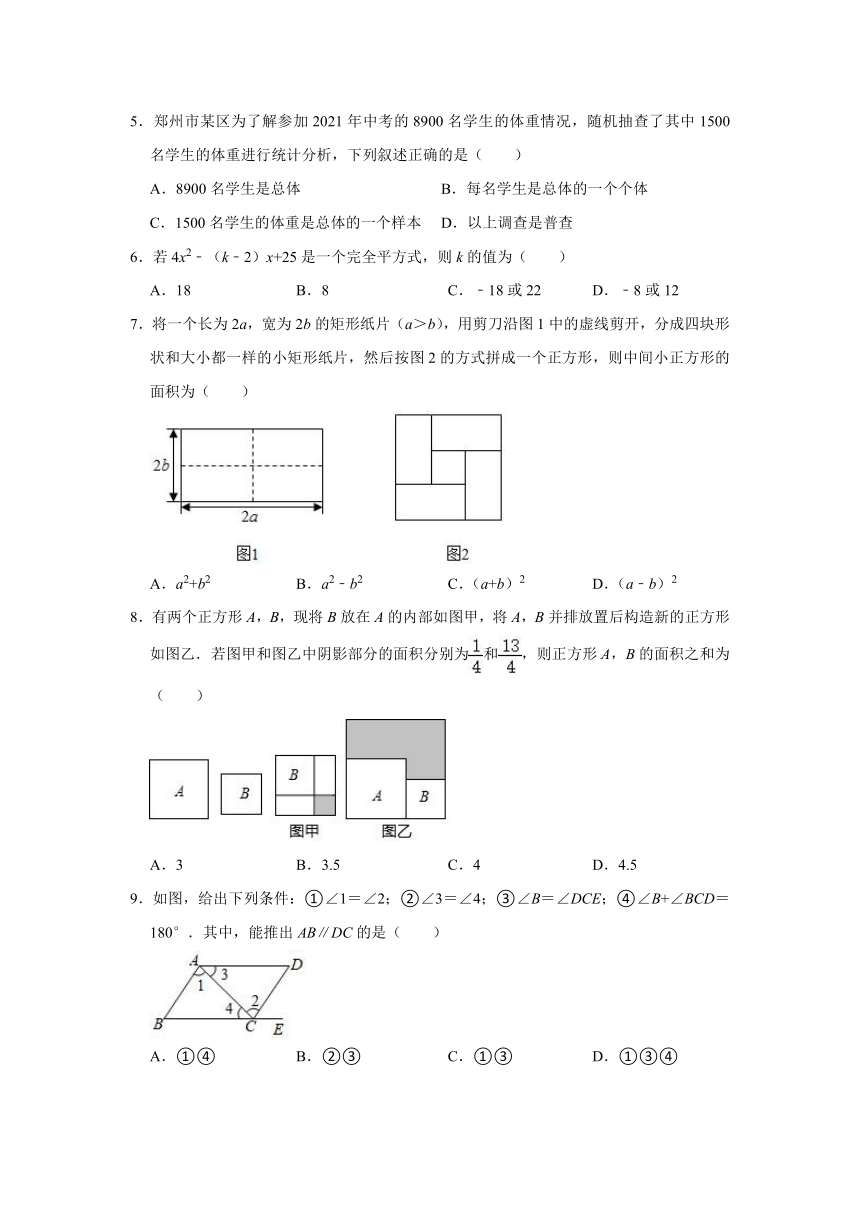
2.如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75° B.60° C.65° D.55°
3.某校为了解学生的出行方式,通过调查制作了如图所示的条形统计图,由图可知,下列说法错误的是( )
A.步行的人数最少
B.骑自行车的人数为90
C.步行与骑自行车的总人数比坐公共汽车的人数要多
D.坐公共汽车的人数占总人数的50%
4.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.两车到第3秒时行驶的路程相同
B.在0到8秒内甲的速度每秒增加4米
C.乙前4秒行驶的路程为48米
D.在4到8秒内乙的速度都小于甲的速度
5.郑州市某区为了解参加2021年中考的8900名学生的体重情况,随机抽查了其中1500名学生的体重进行统计分析,下列叙述正确的是( )
A.8900名学生是总体 B.每名学生是总体的一个个体
C.1500名学生的体重是总体的一个样本 D.以上调查是普查
6.若4x2﹣(k﹣2)x+25是一个完全平方式,则k的值为( )
A.18 B.8 C.﹣18或22 D.﹣8或12
7.将一个长为2a,宽为2b的矩形纸片(a>b),用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为( )
A.a2+b2 B.a2﹣b2 C.(a+b)2 D.(a﹣b)2
8.有两个正方形A,B,现将B放在A的内部如图甲,将A,B并排放置后构造新的正方形如图乙.若图甲和图乙中阴影部分的面积分别为和,则正方形A,B的面积之和为( )
A.3 B.3.5 C.4 D.4.5
9.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BCD=180°.其中,能推出AB∥DC的是( )
A.①④ B.②③ C.①③ D.①③④
10.如图,已知直线a∥b,则∠1、∠2、∠3的关系是( )
A.∠1+∠2+∠3=360° B.∠1+∠2﹣∠3=180°
C.∠1﹣∠2+∠3=180° D.∠1+∠2+∠3=180°
二、填空题(共10小题,每题3分,共计30分)
11.已知,∠AOB=50°,∠BOC=30°,OD是∠AOC的角平分线,则∠DOB的度数是 .
12.已知点D为线段AB的中点,且在直线AB上有一点C,AB=4BC,若CD=6cm,则AB的长为 cm.
13.某住宅小区5月1日~5月5日每天用水量变化情况如图所示,则2日到3日的每天用水量的增长率为 .
14.若某地打长途电话3分钟之内收费1.8元,每增加1分钟加收0.5元,当通话时间为t分钟时(t≥3且t为整数),电话费y(元)与通话时间t(分)之间的关系式为 .
15.端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离S(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是 点.
16.若(1﹣x)2﹣3x=1,则x= .
17.已知x2+y2=39,x﹣y=3,则(x+y)2的值 .
18.(﹣)2020?(1.5)2021= .
19.计算:2022×2020﹣20212的结果为 .
20.图1是一盏可折叠台灯.图2为其平面示意图,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠A是∠B的两倍,灯体CD可绕点C旋转调节.现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示),此时,灯体CD′所在的直线恰好垂直支架AB,且∠BCD﹣∠DCD′=126°,则∠DCD′= .
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.先化简,再求值:
(1)已知:x+2y+1=3,求3x×9y×3的值.
(2)已知:x2m=3,y2n=5,求(x3m)2+(﹣y3n)2﹣xm﹣1yn?xm+1yn的值.
22.已知:|a﹣b﹣1|+a2﹣4a+4=0,化简求值:[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a).
23.如图①,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm.
(1)求线段AB的长;
(2)如图②,若M,N分别为AD,CB的中点,求线段MN的长;
(3)类比以上探究,如图③,解决以下问题:射线OA,OB分别为∠MOP和∠NOP的平分线,∠MON=α,∠NOP=β(β<α).求∠AOB的大小.
24.为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2700名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?
25.小明家距离学校8千米.一天早晨,小明骑车上学途中自行车出现故障,他于原地修车,车修好后,立即在确保安全的前提下以更快的速度匀速骑行到达学校.如图反映的是小明上学过程中骑行的路程(千米)与他所用的时间(分钟)之间的关系,请根据图象,解答下列问题:
(1)小明骑行了 千米时,自行车出现故障;修车用了 分钟;
(2)自行车出现故障前小明骑行的平均速度为 千米/分,修好车后骑行的平均速度为 千米/分;
(3)若自行车不发生故障,小明一直按故障前的速度匀速骑行,与他实际所用时间相比,将早到或晚到学校多少分钟?
26.如图,∠1+∠2=180°,∠3=∠B.求证:DE∥BC.
27.如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.
(1)用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式;
(2)选取1张A型卡片,10张C型卡片, 张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为 ;
(3)如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.
28.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
参考答案
一、选择题(共10小题,每题3分,共计30分)
1.解:∵时针在钟面上每分钟转0.5°,分针每分钟转6°,
∴钟表上12时15分钟时,时针与分针的夹角可以看成时针转过12时0.5°×15=7.5°,分针在数字3上.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴12时15分钟时分针与时针的夹角90°﹣7.5°=82.5°.
故选:B.
2.解:∵∠AOB=90°,∠BOC=15°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣15°=75°,
∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×75°=150°,
∴∠BOD=∠AOD﹣∠AOB=150°﹣90°=60°.
故选:B.
3.解:由条形统计图可知,出行方式中步行的有60人,骑自行车的有90人,乘公共汽车的有150人,
因此得出的总人数为60+90+150=300(人),乘公共汽车占×100%=50%,60+90=150(人),
所以选项A、B、D都是正确的,因此不符合题意;
选项C是不正确的,因此符合题意;
故选:C.
4.解:A.由于甲的图象是过原点的直线,所以可得v=4t(v、t分别表示速度、时间),
将v=12m/s代入v=4t得t=3s,则t=3s前,甲的速度小于乙的速度,所以两车到第3秒时行驶的路程不相等,符合题意;
B.根据图象得:在0到8秒内甲的速度是一条过原点的直线,即甲的速度从0均匀增加到32米/秒,则每秒增加(32÷8)=4(米/秒),不符合题意;
C.根据图象可得,乙前4秒的速度不变,为12米/秒,则行驶的路程为12×4=48米,不符合题意;
D.在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,不符合题意.
故选:A.
5.解:“8900名学生的体重情况”是考查的总体,因此选项A不符合题意;
“每一名学生的体重情况”是总体的一个个体,因此选项B不符合题意;
“1500名学生的体重情况”是总体的一个样本,因此选项C符合题意;
以上调查是抽样调查,不是普查,因此选项D不符合题意;
故选:C.
6.解:∵4x2﹣(k﹣2)x+25是一个完全平方式,
∴k﹣2=±20,
解得:k=22或k=﹣18,
故选:C.
7.解:中间空的部分的面积=大正方形的面积﹣4个小长方形的面积,
=(a+b)2﹣4ab,
=a2+2ab+b2﹣4ab,
=(a﹣b)2;
故选:D.
8.解:设A的边长为x,B的边长为y,
由甲、乙阴影面积分别是、可列方程组,
将②化简得2xy=③,
由①得,将③代入可知x2+y2=3.5.
故选:B.
9.解:①∵∠1=∠2,
∴AB∥DC,本选项符合题意;
②∵∠3=∠4,
∴AD∥CB,本选项不符合题意;
③∵∠B=∠DCE,
∴AB∥CD,本选项符合题意;
④∵∠B+∠BCD=180°,
∴AB∥CD,本选项不符合题意.
则符合题意的选项为①③④.
故选:D.
10.解:如图,过A作AB∥a,
∵a∥b,
∴AB∥b,
∴∠1+∠BAD=180°,∠2=∠BAC=∠3+∠BAD,
∴∠BAD=∠2﹣∠3,
∴∠1+∠2﹣∠3=180°,
故选:B.
二、填空题(共10小题,每题3分,共计30分)
11.解:当∠BOC在∠AOB外部时,如图所示,
则∠AOC=50°+30°=80°.
∵OD是∠AOC的角平分线,
∴∠AOD=∠COD=40°,
∴∠BOD=∠AOB﹣∠AOD=50°﹣40°=10°;
当∠BOC在∠AOB内部时,如图所示,
则∠AOC=50°﹣30°=20°.
∵OD是∠AOC的角平分线,
∴∠AOD=∠COD=10°,
∴∠BOD=∠COB+∠COD=30°+10°=40°.
故答案为:40°或10°.
12.解:如图,
①当C在AB的延长线上时,设BC=a,则AB=4a,AD=DB=2a,CD=3a,
∵CD=6,
∴3a=6,
∴a=2,
∴AB=8cm.
②当C′在线段AB上时,设C′B=a,则AB=4a,AD=DB=2a,DC′=a,
∵DC′=6,
∴a=6,
∴AB=24cm.
综上所述,AB的长为8或24cm,
故答案为8或24.
13.解:由图可得,2日用水量20立方米,3日用水量是24立方米,
则2日到3日的每天用水量的增长率为(24﹣20)÷20=20%.
故答案为:20%.
14.解:由题意得,y=1.8+0.5(t﹣3)=0.5t+0.3,
故答案为:y=0.5t+0.3.
15.解:由图象可得,景点离小明家180千米;
小明从景点回家的行驶速度为:(千米/时),
所以小明一家开车回到家的时间是:14+180÷60=17(时).
故答案为:17.
16.解:∵(1﹣x)2﹣3x=1,
①当2﹣3x=0,x=;
②当1﹣x=1,即x=0时,2﹣3x=2,12=1;
③当1﹣x=﹣1,即x=2时,2﹣3x=﹣4,(﹣1 )﹣4=1.
∴x=或0或2.
故答案为或0或2.
17.解:∵x﹣y=3,
∴(x﹣y)2=9,即x2﹣2xy+y2=9,
∵x2+y2=39,
∴39﹣2xy=9,
∴2xy=30,
∴(x+y)2=x2+2xy+y2=39+30=69.
故答案为69.
18.解:(﹣)2020?(1.5)2021
=(﹣)2020?(1.5)2020×
=(﹣)2020?()2020×
=
=
=
=.
故答案为:.
19.解:原式=(2021+1)(2021﹣1)﹣20212=20212﹣1﹣20212=﹣1.
故答案为:﹣1.
20.解:延长OA交CD于点F,延长D'C交AB于点G,
∵CD∥OE,
∴OA⊥CD,
∵AO⊥OE,D'C⊥AB,
∴∠AGC=∠AFC=90°,
∴∠GCF+∠GAF=180°,
∵∠DCD'+∠GCF=180°,
∴∠DCD'=∠GAF,
∴∠BAO=180°﹣∠DCD',
∴∠B=(180°﹣∠DCD'),
∵∠BCD﹣∠DCD'=126°,
∴∠BCD=∠DCD'+126°,
在四边形ABCF中,有∠GAF+∠B+∠BCD+∠AFC=360°,
∴∠DCD'+(180°﹣∠DCD')+∠DCD'+126°+90°=360°,
解得:∠DCD'=36°,
故答案为:36°.
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.解:(1)x+2y+1=3,
∴3x×9y×3=3x×32y×3=3x+2y+1=33=27;
(2)∵x2m=3,y2n=5,
∴(x3m)2+(﹣y3n)2﹣xm﹣1yn?xm+1yn=(x2m)3+(y2n)3﹣x2my2n
=33+53﹣3×5=27+125﹣15=137.
22.解:∵|a﹣b﹣1|+a2﹣4a+4=0,
∴|a﹣b﹣1|+(a﹣2)2=0,
∴a=2,b=1,
∴[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a)
=[9a2﹣12ab+4b2﹣(2a2+ab﹣6ab﹣3b2)+9a2﹣b2﹣6b2]÷(﹣a)
=(16a2﹣7ab)÷(﹣a)
=﹣48a+21b,
将a=2,b=1,代入上式可得:
原式=﹣48×2+21×1=﹣75.
23.解:(1)∵CB=4cm,DB=7cm.
∴DC=DB﹣CB=3cm.
∵D是AC的中点,
∴AC=2DC=6cm.
∴AB=AC+CB=10cm;
(2)由(1)知:AD=DC=3cm,
∵M,N分别为AD,CB的中点,
∴MD=AD=1.5cm,CN=BC=2cm,
∴MN=MD+DC+CN=1.5+3+2=6.5(cm);
(3)∵∠MON=α,∠NOP=β,
∴∠MOP=∠MON+∠NOP=α+β,
∵OA,OB分别为∠MOP和∠NOP的平分线,
∴∠AOM=∠AOP=MOP=(α+β),
∠BOP=NOP=,
∴∠AOB=∠AOP﹣∠BOP=(α+β)﹣=.
24.解:(1)∵被调查的总人数为10÷=50(人),
∴D等级人数所占百分比a%=×100%=30%,即a=30,
C等级人数为50﹣(5+7+15+10)=13人,
补全图形如下:
故答案为:30;
(2)扇形B的圆心角度数为360°×=50.4°;
(3)估计获得优秀奖的学生有2700×=540(人).
25.解:(1)由图可知,小明行了3千米时,自行车出现故障,
修车用了15﹣10=5(分钟);
故答案为:3;5;
(2)修车前速度:3÷10=0.3(千米/分),
修车后速度:5÷15=(千米/分);
故答案为:0.3;;
(3)8÷(分种),
30﹣=(分钟),
故他比实际情况早到分钟.
26.证明:∵∠1+∠2=180°(已知),∠2+∠ADC=180°(平角定义),
∴∠1=∠ADC,
∴EF∥AB(同位角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠ADE=∠B,
∴DE∥BC(同位角相等,两直线平行).
27.解:(1)方法1:大正方形的面积为(a+b)2,
方法2:图2中四部分的面积和为:a2+2ab+b2,
因此有(a+b)2=a2+2ab+b2,
(2)由面积拼图可知a2+10ab+25b2=(a+5b)2,
故答案为:25,(a+5b),
(3)由图形面积之间的关系可得,
S阴影=m2﹣n(m﹣n)
=m2﹣mn+n2
=[(m+n)2﹣3mn]
=(102﹣3×19)
=.
28.解:
(1)如图1,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠A+∠AOB=90°,
∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,
∴∠DBG=90°,
∴∠ABD+∠ABG=90°,
∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)知∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,
则∠ABE=α,∠ABD=2α=∠CBG,
∠GBF=∠AFB=β,
∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°得:
2α+β+3α+3α+β=180°,
∵AB⊥BC,
∴β+β+2α=90°,
∴α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
一、选择题(共10小题,每题3分,共计30分)
1.钟表上12时15分时,时针和分针的夹角是( )
A.60° B.82.5° C.90° D.120°
2.如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75° B.60° C.65° D.55°
3.某校为了解学生的出行方式,通过调查制作了如图所示的条形统计图,由图可知,下列说法错误的是( )
A.步行的人数最少
B.骑自行车的人数为90
C.步行与骑自行车的总人数比坐公共汽车的人数要多
D.坐公共汽车的人数占总人数的50%
4.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.两车到第3秒时行驶的路程相同
B.在0到8秒内甲的速度每秒增加4米
C.乙前4秒行驶的路程为48米
D.在4到8秒内乙的速度都小于甲的速度
5.郑州市某区为了解参加2021年中考的8900名学生的体重情况,随机抽查了其中1500名学生的体重进行统计分析,下列叙述正确的是( )
A.8900名学生是总体 B.每名学生是总体的一个个体
C.1500名学生的体重是总体的一个样本 D.以上调查是普查
6.若4x2﹣(k﹣2)x+25是一个完全平方式,则k的值为( )
A.18 B.8 C.﹣18或22 D.﹣8或12
7.将一个长为2a,宽为2b的矩形纸片(a>b),用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为( )
A.a2+b2 B.a2﹣b2 C.(a+b)2 D.(a﹣b)2
8.有两个正方形A,B,现将B放在A的内部如图甲,将A,B并排放置后构造新的正方形如图乙.若图甲和图乙中阴影部分的面积分别为和,则正方形A,B的面积之和为( )
A.3 B.3.5 C.4 D.4.5
9.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BCD=180°.其中,能推出AB∥DC的是( )
A.①④ B.②③ C.①③ D.①③④
10.如图,已知直线a∥b,则∠1、∠2、∠3的关系是( )
A.∠1+∠2+∠3=360° B.∠1+∠2﹣∠3=180°
C.∠1﹣∠2+∠3=180° D.∠1+∠2+∠3=180°
二、填空题(共10小题,每题3分,共计30分)
11.已知,∠AOB=50°,∠BOC=30°,OD是∠AOC的角平分线,则∠DOB的度数是 .
12.已知点D为线段AB的中点,且在直线AB上有一点C,AB=4BC,若CD=6cm,则AB的长为 cm.
13.某住宅小区5月1日~5月5日每天用水量变化情况如图所示,则2日到3日的每天用水量的增长率为 .
14.若某地打长途电话3分钟之内收费1.8元,每增加1分钟加收0.5元,当通话时间为t分钟时(t≥3且t为整数),电话费y(元)与通话时间t(分)之间的关系式为 .
15.端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离S(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是 点.
16.若(1﹣x)2﹣3x=1,则x= .
17.已知x2+y2=39,x﹣y=3,则(x+y)2的值 .
18.(﹣)2020?(1.5)2021= .
19.计算:2022×2020﹣20212的结果为 .
20.图1是一盏可折叠台灯.图2为其平面示意图,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠A是∠B的两倍,灯体CD可绕点C旋转调节.现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示),此时,灯体CD′所在的直线恰好垂直支架AB,且∠BCD﹣∠DCD′=126°,则∠DCD′= .
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.先化简,再求值:
(1)已知:x+2y+1=3,求3x×9y×3的值.
(2)已知:x2m=3,y2n=5,求(x3m)2+(﹣y3n)2﹣xm﹣1yn?xm+1yn的值.
22.已知:|a﹣b﹣1|+a2﹣4a+4=0,化简求值:[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a).
23.如图①,已知点C、D是线段AB上两点,D是AC的中点,若CB=4cm,DB=7cm.
(1)求线段AB的长;
(2)如图②,若M,N分别为AD,CB的中点,求线段MN的长;
(3)类比以上探究,如图③,解决以下问题:射线OA,OB分别为∠MOP和∠NOP的平分线,∠MON=α,∠NOP=β(β<α).求∠AOB的大小.
24.为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2700名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?
25.小明家距离学校8千米.一天早晨,小明骑车上学途中自行车出现故障,他于原地修车,车修好后,立即在确保安全的前提下以更快的速度匀速骑行到达学校.如图反映的是小明上学过程中骑行的路程(千米)与他所用的时间(分钟)之间的关系,请根据图象,解答下列问题:
(1)小明骑行了 千米时,自行车出现故障;修车用了 分钟;
(2)自行车出现故障前小明骑行的平均速度为 千米/分,修好车后骑行的平均速度为 千米/分;
(3)若自行车不发生故障,小明一直按故障前的速度匀速骑行,与他实际所用时间相比,将早到或晚到学校多少分钟?
26.如图,∠1+∠2=180°,∠3=∠B.求证:DE∥BC.
27.如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.
(1)用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式;
(2)选取1张A型卡片,10张C型卡片, 张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为 ;
(3)如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.
28.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
参考答案
一、选择题(共10小题,每题3分,共计30分)
1.解:∵时针在钟面上每分钟转0.5°,分针每分钟转6°,
∴钟表上12时15分钟时,时针与分针的夹角可以看成时针转过12时0.5°×15=7.5°,分针在数字3上.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴12时15分钟时分针与时针的夹角90°﹣7.5°=82.5°.
故选:B.
2.解:∵∠AOB=90°,∠BOC=15°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣15°=75°,
∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×75°=150°,
∴∠BOD=∠AOD﹣∠AOB=150°﹣90°=60°.
故选:B.
3.解:由条形统计图可知,出行方式中步行的有60人,骑自行车的有90人,乘公共汽车的有150人,
因此得出的总人数为60+90+150=300(人),乘公共汽车占×100%=50%,60+90=150(人),
所以选项A、B、D都是正确的,因此不符合题意;
选项C是不正确的,因此符合题意;
故选:C.
4.解:A.由于甲的图象是过原点的直线,所以可得v=4t(v、t分别表示速度、时间),
将v=12m/s代入v=4t得t=3s,则t=3s前,甲的速度小于乙的速度,所以两车到第3秒时行驶的路程不相等,符合题意;
B.根据图象得:在0到8秒内甲的速度是一条过原点的直线,即甲的速度从0均匀增加到32米/秒,则每秒增加(32÷8)=4(米/秒),不符合题意;
C.根据图象可得,乙前4秒的速度不变,为12米/秒,则行驶的路程为12×4=48米,不符合题意;
D.在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,不符合题意.
故选:A.
5.解:“8900名学生的体重情况”是考查的总体,因此选项A不符合题意;
“每一名学生的体重情况”是总体的一个个体,因此选项B不符合题意;
“1500名学生的体重情况”是总体的一个样本,因此选项C符合题意;
以上调查是抽样调查,不是普查,因此选项D不符合题意;
故选:C.
6.解:∵4x2﹣(k﹣2)x+25是一个完全平方式,
∴k﹣2=±20,
解得:k=22或k=﹣18,
故选:C.
7.解:中间空的部分的面积=大正方形的面积﹣4个小长方形的面积,
=(a+b)2﹣4ab,
=a2+2ab+b2﹣4ab,
=(a﹣b)2;
故选:D.
8.解:设A的边长为x,B的边长为y,
由甲、乙阴影面积分别是、可列方程组,
将②化简得2xy=③,
由①得,将③代入可知x2+y2=3.5.
故选:B.
9.解:①∵∠1=∠2,
∴AB∥DC,本选项符合题意;
②∵∠3=∠4,
∴AD∥CB,本选项不符合题意;
③∵∠B=∠DCE,
∴AB∥CD,本选项符合题意;
④∵∠B+∠BCD=180°,
∴AB∥CD,本选项不符合题意.
则符合题意的选项为①③④.
故选:D.
10.解:如图,过A作AB∥a,
∵a∥b,
∴AB∥b,
∴∠1+∠BAD=180°,∠2=∠BAC=∠3+∠BAD,
∴∠BAD=∠2﹣∠3,
∴∠1+∠2﹣∠3=180°,
故选:B.
二、填空题(共10小题,每题3分,共计30分)
11.解:当∠BOC在∠AOB外部时,如图所示,
则∠AOC=50°+30°=80°.
∵OD是∠AOC的角平分线,
∴∠AOD=∠COD=40°,
∴∠BOD=∠AOB﹣∠AOD=50°﹣40°=10°;
当∠BOC在∠AOB内部时,如图所示,
则∠AOC=50°﹣30°=20°.
∵OD是∠AOC的角平分线,
∴∠AOD=∠COD=10°,
∴∠BOD=∠COB+∠COD=30°+10°=40°.
故答案为:40°或10°.
12.解:如图,
①当C在AB的延长线上时,设BC=a,则AB=4a,AD=DB=2a,CD=3a,
∵CD=6,
∴3a=6,
∴a=2,
∴AB=8cm.
②当C′在线段AB上时,设C′B=a,则AB=4a,AD=DB=2a,DC′=a,
∵DC′=6,
∴a=6,
∴AB=24cm.
综上所述,AB的长为8或24cm,
故答案为8或24.
13.解:由图可得,2日用水量20立方米,3日用水量是24立方米,
则2日到3日的每天用水量的增长率为(24﹣20)÷20=20%.
故答案为:20%.
14.解:由题意得,y=1.8+0.5(t﹣3)=0.5t+0.3,
故答案为:y=0.5t+0.3.
15.解:由图象可得,景点离小明家180千米;
小明从景点回家的行驶速度为:(千米/时),
所以小明一家开车回到家的时间是:14+180÷60=17(时).
故答案为:17.
16.解:∵(1﹣x)2﹣3x=1,
①当2﹣3x=0,x=;
②当1﹣x=1,即x=0时,2﹣3x=2,12=1;
③当1﹣x=﹣1,即x=2时,2﹣3x=﹣4,(﹣1 )﹣4=1.
∴x=或0或2.
故答案为或0或2.
17.解:∵x﹣y=3,
∴(x﹣y)2=9,即x2﹣2xy+y2=9,
∵x2+y2=39,
∴39﹣2xy=9,
∴2xy=30,
∴(x+y)2=x2+2xy+y2=39+30=69.
故答案为69.
18.解:(﹣)2020?(1.5)2021
=(﹣)2020?(1.5)2020×
=(﹣)2020?()2020×
=
=
=
=.
故答案为:.
19.解:原式=(2021+1)(2021﹣1)﹣20212=20212﹣1﹣20212=﹣1.
故答案为:﹣1.
20.解:延长OA交CD于点F,延长D'C交AB于点G,
∵CD∥OE,
∴OA⊥CD,
∵AO⊥OE,D'C⊥AB,
∴∠AGC=∠AFC=90°,
∴∠GCF+∠GAF=180°,
∵∠DCD'+∠GCF=180°,
∴∠DCD'=∠GAF,
∴∠BAO=180°﹣∠DCD',
∴∠B=(180°﹣∠DCD'),
∵∠BCD﹣∠DCD'=126°,
∴∠BCD=∠DCD'+126°,
在四边形ABCF中,有∠GAF+∠B+∠BCD+∠AFC=360°,
∴∠DCD'+(180°﹣∠DCD')+∠DCD'+126°+90°=360°,
解得:∠DCD'=36°,
故答案为:36°.
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.解:(1)x+2y+1=3,
∴3x×9y×3=3x×32y×3=3x+2y+1=33=27;
(2)∵x2m=3,y2n=5,
∴(x3m)2+(﹣y3n)2﹣xm﹣1yn?xm+1yn=(x2m)3+(y2n)3﹣x2my2n
=33+53﹣3×5=27+125﹣15=137.
22.解:∵|a﹣b﹣1|+a2﹣4a+4=0,
∴|a﹣b﹣1|+(a﹣2)2=0,
∴a=2,b=1,
∴[(3a﹣2b)2﹣(a﹣3b)(2a+b)+(3a+b)(3a﹣b)﹣6b2]÷(﹣a)
=[9a2﹣12ab+4b2﹣(2a2+ab﹣6ab﹣3b2)+9a2﹣b2﹣6b2]÷(﹣a)
=(16a2﹣7ab)÷(﹣a)
=﹣48a+21b,
将a=2,b=1,代入上式可得:
原式=﹣48×2+21×1=﹣75.
23.解:(1)∵CB=4cm,DB=7cm.
∴DC=DB﹣CB=3cm.
∵D是AC的中点,
∴AC=2DC=6cm.
∴AB=AC+CB=10cm;
(2)由(1)知:AD=DC=3cm,
∵M,N分别为AD,CB的中点,
∴MD=AD=1.5cm,CN=BC=2cm,
∴MN=MD+DC+CN=1.5+3+2=6.5(cm);
(3)∵∠MON=α,∠NOP=β,
∴∠MOP=∠MON+∠NOP=α+β,
∵OA,OB分别为∠MOP和∠NOP的平分线,
∴∠AOM=∠AOP=MOP=(α+β),
∠BOP=NOP=,
∴∠AOB=∠AOP﹣∠BOP=(α+β)﹣=.
24.解:(1)∵被调查的总人数为10÷=50(人),
∴D等级人数所占百分比a%=×100%=30%,即a=30,
C等级人数为50﹣(5+7+15+10)=13人,
补全图形如下:
故答案为:30;
(2)扇形B的圆心角度数为360°×=50.4°;
(3)估计获得优秀奖的学生有2700×=540(人).
25.解:(1)由图可知,小明行了3千米时,自行车出现故障,
修车用了15﹣10=5(分钟);
故答案为:3;5;
(2)修车前速度:3÷10=0.3(千米/分),
修车后速度:5÷15=(千米/分);
故答案为:0.3;;
(3)8÷(分种),
30﹣=(分钟),
故他比实际情况早到分钟.
26.证明:∵∠1+∠2=180°(已知),∠2+∠ADC=180°(平角定义),
∴∠1=∠ADC,
∴EF∥AB(同位角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠ADE=∠B,
∴DE∥BC(同位角相等,两直线平行).
27.解:(1)方法1:大正方形的面积为(a+b)2,
方法2:图2中四部分的面积和为:a2+2ab+b2,
因此有(a+b)2=a2+2ab+b2,
(2)由面积拼图可知a2+10ab+25b2=(a+5b)2,
故答案为:25,(a+5b),
(3)由图形面积之间的关系可得,
S阴影=m2﹣n(m﹣n)
=m2﹣mn+n2
=[(m+n)2﹣3mn]
=(102﹣3×19)
=.
28.解:
(1)如图1,
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠A+∠AOB=90°,
∠A+∠C=90°,
故答案为:∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
∵BD⊥AM,
∴DB⊥BG,
∴∠DBG=90°,
∴∠ABD+∠ABG=90°,
∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,
∴∠C=∠CBG,
∠ABD=∠C;
(3)如图3,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)知∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,
则∠ABE=α,∠ABD=2α=∠CBG,
∠GBF=∠AFB=β,
∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°得:
2α+β+3α+3α+β=180°,
∵AB⊥BC,
∴β+β+2α=90°,
∴α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
同课章节目录
