2020-2021学年湘教版八年级数学下册期末综合复习模拟测试题1(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年湘教版八年级数学下册期末综合复习模拟测试题1(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 354.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-16 23:49:14 | ||
图片预览

文档简介
2020-2021学年湘教版八年级数学期末综合复习模拟测试题1(附答案)
一、选择题(共10小题,每题3分,共计30分)
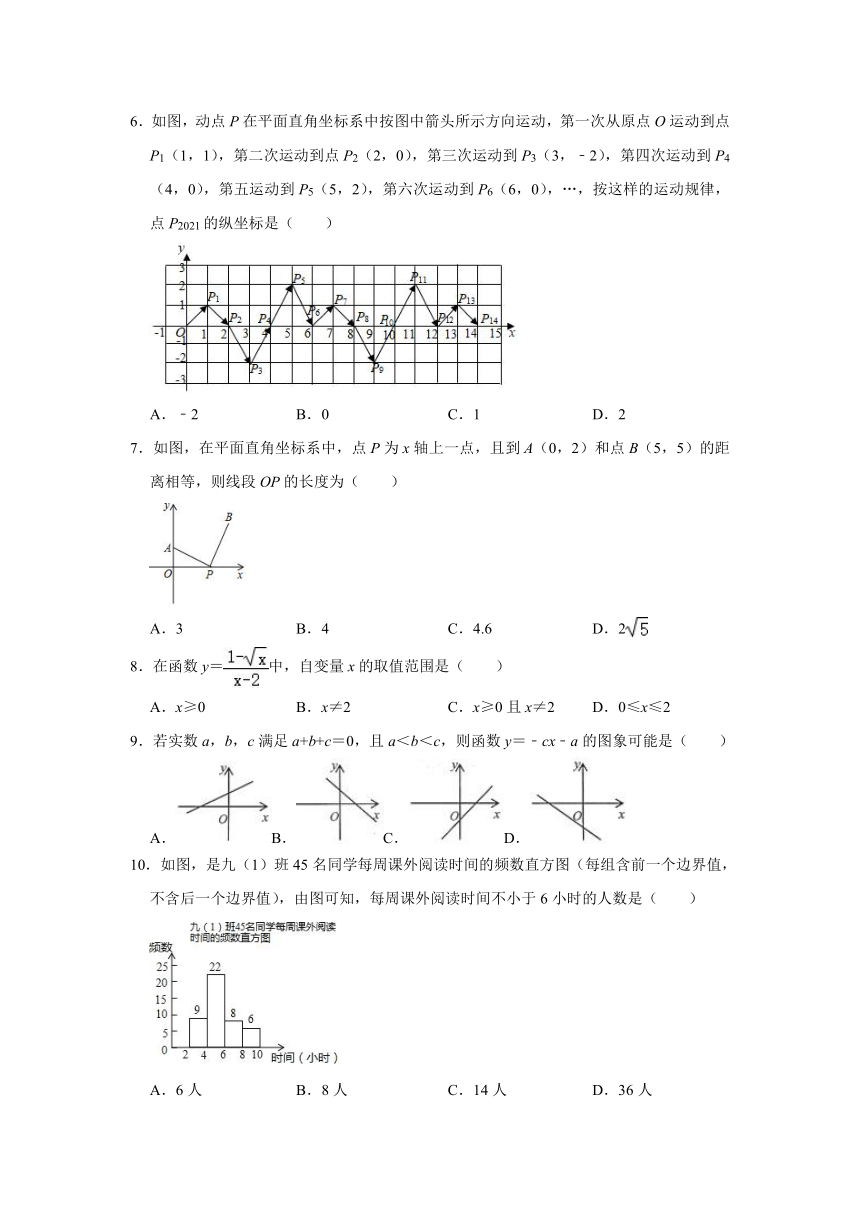
1.在Rt△ABC中,∠C=90°,AC=3,AD平分∠BAC交BC边于点D,若AD=4,则点D到AB的距离是( )
A. B. C.5 D.3
2.如图△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2 B.4 C.6 D.8
3.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a﹣b)2的值是( )
A.1 B.2 C.12 D.13
4.如图,△ABC中,∠ABC=90°,AB=4,BC=3,如果DE是△ABC的中位线,延长DE,交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.4 B.5 C.6 D.7
5.如图,线段AB的长为10,点D在AB上,△ACD是边长为3的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
A.4 B.5 C.3 D.4
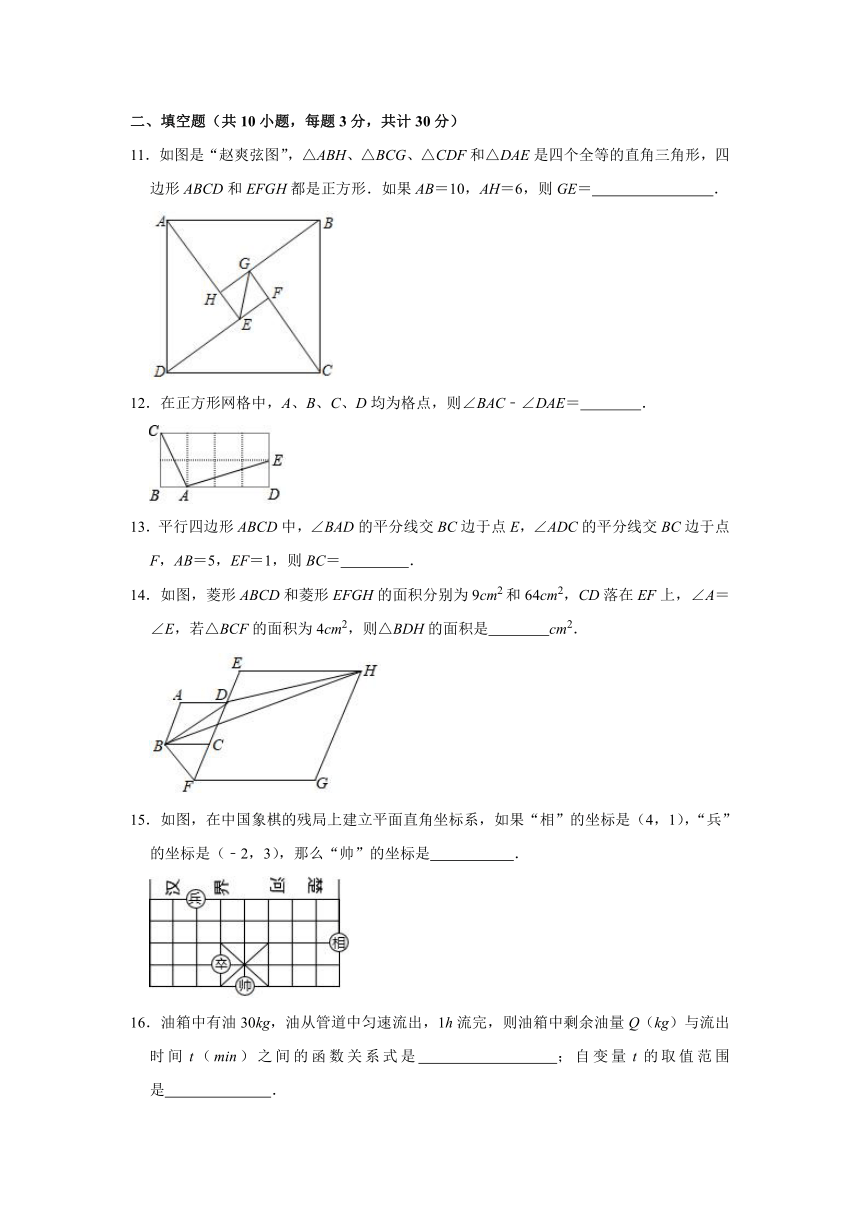
6.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
7.如图,在平面直角坐标系中,点P为x轴上一点,且到A(0,2)和点B(5,5)的距离相等,则线段OP的长度为( )
A.3 B.4 C.4.6 D.2
8.在函数y=中,自变量x的取值范围是( )
A.x≥0 B.x≠2 C.x≥0且x≠2 D.0≤x≤2
9.若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=﹣cx﹣a的图象可能是( )
A.B.C.D.
10.如图,是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值),由图可知,每周课外阅读时间不小于6小时的人数是( )
A.6人 B.8人 C.14人 D.36人
二、填空题(共10小题,每题3分,共计30分)
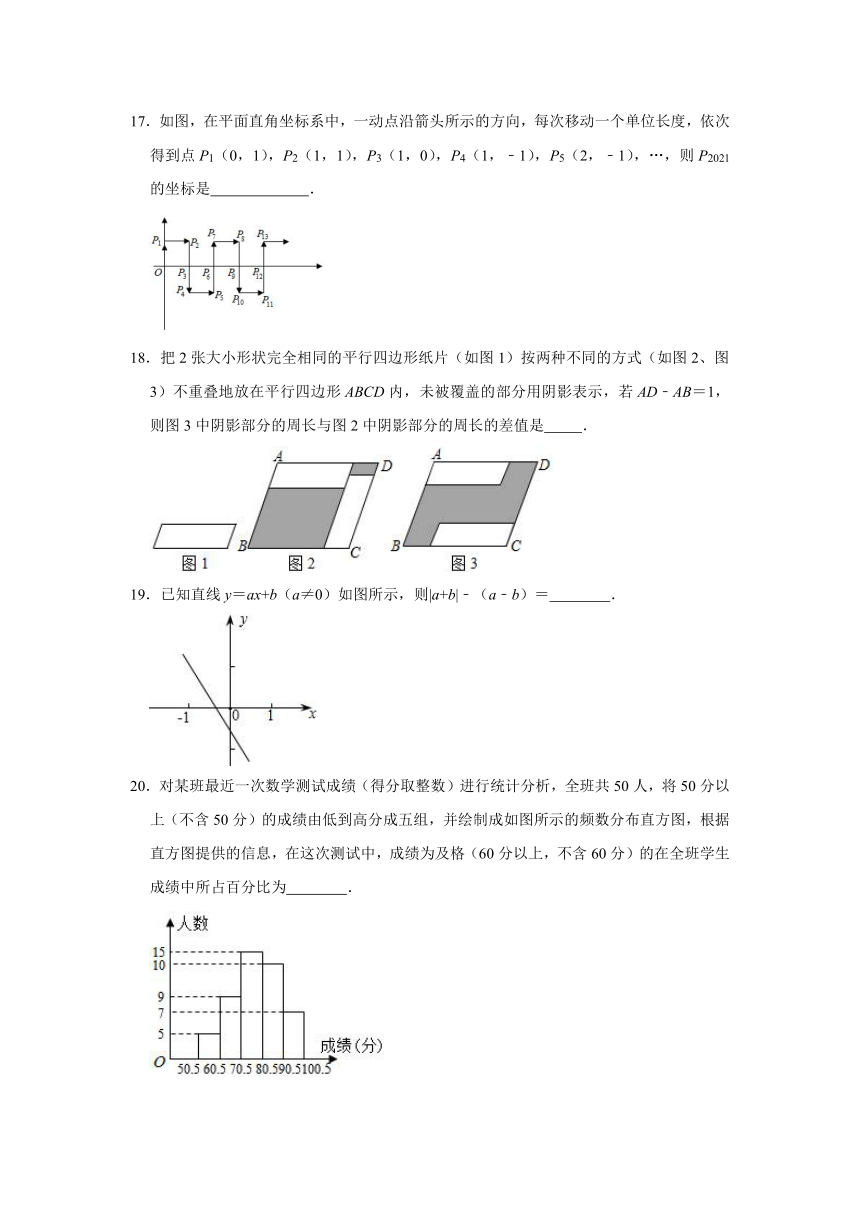
11.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,AH=6,则GE= .
12.在正方形网格中,A、B、C、D均为格点,则∠BAC﹣∠DAE= .
13.平行四边形ABCD中,∠BAD的平分线交BC边于点E,∠ADC的平分线交BC边于点F,AB=5,EF=1,则BC= .
14.如图,菱形ABCD和菱形EFGH的面积分别为9cm2和64cm2,CD落在EF上,∠A=∠E,若△BCF的面积为4cm2,则△BDH的面积是 cm2.
15.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”的坐标是(4,1),“兵”的坐标是(﹣2,3),那么“帅”的坐标是 .
16.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ;自变量t的取值范围是 .
17.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),…,则P2021的坐标是 .
18.把2张大小形状完全相同的平行四边形纸片(如图1)按两种不同的方式(如图2、图3)不重叠地放在平行四边形ABCD内,未被覆盖的部分用阴影表示,若AD﹣AB=1,则图3中阴影部分的周长与图2中阴影部分的周长的差值是 .
19.已知直线y=ax+b(a≠0)如图所示,则|a+b|﹣(a﹣b)= .
20.对某班最近一次数学测试成绩(得分取整数)进行统计分析,全班共50人,将50分以上(不含50分)的成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为及格(60分以上,不含60分)的在全班学生成绩中所占百分比为 .
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
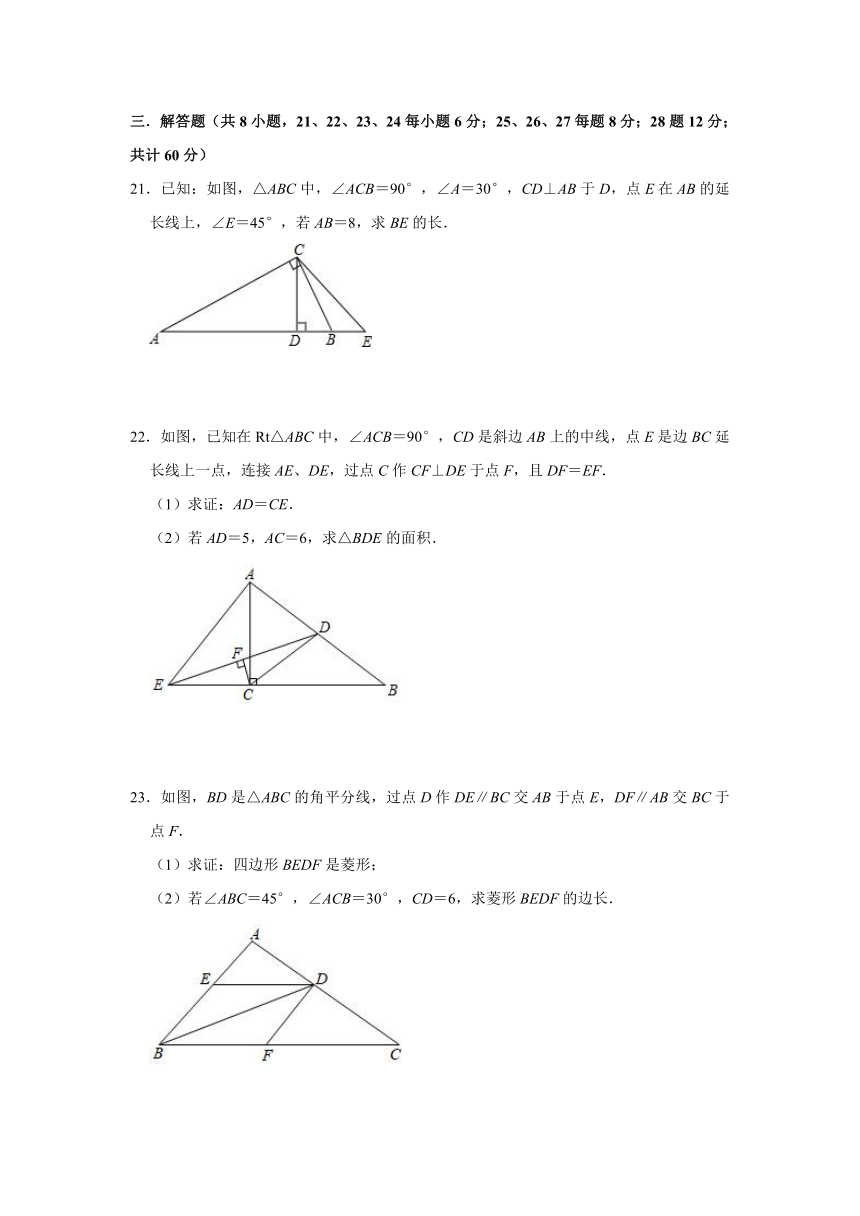
21.已知:如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,点E在AB的延长线上,∠E=45°,若AB=8,求BE的长.
22.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若AD=5,AC=6,求△BDE的面积.
23.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠ABC=45°,∠ACB=30°,CD=6,求菱形BEDF的边长.
24.如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的表达式;
(2)求△AOB的面积.
25.4月22日,垦利区九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频数和是18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)这次共抽取了多少名学生的一分钟跳绳测试成绩?
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少?
(3)请把频数分布直方图补充完整.
26.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标.
(3)求出三角形ABC的面积.
27.已知:如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,AD⊥CD,垂足为点D,M是边AB的中点,AB=20,AC=10,求线段DM的长.
28.点E在正方形AOCD的边AD上,点H在边AO上,AH=DE.
(1)如图1,求证:DH⊥CE;
(2)如图2,EF⊥CE,FH⊥AO,垂足为点H.求证:FH=AH.
参考答案
一、选择题(共10小题,每题3分,共计30分)
1.解:过点D作DE⊥AB于E,
在Rt△ADC中,∠C=90°,AC=3,AD=4,
由勾股定理得,CD===,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=,即点D到AB的距离是,
故选:B.
2.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=60°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=AB﹣AD=8﹣2=6.
故选:C.
3.解:根据勾股定理可得a2+b2=13,
四个直角三角形的面积是:ab×4=13﹣1=12,即:2ab=12
则(a﹣b)2=a2﹣2ab+b2=13﹣12=1.
方法二、小正方形的边长就是|a﹣b|,其面积是1,
故选:A.
4.解:在Rt△ABC中,AC===5,
∵DE是△ABC的中位线,
∴DE=BC=1.5,DE∥BC,EC=AC=2.5,
∴∠EFC=∠FCM,
∵CF是∠ACM的平分线,
∴∠ECF=∠FCM,
∴∠EFC=∠ECF,
∴EF=EC=2.5,
∴DF=DE+EF=1.5+2.5=4,
故选:A.
5.解:连接AO,
∵四边形CDGH是矩形,
∴CG=DH,OC=CG,OD=DH,
∴OC=OD,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
在△ACO和△ADO中,
,
∴△ACO≌△ADO(SSS),
∴∠OAB=∠CAO=30°,
∴点O一定在∠CAB的平分线上运动,
∴当OB⊥AO时,OB的长度最小,
∵∠OAB=30°,∠AOB=90°,
∴OB=AB=×10=5,
即OB的最小值为5.
故选:B.
6.解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的纵坐标是2,
故选:D.
7.解:设点P(x,0),
根据题意得,x2+22=(5﹣x)2+52,
解得:x=4.6,
∴OP=4.6,
故选:C.
8.解:根据二次根式的意义可知:x≥0.
根据分式的意义可知:x﹣2≠0,即x≠2.
∴x≥0且x≠2.
故选:C.
9.解:∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
∴﹣a>0,﹣c<0,
∴函数y=﹣cx﹣a的图象经过二、一、四象限.
故选:B.
10.解:由频数分布直方图知,每周课外阅读时间不小于6小时的人数是8+6=14(人),
故选:C.
二、填空题(共10小题,每题3分,共计30分)
11.解:∵△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,
∴AH=DE=6,AD=AB=10,
在Rt△ADE中,AE===8,
∴HE=AE﹣AH=8﹣6=2,
∵四边形EFGH是正方形,
∴GE=HE=2,
故答案为:2.
12.解:如图所示,把△ADE移到△CFG处,连接AG,
此时∠DAE=∠FCG,
∵CF∥BD,
∴∠BAC=∠FCA,
∴∠BAC﹣∠DAE=∠FCA﹣∠FCG=∠ACG,
设小正方形的边长是1,
由勾股定理得:CG2=12+32=10,AC2=AG2=12+22=5,
∴AC2+AG2=CG2,AC=AG,
∴∠CAG=90°,
即△ACG是等腰直角三角形,
∴∠ACG=45°,
∴∠BAC﹣∠DAE=45°,
故答案为:45°.
13.解:(1)如图,
∵AE平分∠BAD,DF平分∠ADC,
∴∠BAE=∠EAD,∠ADF=∠CDF,
∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∴∠BAE=∠AEB,∠DFC=∠CDF,
∴AB=BE,CD=CF,
即2AB+EF=BC,
∵AB=5,EF=1,
∴BC=11.
(2)如图,
由(1)可知:AB=BE,CD=CF,
∵AB=CD=5,
∴AB=BE=CF=5,
∵BE+CF﹣EF=BC,EF=1,
∴BC=2×5﹣1=9,
综上:BC长为11或9,
故答案为BC长为11或9.
14.解:如图,连接FH,
∵四边形ABCD是菱形,四边形EFGH是菱形,∠A=∠E,
∴∠ADC=∠EFG,∠BDC=∠ADC=∠EFH=∠EFG,△BDC的面积=×S菱形ABCD=4.5(cm2),
∴BD∥FH,
∴△BDH的面积=△BDF的面积,
∴△BDH的面积=S△BDC+S△BCF=8.5(cm2),
故答案为8.5.
15.解:如图所示:“帅”的坐标为(0,﹣1).
故答案为:(0,﹣1).
16.解:总油量减去剩余油量,得
Q=30﹣0.5t;
剩余油量为非负数,得
30﹣0.5t≥0,解得t≤60,
时间为非负数,得t≥0,
即自变量t的取值范围是0≤t≤60,
故答案为:Q=30﹣0.5t,0≤t≤60.
17.解:由图可得,P6(2,0),P12(4,0),…,P6n(2n,0),P6n+1(2n,1),
2021÷6=336???5,
∴P6×336(2×336,0),即P2016(672,0),
∴P2017(672,1),P2018(673,1),P2019(673,0),P2020(673,﹣1),P2021(674,﹣1),
故答案为:(674,﹣1).
18.解:设图1平行四边形的长边为y,短边为x,AD=m,AB=n,
∵四边形ABCD是平行四边形,
∴AB=CD=n,AD=BC=m,
∵AD﹣AB=1,
∴m﹣n=1,
∴图2中阴影部分的周长=2y+2(n﹣x)+2x+2(n﹣y)
=2y+2n﹣2x+2x+2n﹣2y
=4n,
图3中阴影部分的周长=2(n﹣x)+2y+2x+2(m﹣y)
=2n﹣2x+2y+2x+2m﹣2y
=2m+2n,
∴图3中阴影部分的周长﹣图2中阴影部分的周长=2m+2n﹣4n=2(m﹣n)=2×1=2,
故答案为:2.
19.解:根据图象可知:a<0,b<0
所以|a+b|﹣(a﹣b)=﹣a﹣b﹣a+b=﹣2a.
20.解:在这次测试中,成绩为及格(60分以上,不含60分)的在全班学生成绩中所占百分比为×100%=82%,
故答案为:82%.
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=×8=4,
∵CD⊥AB,
∴∠BCD+∠ABC=90°,
又∵∠A+∠ABC=90°,
∴∠BCD=∠A=30°,
∴BD=BC=×4=2,
在Rt△BCD中,CD===2,
∵∠E=45°,
∴∠DCE=90°﹣45°=45°,
∴∠DCE=∠E,
∴DE=CD=2,
∴BE=DE﹣BD=2﹣2.
22.(1)证明:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=AB,
∵CF⊥DE,DF=EF.
∴CE=CD,
∴AD=CE.
(2)解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,AD=5,
∴AB=2AD=10,
∵AC=6,
∴BC==8,
由(1)知,CE=CD=AD=5,
∴BE=BC+EC=13,
∴S△ABE=BE?AC=,
∵点D是AB的中点,
∴△BDE的面积=S△ABE=.
23.(1)证明:∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF,
∴∠ABD=∠EDB,
∴DE=BE,
∴平行四边形BEDF是菱形;
(2)解:过点D作DH⊥BC于H,如图所示:
由(1)得:四边形BEDF是菱形,
∴BE=DE=BF=DF,
∵DF∥AB,
∴∠ABC=∠DFC=45°,
∵DH⊥BC,
∴∠DHF=∠DHC=90°,
∴△DFH是等腰直角三角形,
∴DF=DH,
∵∠ACB=30°,CD=6,
∴DH=CD=3,
∴DF=3,
即菱形BEDF的边长为3.
24.解:(1)把A(﹣2,﹣1),B(1,3)代入y=kx+b得,
解得.
所以一次函数解析式为y=x+;
(2)把x=0代入y=x+,
得y=,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD
=××2+××1
=.
25.解:(1)∵前两组的频数和是18,第一组的人数是抽取总人数的4%,
∴抽取的总人数=(18﹣12)÷4%=150(人);
(2)∵第二、三、四组的频数比为4:17:15,第二小组的频数为12,
∴第三、四组的频数分别为:51,45,
∴第五、六小组的频数和为:150﹣(6+12+51+45)=36,
∴这次测试成绩的优秀率是:×100%=24%;
(3)频数分布直方图:
26.解:(1)点A、B、C分别在第三象限、第一象限和y轴的正半轴上,
则A(﹣2,﹣2),B(3,1),C(0,2);
(2)∵把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,
∴横坐标减1,纵坐标加2,
即A′(﹣3,0),B′(2,3),C(﹣1,4);
(3)S△ABC=4×5﹣×5×3﹣×4×2﹣×1×3
=20﹣7.5﹣4﹣1.5
=7.
27.解:延长AD交BC于E,
∵∠ACB=90°,
∴BC==10,
∵CD平分∠ACB,AD⊥CD,
∴∠ACD=∠ECD,∠ADC=∠EDC=90°,
∴∠CAD=∠CED,
∴CA=CE=10,
∴AD=DE,
∵M是边AB的中点,
∴DM=BE=×(10﹣10)=5﹣5.
28.证明:(1)∵四边形ABCD是正方形,
∴AD=CD,
∠DAH=∠CDE=90°,
在△HAD与△EDC中,
,
∴△HAD≌△EDC(SAS),
∴∠ADH=∠DCE,
∵∠ADH+∠HDC=∠DCE+∠HDC=90°,
∴∠DFC=90°,
∴CE⊥DH;
(2)如图2,过F作FG⊥AD,交DA的延长线于G,
∵FH⊥AO,
∴∠G=∠GAH=∠AHF=90°,
∴四边形AGFH是矩形,
∴FG=AH=DE,∠G=90°,
在△GFE和△DEC中,
,
∴△GFE≌△DEC(AAS),
∴EG=DC=AD,
∴EG﹣AE=AD﹣AE,
∴AG=DE=FH=AH,
∴FH=AH.
一、选择题(共10小题,每题3分,共计30分)
1.在Rt△ABC中,∠C=90°,AC=3,AD平分∠BAC交BC边于点D,若AD=4,则点D到AB的距离是( )
A. B. C.5 D.3
2.如图△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2 B.4 C.6 D.8
3.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,那么(a﹣b)2的值是( )
A.1 B.2 C.12 D.13
4.如图,△ABC中,∠ABC=90°,AB=4,BC=3,如果DE是△ABC的中位线,延长DE,交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.4 B.5 C.6 D.7
5.如图,线段AB的长为10,点D在AB上,△ACD是边长为3的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
A.4 B.5 C.3 D.4
6.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,按这样的运动规律,点P2021的纵坐标是( )
A.﹣2 B.0 C.1 D.2
7.如图,在平面直角坐标系中,点P为x轴上一点,且到A(0,2)和点B(5,5)的距离相等,则线段OP的长度为( )
A.3 B.4 C.4.6 D.2
8.在函数y=中,自变量x的取值范围是( )
A.x≥0 B.x≠2 C.x≥0且x≠2 D.0≤x≤2
9.若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=﹣cx﹣a的图象可能是( )
A.B.C.D.
10.如图,是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值),由图可知,每周课外阅读时间不小于6小时的人数是( )
A.6人 B.8人 C.14人 D.36人
二、填空题(共10小题,每题3分,共计30分)
11.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,AH=6,则GE= .
12.在正方形网格中,A、B、C、D均为格点,则∠BAC﹣∠DAE= .
13.平行四边形ABCD中,∠BAD的平分线交BC边于点E,∠ADC的平分线交BC边于点F,AB=5,EF=1,则BC= .
14.如图,菱形ABCD和菱形EFGH的面积分别为9cm2和64cm2,CD落在EF上,∠A=∠E,若△BCF的面积为4cm2,则△BDH的面积是 cm2.
15.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”的坐标是(4,1),“兵”的坐标是(﹣2,3),那么“帅”的坐标是 .
16.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ;自变量t的取值范围是 .
17.如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),…,则P2021的坐标是 .
18.把2张大小形状完全相同的平行四边形纸片(如图1)按两种不同的方式(如图2、图3)不重叠地放在平行四边形ABCD内,未被覆盖的部分用阴影表示,若AD﹣AB=1,则图3中阴影部分的周长与图2中阴影部分的周长的差值是 .
19.已知直线y=ax+b(a≠0)如图所示,则|a+b|﹣(a﹣b)= .
20.对某班最近一次数学测试成绩(得分取整数)进行统计分析,全班共50人,将50分以上(不含50分)的成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,根据直方图提供的信息,在这次测试中,成绩为及格(60分以上,不含60分)的在全班学生成绩中所占百分比为 .
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.已知:如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,点E在AB的延长线上,∠E=45°,若AB=8,求BE的长.
22.如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)求证:AD=CE.
(2)若AD=5,AC=6,求△BDE的面积.
23.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠ABC=45°,∠ACB=30°,CD=6,求菱形BEDF的边长.
24.如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的表达式;
(2)求△AOB的面积.
25.4月22日,垦利区九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频数和是18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)这次共抽取了多少名学生的一分钟跳绳测试成绩?
(2)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是多少?
(3)请把频数分布直方图补充完整.
26.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标.
(3)求出三角形ABC的面积.
27.已知:如图,在Rt△ABC中,∠ACB=90°,CD平分∠ACB,AD⊥CD,垂足为点D,M是边AB的中点,AB=20,AC=10,求线段DM的长.
28.点E在正方形AOCD的边AD上,点H在边AO上,AH=DE.
(1)如图1,求证:DH⊥CE;
(2)如图2,EF⊥CE,FH⊥AO,垂足为点H.求证:FH=AH.
参考答案
一、选择题(共10小题,每题3分,共计30分)
1.解:过点D作DE⊥AB于E,
在Rt△ADC中,∠C=90°,AC=3,AD=4,
由勾股定理得,CD===,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=,即点D到AB的距离是,
故选:B.
2.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=60°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=AB﹣AD=8﹣2=6.
故选:C.
3.解:根据勾股定理可得a2+b2=13,
四个直角三角形的面积是:ab×4=13﹣1=12,即:2ab=12
则(a﹣b)2=a2﹣2ab+b2=13﹣12=1.
方法二、小正方形的边长就是|a﹣b|,其面积是1,
故选:A.
4.解:在Rt△ABC中,AC===5,
∵DE是△ABC的中位线,
∴DE=BC=1.5,DE∥BC,EC=AC=2.5,
∴∠EFC=∠FCM,
∵CF是∠ACM的平分线,
∴∠ECF=∠FCM,
∴∠EFC=∠ECF,
∴EF=EC=2.5,
∴DF=DE+EF=1.5+2.5=4,
故选:A.
5.解:连接AO,
∵四边形CDGH是矩形,
∴CG=DH,OC=CG,OD=DH,
∴OC=OD,
∵△ACD是等边三角形,
∴AC=AD,∠CAD=60°,
在△ACO和△ADO中,
,
∴△ACO≌△ADO(SSS),
∴∠OAB=∠CAO=30°,
∴点O一定在∠CAB的平分线上运动,
∴当OB⊥AO时,OB的长度最小,
∵∠OAB=30°,∠AOB=90°,
∴OB=AB=×10=5,
即OB的最小值为5.
故选:B.
6.解:观察图象,结合动点P第一次从原点O运动到点P1(1,1),第二次运动到点P2(2,0),第三次运动到P3(3,﹣2),第四次运动到P4(4,0),第五运动到P5(5,2),第六次运动到P6(6,0),…,结合运动后的点的坐标特点,
可知由图象可得纵坐标每6次运动组成一个循环:1,0,﹣2,0,2,0;
∵2021÷6=336…5,
∴经过第2021次运动后,动点P的纵坐标是2,
故选:D.
7.解:设点P(x,0),
根据题意得,x2+22=(5﹣x)2+52,
解得:x=4.6,
∴OP=4.6,
故选:C.
8.解:根据二次根式的意义可知:x≥0.
根据分式的意义可知:x﹣2≠0,即x≠2.
∴x≥0且x≠2.
故选:C.
9.解:∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
∴﹣a>0,﹣c<0,
∴函数y=﹣cx﹣a的图象经过二、一、四象限.
故选:B.
10.解:由频数分布直方图知,每周课外阅读时间不小于6小时的人数是8+6=14(人),
故选:C.
二、填空题(共10小题,每题3分,共计30分)
11.解:∵△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,
∴AH=DE=6,AD=AB=10,
在Rt△ADE中,AE===8,
∴HE=AE﹣AH=8﹣6=2,
∵四边形EFGH是正方形,
∴GE=HE=2,
故答案为:2.
12.解:如图所示,把△ADE移到△CFG处,连接AG,
此时∠DAE=∠FCG,
∵CF∥BD,
∴∠BAC=∠FCA,
∴∠BAC﹣∠DAE=∠FCA﹣∠FCG=∠ACG,
设小正方形的边长是1,
由勾股定理得:CG2=12+32=10,AC2=AG2=12+22=5,
∴AC2+AG2=CG2,AC=AG,
∴∠CAG=90°,
即△ACG是等腰直角三角形,
∴∠ACG=45°,
∴∠BAC﹣∠DAE=45°,
故答案为:45°.
13.解:(1)如图,
∵AE平分∠BAD,DF平分∠ADC,
∴∠BAE=∠EAD,∠ADF=∠CDF,
∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∴∠BAE=∠AEB,∠DFC=∠CDF,
∴AB=BE,CD=CF,
即2AB+EF=BC,
∵AB=5,EF=1,
∴BC=11.
(2)如图,
由(1)可知:AB=BE,CD=CF,
∵AB=CD=5,
∴AB=BE=CF=5,
∵BE+CF﹣EF=BC,EF=1,
∴BC=2×5﹣1=9,
综上:BC长为11或9,
故答案为BC长为11或9.
14.解:如图,连接FH,
∵四边形ABCD是菱形,四边形EFGH是菱形,∠A=∠E,
∴∠ADC=∠EFG,∠BDC=∠ADC=∠EFH=∠EFG,△BDC的面积=×S菱形ABCD=4.5(cm2),
∴BD∥FH,
∴△BDH的面积=△BDF的面积,
∴△BDH的面积=S△BDC+S△BCF=8.5(cm2),
故答案为8.5.
15.解:如图所示:“帅”的坐标为(0,﹣1).
故答案为:(0,﹣1).
16.解:总油量减去剩余油量,得
Q=30﹣0.5t;
剩余油量为非负数,得
30﹣0.5t≥0,解得t≤60,
时间为非负数,得t≥0,
即自变量t的取值范围是0≤t≤60,
故答案为:Q=30﹣0.5t,0≤t≤60.
17.解:由图可得,P6(2,0),P12(4,0),…,P6n(2n,0),P6n+1(2n,1),
2021÷6=336???5,
∴P6×336(2×336,0),即P2016(672,0),
∴P2017(672,1),P2018(673,1),P2019(673,0),P2020(673,﹣1),P2021(674,﹣1),
故答案为:(674,﹣1).
18.解:设图1平行四边形的长边为y,短边为x,AD=m,AB=n,
∵四边形ABCD是平行四边形,
∴AB=CD=n,AD=BC=m,
∵AD﹣AB=1,
∴m﹣n=1,
∴图2中阴影部分的周长=2y+2(n﹣x)+2x+2(n﹣y)
=2y+2n﹣2x+2x+2n﹣2y
=4n,
图3中阴影部分的周长=2(n﹣x)+2y+2x+2(m﹣y)
=2n﹣2x+2y+2x+2m﹣2y
=2m+2n,
∴图3中阴影部分的周长﹣图2中阴影部分的周长=2m+2n﹣4n=2(m﹣n)=2×1=2,
故答案为:2.
19.解:根据图象可知:a<0,b<0
所以|a+b|﹣(a﹣b)=﹣a﹣b﹣a+b=﹣2a.
20.解:在这次测试中,成绩为及格(60分以上,不含60分)的在全班学生成绩中所占百分比为×100%=82%,
故答案为:82%.
三.解答题(共8小题,21、22、23、24每小题6分;25、26、27每题8分;28题12分;共计60分)
21.解:∵∠ACB=90°,∠A=30°,AB=8,
∴BC=AB=×8=4,
∵CD⊥AB,
∴∠BCD+∠ABC=90°,
又∵∠A+∠ABC=90°,
∴∠BCD=∠A=30°,
∴BD=BC=×4=2,
在Rt△BCD中,CD===2,
∵∠E=45°,
∴∠DCE=90°﹣45°=45°,
∴∠DCE=∠E,
∴DE=CD=2,
∴BE=DE﹣BD=2﹣2.
22.(1)证明:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=AB,
∵CF⊥DE,DF=EF.
∴CE=CD,
∴AD=CE.
(2)解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,AD=5,
∴AB=2AD=10,
∵AC=6,
∴BC==8,
由(1)知,CE=CD=AD=5,
∴BE=BC+EC=13,
∴S△ABE=BE?AC=,
∵点D是AB的中点,
∴△BDE的面积=S△ABE=.
23.(1)证明:∵DE∥BC,DF∥AB,
∴四边形BEDF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF,
∴∠ABD=∠EDB,
∴DE=BE,
∴平行四边形BEDF是菱形;
(2)解:过点D作DH⊥BC于H,如图所示:
由(1)得:四边形BEDF是菱形,
∴BE=DE=BF=DF,
∵DF∥AB,
∴∠ABC=∠DFC=45°,
∵DH⊥BC,
∴∠DHF=∠DHC=90°,
∴△DFH是等腰直角三角形,
∴DF=DH,
∵∠ACB=30°,CD=6,
∴DH=CD=3,
∴DF=3,
即菱形BEDF的边长为3.
24.解:(1)把A(﹣2,﹣1),B(1,3)代入y=kx+b得,
解得.
所以一次函数解析式为y=x+;
(2)把x=0代入y=x+,
得y=,
所以D点坐标为(0,),
所以△AOB的面积=S△AOD+S△BOD
=××2+××1
=.
25.解:(1)∵前两组的频数和是18,第一组的人数是抽取总人数的4%,
∴抽取的总人数=(18﹣12)÷4%=150(人);
(2)∵第二、三、四组的频数比为4:17:15,第二小组的频数为12,
∴第三、四组的频数分别为:51,45,
∴第五、六小组的频数和为:150﹣(6+12+51+45)=36,
∴这次测试成绩的优秀率是:×100%=24%;
(3)频数分布直方图:
26.解:(1)点A、B、C分别在第三象限、第一象限和y轴的正半轴上,
则A(﹣2,﹣2),B(3,1),C(0,2);
(2)∵把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,
∴横坐标减1,纵坐标加2,
即A′(﹣3,0),B′(2,3),C(﹣1,4);
(3)S△ABC=4×5﹣×5×3﹣×4×2﹣×1×3
=20﹣7.5﹣4﹣1.5
=7.
27.解:延长AD交BC于E,
∵∠ACB=90°,
∴BC==10,
∵CD平分∠ACB,AD⊥CD,
∴∠ACD=∠ECD,∠ADC=∠EDC=90°,
∴∠CAD=∠CED,
∴CA=CE=10,
∴AD=DE,
∵M是边AB的中点,
∴DM=BE=×(10﹣10)=5﹣5.
28.证明:(1)∵四边形ABCD是正方形,
∴AD=CD,
∠DAH=∠CDE=90°,
在△HAD与△EDC中,
,
∴△HAD≌△EDC(SAS),
∴∠ADH=∠DCE,
∵∠ADH+∠HDC=∠DCE+∠HDC=90°,
∴∠DFC=90°,
∴CE⊥DH;
(2)如图2,过F作FG⊥AD,交DA的延长线于G,
∵FH⊥AO,
∴∠G=∠GAH=∠AHF=90°,
∴四边形AGFH是矩形,
∴FG=AH=DE,∠G=90°,
在△GFE和△DEC中,
,
∴△GFE≌△DEC(AAS),
∴EG=DC=AD,
∴EG﹣AE=AD﹣AE,
∴AG=DE=FH=AH,
∴FH=AH.
同课章节目录
