3.1.1.3函数的表示方法(习题)-2021-2022学年高一上学期数学人教B版(2019)必修第一册(Word含答案解析)
文档属性
| 名称 | 3.1.1.3函数的表示方法(习题)-2021-2022学年高一上学期数学人教B版(2019)必修第一册(Word含答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 333.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 00:00:00 | ||
图片预览


文档简介
函数的表示方法
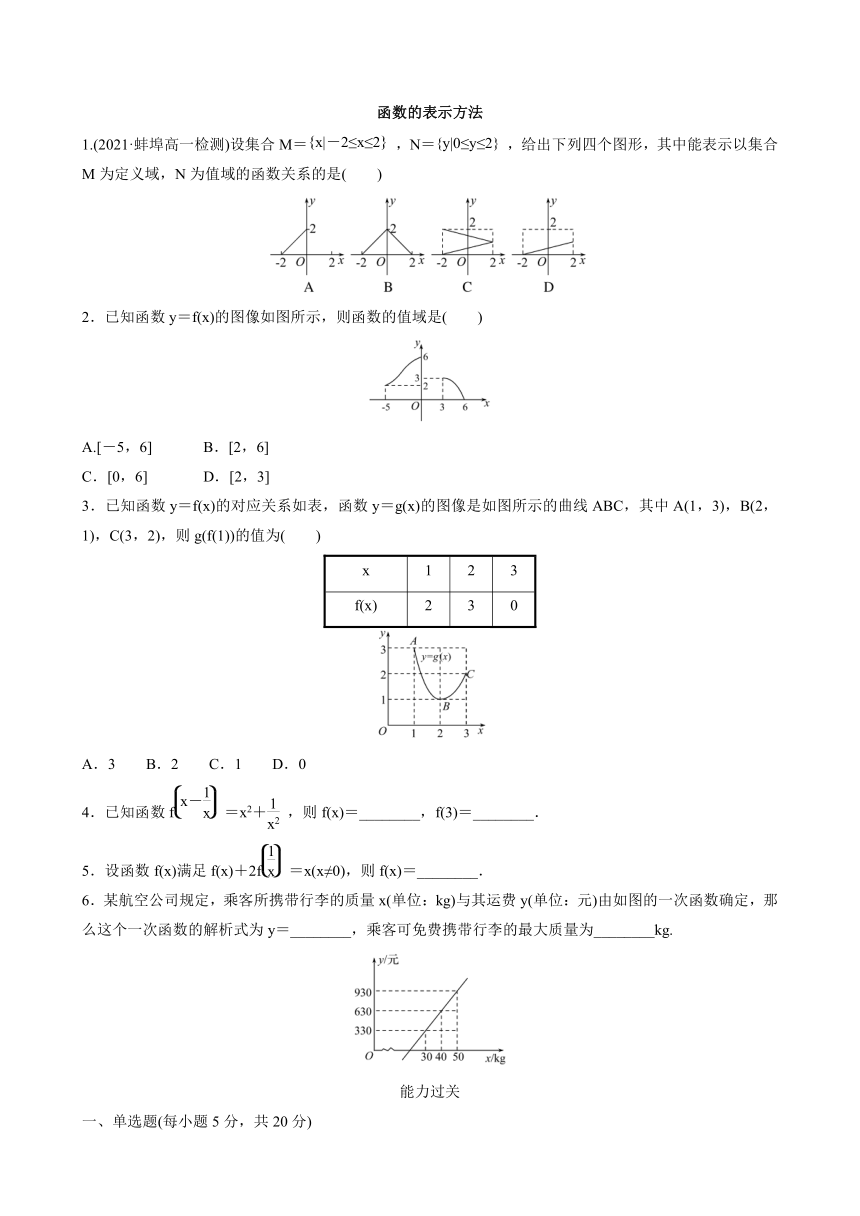
1.(2021·蚌埠高一检测)设集合M=,N=,给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是( )
2.已知函数y=f(x)的图像如图所示,则函数的值域是( )
A.[-5,6] B.[2,6]
C.[0,6] D.[2,3]
3.已知函数y=f(x)的对应关系如表,函数y=g(x)的图像是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则g(f(1))的值为( )
x 1 2 3
f(x) 2 3 0
A.3 B.2 C.1 D.0
4.已知函数f=x2+,则f(x)=________,f(3)=________.
5.设函数f(x)满足f(x)+2f=x(x≠0),则f(x)=________.
6.某航空公司规定,乘客所携带行李的质量x(单位:kg)与其运费y(单位:元)由如图的一次函数确定,那么这个一次函数的解析式为y=________,乘客可免费携带行李的最大质量为________kg.
能力过关
一、单选题(每小题5分,共20分)
1.(2021·烟台高一检测)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,下列图像中与上述事件吻合最好的是( )
2.等腰三角形的周长为20,底边长y是一腰长x的函数,则( )
A.y=10-x(0<x≤10)
B.y=10-x(0<x<10)
C.y=20-2x(5≤x≤10)
D.y=20-2x(5<x<10)
3.函数y=ax2+bx+c与y=ax+b(ab≠0)的图像只可能是( )
4.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )
A.(0,4] B.
C. D.
二、多选题(每小题5分,共10分,全部选对的得5分,选对但不全的得3分,有选错的得0分)
5.(2021·辽阳高一检测)已知函数f(x)是一次函数,满足f=9x+8,则f(x)的解析式可能为( )
A.f(x)=3x+2 B.f(x)=3x-2
C.f(x)=-3x+4 D.f(x)=-3x-4
6.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙与甲跑的路程一样多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
三、填空题(每小题5分,共10分)
7.函数f(x)=x+1,x∈{-1,1,2}的值域是________;函数g(x)=3x-的值域为________.
8.若一个长方体的高为80 cm,长比宽多10 cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.
四、解答题(每小题10分,共20分)
9.已知函数f(+2)=3x++2,求函数f(x)的解析式,并写出其定义域.
10.已知二次函数f(x)满足f(0)=f(4),且f(x)=0的两根平方和为10,图像过(0,3)点,求f(x)的解析式.
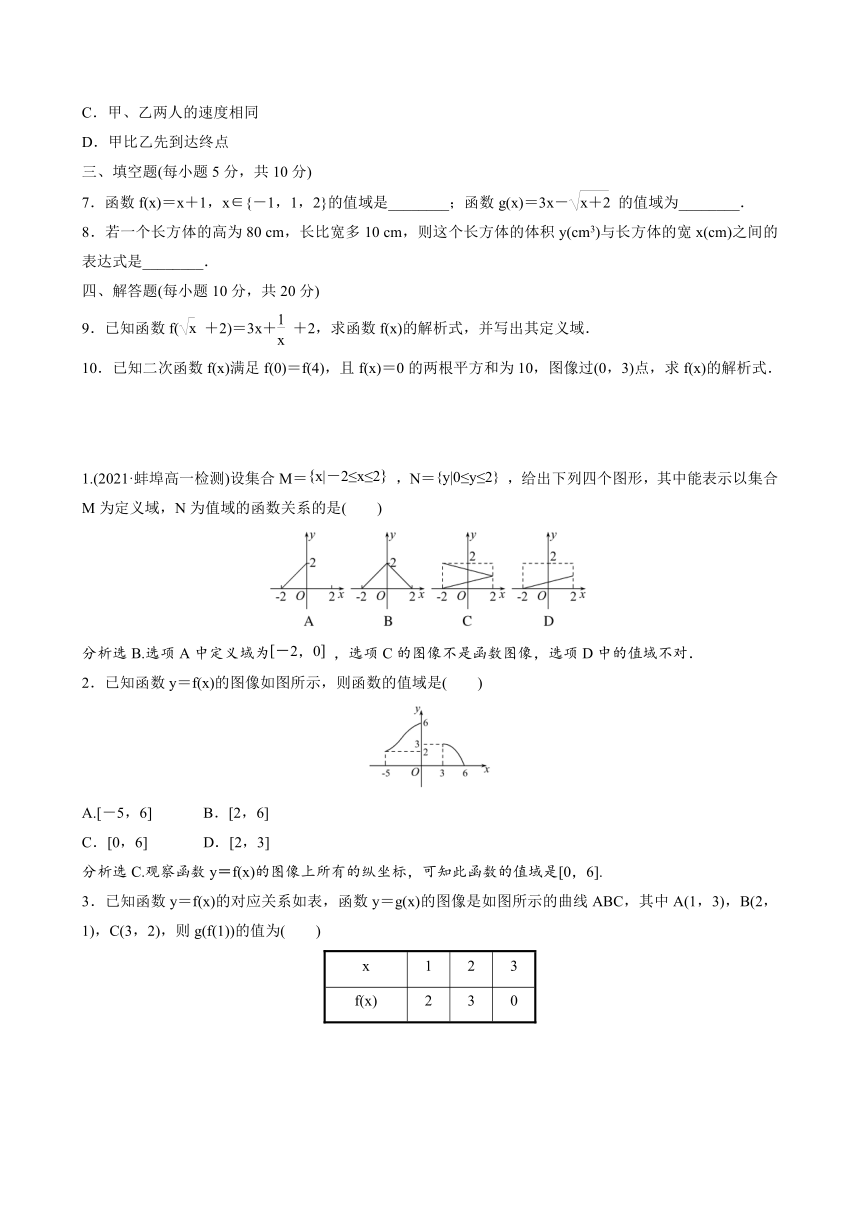
1.(2021·蚌埠高一检测)设集合M=,N=,给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是( )
分析选B.选项A中定义域为,选项C的图像不是函数图像,选项D中的值域不对.
2.已知函数y=f(x)的图像如图所示,则函数的值域是( )
A.[-5,6] B.[2,6]
C.[0,6] D.[2,3]
分析选C.观察函数y=f(x)的图像上所有的纵坐标,可知此函数的值域是[0,6].
3.已知函数y=f(x)的对应关系如表,函数y=g(x)的图像是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则g(f(1))的值为( )
x 1 2 3
f(x) 2 3 0
A.3 B.2 C.1 D.0
分析选C.由y=g(x)的图像及y=f(x)的对应关系表得g(f(1))= g(2)=1.
4.已知函数f=x2+,则f(x)=________,f(3)=________.
分析因为f=x2+=+2,所以f(x)=x2+2,所以f(3)=32+2=11.
答案:x2+2 11
5.设函数f(x)满足f(x)+2f=x(x≠0),则f(x)=________.
分析因为对任意x∈R且x≠0都有f(x)+
2f=x成立.所以对于∈R,有f+2f(x)=,两式组成方程组
②×2-①整理得:f(x)=.
答案:
6.某航空公司规定,乘客所携带行李的质量x(单位:kg)与其运费y(单位:元)由如图的一次函数确定,那么这个一次函数的解析式为y=________,乘客可免费携带行李的最大质量为________kg.
分析设一次函数解析式为y=ax+b(a≠0),
代入点(30,330)与点(40,630),得
解得即y=30x-570,
若要免费,则y≤0,所以x≤19.
答案:30x-570 19
能力过关
一、单选题(每小题5分,共20分)
1.(2021·烟台高一检测)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,下列图像中与上述事件吻合最好的是( )
分析选C.由题意,该高三学生离开家,y是x的一次函数,且斜率为正;
高三学生返回家的过程中,y仍然是x的一次函数,斜率为负;
高三学生最后由家乘坐出租车以更快的速度赶往高铁站,
y仍然是x的一次函数,斜率为正值,且斜率比第一段的斜率大,
则图像先增再减再增,且第三段的斜率大于第一段的斜率,
所以与事件吻合最好的图像为C.
2.等腰三角形的周长为20,底边长y是一腰长x的函数,则( )
A.y=10-x(0<x≤10)
B.y=10-x(0<x<10)
C.y=20-2x(5≤x≤10)
D.y=20-2x(5<x<10)
分析选D.因为2x+y=20,所以y=20-2x,
解不等式组得5<x<10.
3.函数y=ax2+bx+c与y=ax+b(ab≠0)的图像只可能是( )
分析选D.由a的符号排除B,C,又A中y轴为抛物线的对称轴,即b=0,也应排除.
4.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )
A.(0,4] B.
C. D.
分析选C.因为y=x2-3x-4=-,所以对称轴为直线x=,当x=时,y=-.因为x=0时,y=-4,由二次函数图像可知
解得≤m≤3,所以m的取值范围是.
二、多选题(每小题5分,共10分,全部选对的得5分,选对但不全的得3分,有选错的得0分)
5.(2021·辽阳高一检测)已知函数f(x)是一次函数,满足f=9x+8,则f(x)的解析式可能为( )
A.f(x)=3x+2 B.f(x)=3x-2
C.f(x)=-3x+4 D.f(x)=-3x-4
分析选AD.设f(x)=kx+b(k≠0),由题意可知f=k+b=k2x+kb+b=9x+8,
所以,解得或,
所以f(x)=3x+2或f(x)=-3x-4.
6.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙与甲跑的路程一样多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
分析选BD.从图中直线看出s甲=s乙;甲、乙同时出发,跑了相同的路程,甲先于乙到达.
三、填空题(每小题5分,共10分)
7.函数f(x)=x+1,x∈{-1,1,2}的值域是________;函数g(x)=3x-的值域为________.
分析f(x)=x+1,x∈,当x=-1时,f(-1)=-1+1=0;当x=1时,f(1)=1+1=2;当x=2时,f(2)=2+1=3,所以函数f(x)=x+1,x∈的值域为;
令t=(t≥0),则x=t2-2,换元可得函数的解析式h(t)=3-t=3t2-t-6(t≥0),
二次函数h(t)开口向上,对称轴为t=-=>0,结合二次函数的性质可得函数h(t)的最小值为h=-,所以函数h(t)的值域为.
答案:
8.若一个长方体的高为80 cm,长比宽多10 cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.
分析由题意可知,长方体的长为(x+10)cm,从而长方体的体积y=80x(x+10),x>0.
答案:y=80x(x+10),x∈(0,+∞)
四、解答题(每小题10分,共20分)
9.已知函数f(+2)=3x++2,求函数f(x)的解析式,并写出其定义域.
分析令t=+2,t>2,则x=(t-2)2,
所以f(t)=3(t-2)2++2,所以f(x)=3(x-2)2++2,其定义域为(2,+∞).
10.已知二次函数f(x)满足f(0)=f(4),且f(x)=0的两根平方和为10,图像过(0,3)点,求f(x)的解析式.
分析设f(x)=ax2+bx+c(a≠0).
由f(0)=f(4)知得4a+b=0.①
又图像过(0,3)点,所以c=3.②
设f(x)=0的两实根为x1,x2,
则x1+x2=-,x1x2=.
所以x+x=(x1+x2)2-2x1x2=-
2·=10.即b2-2ac=10a2.③由①②③得a=1,b=-4,c=3.所以f(x)=x2-4x+3.
1.(2021·蚌埠高一检测)设集合M=,N=,给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是( )
2.已知函数y=f(x)的图像如图所示,则函数的值域是( )
A.[-5,6] B.[2,6]
C.[0,6] D.[2,3]
3.已知函数y=f(x)的对应关系如表,函数y=g(x)的图像是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则g(f(1))的值为( )
x 1 2 3
f(x) 2 3 0
A.3 B.2 C.1 D.0
4.已知函数f=x2+,则f(x)=________,f(3)=________.
5.设函数f(x)满足f(x)+2f=x(x≠0),则f(x)=________.
6.某航空公司规定,乘客所携带行李的质量x(单位:kg)与其运费y(单位:元)由如图的一次函数确定,那么这个一次函数的解析式为y=________,乘客可免费携带行李的最大质量为________kg.
能力过关
一、单选题(每小题5分,共20分)
1.(2021·烟台高一检测)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,下列图像中与上述事件吻合最好的是( )
2.等腰三角形的周长为20,底边长y是一腰长x的函数,则( )
A.y=10-x(0<x≤10)
B.y=10-x(0<x<10)
C.y=20-2x(5≤x≤10)
D.y=20-2x(5<x<10)
3.函数y=ax2+bx+c与y=ax+b(ab≠0)的图像只可能是( )
4.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )
A.(0,4] B.
C. D.
二、多选题(每小题5分,共10分,全部选对的得5分,选对但不全的得3分,有选错的得0分)
5.(2021·辽阳高一检测)已知函数f(x)是一次函数,满足f=9x+8,则f(x)的解析式可能为( )
A.f(x)=3x+2 B.f(x)=3x-2
C.f(x)=-3x+4 D.f(x)=-3x-4
6.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙与甲跑的路程一样多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
三、填空题(每小题5分,共10分)
7.函数f(x)=x+1,x∈{-1,1,2}的值域是________;函数g(x)=3x-的值域为________.
8.若一个长方体的高为80 cm,长比宽多10 cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.
四、解答题(每小题10分,共20分)
9.已知函数f(+2)=3x++2,求函数f(x)的解析式,并写出其定义域.
10.已知二次函数f(x)满足f(0)=f(4),且f(x)=0的两根平方和为10,图像过(0,3)点,求f(x)的解析式.
1.(2021·蚌埠高一检测)设集合M=,N=,给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是( )
分析选B.选项A中定义域为,选项C的图像不是函数图像,选项D中的值域不对.
2.已知函数y=f(x)的图像如图所示,则函数的值域是( )
A.[-5,6] B.[2,6]
C.[0,6] D.[2,3]
分析选C.观察函数y=f(x)的图像上所有的纵坐标,可知此函数的值域是[0,6].
3.已知函数y=f(x)的对应关系如表,函数y=g(x)的图像是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则g(f(1))的值为( )
x 1 2 3
f(x) 2 3 0
A.3 B.2 C.1 D.0
分析选C.由y=g(x)的图像及y=f(x)的对应关系表得g(f(1))= g(2)=1.
4.已知函数f=x2+,则f(x)=________,f(3)=________.
分析因为f=x2+=+2,所以f(x)=x2+2,所以f(3)=32+2=11.
答案:x2+2 11
5.设函数f(x)满足f(x)+2f=x(x≠0),则f(x)=________.
分析因为对任意x∈R且x≠0都有f(x)+
2f=x成立.所以对于∈R,有f+2f(x)=,两式组成方程组
②×2-①整理得:f(x)=.
答案:
6.某航空公司规定,乘客所携带行李的质量x(单位:kg)与其运费y(单位:元)由如图的一次函数确定,那么这个一次函数的解析式为y=________,乘客可免费携带行李的最大质量为________kg.
分析设一次函数解析式为y=ax+b(a≠0),
代入点(30,330)与点(40,630),得
解得即y=30x-570,
若要免费,则y≤0,所以x≤19.
答案:30x-570 19
能力过关
一、单选题(每小题5分,共20分)
1.(2021·烟台高一检测)某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛(山东省赛区)的比赛活动.早上他乘坐出租车从家里出发,离开家不久,发现身份证忘在家里了,于是回到家取上身份证,然后乘坐出租车以更快的速度赶往高铁站,令x(单位:分钟)表示离开家的时间,y(单位:千米)表示离开家的距离,其中等待红绿灯及在家取身份证的时间忽略不计,下列图像中与上述事件吻合最好的是( )
分析选C.由题意,该高三学生离开家,y是x的一次函数,且斜率为正;
高三学生返回家的过程中,y仍然是x的一次函数,斜率为负;
高三学生最后由家乘坐出租车以更快的速度赶往高铁站,
y仍然是x的一次函数,斜率为正值,且斜率比第一段的斜率大,
则图像先增再减再增,且第三段的斜率大于第一段的斜率,
所以与事件吻合最好的图像为C.
2.等腰三角形的周长为20,底边长y是一腰长x的函数,则( )
A.y=10-x(0<x≤10)
B.y=10-x(0<x<10)
C.y=20-2x(5≤x≤10)
D.y=20-2x(5<x<10)
分析选D.因为2x+y=20,所以y=20-2x,
解不等式组得5<x<10.
3.函数y=ax2+bx+c与y=ax+b(ab≠0)的图像只可能是( )
分析选D.由a的符号排除B,C,又A中y轴为抛物线的对称轴,即b=0,也应排除.
4.若函数y=x2-3x-4的定义域为[0,m],值域为,则m的取值范围是( )
A.(0,4] B.
C. D.
分析选C.因为y=x2-3x-4=-,所以对称轴为直线x=,当x=时,y=-.因为x=0时,y=-4,由二次函数图像可知
解得≤m≤3,所以m的取值范围是.
二、多选题(每小题5分,共10分,全部选对的得5分,选对但不全的得3分,有选错的得0分)
5.(2021·辽阳高一检测)已知函数f(x)是一次函数,满足f=9x+8,则f(x)的解析式可能为( )
A.f(x)=3x+2 B.f(x)=3x-2
C.f(x)=-3x+4 D.f(x)=-3x-4
分析选AD.设f(x)=kx+b(k≠0),由题意可知f=k+b=k2x+kb+b=9x+8,
所以,解得或,
所以f(x)=3x+2或f(x)=-3x-4.
6.甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙与甲跑的路程一样多
C.甲、乙两人的速度相同
D.甲比乙先到达终点
分析选BD.从图中直线看出s甲=s乙;甲、乙同时出发,跑了相同的路程,甲先于乙到达.
三、填空题(每小题5分,共10分)
7.函数f(x)=x+1,x∈{-1,1,2}的值域是________;函数g(x)=3x-的值域为________.
分析f(x)=x+1,x∈,当x=-1时,f(-1)=-1+1=0;当x=1时,f(1)=1+1=2;当x=2时,f(2)=2+1=3,所以函数f(x)=x+1,x∈的值域为;
令t=(t≥0),则x=t2-2,换元可得函数的解析式h(t)=3-t=3t2-t-6(t≥0),
二次函数h(t)开口向上,对称轴为t=-=>0,结合二次函数的性质可得函数h(t)的最小值为h=-,所以函数h(t)的值域为.
答案:
8.若一个长方体的高为80 cm,长比宽多10 cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.
分析由题意可知,长方体的长为(x+10)cm,从而长方体的体积y=80x(x+10),x>0.
答案:y=80x(x+10),x∈(0,+∞)
四、解答题(每小题10分,共20分)
9.已知函数f(+2)=3x++2,求函数f(x)的解析式,并写出其定义域.
分析令t=+2,t>2,则x=(t-2)2,
所以f(t)=3(t-2)2++2,所以f(x)=3(x-2)2++2,其定义域为(2,+∞).
10.已知二次函数f(x)满足f(0)=f(4),且f(x)=0的两根平方和为10,图像过(0,3)点,求f(x)的解析式.
分析设f(x)=ax2+bx+c(a≠0).
由f(0)=f(4)知得4a+b=0.①
又图像过(0,3)点,所以c=3.②
设f(x)=0的两实根为x1,x2,
则x1+x2=-,x1x2=.
所以x+x=(x1+x2)2-2x1x2=-
2·=10.即b2-2ac=10a2.③由①②③得a=1,b=-4,c=3.所以f(x)=x2-4x+3.
