黑龙江省鹤岗市一高2020-2021学年高二下学期6月月考数学(文)试题 Word版含答案
文档属性
| 名称 | 黑龙江省鹤岗市一高2020-2021学年高二下学期6月月考数学(文)试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 466.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 09:35:59 | ||
图片预览




文档简介
鹤岗市一高2020-2021学年高二下学期6月月考
文科数学试卷
一、单选题
1.复数false的虚部为 ( )
A.false B.3 C.false D.false
2.设false,则p是q成立的( )条件
A.充分不必要 B.必要不充分 C.充要条件 D.既非充分也非必要
3.若集合false,false,则( )
A.false B.false C.false D.false
4.已知函数false满足false,求false的值为( )
A.false B.false C.false D.false
5.已知函数false,则函数false的定义域为( )
A.false B.false C.false D.false
6.若函数false的值域为false,则false的取值范围是
A.(0,2] B.false C.false D.false
7.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线false平面false,直线false平面false,则直线false直线a”的结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
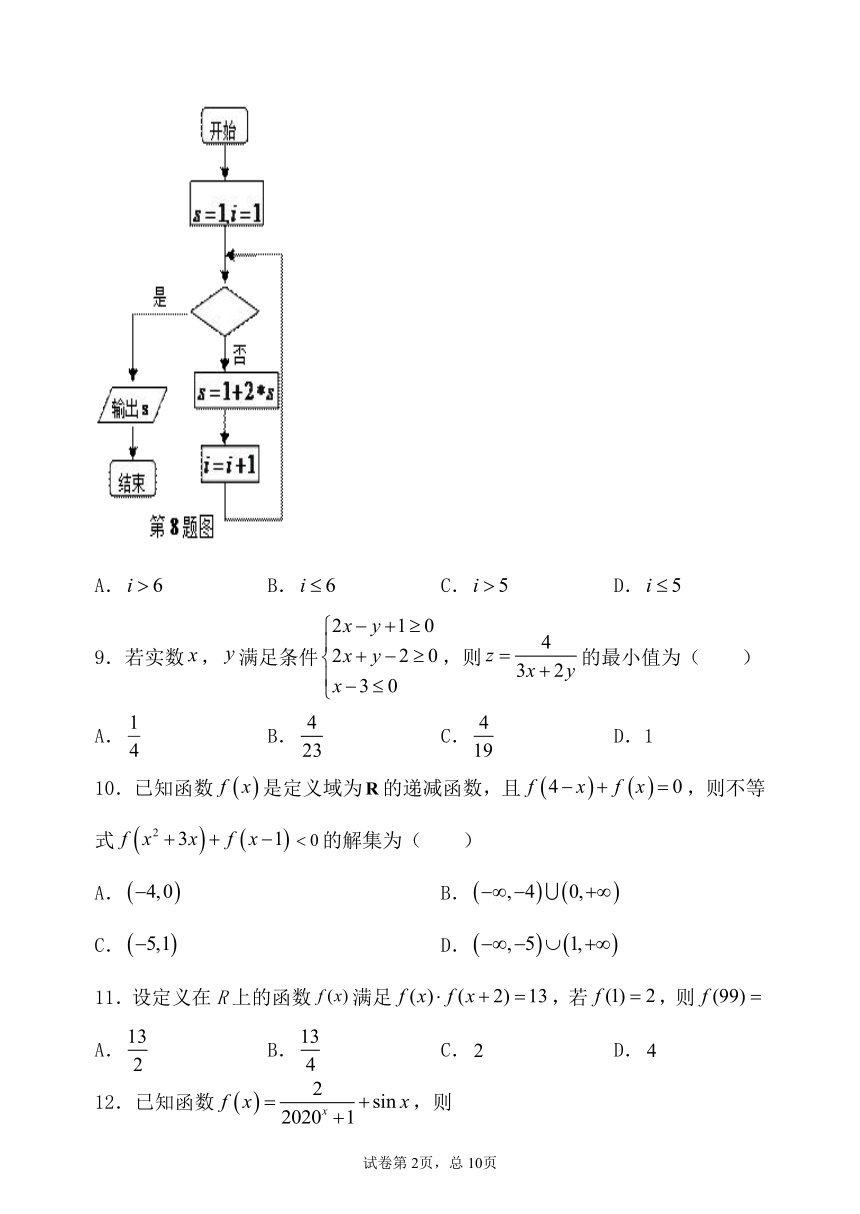
8.下图是把二进制数false化成十进制数的一个程序框图,判断框内应填 入的条件是( )
A.false B.false C.false D.false
9.若实数false,false满足条件false,则false的最小值为( )
A.false B.false C.false D.1
10.已知函数false是定义域为false的递减函数,且false,则不等式falsefalse的解集为( )
A.false B.false
C.false D.false
11.设定义在R上的函数false满足false,若false,则false
A.false B.false C.false D.false
12.已知函数false,则false false( )
A.4040 B.4038 C.2 D.0
二、填空题
13.命题:“false,false”的否定是___________.
14.函数false在false上单调递增,则实数a的取值范围是_________.
15.设函数false是奇函数,且false,则false时,求false____________ .
16.已知函数false,若存在实数false,使得对于任意的实数false都有false成立,则实数false的取值范围是___________.
三、解答题
17.已知时,函数有极值
(1)求实数的值;
(2)若方程有3个实数根,求实数的取值范围。
18.某学生对某小区30位居民的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的,饮食以肉类为主).
(1)根据茎叶图,说明这30位居民中50岁以上的人的饮食习惯;
(2)根据以上数据完成如下2×2列联表;
主食蔬菜
主食肉类
总计
50岁以下
50岁以上
总计
(3)能否有99%的把握认为居民的饮食习惯与年龄有关?
独立性检验的临界值表
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:false,其中false.
19.已知函数false.
(1)若false,求证:false;
(2)若函数false在false上不单调,求实数false的取值范围.
20.某公司对项目A进行生产投资,所获得的利润有如下统计数据表:
项目A投资金额x(百万元)
1
2
3
4
5
所获利润y(百万元)
0.3
0.3
0.5
0.9
1
(1)请用线性回归模型拟合y与x的关系;
(2)该公司计划用7百万元对A,B两个项目进行投资.若公司对项目B投资x(1≤x≤6)百万元所获得的利润y近似满足:false,求A,B两个项目投资金额分别为多少时,获得的总利润最大?
附:对于一组数据false,其回归直线方程false的斜率和截距的最小二乘法估计公式分别为:false,false.
21.已知函数false,false.
false当false时,false,求实数a的取值范围;
false当false时,曲线false和曲线false是否存在公共切线?并说明理由.
22.已知椭圆false(false是参数),A和B是C上的动点,且满足false(O是坐标原点),以O为极点?以x轴的正半轴为极轴建立极坐标系,点D的极坐标为false.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明false为定值,并求false面积的最大值.
参考答案
1.A 2.B 3.B 4.B 5.A 6.D 7.A 8.C 9.B 10.D
11.A 12.B
13.false,false. 14.false 15.f(x)=2x-8 16.false
17.(1)因为,所以f′(x)=3ax2+b.
又因为当x=1时,f(x)的极值为-2,所以,
解得a=1,b=-3.
(2)由(1)可得,f′(x)=3x2-3=3(x+1)(x﹣1),
令f′(x)=0,得x=±1,
当x<﹣1或x>1时f′(x)>0,f(x)单调递增,当﹣1<x<1时,f′(x)<0,f(x)单调递减;
所以当x=﹣1时f(x)取得极大值,f(﹣1),当x=1时f(x)取得极小值,f(1),大致图像如图:
要使方程f(x)=k有3个解,只需k.故实数k的取值范围为(-2,2).
18.(1)由茎叶图可知,30位居民中50岁以上的人饮食多以蔬菜为主;
(2)2×2列联表如下表所示:
主食蔬菜
主食肉类
总计
50岁以下
4
8
12
50岁以上
16
2
18
总计]
20
10
30
(3)由题意,随机变量false的观测值false,
故有99%的把握认为居民的饮食习惯与年龄有关.
19.解:(1)当false时,false,所以false;
当false时,false,false在区间false上单调递减;
当false时,false,false在区间false上单调递增;
所以false是false在区间false上的最小值,所以false.
(2)依题意,false.
若false,则当false时,false,false在区间false上单调递增,不合题意,舍去;
若false,令false,则false.
因为false时,false,所以false在false上单调递增.
因为false,而false,
所以存在false,使得false.
此时函数false在false上单调递减,在false上单调递增,符合条件;
综上所述,实数false的取值范围是false.
20.(1)根据获得的利润有如下统计数据表,
可得false,false,且false
所以false,则false,
所以回归直线方程为:false.
(2)设对B项目投资false(false)百万元,则对A项目投资(false)百万元.
所获总利润falsefalsefalsefalse.
当且仅当false,即false时取等号,
所以对A,B项目分别投资4.5百万元,2.5百万元时,获得总利润最大.
21.解:false令false,则false.
若false,则false,若false,则false.
所以false在false上是增函数,在false上是减函数.
所以false是false的极大值点,也是false的最大值点,即false.
若false恒成立,则只需false,解得false.
所以实数false的取值范围是false.
false假设存在这样的直线false且与曲线false和曲线false分别相切与点false.由false,得false.
曲线false在点false处的切线方程为false,即false.
同理可得,曲线false在点false处的切线方程为false,即false.所以false则false,即false构造函数false false
存在直线false与曲线false和曲线false相切,等价于函数false在false上有零点对于false.当false时,false,false在上单调递增.
当false时,因为false,所以false在false上是减函数.
又false,,所以存在false,使得false,即false.且当false,false时,当false时,false.
综上,false在false上是增函数,在false上是减函数.
所以false是false的极大值,也是最大值,且false.
又false,false,所以false在false内和false内各有一个零点.
故假设成立,即曲线false和曲线false存在公共切线.
22.(1)由题意,椭圆false(false是参数),点D的直角坐标为false,
设点false,false
因为false为false的中点,可得false,
消去参数,可得点false的轨迹方程为false.
(2)由椭圆false(false是参数),可得椭圆C的普通方程为false,
化为极坐标方程是false,变形得false,
因为false,设false,false,所以false(定值),
则false,当false时,false取得最大值为1.
文科数学试卷
一、单选题
1.复数false的虚部为 ( )
A.false B.3 C.false D.false
2.设false,则p是q成立的( )条件
A.充分不必要 B.必要不充分 C.充要条件 D.既非充分也非必要
3.若集合false,false,则( )
A.false B.false C.false D.false
4.已知函数false满足false,求false的值为( )
A.false B.false C.false D.false
5.已知函数false,则函数false的定义域为( )
A.false B.false C.false D.false
6.若函数false的值域为false,则false的取值范围是
A.(0,2] B.false C.false D.false
7.有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线false平面false,直线false平面false,则直线false直线a”的结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
8.下图是把二进制数false化成十进制数的一个程序框图,判断框内应填 入的条件是( )
A.false B.false C.false D.false
9.若实数false,false满足条件false,则false的最小值为( )
A.false B.false C.false D.1
10.已知函数false是定义域为false的递减函数,且false,则不等式falsefalse的解集为( )
A.false B.false
C.false D.false
11.设定义在R上的函数false满足false,若false,则false
A.false B.false C.false D.false
12.已知函数false,则false false( )
A.4040 B.4038 C.2 D.0
二、填空题
13.命题:“false,false”的否定是___________.
14.函数false在false上单调递增,则实数a的取值范围是_________.
15.设函数false是奇函数,且false,则false时,求false____________ .
16.已知函数false,若存在实数false,使得对于任意的实数false都有false成立,则实数false的取值范围是___________.
三、解答题
17.已知时,函数有极值
(1)求实数的值;
(2)若方程有3个实数根,求实数的取值范围。
18.某学生对某小区30位居民的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的,饮食以肉类为主).
(1)根据茎叶图,说明这30位居民中50岁以上的人的饮食习惯;
(2)根据以上数据完成如下2×2列联表;
主食蔬菜
主食肉类
总计
50岁以下
50岁以上
总计
(3)能否有99%的把握认为居民的饮食习惯与年龄有关?
独立性检验的临界值表
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:false,其中false.
19.已知函数false.
(1)若false,求证:false;
(2)若函数false在false上不单调,求实数false的取值范围.
20.某公司对项目A进行生产投资,所获得的利润有如下统计数据表:
项目A投资金额x(百万元)
1
2
3
4
5
所获利润y(百万元)
0.3
0.3
0.5
0.9
1
(1)请用线性回归模型拟合y与x的关系;
(2)该公司计划用7百万元对A,B两个项目进行投资.若公司对项目B投资x(1≤x≤6)百万元所获得的利润y近似满足:false,求A,B两个项目投资金额分别为多少时,获得的总利润最大?
附:对于一组数据false,其回归直线方程false的斜率和截距的最小二乘法估计公式分别为:false,false.
21.已知函数false,false.
false当false时,false,求实数a的取值范围;
false当false时,曲线false和曲线false是否存在公共切线?并说明理由.
22.已知椭圆false(false是参数),A和B是C上的动点,且满足false(O是坐标原点),以O为极点?以x轴的正半轴为极轴建立极坐标系,点D的极坐标为false.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明false为定值,并求false面积的最大值.
参考答案
1.A 2.B 3.B 4.B 5.A 6.D 7.A 8.C 9.B 10.D
11.A 12.B
13.false,false. 14.false 15.f(x)=2x-8 16.false
17.(1)因为,所以f′(x)=3ax2+b.
又因为当x=1时,f(x)的极值为-2,所以,
解得a=1,b=-3.
(2)由(1)可得,f′(x)=3x2-3=3(x+1)(x﹣1),
令f′(x)=0,得x=±1,
当x<﹣1或x>1时f′(x)>0,f(x)单调递增,当﹣1<x<1时,f′(x)<0,f(x)单调递减;
所以当x=﹣1时f(x)取得极大值,f(﹣1),当x=1时f(x)取得极小值,f(1),大致图像如图:
要使方程f(x)=k有3个解,只需k.故实数k的取值范围为(-2,2).
18.(1)由茎叶图可知,30位居民中50岁以上的人饮食多以蔬菜为主;
(2)2×2列联表如下表所示:
主食蔬菜
主食肉类
总计
50岁以下
4
8
12
50岁以上
16
2
18
总计]
20
10
30
(3)由题意,随机变量false的观测值false,
故有99%的把握认为居民的饮食习惯与年龄有关.
19.解:(1)当false时,false,所以false;
当false时,false,false在区间false上单调递减;
当false时,false,false在区间false上单调递增;
所以false是false在区间false上的最小值,所以false.
(2)依题意,false.
若false,则当false时,false,false在区间false上单调递增,不合题意,舍去;
若false,令false,则false.
因为false时,false,所以false在false上单调递增.
因为false,而false,
所以存在false,使得false.
此时函数false在false上单调递减,在false上单调递增,符合条件;
综上所述,实数false的取值范围是false.
20.(1)根据获得的利润有如下统计数据表,
可得false,false,且false
所以false,则false,
所以回归直线方程为:false.
(2)设对B项目投资false(false)百万元,则对A项目投资(false)百万元.
所获总利润falsefalsefalsefalse.
当且仅当false,即false时取等号,
所以对A,B项目分别投资4.5百万元,2.5百万元时,获得总利润最大.
21.解:false令false,则false.
若false,则false,若false,则false.
所以false在false上是增函数,在false上是减函数.
所以false是false的极大值点,也是false的最大值点,即false.
若false恒成立,则只需false,解得false.
所以实数false的取值范围是false.
false假设存在这样的直线false且与曲线false和曲线false分别相切与点false.由false,得false.
曲线false在点false处的切线方程为false,即false.
同理可得,曲线false在点false处的切线方程为false,即false.所以false则false,即false构造函数false false
存在直线false与曲线false和曲线false相切,等价于函数false在false上有零点对于false.当false时,false,false在上单调递增.
当false时,因为false,所以false在false上是减函数.
又false,,所以存在false,使得false,即false.且当false,false时,当false时,false.
综上,false在false上是增函数,在false上是减函数.
所以false是false的极大值,也是最大值,且false.
又false,false,所以false在false内和false内各有一个零点.
故假设成立,即曲线false和曲线false存在公共切线.
22.(1)由题意,椭圆false(false是参数),点D的直角坐标为false,
设点false,false
因为false为false的中点,可得false,
消去参数,可得点false的轨迹方程为false.
(2)由椭圆false(false是参数),可得椭圆C的普通方程为false,
化为极坐标方程是false,变形得false,
因为false,设false,false,所以false(定值),
则false,当false时,false取得最大值为1.
同课章节目录
