17.1-3勾股定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 17.1-3勾股定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 10:59:32 | ||
图片预览

文档简介
授课人
年级 八 学科 数学 授课时间
课题 17.1勾股定理3 课型 新授
学习 目标 1、能利用勾股定理,根据直角三角形的两边长求第三条边;并在数轴上表示无理数。
2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。
学习 关键 重点 利用勾股定理在数轴上表示无理数
难点 确定以无理数为斜边的直角三角形的两条直角边长
学教过程 二次备课
一.探究新知 1、探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
分析:(1)若能画出长为的线段,就能在数轴上画出表示的点.
(2)由勾股定理知,直角边为1的等腰Rt△,斜边为.因此在数轴上能表示的点.那么长为的线段能否是直角边为正整数的直角三角形的斜边呢?
2.作法:在数轴上找到点A,使OA=_____,作直线垂直于OA,在上取点B,使AB=____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点。
练习1、在数轴上画出表示的点?(尺规作图)
练习2、如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M的横坐标为( ) A.2 B.-1 C.-1 D.
二、例题精讲
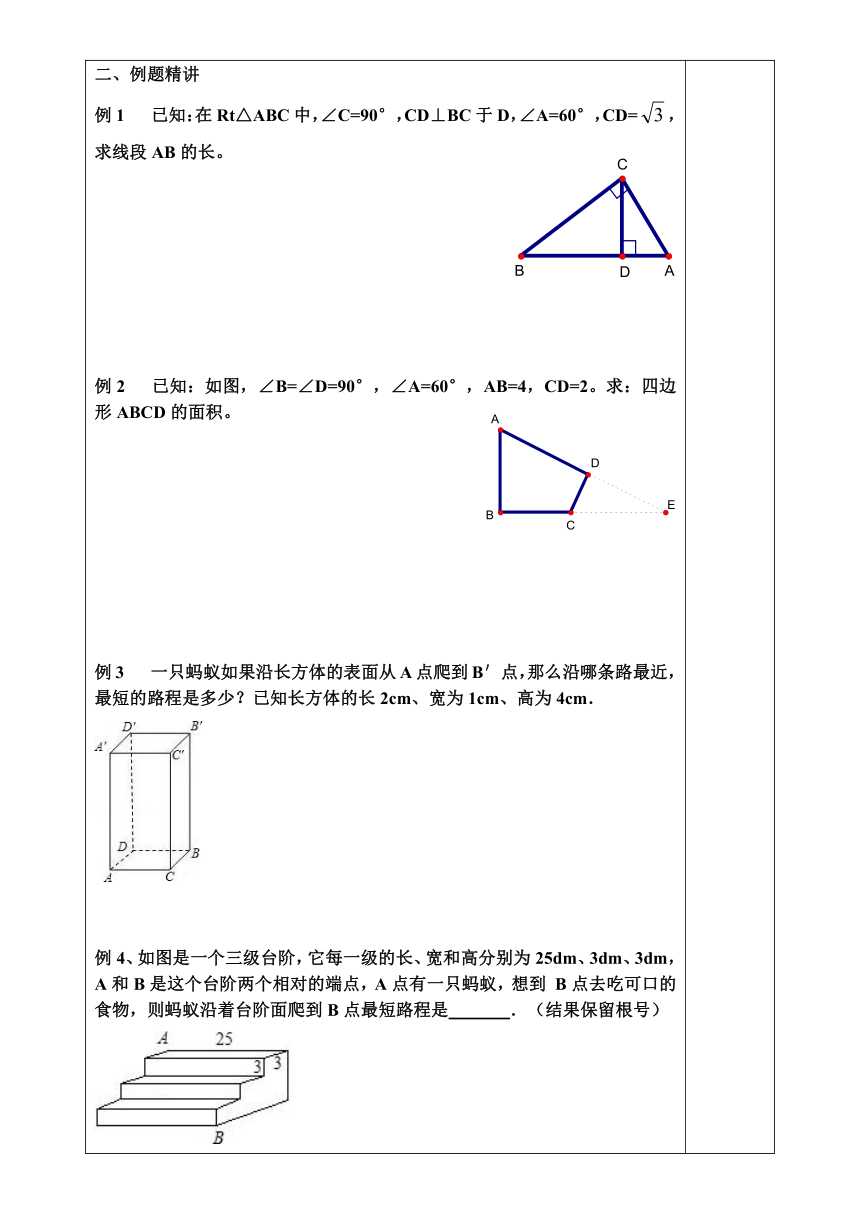
例1 已知:在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=,
求线段AB的长。
例2 已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
例3 一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
例4、如图是一个三级台阶,它每一级的长、宽和高分别为25dm、3dm、3dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到 B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 .(结果保留根号)
四、达标检测 A
(6分)1、如图,等边三角形的边长为6.
求:(1)高AD的长;(2)这个三角形的面积。
B D C
(6分)2、在数轴上画出表示的点
(6分)3、如图,在高为3米,斜坡为5米的一段台阶上铺上地毯,台阶的剖面图如图所示,地毯的长度至少需要多少?
(4分)选做题:等腰直角△ABC中,BC=AC=1,以斜边AB和长度为1的边BB1为直角边构造直角△ABB1,如图,这样构造下去…,则AB3= ;ABn= .
练习2、C
例1 欲求AB,可由AB=BD+CD,分别在两个三角形中利用勾股定理和特殊角,求出BD=3和AD=1。或欲求AB,可由,分别在两个三角形中利用勾股定理和特殊角,求出AC=2和BC=6。
例2 解:延长AD、BC交于E。
∵∠A=∠60°,∠B=90°,∴∠E=30°。
∴AE=2AB=8,CE=2CD=4,
∴BE2=AE2-AB2=82-42=48,BE==。
∵DE2= CE2-CD2=42-22=12,∴DE==。
∴S四边形ABCD=S△ABE-S△CDE=AB·BE-CD·DE=
例3 长方体展开方式有3中,最短路程为5cm
例4
1.欲求高CD,可将其置身于Rt△ADC或Rt△BDC中,
但只有一边已知,根据等腰三角形三线合一性质,可求AD=CD=AB=3cm,则此题可解。
3.7米
选做题.;.
详解:∵等腰直角△ABC中,BC=AC=1,∴AB=,
∵BB1=1,∠ABB1=90°,∴AB1=,
同理可得:AB2=2,AB3=;AB、AB1、AB2、AB3的值可知ABn=.
年级 八 学科 数学 授课时间
课题 17.1勾股定理3 课型 新授
学习 目标 1、能利用勾股定理,根据直角三角形的两边长求第三条边;并在数轴上表示无理数。
2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。
学习 关键 重点 利用勾股定理在数轴上表示无理数
难点 确定以无理数为斜边的直角三角形的两条直角边长
学教过程 二次备课
一.探究新知 1、探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
分析:(1)若能画出长为的线段,就能在数轴上画出表示的点.
(2)由勾股定理知,直角边为1的等腰Rt△,斜边为.因此在数轴上能表示的点.那么长为的线段能否是直角边为正整数的直角三角形的斜边呢?
2.作法:在数轴上找到点A,使OA=_____,作直线垂直于OA,在上取点B,使AB=____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点。
练习1、在数轴上画出表示的点?(尺规作图)
练习2、如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M的横坐标为( ) A.2 B.-1 C.-1 D.
二、例题精讲
例1 已知:在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD=,
求线段AB的长。
例2 已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
例3 一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
例4、如图是一个三级台阶,它每一级的长、宽和高分别为25dm、3dm、3dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到 B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 .(结果保留根号)
四、达标检测 A
(6分)1、如图,等边三角形的边长为6.
求:(1)高AD的长;(2)这个三角形的面积。
B D C
(6分)2、在数轴上画出表示的点
(6分)3、如图,在高为3米,斜坡为5米的一段台阶上铺上地毯,台阶的剖面图如图所示,地毯的长度至少需要多少?
(4分)选做题:等腰直角△ABC中,BC=AC=1,以斜边AB和长度为1的边BB1为直角边构造直角△ABB1,如图,这样构造下去…,则AB3= ;ABn= .
练习2、C
例1 欲求AB,可由AB=BD+CD,分别在两个三角形中利用勾股定理和特殊角,求出BD=3和AD=1。或欲求AB,可由,分别在两个三角形中利用勾股定理和特殊角,求出AC=2和BC=6。
例2 解:延长AD、BC交于E。
∵∠A=∠60°,∠B=90°,∴∠E=30°。
∴AE=2AB=8,CE=2CD=4,
∴BE2=AE2-AB2=82-42=48,BE==。
∵DE2= CE2-CD2=42-22=12,∴DE==。
∴S四边形ABCD=S△ABE-S△CDE=AB·BE-CD·DE=
例3 长方体展开方式有3中,最短路程为5cm
例4
1.欲求高CD,可将其置身于Rt△ADC或Rt△BDC中,
但只有一边已知,根据等腰三角形三线合一性质,可求AD=CD=AB=3cm,则此题可解。
3.7米
选做题.;.
详解:∵等腰直角△ABC中,BC=AC=1,∴AB=,
∵BB1=1,∠ABB1=90°,∴AB1=,
同理可得:AB2=2,AB3=;AB、AB1、AB2、AB3的值可知ABn=.
