17.1-2勾股定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 17.1-2勾股定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 11:02:23 | ||
图片预览


文档简介
授课人
年级 八 学科 数学 授课时间
课题 17.1勾股定理2 课型 新授
学习 目标 1.会用勾股定理进行简单的计算。
2.树立数形结合的思想、分类讨论思想。
学习 关键 重点 勾股定理的简单计算
难点 勾股定理的灵活运用
学教过程 二次备课
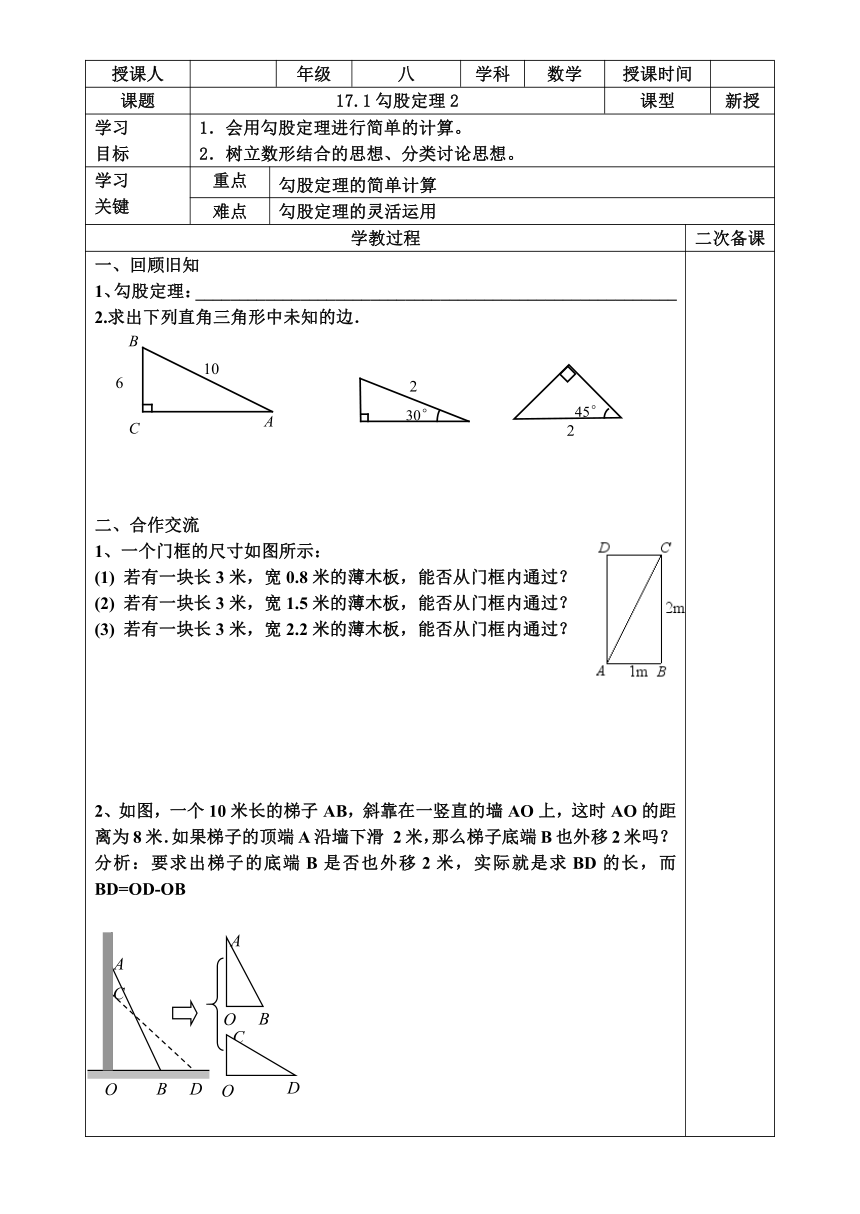
一、回顾旧知 1、勾股定理:_______________________________________________________
2.求出下列直角三角形中未知的边.
二、合作交流
1、一个门框的尺寸如图所示:
(1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?
(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?
(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?
2、如图,一个10米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为8米.如果梯子的顶端A沿墙下滑 2米,那么梯子底端B也外移2米吗?
分析:要求出梯子的底端B是否也外移2米,实际就是求BD的长,而BD=OD-OB
三、例题精讲
例1 如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。
例2 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?
例3 在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
四、达标检测
1.(6分)如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数)
2.(6分)如图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。(精确到1米)
选做题:(10分)
已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=60°,CD=1cm,求BC的长。
一.(1)8 (2)1, (3),
二、OB=6,OD=8,BD=8-6=2,梯子底端B也外移2米。
三.例1、 18米; 例2 、11600;
例3、解:设水池的深度AC为X米,
则芦苇高AD为 (X+1)米.
根据题意得:
BC2+AC2=AB2
∴52+X2 =(X+1)2
25+X2=X2+2X+1
X=12
∴X+1=12+1=13(米)
答:水池的深度为12米,芦苇高为13米.
四.1、57 2、83米,48米,32米; 3.
年级 八 学科 数学 授课时间
课题 17.1勾股定理2 课型 新授
学习 目标 1.会用勾股定理进行简单的计算。
2.树立数形结合的思想、分类讨论思想。
学习 关键 重点 勾股定理的简单计算
难点 勾股定理的灵活运用
学教过程 二次备课
一、回顾旧知 1、勾股定理:_______________________________________________________
2.求出下列直角三角形中未知的边.
二、合作交流
1、一个门框的尺寸如图所示:
(1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?
(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?
(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?
2、如图,一个10米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为8米.如果梯子的顶端A沿墙下滑 2米,那么梯子底端B也外移2米吗?
分析:要求出梯子的底端B是否也外移2米,实际就是求BD的长,而BD=OD-OB
三、例题精讲
例1 如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。
例2 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?
例3 在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
四、达标检测
1.(6分)如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数)
2.(6分)如图,钢索斜拉大桥为等腰三角形,支柱高24米,∠B=∠C=30°,E、F分别为BD、CD中点,试求B、C两点之间的距离,钢索AB和AE的长度。(精确到1米)
选做题:(10分)
已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,AB⊥AC,∠B=60°,CD=1cm,求BC的长。
一.(1)8 (2)1, (3),
二、OB=6,OD=8,BD=8-6=2,梯子底端B也外移2米。
三.例1、 18米; 例2 、11600;
例3、解:设水池的深度AC为X米,
则芦苇高AD为 (X+1)米.
根据题意得:
BC2+AC2=AB2
∴52+X2 =(X+1)2
25+X2=X2+2X+1
X=12
∴X+1=12+1=13(米)
答:水池的深度为12米,芦苇高为13米.
四.1、57 2、83米,48米,32米; 3.
