17.2.2勾股定理的逆定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 17.2.2勾股定理的逆定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 139.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览

文档简介
授课人
年级 八 学科 数学 授课时间
课题 勾股定理的逆定理2 课型 新授
学习 目标 1.灵活应用勾股定理及逆定理解决实际问题。
2.进一步加深性质定理与判定定理之间关系的认识。
学习 关键 重点 灵活应用勾股定理及逆定理解决实际问题
难点 灵活应用勾股定理及逆定理解决实际问题
学教过程 二次备课
一.回顾旧知 1、以下列各组线段为边长,能构成直角三角形的是 。
①3,4,5 ②1,3,4 ③4,4,6 ④6,8,10?
⑤5,7,2? ⑥13,5,12? ⑦7,25,24
2、已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是 度;
3、△ABC的三边长为 9 ,40 ,41 ,则△ABC的面积为 ;
4、若一个三角形的三边之比为5∶12∶13,且周长为60cm,则它的面积为 .
二、 例题精讲
1、 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
2、已知a、b、c为△ABC的三边,满足 ,试判断△ABC的形状.
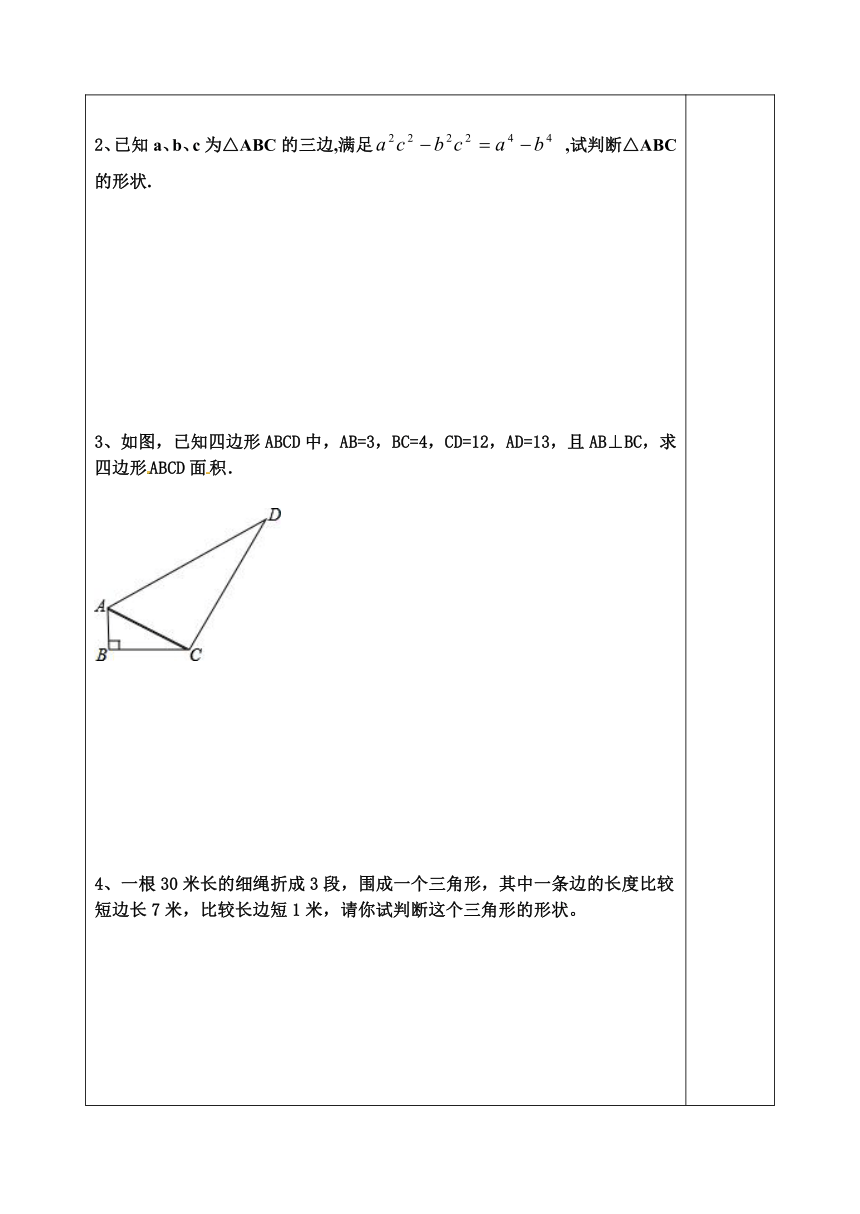
3、如图,已知四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且AB⊥BC,求四边形ABCD面积.
4、一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
三、达标检测
1.(4分)长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个 C 3个 D 4个
(4分)三角形ABC中,∠A.∠B.∠C.的对边分别是a.b.c,且 c+a=2b,
c – a= ,则三角形⊿ABC的形状是 .
3.(4分)小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。
4、(8分)如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
选做题 (8分)
观察第一个数为偶数的勾股数:4、3、5;???6、8、10;???8、15、17;…,若用2n表示第一个偶数,请分别用n的代数式来表示其他两边,并证明确实是勾股数.
一、1.①④⑥⑦ 2.90 3.180 4.120cm2
二、1.依题意可得PR=12×1.5=18,PQ=16×1.5=24,QR=30;
因为242+182=302,PQ2+PR2=QR2,根据勾股定理的逆定理,知∠QPR=90°;
∠PRS=∠QPR-∠QPS=45°。
2.等腰三角形或直角三角形
3.∵AB⊥BC ∴∠B=90°,由勾股数知:AC=5,
∵AC 2+CD 2 =5 2+12 2=169=AD 2,∴△ACD为直角三角形,
∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=36.
4.设未知数列方程,求出三角形的三边长5、12、13;
根据勾股定理的逆定理,由52+122=132,知三角形为直角三角形。
三、1.B 2.直角三角形 3.向正南或正北 4.24 m2
选做题、.2n表示第一个偶数,那么其它两个数为n2-1,n2+1
详解:若用2n表示第一个偶数,那么其它两个数为n2-1,n2+1
∴(2n)2+(n2-1)2=n4+2n2+1=(n2+1)2,∴2n、n2-1、n2+1是一组勾股数.
年级 八 学科 数学 授课时间
课题 勾股定理的逆定理2 课型 新授
学习 目标 1.灵活应用勾股定理及逆定理解决实际问题。
2.进一步加深性质定理与判定定理之间关系的认识。
学习 关键 重点 灵活应用勾股定理及逆定理解决实际问题
难点 灵活应用勾股定理及逆定理解决实际问题
学教过程 二次备课
一.回顾旧知 1、以下列各组线段为边长,能构成直角三角形的是 。
①3,4,5 ②1,3,4 ③4,4,6 ④6,8,10?
⑤5,7,2? ⑥13,5,12? ⑦7,25,24
2、已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是 度;
3、△ABC的三边长为 9 ,40 ,41 ,则△ABC的面积为 ;
4、若一个三角形的三边之比为5∶12∶13,且周长为60cm,则它的面积为 .
二、 例题精讲
1、 “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
2、已知a、b、c为△ABC的三边,满足 ,试判断△ABC的形状.
3、如图,已知四边形ABCD中,AB=3,BC=4,CD=12,AD=13,且AB⊥BC,求四边形ABCD面积.
4、一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
三、达标检测
1.(4分)长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个 C 3个 D 4个
(4分)三角形ABC中,∠A.∠B.∠C.的对边分别是a.b.c,且 c+a=2b,
c – a= ,则三角形⊿ABC的形状是 .
3.(4分)小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。
4、(8分)如图,有一块地,已知,AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
选做题 (8分)
观察第一个数为偶数的勾股数:4、3、5;???6、8、10;???8、15、17;…,若用2n表示第一个偶数,请分别用n的代数式来表示其他两边,并证明确实是勾股数.
一、1.①④⑥⑦ 2.90 3.180 4.120cm2
二、1.依题意可得PR=12×1.5=18,PQ=16×1.5=24,QR=30;
因为242+182=302,PQ2+PR2=QR2,根据勾股定理的逆定理,知∠QPR=90°;
∠PRS=∠QPR-∠QPS=45°。
2.等腰三角形或直角三角形
3.∵AB⊥BC ∴∠B=90°,由勾股数知:AC=5,
∵AC 2+CD 2 =5 2+12 2=169=AD 2,∴△ACD为直角三角形,
∴S四边形ABCD=S△ABC+S△ACD=×3×4+×5×12=36.
4.设未知数列方程,求出三角形的三边长5、12、13;
根据勾股定理的逆定理,由52+122=132,知三角形为直角三角形。
三、1.B 2.直角三角形 3.向正南或正北 4.24 m2
选做题、.2n表示第一个偶数,那么其它两个数为n2-1,n2+1
详解:若用2n表示第一个偶数,那么其它两个数为n2-1,n2+1
∴(2n)2+(n2-1)2=n4+2n2+1=(n2+1)2,∴2n、n2-1、n2+1是一组勾股数.
