17.1-1勾股定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案)
文档属性
| 名称 | 17.1-1勾股定理-2020-2021学年人教版八年级数学下册导学案(表格式 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 64.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 11:38:55 | ||
图片预览

文档简介
授课人
年级 八 学科 数学 授课时间
课题 17.1勾股定理1 课型 新授
学习 目标 了解勾股定理的历史,体验勾股定理的探索过程。
会用不同的方法来验证勾股定理,体会数形结合的思想。
能用勾股定理解决一些实际问题。
学习 关键 重点 勾股定理的内容及证明
难点 勾股定理的证明
学教过程 二次备课
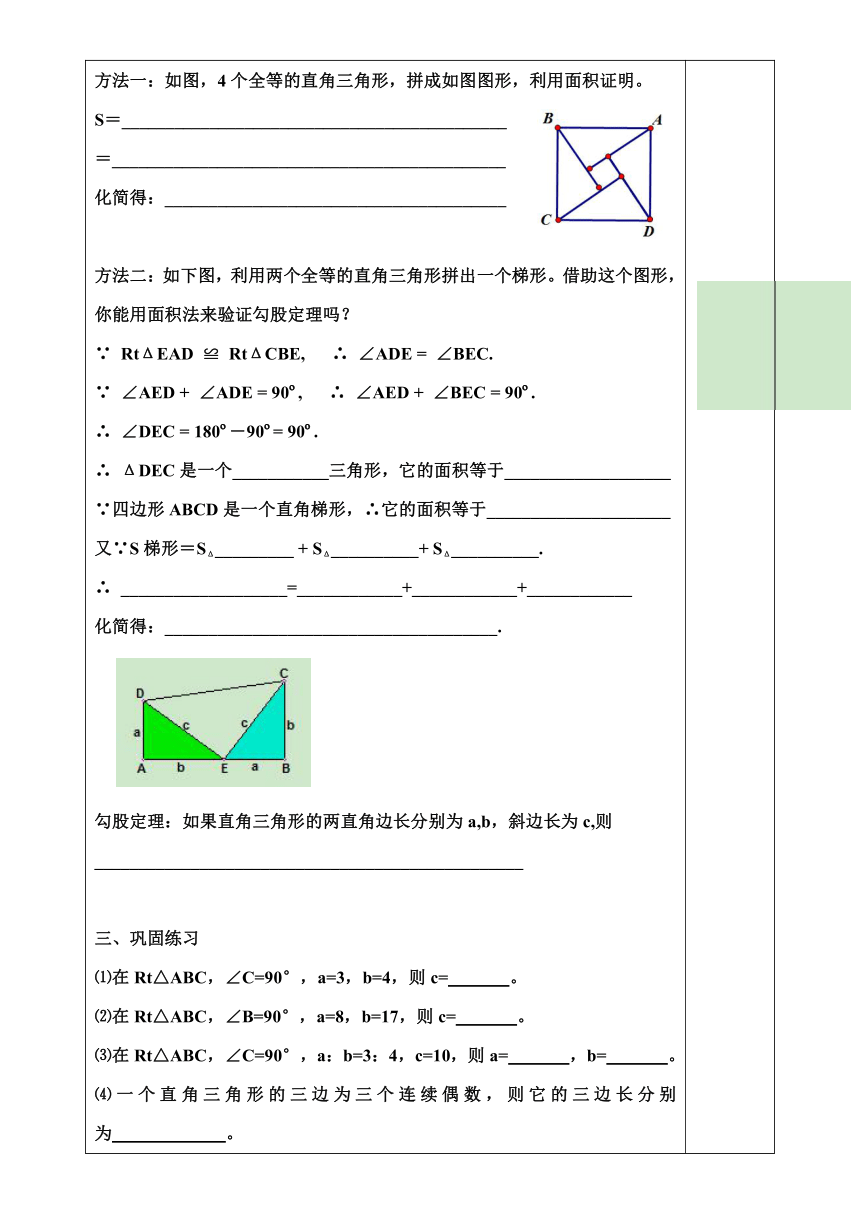
一、自主学习: 1、毕达哥拉斯是古希腊著名的数学家.相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的某种特性。
如图:你能发现图中的等腰直角三角形的性质吗?
请写出你的发现:____________________________________
2、等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点呢?请观察左边的两个图形,完成右边的表格:
提示:以斜边为边长的正方形的面积,等于某个正方形
二、合作交流
猜想:直角三角形的两条直角边的平方和等于斜边的平方.
验证:以直角三角形ABC的两条直角边a,b为边做两个正方形。
方法一:如图,4个全等的直角三角形,拼成如图图形,利用面积证明。
S=____________________________________________
=_____________________________________________
化简得:_______________________________________
方法二:如下图,利用两个全等的直角三角形拼出一个梯形。借助这个图形,你能用面积法来验证勾股定理吗?
∵ RtΔEAD ≌ RtΔCBE, ∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90?, ∴ ∠AED + ∠BEC = 90?.
∴ ∠DEC = 180?―90?= 90?.
∴ ΔDEC是一个___________三角形,它的面积等于___________________
∵四边形ABCD是一个直角梯形,∴它的面积等于_____________________
又∵S梯形=SΔ_________ + SΔ__________+ SΔ__________.
∴ ___________________=____________+____________+____________
化简得:______________________________________.
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,则_________________________________________________
三、巩固练习
⑴在Rt△ABC,∠C=90°,a=3,b=4,则c= 。
⑵在Rt△ABC,∠B=90°,a=8,b=17,则c= 。
⑶在Rt△ABC,∠C=90°,a:b=3:4,c=10,则a= ,b= 。
⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。
四、达标检测
(4分)1、已知直角三角形的两直角边分别为5和12,则斜边长为 ,斜边上的高为 。
(4分)2、已知直角三角形的两边长分别为3cm和5cm,则第三边长为 。
(4分)3、下列各图中所示的线段的长度或正方形的面积为多少。
(注:下列各图中的三角形均为直角三角形)
A= 、 y= 。
(4分)4、在Rt△ABC,∠C=90°,如果c=10,a-b=2,求b。
选做题:(10分)
如下图,4个全等的直角三角形,拼成如图图形,利用面积证明。
分析:左右两边的正方形边长相等,则两个正方形的面积相等。
左边S=__________________________右边S=___________________________
左边和右边面积相等,即 ___________________________________________
化简得_________________________________________________
三.(1)5 (2)15 (3)6,8 (4)6,8,10
四、1、13, 2、4cm或 cm 3、225,39 4、b=6
年级 八 学科 数学 授课时间
课题 17.1勾股定理1 课型 新授
学习 目标 了解勾股定理的历史,体验勾股定理的探索过程。
会用不同的方法来验证勾股定理,体会数形结合的思想。
能用勾股定理解决一些实际问题。
学习 关键 重点 勾股定理的内容及证明
难点 勾股定理的证明
学教过程 二次备课
一、自主学习: 1、毕达哥拉斯是古希腊著名的数学家.相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的某种特性。
如图:你能发现图中的等腰直角三角形的性质吗?
请写出你的发现:____________________________________
2、等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点呢?请观察左边的两个图形,完成右边的表格:
提示:以斜边为边长的正方形的面积,等于某个正方形
二、合作交流
猜想:直角三角形的两条直角边的平方和等于斜边的平方.
验证:以直角三角形ABC的两条直角边a,b为边做两个正方形。
方法一:如图,4个全等的直角三角形,拼成如图图形,利用面积证明。
S=____________________________________________
=_____________________________________________
化简得:_______________________________________
方法二:如下图,利用两个全等的直角三角形拼出一个梯形。借助这个图形,你能用面积法来验证勾股定理吗?
∵ RtΔEAD ≌ RtΔCBE, ∴ ∠ADE = ∠BEC.
∵ ∠AED + ∠ADE = 90?, ∴ ∠AED + ∠BEC = 90?.
∴ ∠DEC = 180?―90?= 90?.
∴ ΔDEC是一个___________三角形,它的面积等于___________________
∵四边形ABCD是一个直角梯形,∴它的面积等于_____________________
又∵S梯形=SΔ_________ + SΔ__________+ SΔ__________.
∴ ___________________=____________+____________+____________
化简得:______________________________________.
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,则_________________________________________________
三、巩固练习
⑴在Rt△ABC,∠C=90°,a=3,b=4,则c= 。
⑵在Rt△ABC,∠B=90°,a=8,b=17,则c= 。
⑶在Rt△ABC,∠C=90°,a:b=3:4,c=10,则a= ,b= 。
⑷一个直角三角形的三边为三个连续偶数,则它的三边长分别为 。
四、达标检测
(4分)1、已知直角三角形的两直角边分别为5和12,则斜边长为 ,斜边上的高为 。
(4分)2、已知直角三角形的两边长分别为3cm和5cm,则第三边长为 。
(4分)3、下列各图中所示的线段的长度或正方形的面积为多少。
(注:下列各图中的三角形均为直角三角形)
A= 、 y= 。
(4分)4、在Rt△ABC,∠C=90°,如果c=10,a-b=2,求b。
选做题:(10分)
如下图,4个全等的直角三角形,拼成如图图形,利用面积证明。
分析:左右两边的正方形边长相等,则两个正方形的面积相等。
左边S=__________________________右边S=___________________________
左边和右边面积相等,即 ___________________________________________
化简得_________________________________________________
三.(1)5 (2)15 (3)6,8 (4)6,8,10
四、1、13, 2、4cm或 cm 3、225,39 4、b=6
