苏科版九年级上册数学 第2章 对称图形 2.7弧长与扇形的面积 同步练习(word版含答案)
文档属性
| 名称 | 苏科版九年级上册数学 第2章 对称图形 2.7弧长与扇形的面积 同步练习(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览

文档简介
2.7弧长与扇形的面积
【思维入门】
1.一个扇形的半径为8
cm,弧长为π
cm,则扇形的圆心角为
( )
A.60° B.120°
C.150°
D.180°
2.如图3-11-1,半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则圆中阴影部分的面积为
( )
A.
cm2
B.
cm2
C.1
cm2
D.
cm2
图3-11-1
图3-11-2
图3-11-3
3.如图3-11-2,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10
cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,C
A′旋转所构成的扇形的弧长为______cm.
4.如图3-11-3,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为____.
5.如图3-11-4,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是____.
图3-11-4
【思维拓展】
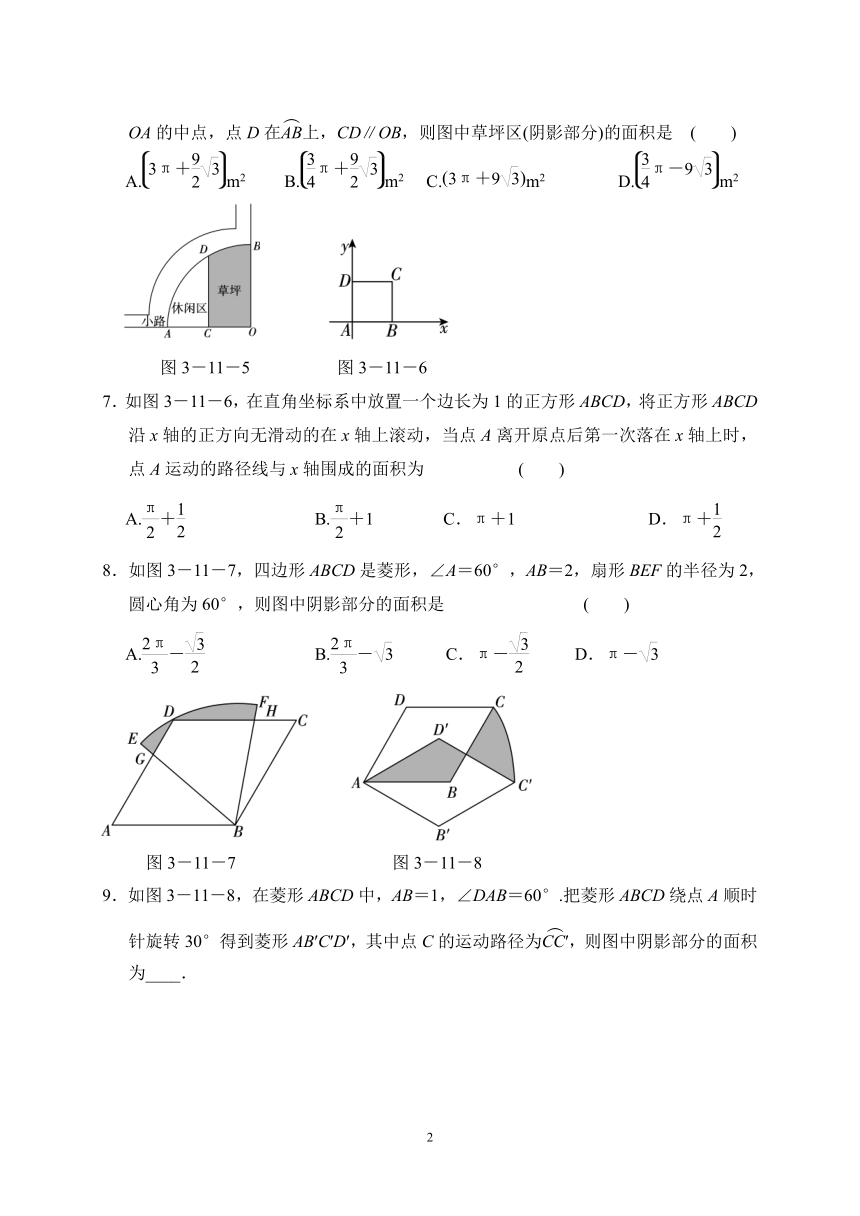
6.如图3-11-5,是某公园的一角,∠AOB=90°,的半径OA长是6
m,点C是OA的中点,点D在上,CD∥OB,则图中草坪区(阴影部分)的面积是
( )
A.m2
B.m2
C.m2
D.m2
图3-11-5
图3-11-6
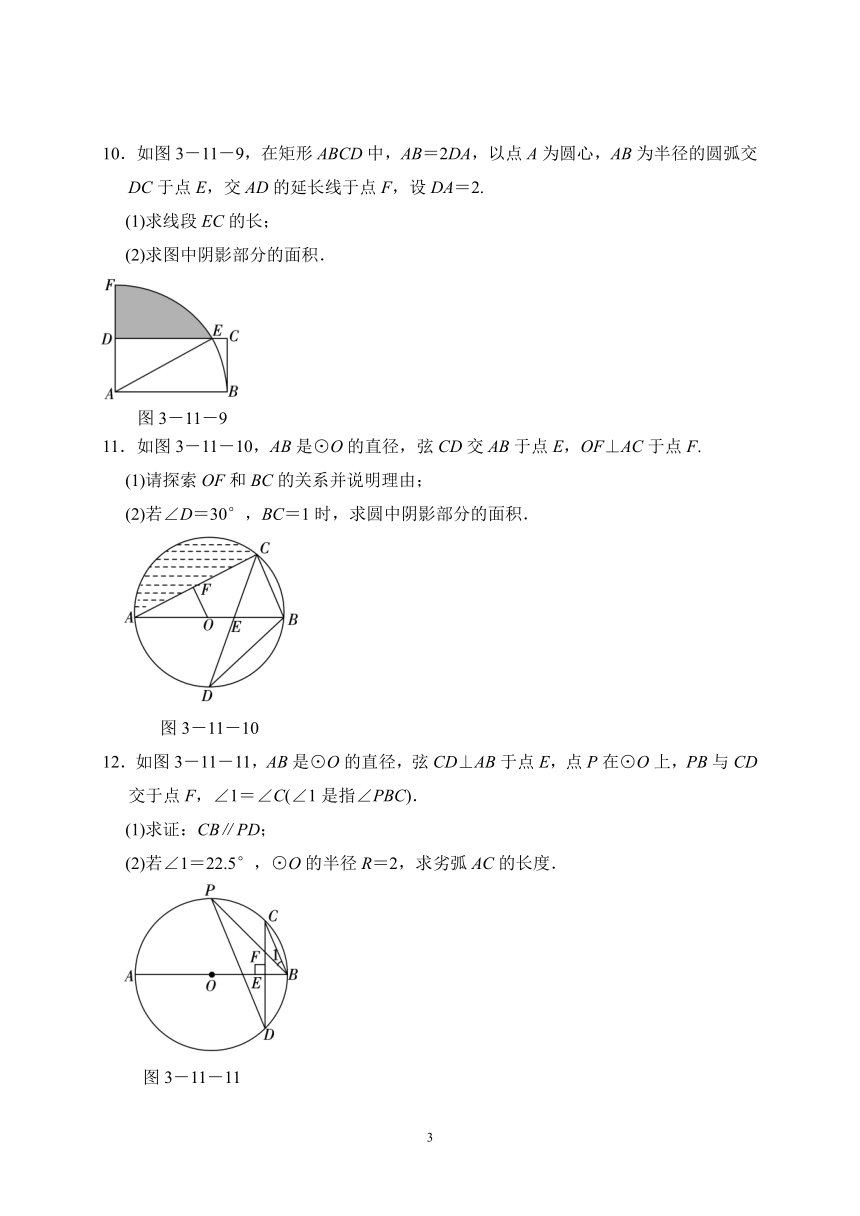
7.如图3-11-6,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
( )
A.+
B.+1
C.π+1
D.π+
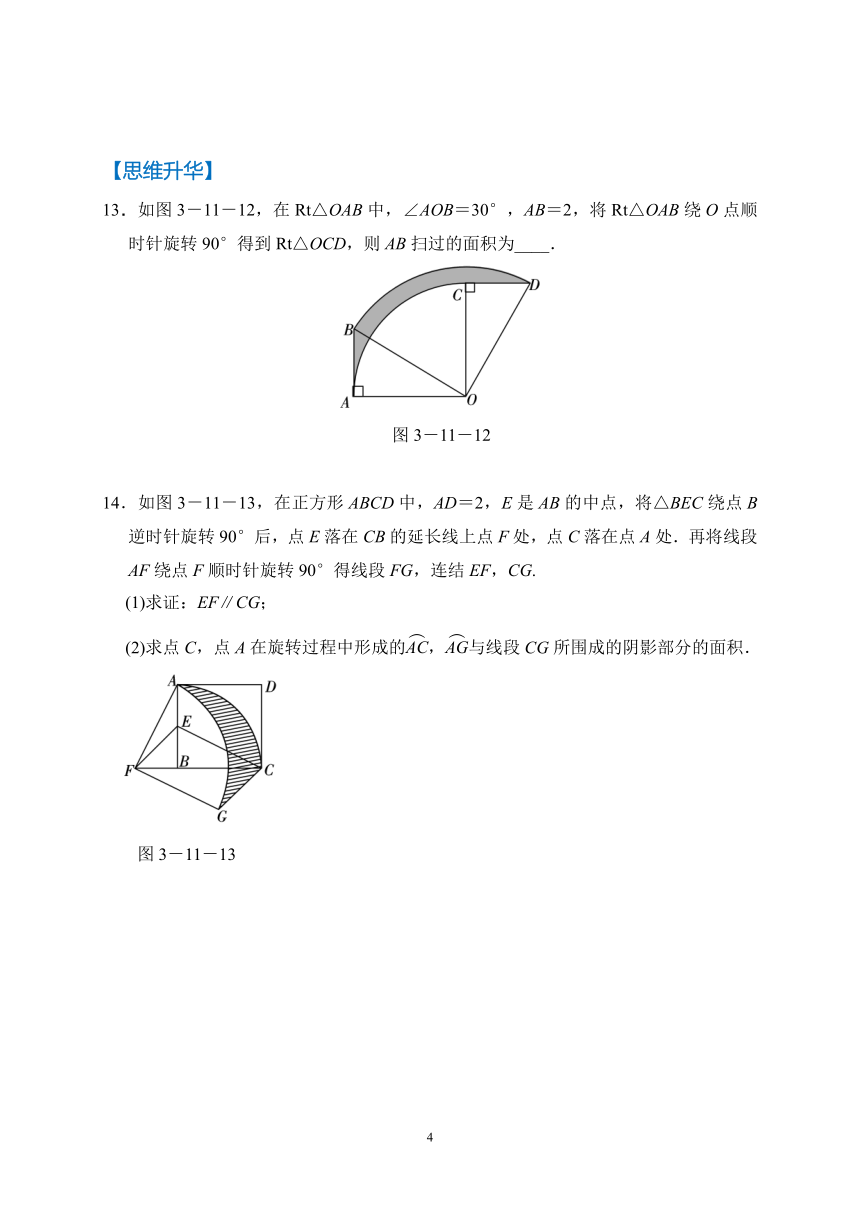
8.如图3-11-7,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是
( )
A.-
B.-
C.π-
D.π-
图3-11-7
图3-11-8
9.如图3-11-8,在菱形ABCD中,AB=1,∠DAB=60°.把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为____.
10.如图3-11-9,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
图3-11-9
11.如图3-11-10,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F.
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.
图3-11-10
12.如图3-11-11,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠1=∠C(∠1是指∠PBC).
(1)求证:CB∥PD;
(2)若∠1=22.5°,⊙O的半径R=2,求劣弧AC的长度.
图3-11-11
【思维升华】
13.如图3-11-12,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为____.
图3-11-12
14.如图3-11-13,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
图3-11-13
答案:
第11讲
弧长与扇形的面积
【思维入门】
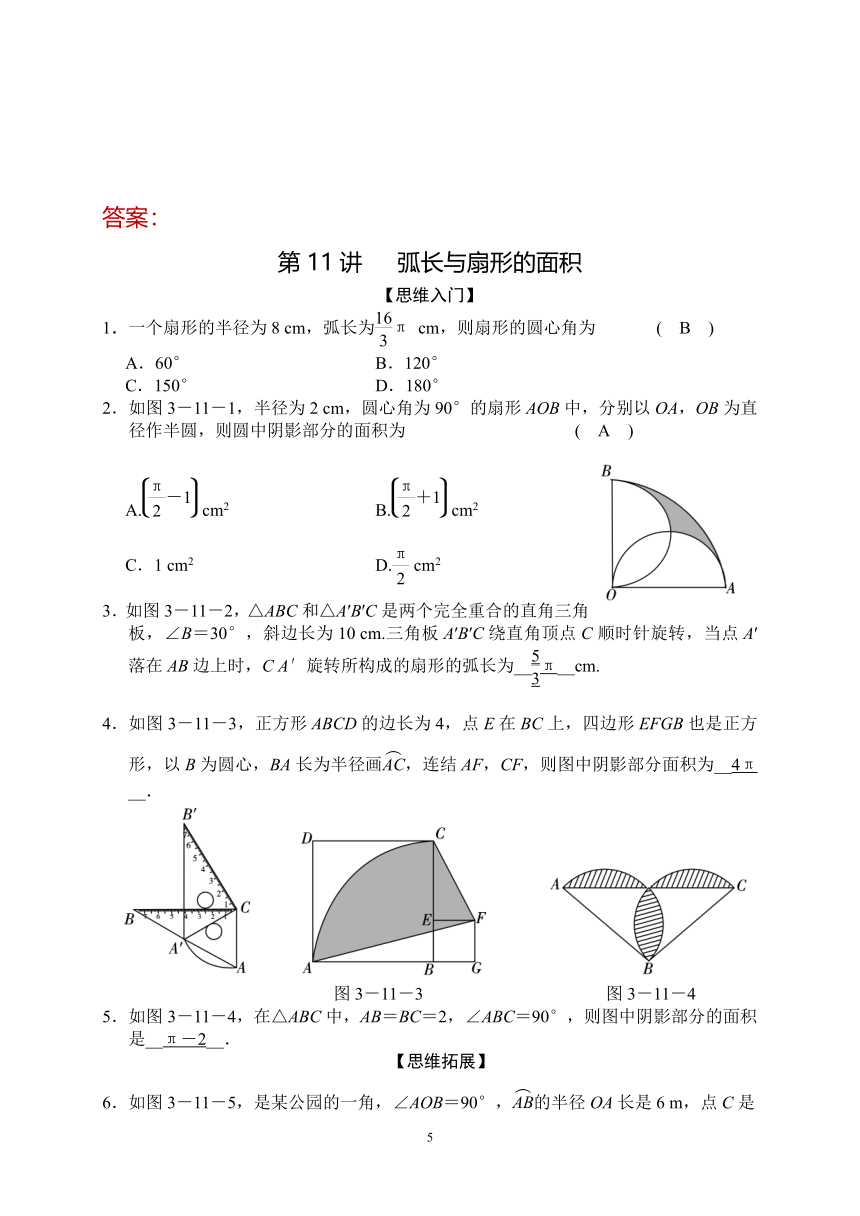
1.一个扇形的半径为8
cm,弧长为π
cm,则扇形的圆心角为
( B )
A.60°
B.120°
C.150°
D.180°
2.如图3-11-1,半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则圆中阴影部分的面积为
( A )
A.
cm2
B.
cm2
C.1
cm2
D.
cm2
3.如图3-11-2,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10
cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,C
A′旋转所构成的扇形的弧长为__π__cm.
如图3-11-3,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为__4π__.
图3-11-3
图3-11-4
5.如图3-11-4,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是__π-2__.
【思维拓展】
6.如图3-11-5,是某公园的一角,∠AOB=90°,的半径OA长是6
m,点C是OA的中点,点D在上,CD∥OB,则图中草坪区(阴影部分)的面积是
( A )
A.m2
B.m2
C.m2
D.m2
7.如图3-11-6,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
( C )
图3-11-6
A.+
B.+1
C.π+1
D.π+
【解析】
如答图所示,
第7题答图
点A运动的路径线与x轴围成的面积=S1+S2+S3+2a=
++
+2×=π+1.
8.如图3-11-7,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是
( B )
图3-11-7
A.-
B.-
C.π-
D.π-
【解析】
如答图,连结BD,∵四边形ABCD是菱形,∠A=60°,
第8题答图
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=2,∴△ABD的高为,
∵扇形BEF的半径为2,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,∴∠3=∠4,
△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是S扇形EBF-S△ABD=-×2×=-.
9.如图3-11-8,在菱形ABCD中,AB=1,∠DAB=60°.把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为__-+__.
图3-11-8
【解析】
如答图,连结CD′和BC′,
∵∠DAB=60°,
∴∠DAC=∠CAB=30°,
∵∠C′AB′=30°,
∴A,D′,C及A,B,C′分别共线,
∴AC=,
∴扇形CAC′的面积为=.
∵AC=AC′,AD′=AB,
∴
∴△OCD′≌△OC′B(AAS).
∴OB=OD′,CO=C′O,
∵∠CBC′=60°,∠BC′O=30°,
∴∠BOC′=90°.
∵CD′=AC-AD′=-1=BC′,
∴在Rt△BOC′中,
BO=-,C′O=-,
∴S△OC′B=·BO·C′O=-,
∴图中阴影部分的面积=S扇形CAC′-2S△OC′B=+-.
10.如图3-11-9,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
解:(1)∵在矩形ABCD中,AB=2DA,
∴AE=2AD,且∠ADE=90°,又∵DA=2,
∴AE=AB=4,
∴DE===2,
∴EC=DC-DE=4-2.
(2)S阴影=S扇形FAE-S△ADE=-×2×2=π-2.
11.如图3-11-10,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F.
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.
图3-11-10
解:(1)OF∥BC,OF=BC.
理由:由垂径定理得AF=CF.
∵AO=BO,
∴OF是△ABC的中位线.
∴OF∥BC,OF=BC.
(2)连结OC,由(1)知OF=.
∵AB是⊙O的直径,∴∠ACB=90°.
∵∠D=30°,∴∠A=30°.
∴AB=2BC=2,∴AC=,
∴S△AOC=×AC×OF=.
∵∠AOC=120°,OA=1,
∴S扇形AOC==.
∴S阴影=S扇形AOC-S△AOC=-.
12.如图3-11-11,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠1=∠C(∠1是指∠PBC).
(1)求证:CB∥PD;
(2)若∠1=22.5°,⊙O的半径R=2,求劣弧AC的长度.
图3-11-11
解:(1)证明:∵P,C,B,D,四点共圆,
第12题答图
∴∠1=∠CDP.
∵∠1=∠C,
∴∠C=∠CDP,
∴CB∥PD.
(2)如答图,连结OC,OD,BD,
∵CD⊥AB,且AB是直径,
∴∠BCD=∠BDC=∠1=22.5°,
∴∠BOC=2∠BDC=45°,
∴∠AOC=135°,
∴弧AC的长度为==π.
【思维升华】
13.如图3-11-12,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为__π__.
图3-11-12
【解析】
∵Rt△OAB中,∠AOB=30°,AB=2,
∴AO=CO=2,BO=DO=4,
∴阴影部分面积=S扇形BOD+S△AOB-S扇形AOC-S△COD=S扇形BOD-S扇形AOC
=-=π.
14.如图3-11-13,在正方形ABCD中,AD=2,E是
AB的中点,将△BEC绕点B逆时针旋转90°后,点E
落在CB的延长线上点F处,点C落在点A处.再将线
段AF绕点F顺时针旋转90°得线段FG,连结EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=AD=2,
∠ABC=90°.
∵△BEC绕点B逆时针旋转90°得△ABF,
∴△ABF≌△CBE,
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,
AF=EC,
∴∠AFB+∠FAB=90°.
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,AF=FG,
∴∠CFG=∠FAB=∠ECB,
∴EC∥FG.
∵AF=EC,AF=FG,
∴EC=FG,
∴四边形EFGC是平行四边形,
∴EF∥CG.
(2)∵△ABF≌△CBE,
∴FB=BE=AB=1,
∴AF==.
在△FEC和△CGF中,
∵EC=FG,∠ECF=∠GFC,FC=CF,
∴△FEC≌△CGF,
∴S△FEC=S△CGF,
∴S阴影=S扇形ABC+S△ABF+S△FGC-S扇形AFG
=+×2×1+×(1+2)×1-
=-.
第9题答图
图3-11-9
图3-11-13
【思维入门】
1.一个扇形的半径为8
cm,弧长为π
cm,则扇形的圆心角为
( )
A.60° B.120°
C.150°
D.180°
2.如图3-11-1,半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则圆中阴影部分的面积为
( )
A.
cm2
B.
cm2
C.1
cm2
D.
cm2
图3-11-1
图3-11-2
图3-11-3
3.如图3-11-2,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10
cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,C
A′旋转所构成的扇形的弧长为______cm.
4.如图3-11-3,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为____.
5.如图3-11-4,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是____.
图3-11-4
【思维拓展】
6.如图3-11-5,是某公园的一角,∠AOB=90°,的半径OA长是6
m,点C是OA的中点,点D在上,CD∥OB,则图中草坪区(阴影部分)的面积是
( )
A.m2
B.m2
C.m2
D.m2
图3-11-5
图3-11-6
7.如图3-11-6,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
( )
A.+
B.+1
C.π+1
D.π+
8.如图3-11-7,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是
( )
A.-
B.-
C.π-
D.π-
图3-11-7
图3-11-8
9.如图3-11-8,在菱形ABCD中,AB=1,∠DAB=60°.把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为____.
10.如图3-11-9,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
图3-11-9
11.如图3-11-10,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F.
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.
图3-11-10
12.如图3-11-11,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠1=∠C(∠1是指∠PBC).
(1)求证:CB∥PD;
(2)若∠1=22.5°,⊙O的半径R=2,求劣弧AC的长度.
图3-11-11
【思维升华】
13.如图3-11-12,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为____.
图3-11-12
14.如图3-11-13,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
图3-11-13
答案:
第11讲
弧长与扇形的面积
【思维入门】
1.一个扇形的半径为8
cm,弧长为π
cm,则扇形的圆心角为
( B )
A.60°
B.120°
C.150°
D.180°
2.如图3-11-1,半径为2
cm,圆心角为90°的扇形AOB中,分别以OA,OB为直径作半圆,则圆中阴影部分的面积为
( A )
A.
cm2
B.
cm2
C.1
cm2
D.
cm2
3.如图3-11-2,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10
cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,C
A′旋转所构成的扇形的弧长为__π__cm.
如图3-11-3,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画,连结AF,CF,则图中阴影部分面积为__4π__.
图3-11-3
图3-11-4
5.如图3-11-4,在△ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是__π-2__.
【思维拓展】
6.如图3-11-5,是某公园的一角,∠AOB=90°,的半径OA长是6
m,点C是OA的中点,点D在上,CD∥OB,则图中草坪区(阴影部分)的面积是
( A )
A.m2
B.m2
C.m2
D.m2
7.如图3-11-6,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
( C )
图3-11-6
A.+
B.+1
C.π+1
D.π+
【解析】
如答图所示,
第7题答图
点A运动的路径线与x轴围成的面积=S1+S2+S3+2a=
++
+2×=π+1.
8.如图3-11-7,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是
( B )
图3-11-7
A.-
B.-
C.π-
D.π-
【解析】
如答图,连结BD,∵四边形ABCD是菱形,∠A=60°,
第8题答图
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=2,∴△ABD的高为,
∵扇形BEF的半径为2,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,∴∠3=∠4,
△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是S扇形EBF-S△ABD=-×2×=-.
9.如图3-11-8,在菱形ABCD中,AB=1,∠DAB=60°.把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为__-+__.
图3-11-8
【解析】
如答图,连结CD′和BC′,
∵∠DAB=60°,
∴∠DAC=∠CAB=30°,
∵∠C′AB′=30°,
∴A,D′,C及A,B,C′分别共线,
∴AC=,
∴扇形CAC′的面积为=.
∵AC=AC′,AD′=AB,
∴
∴△OCD′≌△OC′B(AAS).
∴OB=OD′,CO=C′O,
∵∠CBC′=60°,∠BC′O=30°,
∴∠BOC′=90°.
∵CD′=AC-AD′=-1=BC′,
∴在Rt△BOC′中,
BO=-,C′O=-,
∴S△OC′B=·BO·C′O=-,
∴图中阴影部分的面积=S扇形CAC′-2S△OC′B=+-.
10.如图3-11-9,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
解:(1)∵在矩形ABCD中,AB=2DA,
∴AE=2AD,且∠ADE=90°,又∵DA=2,
∴AE=AB=4,
∴DE===2,
∴EC=DC-DE=4-2.
(2)S阴影=S扇形FAE-S△ADE=-×2×2=π-2.
11.如图3-11-10,AB是⊙O的直径,弦CD交AB于点E,OF⊥AC于点F.
(1)请探索OF和BC的关系并说明理由;
(2)若∠D=30°,BC=1时,求圆中阴影部分的面积.
图3-11-10
解:(1)OF∥BC,OF=BC.
理由:由垂径定理得AF=CF.
∵AO=BO,
∴OF是△ABC的中位线.
∴OF∥BC,OF=BC.
(2)连结OC,由(1)知OF=.
∵AB是⊙O的直径,∴∠ACB=90°.
∵∠D=30°,∴∠A=30°.
∴AB=2BC=2,∴AC=,
∴S△AOC=×AC×OF=.
∵∠AOC=120°,OA=1,
∴S扇形AOC==.
∴S阴影=S扇形AOC-S△AOC=-.
12.如图3-11-11,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠1=∠C(∠1是指∠PBC).
(1)求证:CB∥PD;
(2)若∠1=22.5°,⊙O的半径R=2,求劣弧AC的长度.
图3-11-11
解:(1)证明:∵P,C,B,D,四点共圆,
第12题答图
∴∠1=∠CDP.
∵∠1=∠C,
∴∠C=∠CDP,
∴CB∥PD.
(2)如答图,连结OC,OD,BD,
∵CD⊥AB,且AB是直径,
∴∠BCD=∠BDC=∠1=22.5°,
∴∠BOC=2∠BDC=45°,
∴∠AOC=135°,
∴弧AC的长度为==π.
【思维升华】
13.如图3-11-12,在Rt△OAB中,∠AOB=30°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为__π__.
图3-11-12
【解析】
∵Rt△OAB中,∠AOB=30°,AB=2,
∴AO=CO=2,BO=DO=4,
∴阴影部分面积=S扇形BOD+S△AOB-S扇形AOC-S△COD=S扇形BOD-S扇形AOC
=-=π.
14.如图3-11-13,在正方形ABCD中,AD=2,E是
AB的中点,将△BEC绕点B逆时针旋转90°后,点E
落在CB的延长线上点F处,点C落在点A处.再将线
段AF绕点F顺时针旋转90°得线段FG,连结EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.
解:(1)证明:∵四边形ABCD是正方形,
∴AB=BC=AD=2,
∠ABC=90°.
∵△BEC绕点B逆时针旋转90°得△ABF,
∴△ABF≌△CBE,
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,
AF=EC,
∴∠AFB+∠FAB=90°.
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,AF=FG,
∴∠CFG=∠FAB=∠ECB,
∴EC∥FG.
∵AF=EC,AF=FG,
∴EC=FG,
∴四边形EFGC是平行四边形,
∴EF∥CG.
(2)∵△ABF≌△CBE,
∴FB=BE=AB=1,
∴AF==.
在△FEC和△CGF中,
∵EC=FG,∠ECF=∠GFC,FC=CF,
∴△FEC≌△CGF,
∴S△FEC=S△CGF,
∴S阴影=S扇形ABC+S△ABF+S△FGC-S扇形AFG
=+×2×1+×(1+2)×1-
=-.
第9题答图
图3-11-9
图3-11-13
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
