北京版五年级数学下6.1露在外面的面 课件(21页PPT)
文档属性
| 名称 | 北京版五年级数学下6.1露在外面的面 课件(21页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 12:31:32 | ||
图片预览






文档简介
一、复习
正方体
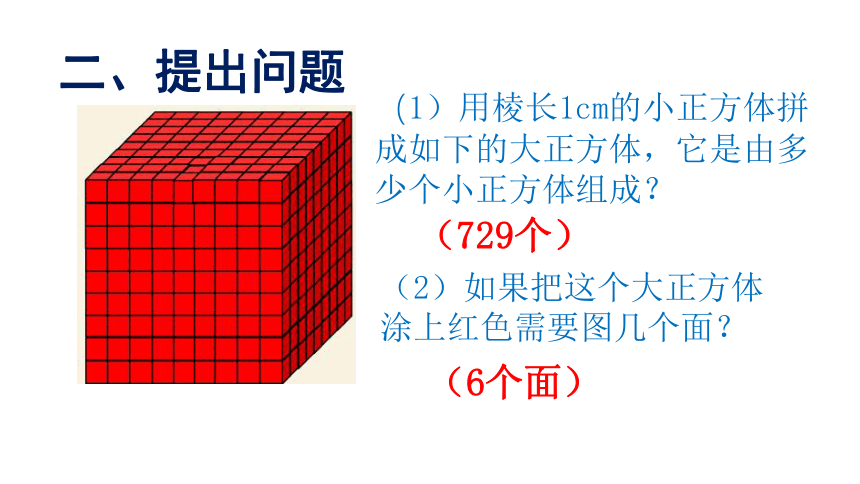
(1)用棱长1cm的小正方体拼成如下的大正方体,它是由多少个小正方体组成?
(729个)
(2)如果把这个大正方体涂上红色需要图几个面?
(6个面)
二、提出问题
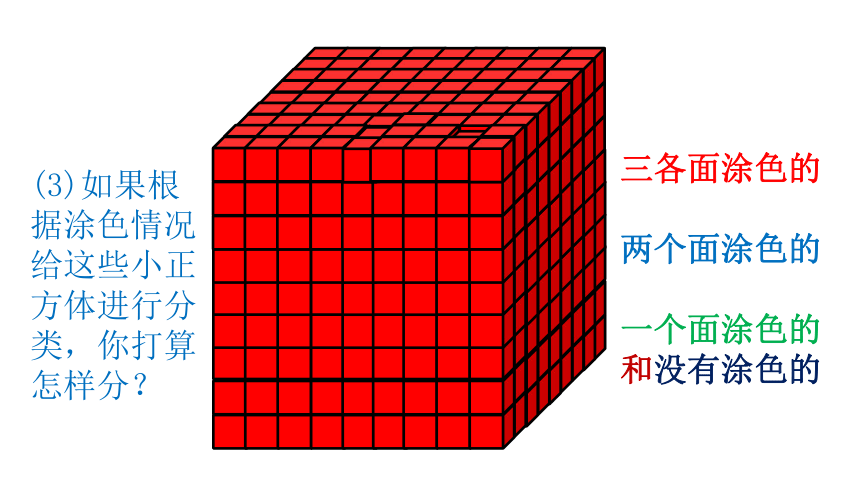
(3)如果根据涂色情况给这些小正方体进行分类,你打算怎样分?
三各面涂色的
两个面涂色的
一个面涂色的
和没有涂色的
用棱长1cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
三、化繁为简,寻找规律
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
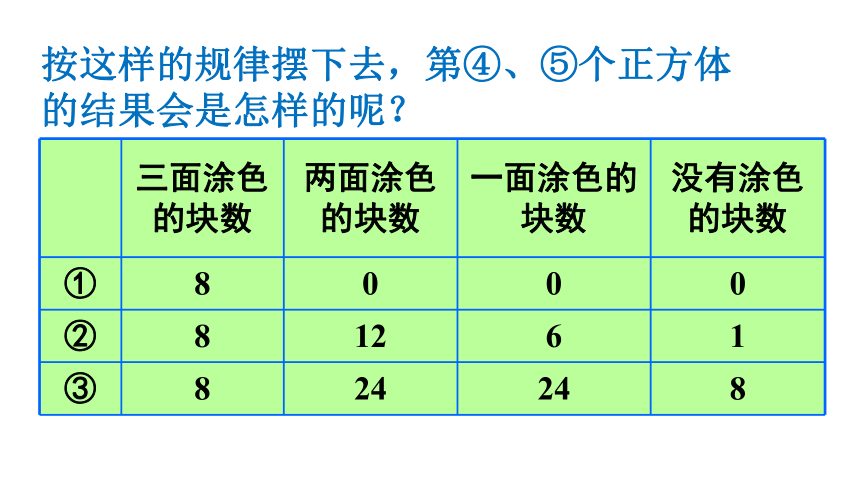
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
①
8
0
0
0
②
8
12
6
1
③
8
24
24
8
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
?
8
0
0
0
?
8
12
6
1
?
8
24
24
8
?
?
8
36
54
27
8
48
96
64
①
②
③
④
⑤
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
四、发现规律
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
没有涂色
没有土色的块数是:
(n-2)×(n-2)×(n-2)
五、应有规律,解决问题
1.下图中,三面涂色、两面涂色、一面涂色和没有涂色的各有多少个?
三面涂色:
8个
两面涂色:
(9-2)×12
=7×12
﹦84(个)
一面涂色:
(9-2)×(9-2)×6
=49×6
=294(个)
没有涂色:
(9-2)×(9-2)×9-2)
=49×7
=343(个)
9
9
9
4
10
20
第一层:1
第二层:1+2
4=1+(1+2)
第一层:1
第二层:1+2
10=1+(1+2)+(1+2+3)
第三层:1+2+3
……
……
2.如果摆成下面的几何体你能数吗?
六、课堂小结
通过这节课的学习,你有什么收获?
正方体
(1)用棱长1cm的小正方体拼成如下的大正方体,它是由多少个小正方体组成?
(729个)
(2)如果把这个大正方体涂上红色需要图几个面?
(6个面)
二、提出问题
(3)如果根据涂色情况给这些小正方体进行分类,你打算怎样分?
三各面涂色的
两个面涂色的
一个面涂色的
和没有涂色的
用棱长1cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
三、化繁为简,寻找规律
用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①、②、③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
①
②
③
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
①
8
0
0
0
②
8
12
6
1
③
8
24
24
8
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
三面涂色的块数
两面涂色的块数
一面涂色的块数
没有涂色的块数
?
8
0
0
0
?
8
12
6
1
?
8
24
24
8
?
?
8
36
54
27
8
48
96
64
①
②
③
④
⑤
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
四、发现规律
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
没有涂色
没有土色的块数是:
(n-2)×(n-2)×(n-2)
五、应有规律,解决问题
1.下图中,三面涂色、两面涂色、一面涂色和没有涂色的各有多少个?
三面涂色:
8个
两面涂色:
(9-2)×12
=7×12
﹦84(个)
一面涂色:
(9-2)×(9-2)×6
=49×6
=294(个)
没有涂色:
(9-2)×(9-2)×9-2)
=49×7
=343(个)
9
9
9
4
10
20
第一层:1
第二层:1+2
4=1+(1+2)
第一层:1
第二层:1+2
10=1+(1+2)+(1+2+3)
第三层:1+2+3
……
……
2.如果摆成下面的几何体你能数吗?
六、课堂小结
通过这节课的学习,你有什么收获?
