五年级数学上册课件 2.7 不规则图形的面积 2021-2022学年苏教版(18页PPT )
文档属性
| 名称 | 五年级数学上册课件 2.7 不规则图形的面积 2021-2022学年苏教版(18页PPT ) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 13:33:13 | ||
图片预览



文档简介
第8课时 不规则图形的面积
苏教版数学五年级上册
多边形的面积
1.掌握用数方格的方法估计不规则图形的面积,了解不同的数法得到的结果与实际面积的差异情况。
2.通过估计不规则图形的面积,了解不规则图形面积的不同估计方法,感受不规则图形的面积的取值范围,初步体会逐渐逼近的极限思想。
【重点】掌握用数方格的方法估计不规则图形的面积。
【难点】理解不同估计方法和面积大小的取值范围。
学习目标
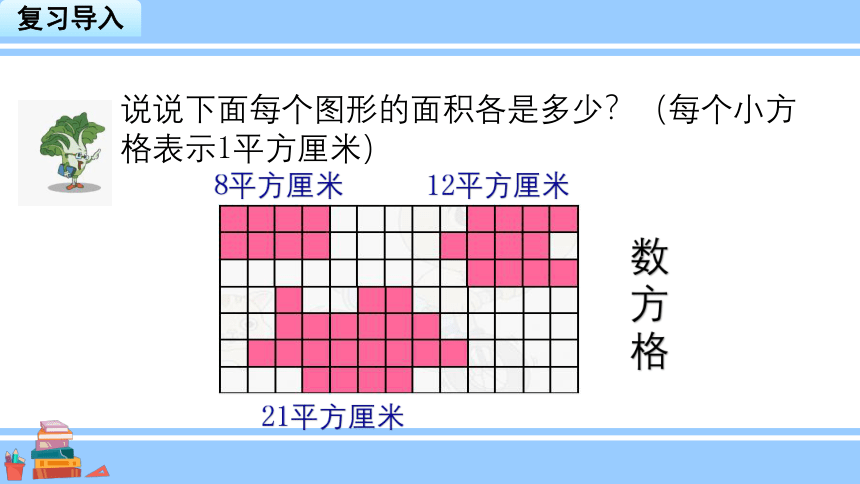
说说下面每个图形的面积各是多少?(每个小方格表示1平方厘米)
复习导入
你知道这条蜿蜒曲折的湖泊的占地面积是怎么估算出来的吗?
11
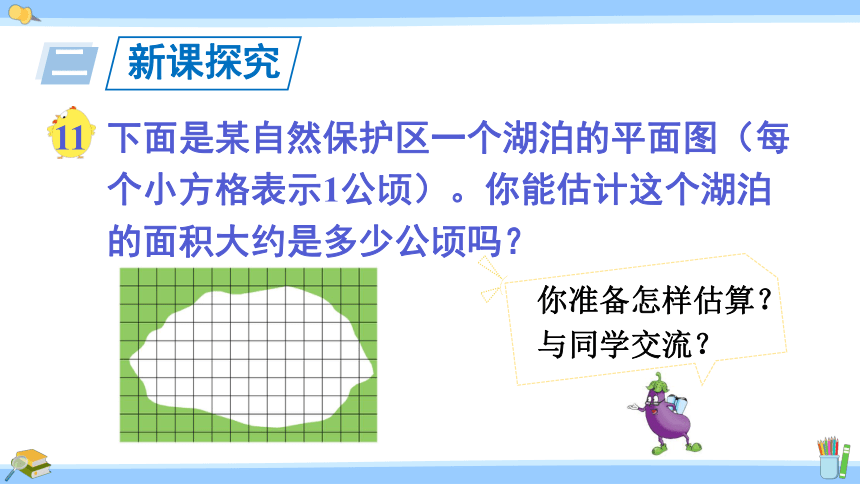
下面是某自然保护区一个湖泊的平面图(每个小方格表示1公顷)。你能估计这个湖泊的面积大约是多少公顷吗?
你准备怎样估算?与同学交流?
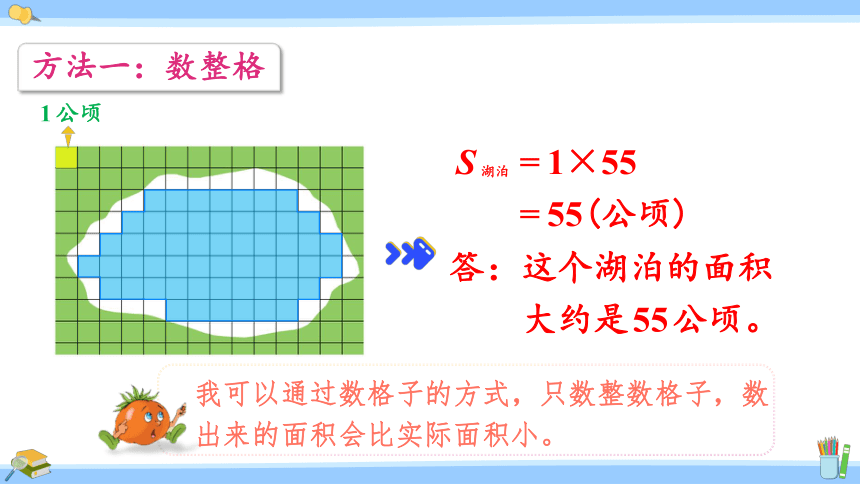
方法一:数整格
我可以通过数格子的方式,只数整数格子,数出来的面积会比实际面积小。
1公顷
S
湖泊
=1×55
=55(公顷)
答:这个湖泊的面积
大约是55公顷。
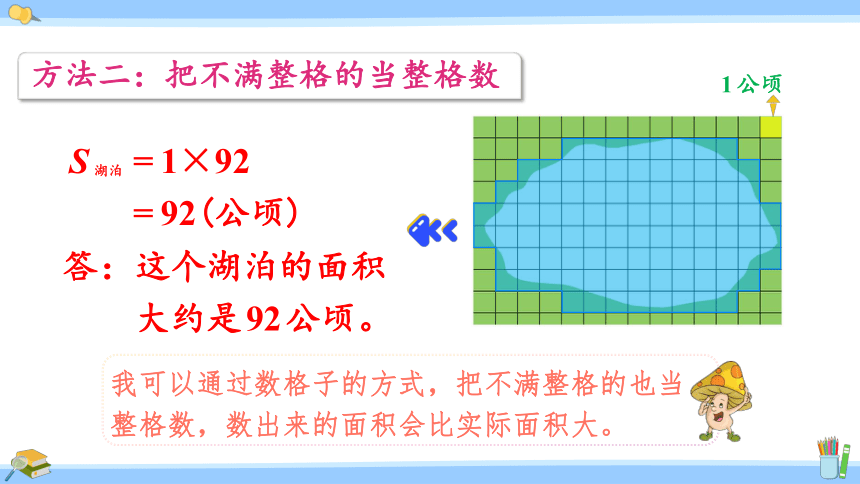
方法二:把不满整格的当整格数
我可以通过数格子的方式,把不满整格的也当整格数,数出来的面积会比实际面积大。
1公顷
S
湖泊
=1×92
=92(公顷)
答:这个湖泊的面积
大约是92公顷。
方法三:把不满整格的当半格算
1公顷
我可以通过数格子的方式,把不满整格当半格数,数出来的面积会更接近实际面积。
S
湖泊
=1×55+1×36÷2
=55+18=73(公顷)
答:这个湖泊的面积
大约是73公顷。
选择一种方法数一数,与同学比较数的结果。
只数整格,数出的结果比实际面积小。
把半格当整格来算,数出的结果比实际面积大。
把半格当半格算,数出的结果最接近实际面积。
在数方格估算不则图形的面积,技巧在于:
按照一定的顺序数,可以从上到下,也可以从左到右一格一格的数,为了避免数错或数漏,在数的同时可以做上标记,也可以打“√”。
估计一下,图中树叶的面积大约是多少平方厘米?(每个小方格表示1平方厘米)
解:
整格的:22格
不满整格的:34格
22+34÷2=39(cm?)
答:图中树叶的面积大约是39平方厘米。
2. 先在方格纸上描出自己手掌的轮廓线,再用数
方格的方法估计自己手掌的面积大约是多少平
方厘米。
解:
整格的:43格
不满整格的:26格
43+26÷2=56(cm?)
答:手掌的面积大约是56平方厘米。
张叔叔想租用如图所示的池塘养鱼,平均每平方米年租金为5元,估一估,这一年他应付租金约多少元?(每小方格的边长表示10米)
解:
整格的:25格
不满整格的:18格
答:这一年他应付租金约17000元。
S
池塘
=(25+18÷2)×10
=3400(m?)
3400×5=17000(元)
2. 下面的2个大正方形的边长都是10厘米,先计
算每个大正方形中小方格的面积,再估算笑
脸的面积。
解:
答:上面的笑脸面积约是26平方厘米,
下面的笑脸面积约是28平方厘米。
10×10÷100=1(cm?)
10×10÷25=4(cm?)
上面:(16+20÷2)×1=26(cm?)
下面:(2+10÷2)×4=28(cm?)
每个正方形的面积:120÷6=20(平方米),图形B里面有7个整格和8个半格,图形B的面积:20×7+(8÷2×20)=220(平方米);
图形C里面有12个整格和17个半格,它的面积是:20×12+(17÷2×20)=410(平方米);
410
220
3.图中图形A的面积是120平方米,则:图形B的面积是( ) 平方米;图形C的面积大约是( )平方米(填整数)。
估计不规则图形的面积方法:
有些图形不是由几个简单的图形组成的,我们可以在方格纸中估计它的面积。估计时,先数整格的,再数不满整格的,不满整格的按半格计算。
苏教版数学五年级上册
多边形的面积
1.掌握用数方格的方法估计不规则图形的面积,了解不同的数法得到的结果与实际面积的差异情况。
2.通过估计不规则图形的面积,了解不规则图形面积的不同估计方法,感受不规则图形的面积的取值范围,初步体会逐渐逼近的极限思想。
【重点】掌握用数方格的方法估计不规则图形的面积。
【难点】理解不同估计方法和面积大小的取值范围。
学习目标
说说下面每个图形的面积各是多少?(每个小方格表示1平方厘米)
复习导入
你知道这条蜿蜒曲折的湖泊的占地面积是怎么估算出来的吗?
11
下面是某自然保护区一个湖泊的平面图(每个小方格表示1公顷)。你能估计这个湖泊的面积大约是多少公顷吗?
你准备怎样估算?与同学交流?
方法一:数整格
我可以通过数格子的方式,只数整数格子,数出来的面积会比实际面积小。
1公顷
S
湖泊
=1×55
=55(公顷)
答:这个湖泊的面积
大约是55公顷。
方法二:把不满整格的当整格数
我可以通过数格子的方式,把不满整格的也当整格数,数出来的面积会比实际面积大。
1公顷
S
湖泊
=1×92
=92(公顷)
答:这个湖泊的面积
大约是92公顷。
方法三:把不满整格的当半格算
1公顷
我可以通过数格子的方式,把不满整格当半格数,数出来的面积会更接近实际面积。
S
湖泊
=1×55+1×36÷2
=55+18=73(公顷)
答:这个湖泊的面积
大约是73公顷。
选择一种方法数一数,与同学比较数的结果。
只数整格,数出的结果比实际面积小。
把半格当整格来算,数出的结果比实际面积大。
把半格当半格算,数出的结果最接近实际面积。
在数方格估算不则图形的面积,技巧在于:
按照一定的顺序数,可以从上到下,也可以从左到右一格一格的数,为了避免数错或数漏,在数的同时可以做上标记,也可以打“√”。
估计一下,图中树叶的面积大约是多少平方厘米?(每个小方格表示1平方厘米)
解:
整格的:22格
不满整格的:34格
22+34÷2=39(cm?)
答:图中树叶的面积大约是39平方厘米。
2. 先在方格纸上描出自己手掌的轮廓线,再用数
方格的方法估计自己手掌的面积大约是多少平
方厘米。
解:
整格的:43格
不满整格的:26格
43+26÷2=56(cm?)
答:手掌的面积大约是56平方厘米。
张叔叔想租用如图所示的池塘养鱼,平均每平方米年租金为5元,估一估,这一年他应付租金约多少元?(每小方格的边长表示10米)
解:
整格的:25格
不满整格的:18格
答:这一年他应付租金约17000元。
S
池塘
=(25+18÷2)×10
=3400(m?)
3400×5=17000(元)
2. 下面的2个大正方形的边长都是10厘米,先计
算每个大正方形中小方格的面积,再估算笑
脸的面积。
解:
答:上面的笑脸面积约是26平方厘米,
下面的笑脸面积约是28平方厘米。
10×10÷100=1(cm?)
10×10÷25=4(cm?)
上面:(16+20÷2)×1=26(cm?)
下面:(2+10÷2)×4=28(cm?)
每个正方形的面积:120÷6=20(平方米),图形B里面有7个整格和8个半格,图形B的面积:20×7+(8÷2×20)=220(平方米);
图形C里面有12个整格和17个半格,它的面积是:20×12+(17÷2×20)=410(平方米);
410
220
3.图中图形A的面积是120平方米,则:图形B的面积是( ) 平方米;图形C的面积大约是( )平方米(填整数)。
估计不规则图形的面积方法:
有些图形不是由几个简单的图形组成的,我们可以在方格纸中估计它的面积。估计时,先数整格的,再数不满整格的,不满整格的按半格计算。
