冀教版七年级下册数学 7.7相交线与平行线 回顾与反思 教案
文档属性
| 名称 | 冀教版七年级下册数学 7.7相交线与平行线 回顾与反思 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 19:56:10 | ||
图片预览



文档简介
相交线与平行线知识点整理
教学目标
??知识技能:了解本单元的知识点及其之间的关系;理解对顶角相等和垂线的性质;掌握平行线的判定和性质;了解命题、真命题、假命题及定理的含义,理解平移的基本性质.
??数学思考:在参与猜想、观察、实验、综合实践等活动的过程中,发展说理,初步推理和语言表达能力;初步形成从特殊到一般的思维方式,了解数学知识是来源于实践,应用于实践的,了解数形结合思想,数学建模思想.
??情感态度:认识数学严谨、抽象和应用广泛的特点,体会数学的应用价值. 激发学习图形与几何的兴趣.
二、重难点分析
??教学重点:掌握本单元知识体系,理解各知识点之间的关联,会利用相交线和平行线的有关定理解决问题.
??本节课要对本单元的知识结构进行梳理,使学生了解本单元的知识体系,以及本单元知识与其他单元知识的联系.
??教学难点:灵活应用本单元知识解题,会将本单元知识与其他单元知识综合运用.
相交线
1、邻补角与对顶角
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
图形 顶点 边的关系 大小关系
对顶角
∠1与∠2 有公共顶点 ∠1的两边与∠2的两边互为反向延长线 对顶角相等
即∠1=∠2
邻补角
∠3与∠4 有公共顶点 ∠3与∠4有一条边公共,另一边互为反向延长线。 ∠3+∠4=180°
注意点:⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角
⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2、垂线
⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:
如图所示:AB⊥CD,垂足为O
⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)
⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
3、垂线的画法:
⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4、点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
记得时候应该结合图形进行记忆。
如图,PO⊥AB,同P到直线AB的距离是PO的长。PO是垂线段。PO是点P到直线AB所有线段中最短的一条。
现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用。
5、如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念
分析它们的联系与区别
⑴垂线与垂线段 区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。 联系:具有垂直于已知直线的共同特征。(垂直的性质)
⑵两点间距离与点到直线的距离 区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间。 联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离。
⑶线段与距离 距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
平行线
1、平行线的概念:
在同一平面内,不相交的两条直线叫做平行线,直线与直线互相平行,记作∥。
2、两条直线的位置关系
在同一平面内,两条直线的位置关系只有两种:⑴相交;⑵平行。
因此当我们得知在同一平面内两直线不相交时,就可以肯定它们平行;反过来也一样(这里,我们把重合的两直线看成一条直线)
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合(因为两点确定一条直线)
3、平行公理――平行线的存在性与惟一性
经过直线外一点,有且只有一条直线与这条直线平行
4、平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
如左图所示,∵∥,∥
∴∥
注意符号语言书写,前提条件是两直线都平行于第三条直线,才会结论,这两条直线都平行。
5、三线八角
两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角。
如图,直线被直线所截
①∠1与∠5在截线的同侧,同在被截直线的上方,
叫做同位角(位置相同)
②∠5与∠3在截线的两旁(交错),在被截直线之间(内),叫做内错角(位置在内且交错)
③∠5与∠4在截线的同侧,在被截直线之间(内),叫做同旁内角。
④三线八角也可以成模型中看出。同位角是“A”型;内错角是“Z”型;同旁内角是“U”型。
6、如何判别三线八角
判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”,有时需要将有关的部分“抽出”或把无关的线略去不看,有时又需要把图形补全。
例如:
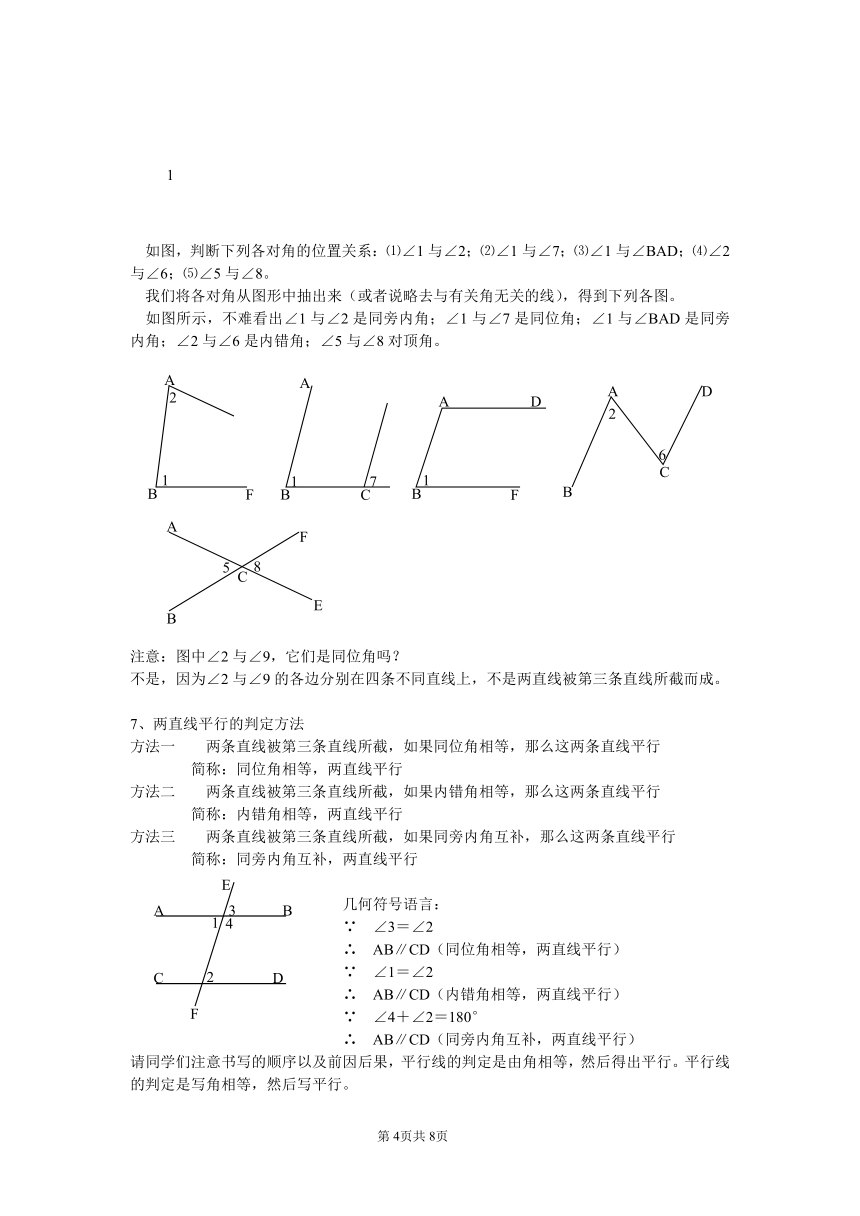
如图,判断下列各对角的位置关系:⑴∠1与∠2;⑵∠1与∠7;⑶∠1与∠BAD;⑷∠2与∠6;⑸∠5与∠8。
我们将各对角从图形中抽出来(或者说略去与有关角无关的线),得到下列各图。
如图所示,不难看出∠1与∠2是同旁内角;∠1与∠7是同位角;∠1与∠BAD是同旁内角;∠2与∠6是内错角;∠5与∠8对顶角。
注意:图中∠2与∠9,它们是同位角吗?
不是,因为∠2与∠9的各边分别在四条不同直线上,不是两直线被第三条直线所截而成。
7、两直线平行的判定方法
方法一 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
简称:同位角相等,两直线平行
方法二 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简称:内错角相等,两直线平行
方法三 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简称:同旁内角互补,两直线平行
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
请同学们注意书写的顺序以及前因后果,平行线的判定是由角相等,然后得出平行。平行线的判定是写角相等,然后写平行。
注意:⑴几何中,图形之间的“位置关系”一般都与某种“数量关系”有着内在的联系,常由“位置关系”决定其“数量关系”,反之也可从“数量关系”去确定“位置关系”。上述平行线的判定方法就是根据同位角或内错角“相等”或同旁内角“互补”这种“数量关系”,判定两直线“平行”这种“位置关系”。
⑵根据平行线的定义和平行公理的推论,平行线的判定方法还有两种:①如果两条直线没有交点(不相交),那么两直线平行。②如果两条直线都平行于第三条直线,那么这两条直线平行。
典型例题:判断下列说法是否正确,如果不正确,请给予改正:
⑴不相交的两条直线必定平行线。
⑵在同一平面内不相重合的两条直线,如果它们不平行,那么这两条直线一定相交。
⑶过一点可以且只可以画一条直线与已知直线平行
解答:⑴错误,平行线是“在同一平面内不相交的两条直线”。“在同一平面内”是一项重要条件,不能遗漏。
⑵正确
⑶不正确,正确的说法是“过直线外一点”而不是“过一点”。因为如果这一点不在已知直线上,是作不出这条直线的平行线的。
典型例题:如图,根据下列条件,可以判定哪两条直线平行,并说明判定的根据是什么?
解答:⑴由∠2=∠B可判定AB∥DE,根据是同位角相等,两直线平行;
⑵由∠1=∠D可判定AC∥DF,根据是内错角相等,两直线平行;
⑶由∠3+∠F=180°可判定AC∥DF,根据同旁内角互补,两直线平行。
平行线的性质
1、平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补。
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
2、两条平行线的距离
如图,直线AB∥CD,EF⊥AB于E,EF⊥CD于F,则称线段EF的长度为两平行线AB与CD间的距离。
注意:直线AB∥CD,在直线AB上任取一点G,过点G作CD的垂线段GH,则垂线段GH的长度也就是直线AB与CD间的距离。
3、命题:
⑴命题的概念:
判断一件事情的语句,叫做命题。
⑵命题的组成
每个命题都是题设、结论两部分组成。题设是已知事项;结论是由已知事项推出的事项。命题常写成“如果……,那么……”的形式。具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论。
有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显。对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式。
注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述。
4、平行线的性质与判定
①平行线的性质与判定是互逆的关系
两直线平行 同位角相等;
两直线平行 内错角相等;
两直线平行 同旁内角互补。
其中,由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质。
典型例题:已知∠1=∠B,求证:∠2=∠C
证明:∵∠1=∠B(已知)
∴DE∥BC(同位角相等,
两直线平行)
∴∠2=∠C(两直线平行
同位角相等)
注意,在了DE∥BC,不需要再写一次了,得到了DE∥BC,这可以把它当作条件来用了。
典型例题:如图,AB∥DF,DE∥BC,∠1=65°
求∠2、∠3的度数
解答:∵DE∥BC(已知)
∴∠2=∠1=65°(两直线平行,内错角相等)
∵AB∥DF(已知)
∴AB∥DF(已知)
∴∠3+∠2=180°(两直线平行,同旁内角互补)
∴∠3=180°-∠2=180°-65°=115°
平移
1、平移变换
①把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同。
②新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点
③连接各组对应点的线段平行且相等
2、平移的特征:
①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化。
②经过平移后,对应点所连的线段平行(或在同一直线上)且相等。
典型例题:如图,△ABC经过平移之后成为△DEF,那么:
⑴点A的对应点是点_________;⑵点B的对应点是点______。
⑶点_____的对应点是点F;⑷线段AB的对应线段是线段_______;
⑸线段BC的对应线段是线段_______;⑹∠A的对应角是______。
⑺____的对应角是∠F。
解答:
⑴D;⑵E;⑶C;⑷DE;⑸EF;⑹∠D;⑺∠ACB。
思维方式:利用平移特征:平移前后对应线段相等,对应点的连线段平行或在同一直线上解答。
第1页共8页
教学目标
??知识技能:了解本单元的知识点及其之间的关系;理解对顶角相等和垂线的性质;掌握平行线的判定和性质;了解命题、真命题、假命题及定理的含义,理解平移的基本性质.
??数学思考:在参与猜想、观察、实验、综合实践等活动的过程中,发展说理,初步推理和语言表达能力;初步形成从特殊到一般的思维方式,了解数学知识是来源于实践,应用于实践的,了解数形结合思想,数学建模思想.
??情感态度:认识数学严谨、抽象和应用广泛的特点,体会数学的应用价值. 激发学习图形与几何的兴趣.
二、重难点分析
??教学重点:掌握本单元知识体系,理解各知识点之间的关联,会利用相交线和平行线的有关定理解决问题.
??本节课要对本单元的知识结构进行梳理,使学生了解本单元的知识体系,以及本单元知识与其他单元知识的联系.
??教学难点:灵活应用本单元知识解题,会将本单元知识与其他单元知识综合运用.
相交线
1、邻补角与对顶角
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
图形 顶点 边的关系 大小关系
对顶角
∠1与∠2 有公共顶点 ∠1的两边与∠2的两边互为反向延长线 对顶角相等
即∠1=∠2
邻补角
∠3与∠4 有公共顶点 ∠3与∠4有一条边公共,另一边互为反向延长线。 ∠3+∠4=180°
注意点:⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角
⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2、垂线
⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:
如图所示:AB⊥CD,垂足为O
⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)
⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
3、垂线的画法:
⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4、点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
记得时候应该结合图形进行记忆。
如图,PO⊥AB,同P到直线AB的距离是PO的长。PO是垂线段。PO是点P到直线AB所有线段中最短的一条。
现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用。
5、如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念
分析它们的联系与区别
⑴垂线与垂线段 区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。 联系:具有垂直于已知直线的共同特征。(垂直的性质)
⑵两点间距离与点到直线的距离 区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间。 联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离。
⑶线段与距离 距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
平行线
1、平行线的概念:
在同一平面内,不相交的两条直线叫做平行线,直线与直线互相平行,记作∥。
2、两条直线的位置关系
在同一平面内,两条直线的位置关系只有两种:⑴相交;⑵平行。
因此当我们得知在同一平面内两直线不相交时,就可以肯定它们平行;反过来也一样(这里,我们把重合的两直线看成一条直线)
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合(因为两点确定一条直线)
3、平行公理――平行线的存在性与惟一性
经过直线外一点,有且只有一条直线与这条直线平行
4、平行公理的推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
如左图所示,∵∥,∥
∴∥
注意符号语言书写,前提条件是两直线都平行于第三条直线,才会结论,这两条直线都平行。
5、三线八角
两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角。
如图,直线被直线所截
①∠1与∠5在截线的同侧,同在被截直线的上方,
叫做同位角(位置相同)
②∠5与∠3在截线的两旁(交错),在被截直线之间(内),叫做内错角(位置在内且交错)
③∠5与∠4在截线的同侧,在被截直线之间(内),叫做同旁内角。
④三线八角也可以成模型中看出。同位角是“A”型;内错角是“Z”型;同旁内角是“U”型。
6、如何判别三线八角
判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”,有时需要将有关的部分“抽出”或把无关的线略去不看,有时又需要把图形补全。
例如:
如图,判断下列各对角的位置关系:⑴∠1与∠2;⑵∠1与∠7;⑶∠1与∠BAD;⑷∠2与∠6;⑸∠5与∠8。
我们将各对角从图形中抽出来(或者说略去与有关角无关的线),得到下列各图。
如图所示,不难看出∠1与∠2是同旁内角;∠1与∠7是同位角;∠1与∠BAD是同旁内角;∠2与∠6是内错角;∠5与∠8对顶角。
注意:图中∠2与∠9,它们是同位角吗?
不是,因为∠2与∠9的各边分别在四条不同直线上,不是两直线被第三条直线所截而成。
7、两直线平行的判定方法
方法一 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
简称:同位角相等,两直线平行
方法二 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
简称:内错角相等,两直线平行
方法三 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
简称:同旁内角互补,两直线平行
几何符号语言:
∵ ∠3=∠2
∴ AB∥CD(同位角相等,两直线平行)
∵ ∠1=∠2
∴ AB∥CD(内错角相等,两直线平行)
∵ ∠4+∠2=180°
∴ AB∥CD(同旁内角互补,两直线平行)
请同学们注意书写的顺序以及前因后果,平行线的判定是由角相等,然后得出平行。平行线的判定是写角相等,然后写平行。
注意:⑴几何中,图形之间的“位置关系”一般都与某种“数量关系”有着内在的联系,常由“位置关系”决定其“数量关系”,反之也可从“数量关系”去确定“位置关系”。上述平行线的判定方法就是根据同位角或内错角“相等”或同旁内角“互补”这种“数量关系”,判定两直线“平行”这种“位置关系”。
⑵根据平行线的定义和平行公理的推论,平行线的判定方法还有两种:①如果两条直线没有交点(不相交),那么两直线平行。②如果两条直线都平行于第三条直线,那么这两条直线平行。
典型例题:判断下列说法是否正确,如果不正确,请给予改正:
⑴不相交的两条直线必定平行线。
⑵在同一平面内不相重合的两条直线,如果它们不平行,那么这两条直线一定相交。
⑶过一点可以且只可以画一条直线与已知直线平行
解答:⑴错误,平行线是“在同一平面内不相交的两条直线”。“在同一平面内”是一项重要条件,不能遗漏。
⑵正确
⑶不正确,正确的说法是“过直线外一点”而不是“过一点”。因为如果这一点不在已知直线上,是作不出这条直线的平行线的。
典型例题:如图,根据下列条件,可以判定哪两条直线平行,并说明判定的根据是什么?
解答:⑴由∠2=∠B可判定AB∥DE,根据是同位角相等,两直线平行;
⑵由∠1=∠D可判定AC∥DF,根据是内错角相等,两直线平行;
⑶由∠3+∠F=180°可判定AC∥DF,根据同旁内角互补,两直线平行。
平行线的性质
1、平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补。
几何符号语言:
∵AB∥CD
∴∠1=∠2(两直线平行,内错角相等)
∵AB∥CD
∴∠3=∠2(两直线平行,同位角相等)
∵AB∥CD
∴∠4+∠2=180°(两直线平行,同旁内角互补)
2、两条平行线的距离
如图,直线AB∥CD,EF⊥AB于E,EF⊥CD于F,则称线段EF的长度为两平行线AB与CD间的距离。
注意:直线AB∥CD,在直线AB上任取一点G,过点G作CD的垂线段GH,则垂线段GH的长度也就是直线AB与CD间的距离。
3、命题:
⑴命题的概念:
判断一件事情的语句,叫做命题。
⑵命题的组成
每个命题都是题设、结论两部分组成。题设是已知事项;结论是由已知事项推出的事项。命题常写成“如果……,那么……”的形式。具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论。
有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显。对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式。
注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述。
4、平行线的性质与判定
①平行线的性质与判定是互逆的关系
两直线平行 同位角相等;
两直线平行 内错角相等;
两直线平行 同旁内角互补。
其中,由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质。
典型例题:已知∠1=∠B,求证:∠2=∠C
证明:∵∠1=∠B(已知)
∴DE∥BC(同位角相等,
两直线平行)
∴∠2=∠C(两直线平行
同位角相等)
注意,在了DE∥BC,不需要再写一次了,得到了DE∥BC,这可以把它当作条件来用了。
典型例题:如图,AB∥DF,DE∥BC,∠1=65°
求∠2、∠3的度数
解答:∵DE∥BC(已知)
∴∠2=∠1=65°(两直线平行,内错角相等)
∵AB∥DF(已知)
∴AB∥DF(已知)
∴∠3+∠2=180°(两直线平行,同旁内角互补)
∴∠3=180°-∠2=180°-65°=115°
平移
1、平移变换
①把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同。
②新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点
③连接各组对应点的线段平行且相等
2、平移的特征:
①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化。
②经过平移后,对应点所连的线段平行(或在同一直线上)且相等。
典型例题:如图,△ABC经过平移之后成为△DEF,那么:
⑴点A的对应点是点_________;⑵点B的对应点是点______。
⑶点_____的对应点是点F;⑷线段AB的对应线段是线段_______;
⑸线段BC的对应线段是线段_______;⑹∠A的对应角是______。
⑺____的对应角是∠F。
解答:
⑴D;⑵E;⑶C;⑷DE;⑸EF;⑹∠D;⑺∠ACB。
思维方式:利用平移特征:平移前后对应线段相等,对应点的连线段平行或在同一直线上解答。
第1页共8页
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
