陕西省师大附中2012届高三高考模拟试题数学理
文档属性
| 名称 | 陕西省师大附中2012届高三高考模拟试题数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 271.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-10 21:04:39 | ||
图片预览


文档简介
陕西师大附中高2012届高考数学(理)模拟试题
一、选择题(本大题共10题,每小题5分,共50分)
1.若集合,,且,则实数的取值范围为【 】.
A. B. C. D.
2.经问卷调查,某班学生对摄影分别持“喜欢”、“不喜欢”和“一般”三种态度,其中持“一般”态度的学生比持“不喜欢”的学生多人,按分层抽样的方法(抽样过程中不需要剔除个体)从全班选出部分学生进行关于摄影的座谈.若抽样得出的位同学中有位持“喜欢”态度的同学,位持“不喜欢”态度的同学和位持“一般”态度的同学,则全班持“喜欢”态度的同学人数为【 】.
A. B. C. D.
3.函数是【 】.
A.偶函数,在区间上单调递增 B.偶函数,在区间上单调递减
C.奇函数,在区间上单调递增 D.奇函数,在区间上单调递减
4.若圆锥的主视图(正视图)是一个边长为的等边三角形,则该圆锥的表面积为【 】.
A. B. C. D.
5.若数列是等差数列,则数列也为等差数列.类比这一性质可知,若正项数列是等比数列,且也是等比数列,则的表达式应为【 】.
A. B.
C. D.
6.若双曲线的一个焦点与抛物线的焦点相同,且双曲线的离心率为,则该双曲线的方程为【 】.
A. B. C. D.
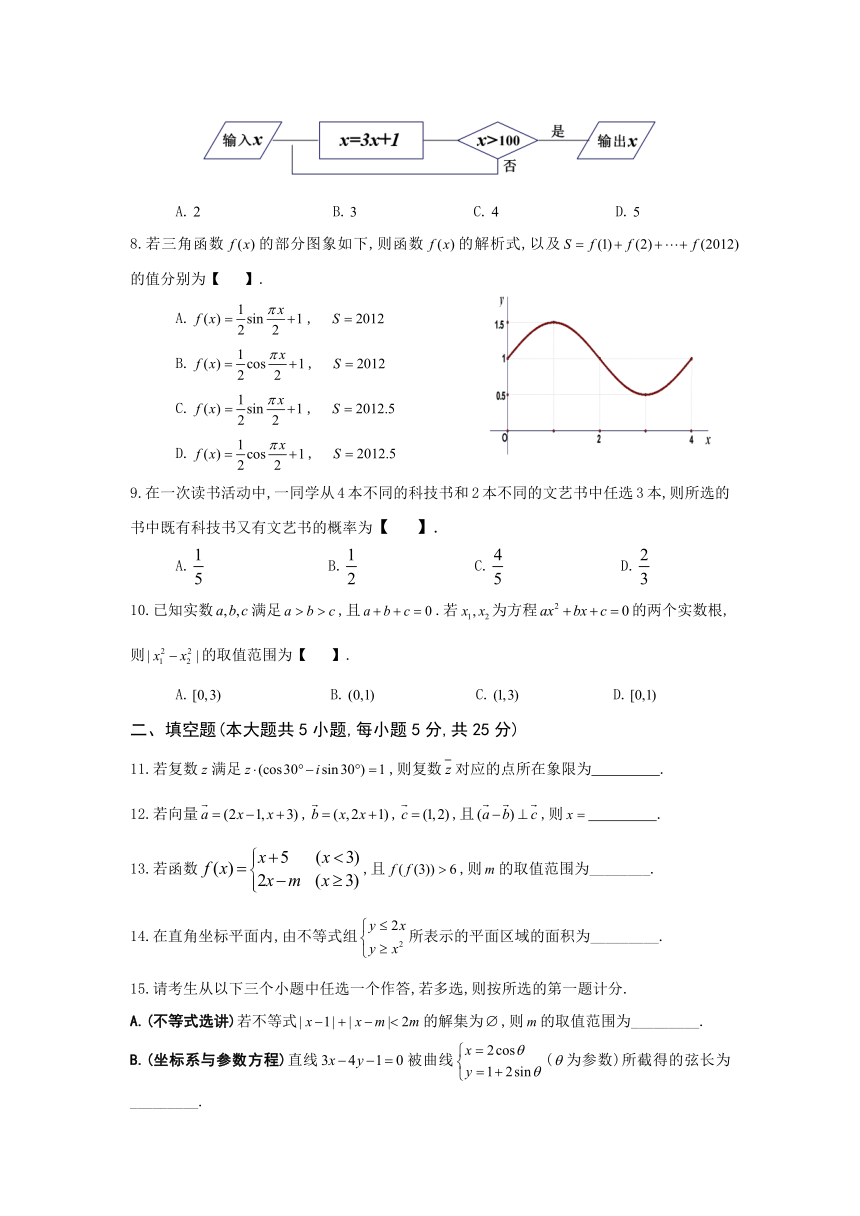
7.按下面的流程图进行计算.若输出的,则输入的正实数值的个数最多为【 】.
A. B. C. D.
8.若三角函数的部分图象如下,则函数的解析式,以及的值分别为【 】.
A.,
B.,
C.,
D.,
9.在一次读书活动中,一同学从4本不同的科技书和2本不同的文艺书中任选3本,则所选的书中既有科技书又有文艺书的概率为【 】.
A. B. C. D.
10.已知实数满足,且.若为方程的两个实数根,则的取值范围为【 】.
A. B. C. D.
二、填空题(本大题共5小题,每小题5分,共25分)
11.若复数满足,则复数对应的点所在象限为 .
12.若向量,,,且,则 .
13.若函数,且,则的取值范围为________.
14.在直角坐标平面内,由不等式组所表示的平面区域的面积为_________.
15.请考生从以下三个小题中任选一个作答,若多选,则按所选的第一题计分.
A.(不等式选讲)若不等式的解集为,则的取值范围为_________.
B.(坐标系与参数方程)直线被曲线(为参数)所截得的弦长为_________.
C.(几何证明选讲)若直角的内切圆与斜边相切于点,且,则的面积为_________.
三、解答题(本大题共6小题,共75分)
16.(本题12分)在数列中,,且对任意的,都有.
(1)求证:数列是等差数列;
(2)设数列的前项和为,求证:对任意的,都为定值.
17.(本题12分)如图,已知四棱锥的底面是正方形,侧棱底面,,是的中点.
(1)证明平面;
(2)求二面角的余弦值.
18.(本题12分)在城的西南方向上有一个观测站,在城的南偏东的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城驶来.某一刻,在观测站处观测到汽车与处相距,在分钟后观测到汽车与处相距.若汽车速度为,求该汽车还需多长时间才能到达城
19.(本题12分)甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中三人答对的概率分别为,且各人回答得正确与否相互之间没有影响.
(1)若用表示甲队的总得分,求随机变量分布列和数学期望;
(2)用表示事件“甲、乙两队总得分之和为”,用表示事件“甲队总得分大于乙队总得分”,求.
20.(本题13分)已知直线的右焦点F,且交椭圆C于A,B两点.
(1)若抛物线的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对椭圆C,若直线L交y轴于点M,且,当m变化时,求的值.
21.(本题14分)
(1)讨论函数()的图像与直线的交点个数.
(2)求证:对任意的,不等式总成立.
陕西师大附中高2012届高考数学(理)答案
一、选择题(本大题共10题,每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B D B D A C A
二、填空题(本大题共5小题,每小题5分,共25分)
11.第四象限 12. 13.或 14. 15.A. B. C.
三、解答题(本大题共6小题,共75分)
16.(本题12分)在数列中,,且对任意的,都有.
(1)求证:数列是等差数列;
(2)设数列的前项和为,求证:对任意的,都为定值.
证明: (1)∵,∴.
∴数列是以为首项,为公差的等差数列.
(2) 由(1)知,∴.
∴.………………………………①
∴.……………………………………②
∴由②-①可得.
∴,故结论成立.
17.(本题12分)如图,已知四棱锥的底面是正方形,侧棱底面,,是的中点.
(1)证明平面;
(2)求二面角的余弦值.
解法一:(1)连结,设与交于点,连结.
∵底面ABCD是正方形,∴为的中点,又为的中点,
∴, ∵平面,平面,∴平面.
解法二:(1)以为坐标原点,分别以所在直线为轴建立空间直角坐标系,设,则.
∴,设是平面的一个法向量,
则由
∵,∴, ,∴
(2) 由(1)知是平面BDE的一个法向量,又是平面的一个法向量.设二面角的平面角为,由题意可知.
∴.
18.(本题12分)在城的西南方向上有一个观测站,在城的南偏东的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城驶来.某一刻,在观测站处观测到汽车与处相距,在分钟后观测到汽车与处相距.若汽车速度为,求该汽车还需多长时间才能到达城
解:如图,由题意知,.
则,从而.
故.
在△中,由正弦定理可得,
带入已知数据可求得,故.
所以,汽车要到达城还需要的时间为(分).
19.(本题12分)甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中三人答对的概率分别为,且各人回答得正确与否相互之间没有影响.
(1)若用表示甲队的总得分,求随机变量分布列和数学期望;
(2)用表示事件“甲、乙两队总得分之和为”,用表示事件“甲队总得分大于乙队总得分”,求.
解:(1)由题意知,的可能取值为,则有
,,
,.
所以的分布列为
故的数学期望
(2)用表示事件“甲队得分”,用表示事件“乙队得分”.因,且由于与为互斥事件,故.
∴.
20.(本题12分)已知直线的右焦点F,且交椭圆C于A,B两点.
(1)若抛物线的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对于(1)中的椭圆C,若直线L交y轴于点M,且,当m变化时,求的值.
解:(1)易知,,,. .
(2),设,则由可得:
,故. .
又由得.. 同理.
.
21.(本题14分)
(1)讨论函数()的图像与直线的交点个数.
(2)求证:对任意的,不等式总成立.
21.(1)解:由题意得:.令,得.
当时,,故函数在上递增;
当时,,故函数在上递减;
又因为,,,所以当或时,没有交点;当或时,有唯一的交点;当时,有两个交点.
(2)证明:由(1)知函数在上递增,在上递减,故在上的最大值为.即对均有,故.
当时,结论显然成立;当时,有:
.
综上可知,对任意的,不等式成立.
一、选择题(本大题共10题,每小题5分,共50分)
1.若集合,,且,则实数的取值范围为【 】.
A. B. C. D.
2.经问卷调查,某班学生对摄影分别持“喜欢”、“不喜欢”和“一般”三种态度,其中持“一般”态度的学生比持“不喜欢”的学生多人,按分层抽样的方法(抽样过程中不需要剔除个体)从全班选出部分学生进行关于摄影的座谈.若抽样得出的位同学中有位持“喜欢”态度的同学,位持“不喜欢”态度的同学和位持“一般”态度的同学,则全班持“喜欢”态度的同学人数为【 】.
A. B. C. D.
3.函数是【 】.
A.偶函数,在区间上单调递增 B.偶函数,在区间上单调递减
C.奇函数,在区间上单调递增 D.奇函数,在区间上单调递减
4.若圆锥的主视图(正视图)是一个边长为的等边三角形,则该圆锥的表面积为【 】.
A. B. C. D.
5.若数列是等差数列,则数列也为等差数列.类比这一性质可知,若正项数列是等比数列,且也是等比数列,则的表达式应为【 】.
A. B.
C. D.
6.若双曲线的一个焦点与抛物线的焦点相同,且双曲线的离心率为,则该双曲线的方程为【 】.
A. B. C. D.
7.按下面的流程图进行计算.若输出的,则输入的正实数值的个数最多为【 】.
A. B. C. D.
8.若三角函数的部分图象如下,则函数的解析式,以及的值分别为【 】.
A.,
B.,
C.,
D.,
9.在一次读书活动中,一同学从4本不同的科技书和2本不同的文艺书中任选3本,则所选的书中既有科技书又有文艺书的概率为【 】.
A. B. C. D.
10.已知实数满足,且.若为方程的两个实数根,则的取值范围为【 】.
A. B. C. D.
二、填空题(本大题共5小题,每小题5分,共25分)
11.若复数满足,则复数对应的点所在象限为 .
12.若向量,,,且,则 .
13.若函数,且,则的取值范围为________.
14.在直角坐标平面内,由不等式组所表示的平面区域的面积为_________.
15.请考生从以下三个小题中任选一个作答,若多选,则按所选的第一题计分.
A.(不等式选讲)若不等式的解集为,则的取值范围为_________.
B.(坐标系与参数方程)直线被曲线(为参数)所截得的弦长为_________.
C.(几何证明选讲)若直角的内切圆与斜边相切于点,且,则的面积为_________.
三、解答题(本大题共6小题,共75分)
16.(本题12分)在数列中,,且对任意的,都有.
(1)求证:数列是等差数列;
(2)设数列的前项和为,求证:对任意的,都为定值.
17.(本题12分)如图,已知四棱锥的底面是正方形,侧棱底面,,是的中点.
(1)证明平面;
(2)求二面角的余弦值.
18.(本题12分)在城的西南方向上有一个观测站,在城的南偏东的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城驶来.某一刻,在观测站处观测到汽车与处相距,在分钟后观测到汽车与处相距.若汽车速度为,求该汽车还需多长时间才能到达城
19.(本题12分)甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中三人答对的概率分别为,且各人回答得正确与否相互之间没有影响.
(1)若用表示甲队的总得分,求随机变量分布列和数学期望;
(2)用表示事件“甲、乙两队总得分之和为”,用表示事件“甲队总得分大于乙队总得分”,求.
20.(本题13分)已知直线的右焦点F,且交椭圆C于A,B两点.
(1)若抛物线的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对椭圆C,若直线L交y轴于点M,且,当m变化时,求的值.
21.(本题14分)
(1)讨论函数()的图像与直线的交点个数.
(2)求证:对任意的,不等式总成立.
陕西师大附中高2012届高考数学(理)答案
一、选择题(本大题共10题,每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B D B D A C A
二、填空题(本大题共5小题,每小题5分,共25分)
11.第四象限 12. 13.或 14. 15.A. B. C.
三、解答题(本大题共6小题,共75分)
16.(本题12分)在数列中,,且对任意的,都有.
(1)求证:数列是等差数列;
(2)设数列的前项和为,求证:对任意的,都为定值.
证明: (1)∵,∴.
∴数列是以为首项,为公差的等差数列.
(2) 由(1)知,∴.
∴.………………………………①
∴.……………………………………②
∴由②-①可得.
∴,故结论成立.
17.(本题12分)如图,已知四棱锥的底面是正方形,侧棱底面,,是的中点.
(1)证明平面;
(2)求二面角的余弦值.
解法一:(1)连结,设与交于点,连结.
∵底面ABCD是正方形,∴为的中点,又为的中点,
∴, ∵平面,平面,∴平面.
解法二:(1)以为坐标原点,分别以所在直线为轴建立空间直角坐标系,设,则.
∴,设是平面的一个法向量,
则由
∵,∴, ,∴
(2) 由(1)知是平面BDE的一个法向量,又是平面的一个法向量.设二面角的平面角为,由题意可知.
∴.
18.(本题12分)在城的西南方向上有一个观测站,在城的南偏东的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城驶来.某一刻,在观测站处观测到汽车与处相距,在分钟后观测到汽车与处相距.若汽车速度为,求该汽车还需多长时间才能到达城
解:如图,由题意知,.
则,从而.
故.
在△中,由正弦定理可得,
带入已知数据可求得,故.
所以,汽车要到达城还需要的时间为(分).
19.(本题12分)甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中三人答对的概率分别为,且各人回答得正确与否相互之间没有影响.
(1)若用表示甲队的总得分,求随机变量分布列和数学期望;
(2)用表示事件“甲、乙两队总得分之和为”,用表示事件“甲队总得分大于乙队总得分”,求.
解:(1)由题意知,的可能取值为,则有
,,
,.
所以的分布列为
故的数学期望
(2)用表示事件“甲队得分”,用表示事件“乙队得分”.因,且由于与为互斥事件,故.
∴.
20.(本题12分)已知直线的右焦点F,且交椭圆C于A,B两点.
(1)若抛物线的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对于(1)中的椭圆C,若直线L交y轴于点M,且,当m变化时,求的值.
解:(1)易知,,,. .
(2),设,则由可得:
,故. .
又由得.. 同理.
.
21.(本题14分)
(1)讨论函数()的图像与直线的交点个数.
(2)求证:对任意的,不等式总成立.
21.(1)解:由题意得:.令,得.
当时,,故函数在上递增;
当时,,故函数在上递减;
又因为,,,所以当或时,没有交点;当或时,有唯一的交点;当时,有两个交点.
(2)证明:由(1)知函数在上递增,在上递减,故在上的最大值为.即对均有,故.
当时,结论显然成立;当时,有:
.
综上可知,对任意的,不等式成立.
同课章节目录
