六年级数学下册课件 鸽巢问题 人教版(共32张PPT)
文档属性
| 名称 | 六年级数学下册课件 鸽巢问题 人教版(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 09:42:40 | ||
图片预览




文档简介
(共26张PPT)
鸽巢问题 例1 例2
鸽巢问题
一、游戏引入
我给大家表演一个“魔术”。一副牌,取出大小王,还剩52张,你们5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?
(一)例1
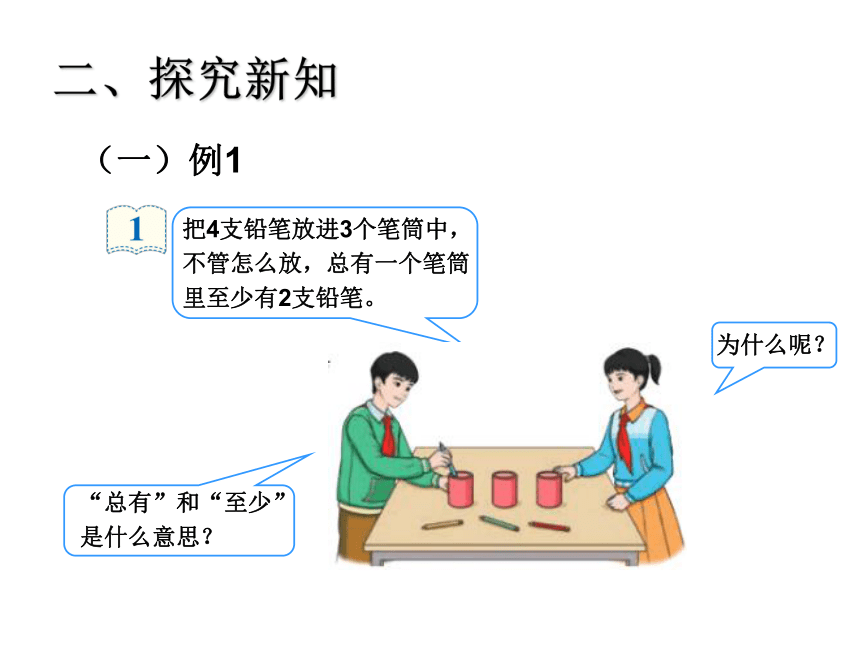
二、探究新知
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
为什么呢?
“总有”和“至少”是什么意思?
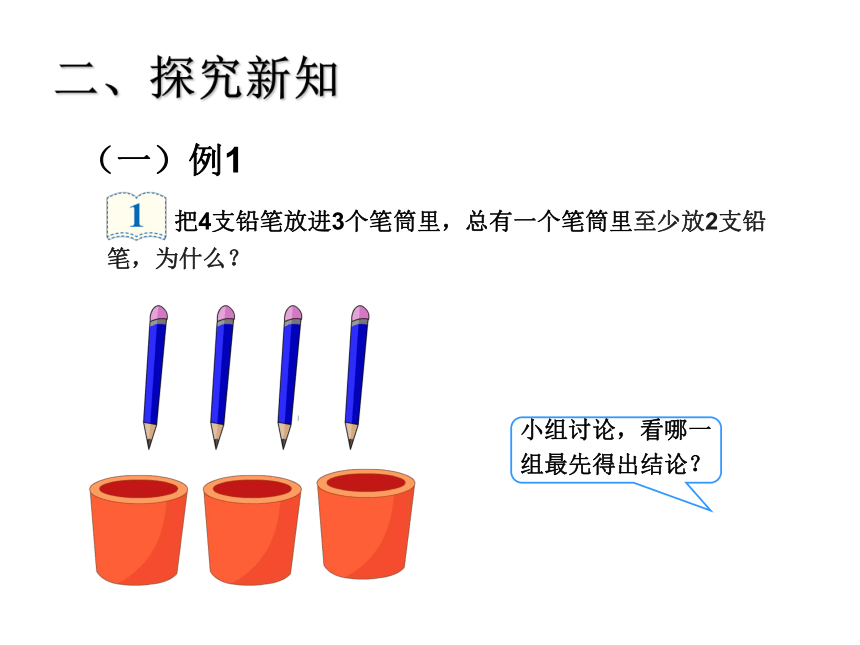
把4支铅笔放进3个笔筒里,总有一个笔筒里至少放2支铅笔,为什么?
二、探究新知
(一)例1
小组讨论,看哪一组最先得出结论?
二、探究新知
(一)例1
我把各种情况都摆出来了。
还可以这样想:先放3支,在每个笔筒中放1支,剩下的1支就要放进其中的一个笔筒。所以至少有一个笔筒中有2支铅笔。
二、探究新知
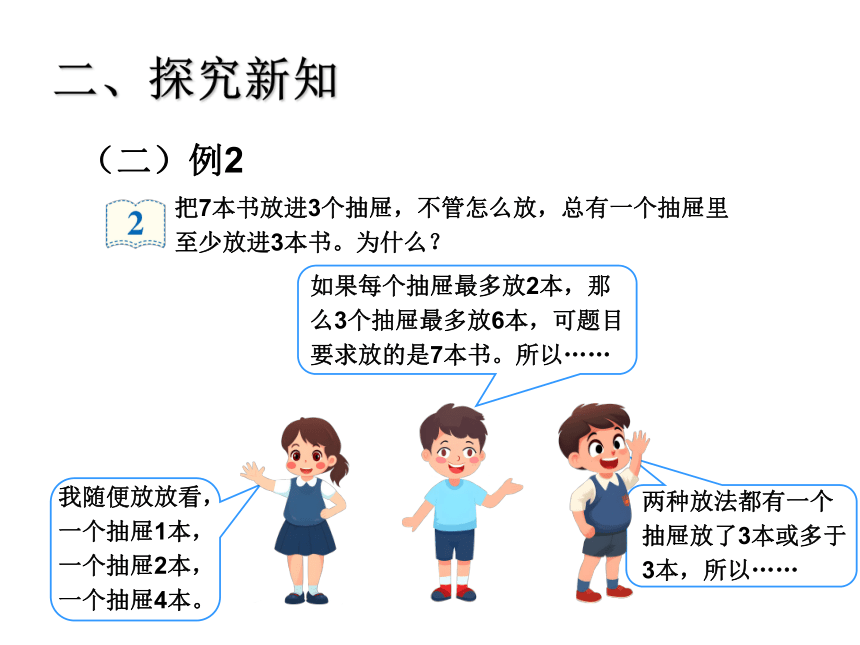
把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
(二)例2
我随便放放看,
一个抽屉1本,
一个抽屉2本,
一个抽屉4本。
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以……
两种放法都有一个抽屉放了3本或多于3本,所以……
二、探究新知
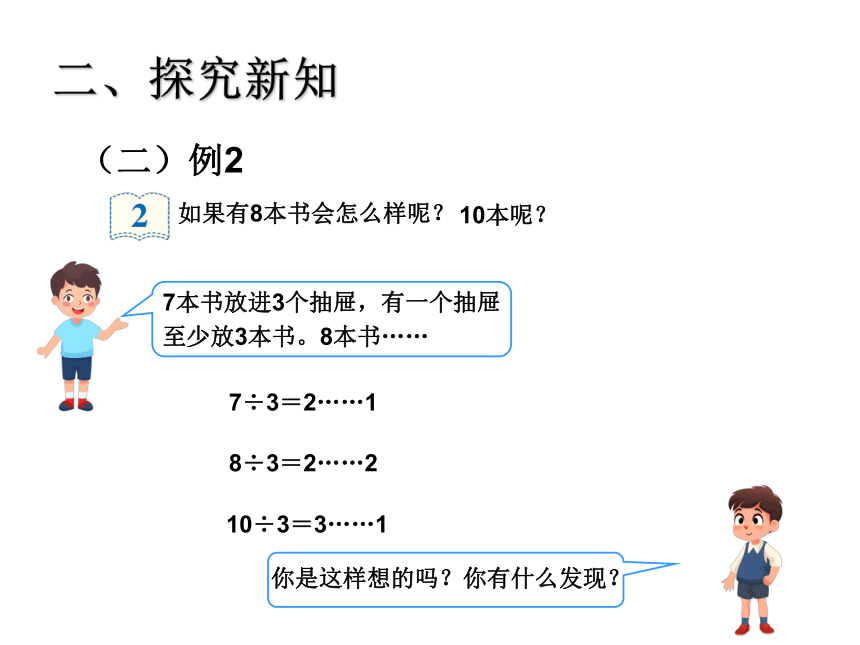
如果有8本书会怎么样呢?
10本呢?
7÷3=2……1
8÷3=2……2
10÷3=3……1
(二)例2
7本书放进3个抽屉,有一个抽屉至少放3本书。8本书……
你是这样想的吗?你有什么发现?
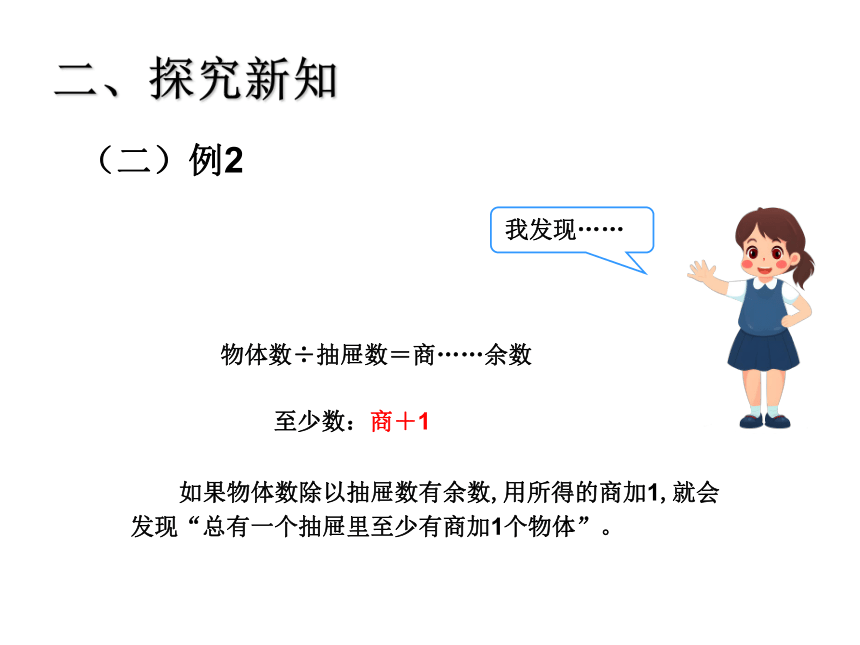
物体数÷抽屉数=商……余数
至少数:商+1
如果物体数除以抽屉数有余数,用所得的商加1,就会发现“总有一个抽屉里至少有商加1个物体”。
二、探究新知
(二)例2
我发现……
1. 5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只
鸽子。为什么?
5÷3=1……2
1+1=2
三、知识应用
(一)做一做
2. 11只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了3只
鸽子。为什么?
11÷4=2……3
2+1=3
三、知识应用
(一)做一做
3. 5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1……1
1+1=2
三、知识应用
(一)做一做
想一想,商1和余数1各表示什么?
随意找13位老师,他们中至少有2个人的属相相同。为什么?
13÷12=1……1
1+1=2
三、知识应用
(二)解决问题
为什么要用1+1呢?
四、布置作业
作业:第71页练习十三,第2题、第3题。
鸽巢问题 例3
鸽巢问题
摸出5个球,肯定有2个同色的,因为……
一、探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
只摸2个球能保证是同色的吗?
有两种颜色。那摸3个球就能保证……
一、探究新知
第一种情况:
第二种情况:
第三种情况:
验证:球的颜色共有2种,如果只摸出2个球,会出现三种情况:1个红球和1个蓝球、2个红球、2个蓝球。因此,如果摸出的2个球正好是一红一蓝时就不能满足条件。
猜测1:只摸2个球就能保证是同色的。
一、探究新知
第三种情况:
第四种情况:
验证:把红、蓝两种颜色看成2个“鸽巢”,因为5÷2=2……1,所以摸出5个球时,至少有3个球是同色的,显然,摸出5个球不是最少的。
猜测2:摸出5个球,肯定有2个是同色的。
第一种情况:
第二种情况:
一、探究新知
第一种情况:
第二种情况:
猜测3:有两种颜色。那摸3个球就能保证有2个同色的球。
一、探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为……
只摸2个球能保证是同色的吗?
有两种颜色。那摸3个球就能保证……
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
(一)做一做
1. 向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
367÷365=1……2
1+1=2
49÷12=4……1
4+1=5
二、知识应用
六年级里至少有两人的生日是同一天。
六(2)班中至少有5人是同一个月出生的。
(一)做一做
2. 把红、黄、蓝、白四种颜色的球各10个放到一个袋子
里。至少取多少个球,可以保证取到两个颜色相同的球?
我们从最不利的原则
去考虑:
假设我们每种颜色的都拿一个,需要拿4个,但是没有同色的,要想有同色的需要再拿1个球,不论是哪一种颜色的,都一定有2个同色的。
4+1=5
二、知识应用
(二)解决问题
1. 希望小学篮球兴趣小组的同学中,最大的12岁,最小的6岁,
最少从中挑选几名学生,就一定能找到两个学生年龄相同。
7+1=8
二、知识应用
从6岁到12岁有几个年龄段?
(二)解决问题
2. 从一副扑克牌(52张,没有大小王)中要抽出几张牌来,
才能保证有一张是红桃?54张呢?
13×3+1=40
二、知识应用
最后为什么要加1?
2+13×3+1=42
13
13
13
13
三、知识拓展
德国 数学家
狄里克雷(1805.2.13.~1859.5.5.)
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
四、布置作业
作业:第71页练习十三,第4题、
第5题、第6题。
鸽巢问题 例1 例2
鸽巢问题
一、游戏引入
我给大家表演一个“魔术”。一副牌,取出大小王,还剩52张,你们5人每人随意抽一张,我知道至少有2张牌是同花色的。相信吗?
(一)例1
二、探究新知
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
为什么呢?
“总有”和“至少”是什么意思?
把4支铅笔放进3个笔筒里,总有一个笔筒里至少放2支铅笔,为什么?
二、探究新知
(一)例1
小组讨论,看哪一组最先得出结论?
二、探究新知
(一)例1
我把各种情况都摆出来了。
还可以这样想:先放3支,在每个笔筒中放1支,剩下的1支就要放进其中的一个笔筒。所以至少有一个笔筒中有2支铅笔。
二、探究新知
把7本书放进3个抽屉,不管怎么放,总有一个抽屉里至少放进3本书。为什么?
(二)例2
我随便放放看,
一个抽屉1本,
一个抽屉2本,
一个抽屉4本。
如果每个抽屉最多放2本,那么3个抽屉最多放6本,可题目要求放的是7本书。所以……
两种放法都有一个抽屉放了3本或多于3本,所以……
二、探究新知
如果有8本书会怎么样呢?
10本呢?
7÷3=2……1
8÷3=2……2
10÷3=3……1
(二)例2
7本书放进3个抽屉,有一个抽屉至少放3本书。8本书……
你是这样想的吗?你有什么发现?
物体数÷抽屉数=商……余数
至少数:商+1
如果物体数除以抽屉数有余数,用所得的商加1,就会发现“总有一个抽屉里至少有商加1个物体”。
二、探究新知
(二)例2
我发现……
1. 5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只
鸽子。为什么?
5÷3=1……2
1+1=2
三、知识应用
(一)做一做
2. 11只鸽子飞进了4个鸽笼,总有一个鸽笼至少飞进了3只
鸽子。为什么?
11÷4=2……3
2+1=3
三、知识应用
(一)做一做
3. 5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1……1
1+1=2
三、知识应用
(一)做一做
想一想,商1和余数1各表示什么?
随意找13位老师,他们中至少有2个人的属相相同。为什么?
13÷12=1……1
1+1=2
三、知识应用
(二)解决问题
为什么要用1+1呢?
四、布置作业
作业:第71页练习十三,第2题、第3题。
鸽巢问题 例3
鸽巢问题
摸出5个球,肯定有2个同色的,因为……
一、探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
只摸2个球能保证是同色的吗?
有两种颜色。那摸3个球就能保证……
一、探究新知
第一种情况:
第二种情况:
第三种情况:
验证:球的颜色共有2种,如果只摸出2个球,会出现三种情况:1个红球和1个蓝球、2个红球、2个蓝球。因此,如果摸出的2个球正好是一红一蓝时就不能满足条件。
猜测1:只摸2个球就能保证是同色的。
一、探究新知
第三种情况:
第四种情况:
验证:把红、蓝两种颜色看成2个“鸽巢”,因为5÷2=2……1,所以摸出5个球时,至少有3个球是同色的,显然,摸出5个球不是最少的。
猜测2:摸出5个球,肯定有2个是同色的。
第一种情况:
第二种情况:
一、探究新知
第一种情况:
第二种情况:
猜测3:有两种颜色。那摸3个球就能保证有2个同色的球。
一、探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球?
摸出5个球,肯定有2个同色的,因为……
只摸2个球能保证是同色的吗?
有两种颜色。那摸3个球就能保证……
只要摸出的球数比它们的颜色种数多1,就能保证有两个球同色。
(一)做一做
1. 向东小学六年级共有367名学生,其中六(2)班有49名学生。
他们说得对吗?为什么?
367÷365=1……2
1+1=2
49÷12=4……1
4+1=5
二、知识应用
六年级里至少有两人的生日是同一天。
六(2)班中至少有5人是同一个月出生的。
(一)做一做
2. 把红、黄、蓝、白四种颜色的球各10个放到一个袋子
里。至少取多少个球,可以保证取到两个颜色相同的球?
我们从最不利的原则
去考虑:
假设我们每种颜色的都拿一个,需要拿4个,但是没有同色的,要想有同色的需要再拿1个球,不论是哪一种颜色的,都一定有2个同色的。
4+1=5
二、知识应用
(二)解决问题
1. 希望小学篮球兴趣小组的同学中,最大的12岁,最小的6岁,
最少从中挑选几名学生,就一定能找到两个学生年龄相同。
7+1=8
二、知识应用
从6岁到12岁有几个年龄段?
(二)解决问题
2. 从一副扑克牌(52张,没有大小王)中要抽出几张牌来,
才能保证有一张是红桃?54张呢?
13×3+1=40
二、知识应用
最后为什么要加1?
2+13×3+1=42
13
13
13
13
三、知识拓展
德国 数学家
狄里克雷(1805.2.13.~1859.5.5.)
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
四、布置作业
作业:第71页练习十三,第4题、
第5题、第6题。
