苏科版九年级上册数学教案 2.7 弧长及扇形的面积
文档属性
| 名称 | 苏科版九年级上册数学教案 2.7 弧长及扇形的面积 |

|
|
| 格式 | zip | ||
| 文件大小 | 417.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览

文档简介
2.7
弧长及扇形的面积
教学目标:
1、经历探索弧长计算公式及扇形面积计算公式的过程;
2、了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题。
教学重点、难点:
重点:弧长与扇形的计算公式的推导与应用
难点:弧长与扇形的计算公式的应用
教学过程:
一、情境创设
创设情境:制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,
试计算图所示管道的展直长度L(单位:mm,精确到1mm)
二、探索活动
活动一探索弧长计算公式
(1)半径为R的圆,周长是_______
(2)圆的周长可以看作是_____度的圆心角
所对的弧
(3)1°圆心角所对的弧长是圆周长的_____
1°圆心角所对弧长是__________
(4)n°圆心角所对的弧长是1°圆心角所对的弧长的______倍,
(5)n°圆心角所对弧长是__________
注:引导学生用“方程的观点”去认识弧长计算公式,它揭示了l、n、R这3个量之间的一种相等关系。如果这三个量中,任意知道两个量,就可以根据公式求出第三个量。
牛刀小试:(1)已知圆的半径为10cm,半圆的弧长为_______
(2)已知圆的半径为9cm
,60°圆心角所对的弧长为______
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______
(4)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______
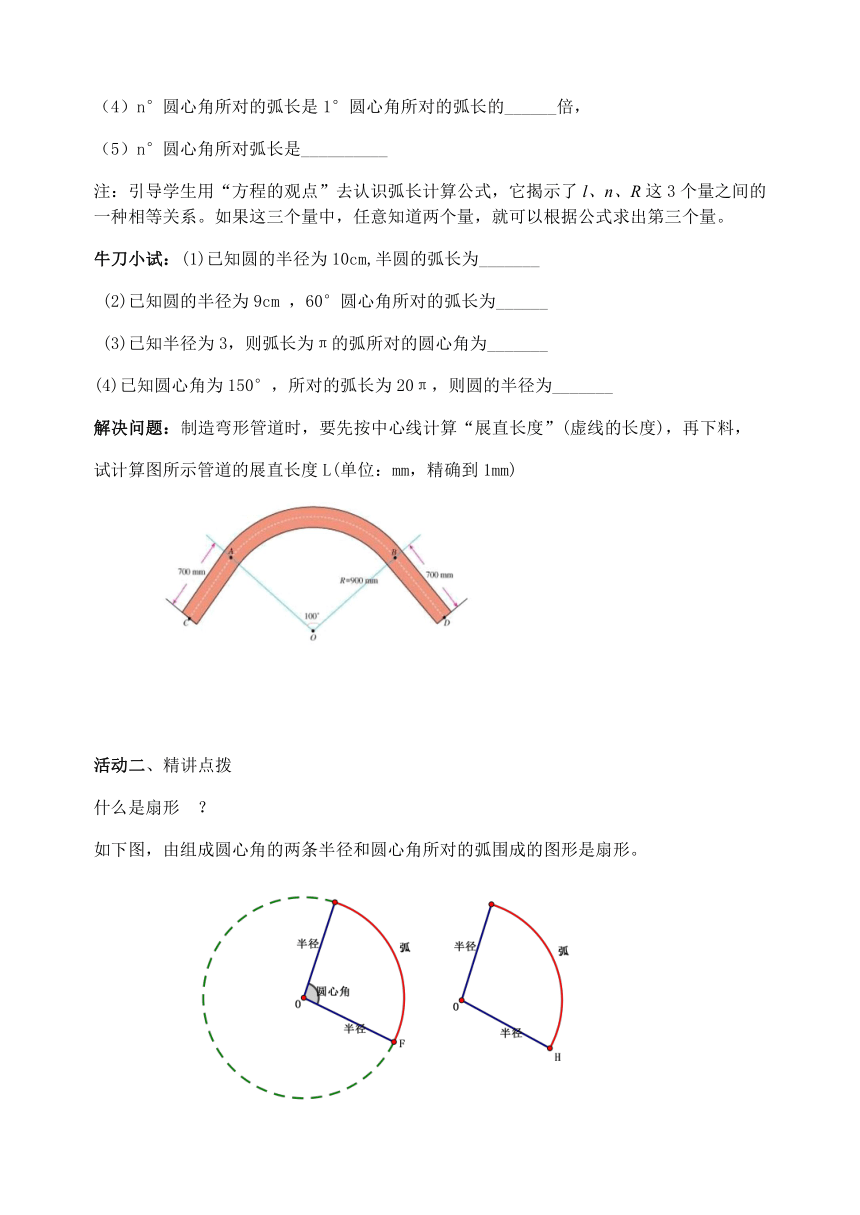
解决问题:制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,
试计算图所示管道的展直长度L(单位:mm,精确到1mm)
活动二、精讲点拨
什么是扇形
?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
探索扇形面积计算公式
(1)半径为R的圆,面积是__________
(2)圆的面积可以看作是______度的圆心角所对的扇形
圆心角为1°的扇形的面积是圆的面积的_____
圆心角为1°的扇形的面积是______
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积的______倍,
(4)圆心角为n°的扇形的面积是_____
注:类似于弧长的计算公式,扇形面积的计算公式也是表示三个量之间的相等关系,在S、n、R中任意知道两个量都可以根据公式求出第三个量的值。
2、扇形面积的另一个计算公式
比较扇形面积计算公式与弧长计算公式,可以发现:可以将扇形面积的计算公式:
S=πR2化为S=_______·R=_______·R,从面可得扇形面积的另一计算公式:
S扇=_______。
小试牛刀
4.已知一扇形的半径为6cm,其弧长为(7/4)πcm,
则这个扇形的面积=
______
5.已知一扇形的半径为5cm,其面积为(5/3)πcm,则这个扇形的弧长=
_______
6.一个弧长与面积都是
(9/5)π的扇形,
它的半径R=
________
体会分享:通过本节课的学习,我知道了……学到了……感受到了……
拓展延伸:⊙A,
⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少?
变式:
正三角形ABC的边长为a,分别以A、B、C为圆心,为半径的圆两两相切于点O1、O2、O3。求弧O1O2、弧O2O3、弧O3O1围成的图形面积S(图中阴影部分)。
课堂作业
弧长及扇形的面积
教学目标:
1、经历探索弧长计算公式及扇形面积计算公式的过程;
2、了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题。
教学重点、难点:
重点:弧长与扇形的计算公式的推导与应用
难点:弧长与扇形的计算公式的应用
教学过程:
一、情境创设
创设情境:制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,
试计算图所示管道的展直长度L(单位:mm,精确到1mm)
二、探索活动
活动一探索弧长计算公式
(1)半径为R的圆,周长是_______
(2)圆的周长可以看作是_____度的圆心角
所对的弧
(3)1°圆心角所对的弧长是圆周长的_____
1°圆心角所对弧长是__________
(4)n°圆心角所对的弧长是1°圆心角所对的弧长的______倍,
(5)n°圆心角所对弧长是__________
注:引导学生用“方程的观点”去认识弧长计算公式,它揭示了l、n、R这3个量之间的一种相等关系。如果这三个量中,任意知道两个量,就可以根据公式求出第三个量。
牛刀小试:(1)已知圆的半径为10cm,半圆的弧长为_______
(2)已知圆的半径为9cm
,60°圆心角所对的弧长为______
(3)已知半径为3,则弧长为π的弧所对的圆心角为_______
(4)已知圆心角为150°,所对的弧长为20π,则圆的半径为_______
解决问题:制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,
试计算图所示管道的展直长度L(单位:mm,精确到1mm)
活动二、精讲点拨
什么是扇形
?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
探索扇形面积计算公式
(1)半径为R的圆,面积是__________
(2)圆的面积可以看作是______度的圆心角所对的扇形
圆心角为1°的扇形的面积是圆的面积的_____
圆心角为1°的扇形的面积是______
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积的______倍,
(4)圆心角为n°的扇形的面积是_____
注:类似于弧长的计算公式,扇形面积的计算公式也是表示三个量之间的相等关系,在S、n、R中任意知道两个量都可以根据公式求出第三个量的值。
2、扇形面积的另一个计算公式
比较扇形面积计算公式与弧长计算公式,可以发现:可以将扇形面积的计算公式:
S=πR2化为S=_______·R=_______·R,从面可得扇形面积的另一计算公式:
S扇=_______。
小试牛刀
4.已知一扇形的半径为6cm,其弧长为(7/4)πcm,
则这个扇形的面积=
______
5.已知一扇形的半径为5cm,其面积为(5/3)πcm,则这个扇形的弧长=
_______
6.一个弧长与面积都是
(9/5)π的扇形,
它的半径R=
________
体会分享:通过本节课的学习,我知道了……学到了……感受到了……
拓展延伸:⊙A,
⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形的面积之和为多少?弧长的和为多少?
变式:
正三角形ABC的边长为a,分别以A、B、C为圆心,为半径的圆两两相切于点O1、O2、O3。求弧O1O2、弧O2O3、弧O3O1围成的图形面积S(图中阴影部分)。
课堂作业
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
