苏科版九年级上册数学教案 2.8圆锥的侧面积
文档属性
| 名称 | 苏科版九年级上册数学教案 2.8圆锥的侧面积 |
|
|
| 格式 | zip | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览



文档简介
2.8圆锥的侧面积以及全面积
知识梳理
扇形、圆柱和圆锥的相关计算公式
1、扇形:(1)弧长公式:;
(2)扇形面积公式:
:圆心角
:扇形多对应的圆的半径
:扇形弧长
:扇形面积
2、圆柱:
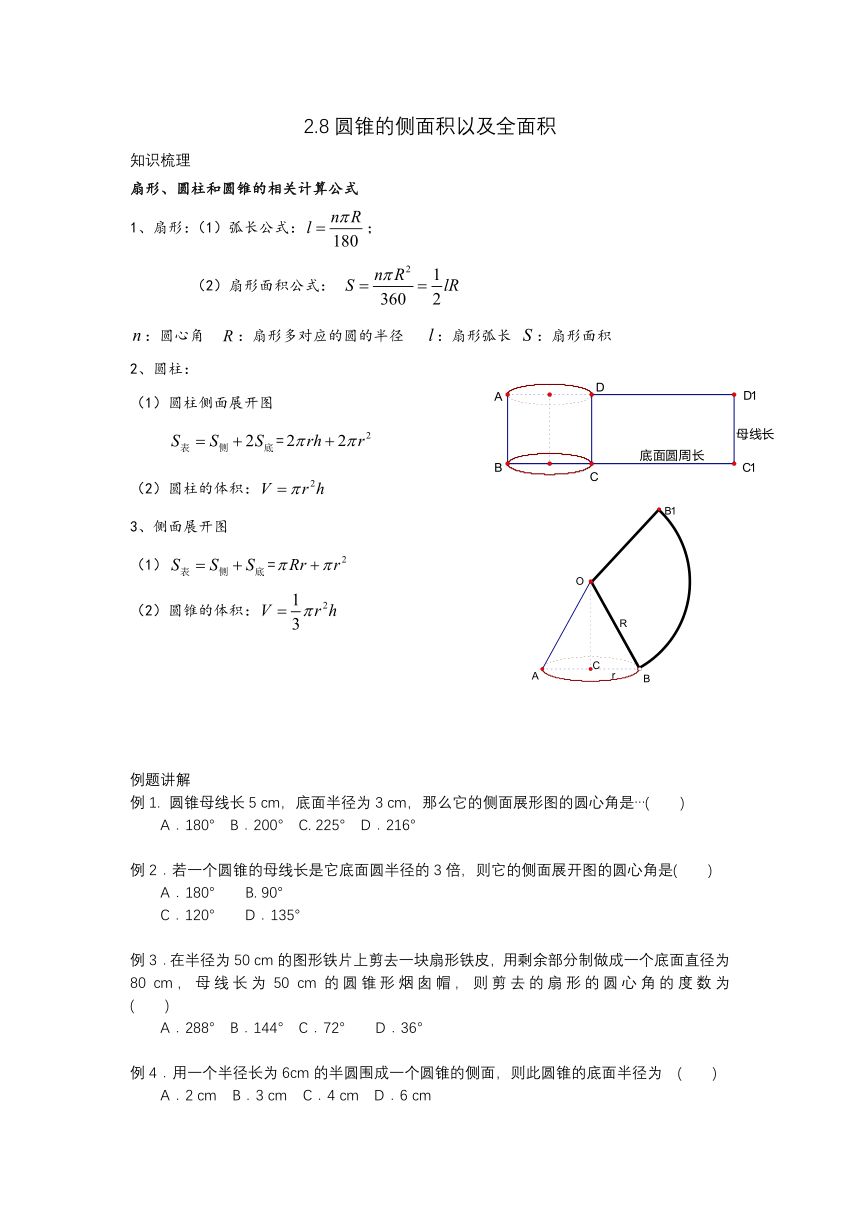
(1)圆柱侧面展开图
=
(2)圆柱的体积:
3、侧面展开图
(1)=
(2)圆锥的体积:
例题讲解
例1.
圆锥母线长5
cm,底面半径为3
cm,那么它的侧面展形图的圆心角是…(
)
A.180°
B.200°
C.
225°
D.216°
例2.若一个圆锥的母线长是它底面圆半径的3倍,则它的侧面展开图的圆心角是(
)
A.180°
B.
90°
C.120°
D.135°
例3.在半径为50
cm的图形铁片上剪去一块扇形铁皮,用剩余部分制做成一个底面直径为80
cm,母线长为50
cm的圆锥形烟囱帽,则剪去的扇形的圆心角的度数为
(
)
A.288°
B.144°
C.72°
D.36°
例4.用一个半径长为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面半径为
(
)
A.2
cm
B.3
cm
C.4
cm
D.6
cm
例5.已知一个扇形的半径为60厘米,圆心角为150°,若用它做成一个圆锥的侧面,则这个圆锥的底面半径为(
)
(A)12.5厘米(B)25厘米(C)50厘米(D)75厘米
例6.一个圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角是(
)
(A)60°
(B)90°
(C)120°(D)180°
例7.若圆锥的底面半径是3cm,母线长是5cm,则它的侧面展开图的面积是_______
例8.若圆锥的母线长为5cm,高为3cm,则其侧面展开图中扇形的圆心角是
度.
例9.已知扇形的圆心角为120°,面积为300πcm2
。(1)扇形的弧长=
;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是
例10.圆锥的母线为13cm,侧面展开图的面积为65πcm2,则这个圆锥的高为
.
例11.△BAC中,AB=5,AC=12,BC=13,以AC所在的直线为轴将△ABC旋转一周得一个几何体,这个几何体的表面积是多少?
巩固练习
1.某抗震篷的顶部是圆锥形,这个圆锥的底面直径为10
m,母线长为6
m,为了防晒,需要在它的顶部铺上油毡,所需油毡的面积至少是
(
)
A.30
m2
B.60
m2
C.30
m2
D.60
m2
2.一个圆锥的侧面展开图形是半径为8
cm、圆心角为1200的扇形,则此圆锥的底面半径为
(
)
A.cm
B.cm
C.3
cm
D.cm
3.一个圆锥的母线长为6,高为,则它的底面圆的半径为________,侧面积为________,全面积为________,它的侧面展开图的圆心角等于________.
4.已知圆锥的底面半径等于它的高的一半,若侧面积是cm2
,则它的底面半径是________cm.
5.如图,扇形OAB的圆心角为120o,半径为6
cm若将此扇形围成一个圆锥的侧面(不计接缝),求这个圆锥的底面半径.
6.已知扇形的圆心角为120o,面积为300cm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面的面积是多少?
7.如图,一个机器零件,它的上半部分是一个圆锥,下半部分是一个圆柱,按图中标出的尺寸(单位:cm),计算它的表面积.(精确到1
cm2)
8.将半径为1
m、圆心角为90o的扇形薄铁板围成一个圆锥筒,在计算圆锥的容积(接缝忽略不计)时,李明认为圆锥的高就等于扇形的圆心O到弦AB的距离(OC的长(如图),马强说这样计算不正确,你同意谁的说法?请把你认为正确的计算过程写出来.
9.如图,一个圆锥的母线长为20
cm,底面半径为5
cm.在圆锥下底面的点A处有一只蚂蚁,想吃到与点A相对的母线的中点B处的一粒粘住的砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线是多长?(精确到0.1
cm)
10.扇形的圆心角为1200,面积为300
cm2.
(1)求扇形的弧长.
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是多少?
11.如图,小明从半径为5
cm的圆形纸片中剪下40%圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为
(
).
A.3
cm
B.4
cm
C.
cm、
D.
cm
12.如图,这是一个由圆柱形材料加工而成的零件,它是在网柱体的内部“掏去”一个以圆柱体的上底面为底面、与圆柱体等高的圆锥而得到的.已知圆柱的底面直径AB=12
cm.高BC=8
cm求这个零件的表面积.(结果保留)
13.如图,一个空间几何体的主视图左视图都是边长为1的正三角形.俯视图是一个圆,那么这个几何体的侧面积是_________.
14.已知O为圆锥的顶点,M为圆锥底面一点,点P在OM上。一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如右图示.若沿OM将圆锥侧向剪开并展开,所得侧面展开是
(
).
15.
李老师在与同学们进行“蚂蚁怎样爬最近’’的课题研究时设计了以下三个问题,请你根据所给的条件分别求出蚂蚁需要爬行的最短路程.
(1)如图①,正方体的棱长为5
cm,一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C、处.
(2)如图②,正四棱柱的底面边长为5
cm,侧棱长为6
cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C、处.
(3)如图③,圆锥的母线长为4
cm,圆锥的侧面展开图如图④所示,且AOA’=1200,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A。
巩固练习答案
1.C
2.A
3.1
6
7
60o
4.
5.扇形弧长为4.
圆锥的底面半径为2
cm.
6.(1)扇形的弧长为20cm.
(2)圆锥的轴截面的面积是cm2.
7.
AB=
13.
圆柱的侧面积为200
(cm2).
圆柱的底面积为25
(cm2).
圆锥的侧面积为65(cm2).
全面积约为911(cm2).
8.提示:设围成圆锥的底面圆的圆心为O',易
知OC=,
OO'=.所以李明的说法不正确.
9.14.7
cm
10(1)扇形的半径为R
cm,弧长为l
cm,则.
解得R=30,即扇形的半径为30cm.
×30l=300,解得l=20.
即扇形的弧长为20cm
(2)设此扇形卷成一个圆锥后,底面圆的半径为r
cm,则2r=20,r=10.
圆锥的高为
=20
(cm),
这个圆锥的轴截面面积是×2r×h=200
(cm2)
11.C
12.这个零件的底面积为36(cm2).
这个零件的外侧面积为96(cm2).
圆锥的母线长为10(cm).
这个零件的内侧面积为60(cm2).
所以这个零件的表面积为36+96+60=192(cm2).
13.
14.D
15.
.(1)AC’=(cm)
(2)分两种情况:①AC’=;
②AC’=.>,最短路程为
cm
(3)由已知得所求的最短的路程为AA’=4cm
知识梳理
扇形、圆柱和圆锥的相关计算公式
1、扇形:(1)弧长公式:;
(2)扇形面积公式:
:圆心角
:扇形多对应的圆的半径
:扇形弧长
:扇形面积
2、圆柱:
(1)圆柱侧面展开图
=
(2)圆柱的体积:
3、侧面展开图
(1)=
(2)圆锥的体积:
例题讲解
例1.
圆锥母线长5
cm,底面半径为3
cm,那么它的侧面展形图的圆心角是…(
)
A.180°
B.200°
C.
225°
D.216°
例2.若一个圆锥的母线长是它底面圆半径的3倍,则它的侧面展开图的圆心角是(
)
A.180°
B.
90°
C.120°
D.135°
例3.在半径为50
cm的图形铁片上剪去一块扇形铁皮,用剩余部分制做成一个底面直径为80
cm,母线长为50
cm的圆锥形烟囱帽,则剪去的扇形的圆心角的度数为
(
)
A.288°
B.144°
C.72°
D.36°
例4.用一个半径长为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面半径为
(
)
A.2
cm
B.3
cm
C.4
cm
D.6
cm
例5.已知一个扇形的半径为60厘米,圆心角为150°,若用它做成一个圆锥的侧面,则这个圆锥的底面半径为(
)
(A)12.5厘米(B)25厘米(C)50厘米(D)75厘米
例6.一个圆锥的侧面积是底面积的2倍,这个圆锥的侧面展开图扇形的圆心角是(
)
(A)60°
(B)90°
(C)120°(D)180°
例7.若圆锥的底面半径是3cm,母线长是5cm,则它的侧面展开图的面积是_______
例8.若圆锥的母线长为5cm,高为3cm,则其侧面展开图中扇形的圆心角是
度.
例9.已知扇形的圆心角为120°,面积为300πcm2
。(1)扇形的弧长=
;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是
例10.圆锥的母线为13cm,侧面展开图的面积为65πcm2,则这个圆锥的高为
.
例11.△BAC中,AB=5,AC=12,BC=13,以AC所在的直线为轴将△ABC旋转一周得一个几何体,这个几何体的表面积是多少?
巩固练习
1.某抗震篷的顶部是圆锥形,这个圆锥的底面直径为10
m,母线长为6
m,为了防晒,需要在它的顶部铺上油毡,所需油毡的面积至少是
(
)
A.30
m2
B.60
m2
C.30
m2
D.60
m2
2.一个圆锥的侧面展开图形是半径为8
cm、圆心角为1200的扇形,则此圆锥的底面半径为
(
)
A.cm
B.cm
C.3
cm
D.cm
3.一个圆锥的母线长为6,高为,则它的底面圆的半径为________,侧面积为________,全面积为________,它的侧面展开图的圆心角等于________.
4.已知圆锥的底面半径等于它的高的一半,若侧面积是cm2
,则它的底面半径是________cm.
5.如图,扇形OAB的圆心角为120o,半径为6
cm若将此扇形围成一个圆锥的侧面(不计接缝),求这个圆锥的底面半径.
6.已知扇形的圆心角为120o,面积为300cm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面的面积是多少?
7.如图,一个机器零件,它的上半部分是一个圆锥,下半部分是一个圆柱,按图中标出的尺寸(单位:cm),计算它的表面积.(精确到1
cm2)
8.将半径为1
m、圆心角为90o的扇形薄铁板围成一个圆锥筒,在计算圆锥的容积(接缝忽略不计)时,李明认为圆锥的高就等于扇形的圆心O到弦AB的距离(OC的长(如图),马强说这样计算不正确,你同意谁的说法?请把你认为正确的计算过程写出来.
9.如图,一个圆锥的母线长为20
cm,底面半径为5
cm.在圆锥下底面的点A处有一只蚂蚁,想吃到与点A相对的母线的中点B处的一粒粘住的砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线是多长?(精确到0.1
cm)
10.扇形的圆心角为1200,面积为300
cm2.
(1)求扇形的弧长.
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是多少?
11.如图,小明从半径为5
cm的圆形纸片中剪下40%圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为
(
).
A.3
cm
B.4
cm
C.
cm、
D.
cm
12.如图,这是一个由圆柱形材料加工而成的零件,它是在网柱体的内部“掏去”一个以圆柱体的上底面为底面、与圆柱体等高的圆锥而得到的.已知圆柱的底面直径AB=12
cm.高BC=8
cm求这个零件的表面积.(结果保留)
13.如图,一个空间几何体的主视图左视图都是边长为1的正三角形.俯视图是一个圆,那么这个几何体的侧面积是_________.
14.已知O为圆锥的顶点,M为圆锥底面一点,点P在OM上。一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如右图示.若沿OM将圆锥侧向剪开并展开,所得侧面展开是
(
).
15.
李老师在与同学们进行“蚂蚁怎样爬最近’’的课题研究时设计了以下三个问题,请你根据所给的条件分别求出蚂蚁需要爬行的最短路程.
(1)如图①,正方体的棱长为5
cm,一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C、处.
(2)如图②,正四棱柱的底面边长为5
cm,侧棱长为6
cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C、处.
(3)如图③,圆锥的母线长为4
cm,圆锥的侧面展开图如图④所示,且AOA’=1200,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A。
巩固练习答案
1.C
2.A
3.1
6
7
60o
4.
5.扇形弧长为4.
圆锥的底面半径为2
cm.
6.(1)扇形的弧长为20cm.
(2)圆锥的轴截面的面积是cm2.
7.
AB=
13.
圆柱的侧面积为200
(cm2).
圆柱的底面积为25
(cm2).
圆锥的侧面积为65(cm2).
全面积约为911(cm2).
8.提示:设围成圆锥的底面圆的圆心为O',易
知OC=,
OO'=.所以李明的说法不正确.
9.14.7
cm
10(1)扇形的半径为R
cm,弧长为l
cm,则.
解得R=30,即扇形的半径为30cm.
×30l=300,解得l=20.
即扇形的弧长为20cm
(2)设此扇形卷成一个圆锥后,底面圆的半径为r
cm,则2r=20,r=10.
圆锥的高为
=20
(cm),
这个圆锥的轴截面面积是×2r×h=200
(cm2)
11.C
12.这个零件的底面积为36(cm2).
这个零件的外侧面积为96(cm2).
圆锥的母线长为10(cm).
这个零件的内侧面积为60(cm2).
所以这个零件的表面积为36+96+60=192(cm2).
13.
14.D
15.
.(1)AC’=(cm)
(2)分两种情况:①AC’=;
②AC’=.>,最短路程为
cm
(3)由已知得所求的最短的路程为AA’=4cm
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
