第19章矩形、菱形与正方形单元基础练-2020-2021学年华东师大版数学八年级下册(Word版含答案)
文档属性
| 名称 | 第19章矩形、菱形与正方形单元基础练-2020-2021学年华东师大版数学八年级下册(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 00:00:00 | ||
图片预览

文档简介
八年级第二学期数学第19章矩形、菱形与正方形单元基础练-2020-2021学年华东师大版数学
一、单选题
1.菱形具有而一般矩形不具有的性质是( )
A.对边相等 B.对角线相等 C.对角线互相平分 D.对角线互相垂直
2.矩形的两条对角线相交于点O,,,则矩形对角线长( )
A. B. C. D.
3.下列命题中,假命题是( )
A.对角线相等的平行四边形是矩形
B.对角线互相垂直且平分的四边形是菱形
C.对角线相等且垂直的四边形是正方形
D.对角线互相平分的四边形是平行四边形
4.如图,将正方形放在平面直角坐标系中,O是坐标原点,点,则点F的坐标为( )
A. B. C. D.
5.如图,在正方形中,点、分别在、上(不与端点重合),连接、相交于点,BF=CE,则下列结论不正确的是( )
A. B.
C. D.
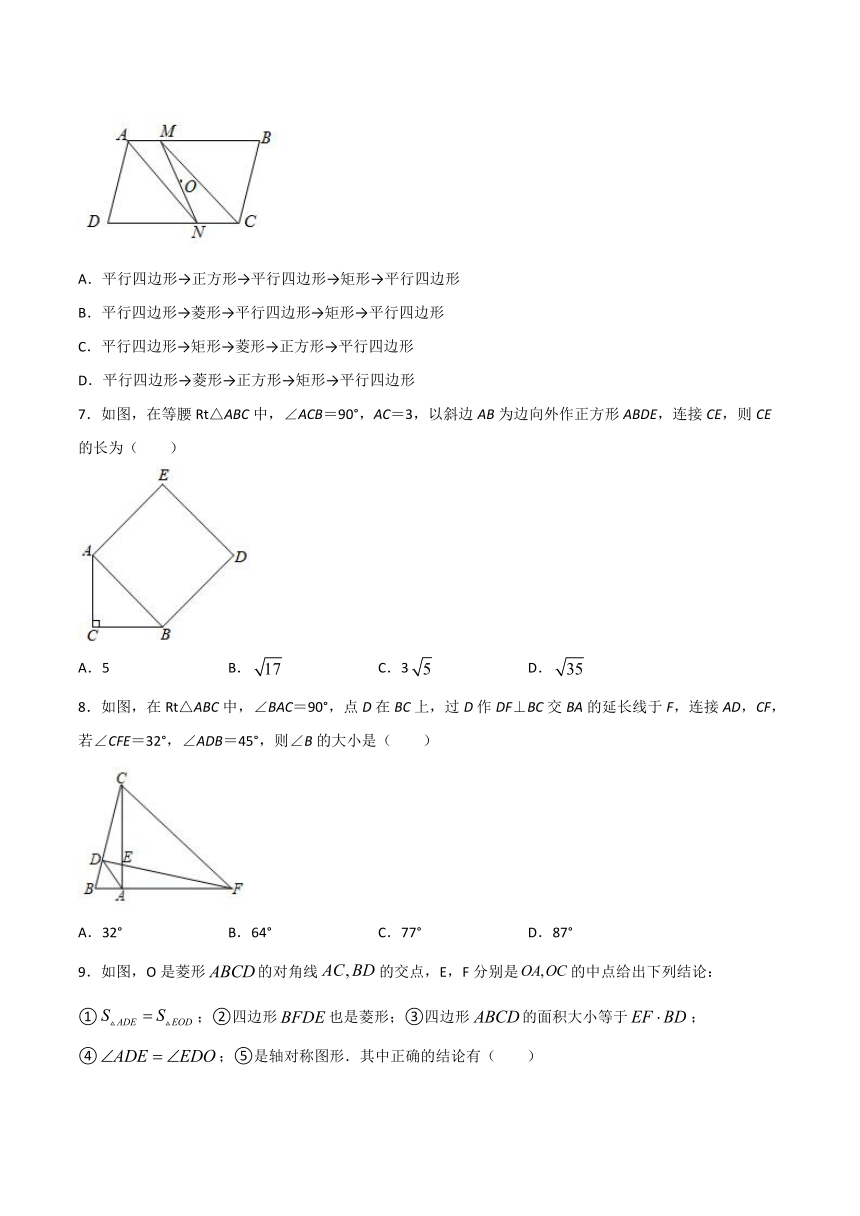
6.如图,在平行四边形ABCD中,∠DAB=120°,AB=4,AD=2,点O为对称中心,点M从点A出发沿AB向点B运动,到点B停止运动,连接MO并延长交CD于点N,则四边形AMCN形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形→平行四边形
B.平行四边形→菱形→平行四边形→矩形→平行四边形
C.平行四边形→矩形→菱形→正方形→平行四边形
D.平行四边形→菱形→正方形→矩形→平行四边形
7.如图,在等腰Rt△ABC中,∠ACB=90°,AC=3,以斜边AB为边向外作正方形ABDE,连接CE,则CE的长为( )
A.5 B. C.3 D.
8.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
9.如图,O是菱形的对角线的交点,E,F分别是的中点给出下列结论:①;②四边形也是菱形;③四边形的面积大小等于;④;⑤是轴对称图形.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
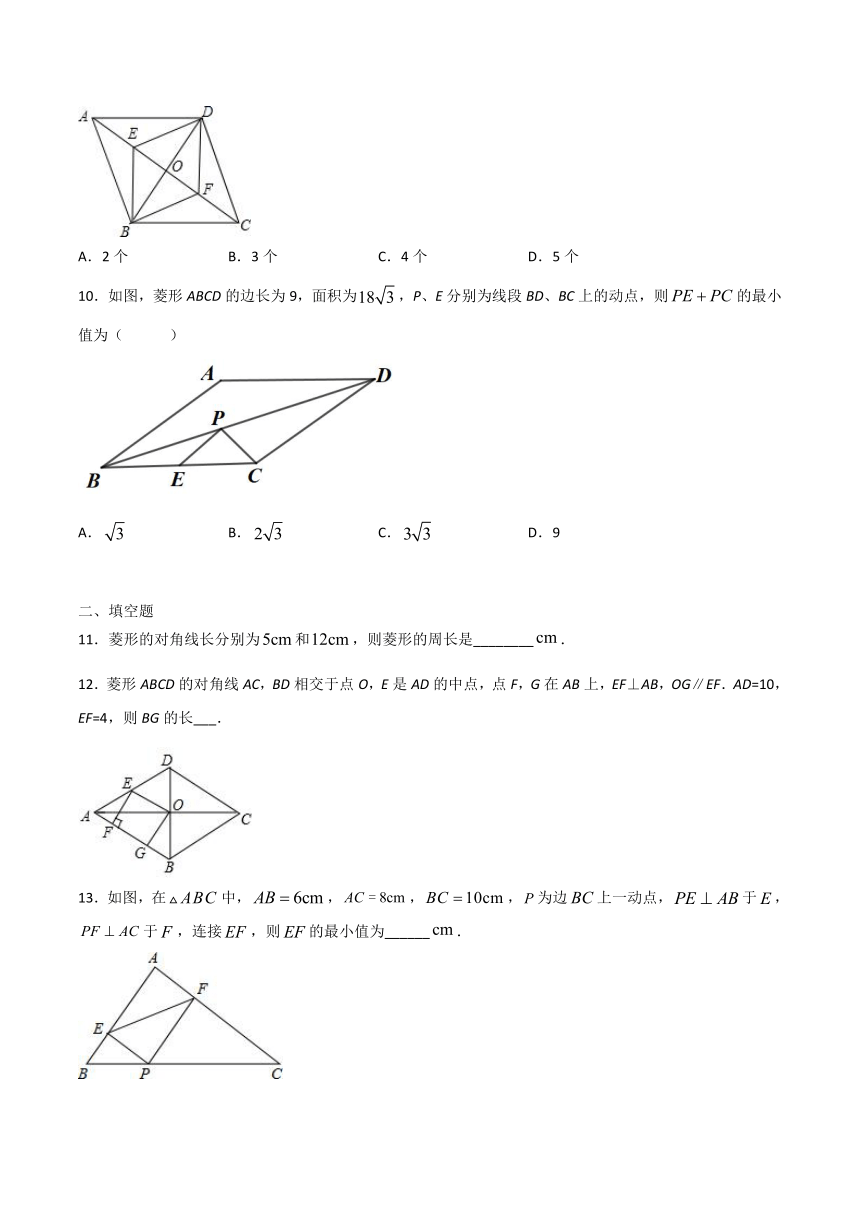
10.如图,菱形ABCD的边长为9,面积为,P、E分别为线段BD、BC上的动点,则的最小值为( )
A. B. C. D.9
二、填空题
11.菱形的对角线长分别为和,则菱形的周长是________.
12.菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.AD=10,EF=4,则BG的长___.
13.如图,在中,,,,为边上一动点,于,于,连接,则的最小值为______.
14.如图所示,把长方形放在直角坐标系中,使、分别落在x轴、y轴上,点C的坐标为,将沿翻折,使C点落在该坐标平面内的D点处,交x轴于点E.则点D的坐标为________.
15.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为__________.
16.如图,在中,,,,点E为边上的一个动点,连接,, 以、为邻边构造,连接,则的最小值为__________.
三、解答题
17.如图,在一正方形中,E为对角线上一点,连接、.
(1)求证:.
(2)延长交于点F,若.求的度数.
18.如图,已知矩形中,E是上一点,F是上的一点,,且.
(1)求证:.
(2)若,矩形的周长为,求的长.
19.已知,点E在正方形ABCD的AB边上(不与点A,B重合),BD是对角线,延长AB到点F,使BF=AE,过点E作BD的垂线,垂足为M,连接AM,CF.
(1)根据题意补全图形,并证明MB=ME;
(2)①用等式表示线段AM与CF的数量关系,并证明;
②直接用等式表示线段AM,BM,DM之间的数量关系.
20.已知:如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别相交于点E、F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?并给出证明.
21.如图,在平行四边形中,的平分线交于点,交的延长线于F,以为邻边作平行四边形.
(1)证明平行四边形是菱形;
(2)若,连结,
①求证:;
②求的度数;
(3)若,,,M是的中点,求的长.
22.如图1,以平行四边形的顶点O为坐标原点,以所在直线为x轴,建立平面直角坐标系,,D是对角线的中点,点P从点A出发,以每秒1个单位的速度沿方向运动到点B,同时点Q从点O出发,以每秒3个单位的速度沿x轴正方向运动,当点P到达点B时,两个点同时停止运动.
(1)求点A的坐标.
(2)连结,,,当经过点D时,求四边形的面积.
(3)在坐标系中找点F,使以Q、D、C、F为顶点的四边形是菱形,则点F的坐标为________.(直接写出答案)
参考答案
1.D2.B3.C4.A5.B6.B7.C8.C9.C10.B
11.12.213.14.15.4或1416.
17.(2)60°
18.(2)7cm
19.(2)①,证明见解析;②
20.(2)当EF⊥AC时,四边形AECF是菱形.证明见解析
21.②60°;(3)
22.(1);(2)21;(3)或或或
一、单选题
1.菱形具有而一般矩形不具有的性质是( )
A.对边相等 B.对角线相等 C.对角线互相平分 D.对角线互相垂直
2.矩形的两条对角线相交于点O,,,则矩形对角线长( )
A. B. C. D.
3.下列命题中,假命题是( )
A.对角线相等的平行四边形是矩形
B.对角线互相垂直且平分的四边形是菱形
C.对角线相等且垂直的四边形是正方形
D.对角线互相平分的四边形是平行四边形
4.如图,将正方形放在平面直角坐标系中,O是坐标原点,点,则点F的坐标为( )
A. B. C. D.
5.如图,在正方形中,点、分别在、上(不与端点重合),连接、相交于点,BF=CE,则下列结论不正确的是( )
A. B.
C. D.
6.如图,在平行四边形ABCD中,∠DAB=120°,AB=4,AD=2,点O为对称中心,点M从点A出发沿AB向点B运动,到点B停止运动,连接MO并延长交CD于点N,则四边形AMCN形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形→平行四边形
B.平行四边形→菱形→平行四边形→矩形→平行四边形
C.平行四边形→矩形→菱形→正方形→平行四边形
D.平行四边形→菱形→正方形→矩形→平行四边形
7.如图,在等腰Rt△ABC中,∠ACB=90°,AC=3,以斜边AB为边向外作正方形ABDE,连接CE,则CE的长为( )
A.5 B. C.3 D.
8.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
9.如图,O是菱形的对角线的交点,E,F分别是的中点给出下列结论:①;②四边形也是菱形;③四边形的面积大小等于;④;⑤是轴对称图形.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
10.如图,菱形ABCD的边长为9,面积为,P、E分别为线段BD、BC上的动点,则的最小值为( )
A. B. C. D.9
二、填空题
11.菱形的对角线长分别为和,则菱形的周长是________.
12.菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.AD=10,EF=4,则BG的长___.
13.如图,在中,,,,为边上一动点,于,于,连接,则的最小值为______.
14.如图所示,把长方形放在直角坐标系中,使、分别落在x轴、y轴上,点C的坐标为,将沿翻折,使C点落在该坐标平面内的D点处,交x轴于点E.则点D的坐标为________.
15.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为__________.
16.如图,在中,,,,点E为边上的一个动点,连接,, 以、为邻边构造,连接,则的最小值为__________.
三、解答题
17.如图,在一正方形中,E为对角线上一点,连接、.
(1)求证:.
(2)延长交于点F,若.求的度数.
18.如图,已知矩形中,E是上一点,F是上的一点,,且.
(1)求证:.
(2)若,矩形的周长为,求的长.
19.已知,点E在正方形ABCD的AB边上(不与点A,B重合),BD是对角线,延长AB到点F,使BF=AE,过点E作BD的垂线,垂足为M,连接AM,CF.
(1)根据题意补全图形,并证明MB=ME;
(2)①用等式表示线段AM与CF的数量关系,并证明;
②直接用等式表示线段AM,BM,DM之间的数量关系.
20.已知:如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别相交于点E、F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A、E、C、F为顶点的四边形是菱形?并给出证明.
21.如图,在平行四边形中,的平分线交于点,交的延长线于F,以为邻边作平行四边形.
(1)证明平行四边形是菱形;
(2)若,连结,
①求证:;
②求的度数;
(3)若,,,M是的中点,求的长.
22.如图1,以平行四边形的顶点O为坐标原点,以所在直线为x轴,建立平面直角坐标系,,D是对角线的中点,点P从点A出发,以每秒1个单位的速度沿方向运动到点B,同时点Q从点O出发,以每秒3个单位的速度沿x轴正方向运动,当点P到达点B时,两个点同时停止运动.
(1)求点A的坐标.
(2)连结,,,当经过点D时,求四边形的面积.
(3)在坐标系中找点F,使以Q、D、C、F为顶点的四边形是菱形,则点F的坐标为________.(直接写出答案)
参考答案
1.D2.B3.C4.A5.B6.B7.C8.C9.C10.B
11.12.213.14.15.4或1416.
17.(2)60°
18.(2)7cm
19.(2)①,证明见解析;②
20.(2)当EF⊥AC时,四边形AECF是菱形.证明见解析
21.②60°;(3)
22.(1);(2)21;(3)或或或
