2020-2021学年八年级数学华东师大版下册同步训练:第二十章 数据的整理与初步处理(word版含解析)
文档属性
| 名称 | 2020-2021学年八年级数学华东师大版下册同步训练:第二十章 数据的整理与初步处理(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 265.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 08:52:42 | ||
图片预览



文档简介
2020-2021学年八年级数学华东师大版下册同步训练:第二十章
数据的整理与初步处理
一、选择题(每小题4分,共32分)
1.为迎接中考体育考试,小刚和小亮分别统计了自己最近10次跳绳成绩,下列统计量中能用来比较两人成绩稳定程度的是
( )
A.平均数
B.中位数
C.众数
D.方差
2.某同学记录了自己一周每天的零花钱(单位:元),分别记录如下:5,4.5,5,5.5,5.5,5,4.5.
这组数据的众数和平均数分别是
( )
A.5和5.5
B.5和5
C.5和
D.和5.5
3.某校八年级甲、乙两班学生在一学期里进行了多次数学检测,计算多次检测的成绩发现两班的平均成绩相等,甲班成绩的方差大于乙班成绩的方差,则下列说法正确的是
( )
A.两班学生的数学学一样
B.甲班学生的学习潜力大
C.乙班数学成绩稳定
D.甲班的各次数学成绩比较接近
4.为了了解家庭日常消费情况,小松记录了她家一年中7周的日常生活消费费用(单位:元),数据如下:485,459,490,585,525,520,485.小松家这7周平均每周的日常生活费用为
( )
A.490元
B.500元
C.507元
D.510元
5.小莹同学10个周的综合素质评价成绩统计如下:
成绩(分)
94
95
97
98
100
周数
1
2
2
4
1
这10个周的综合素质评价成绩的中位数和方差分别是
( )
A.97.5分,2.8
B.97.5分,3
C.97分,2.8
D.97分,3
6.已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b的值为
( )
A.98
B.99
C.100
D.102
7.学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下表:
售价
3元
4元
5元
6元
数目
14本
11本
10本
15本
下列说法正确的是
( )
A.该班级所售图书的总收入是226元
B.在该班级所售图书价格组成的一组数据中,中位数是4
C.在该班级所售图书价格组成的一组数据中,众数是15
D.在该班级所售图书价格组成的一组数据中,方差是2
8.在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )
A.11
B.12
C.13
D.14
二、填空题(每小题4分,共24分)
9.有一组数据:5,4,3,6,7,则这组数据的方差是 .?
10.春天服饰店销售5种领口尺寸分别为38
cm,39
cm,40
cm,41
cm,42
cm的衬衫,为了了解各种领口尺寸衬衫的销售情况,服饰店统计了某月的销售情况如下表:
领口尺寸/cm
38
39
40
41
42
销售量/件
13
19
34
15
9
若你是此服饰店的老板,你最关心各种领口尺寸衬衫的销售量的 (填“平均数”“众数”或“中位数”).?
11.玲玲上学期九门科目的期末考试成绩(单位:分)分别是95,90,90,x,86,87,81,92,88.若平均分是89分,则x= .?
12.已知学生的学科期末成绩由期末分数、作业分数、课堂参与分数三部分组成,并按4∶3∶3的比例确定.若小明的数学期末分数为85分,作业分数为90分,课堂参与分数为80分,则他的数学期末成绩为 .?
13.已知一组数据x1,x2,x3,…,xn的方差为2,则另一组数据3x1,3x2,3x3,…,3xn的方差为 .?
14.某公司全体员工年薪的具体情况如下表:
年薪(万元)
30
14
9
6
4
3.5
3
员工数(人)
1
1
1
2
7
6
2
则该公司全体员工年薪的平均数比中位数多 万元.?
三、解答题(共44分)
15.(14分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
16.(14分)在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图(如图)如下:
命中环数
10
9
8
7
命中次数
3
2
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
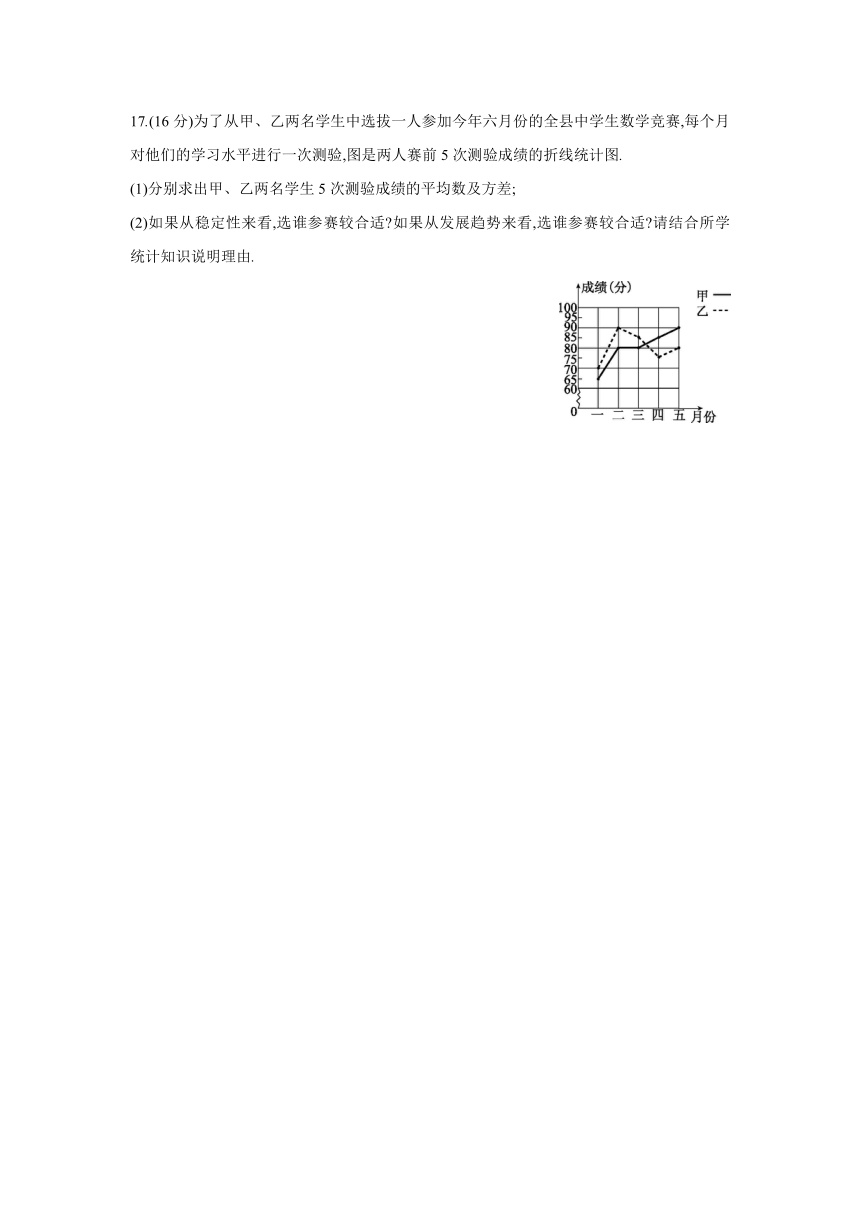
17.(16分)为了从甲、乙两名学生中选拔一人参加今年六月份的全县中学生数学竞赛,每个月对他们的学进行一次测验,图是两人赛前5次测验成绩的折线统计图.
(1)分别求出甲、乙两名学生5次测验成绩的平均数及方差;
(2)如果从稳定性来看,选谁参赛较合适?如果从发展趋势来看,选谁参赛较合适?请结合所学统计知识说明理由.
教师详解详析
作者说卷
随着科学技术的不断发展,统计的应用越来越广泛.本章是统计初步的重要章节,针对反映数据情况的特征,分别对样本的平均数、中位数、众数、方差做了详细的介绍.因本章与实际生活联系紧密,在选题中,注重联系实际以提高学生解决实际问题的能力,并注意与中考接轨,不出现偏题、怪题.
涉及的相关内容有:
类别
题号
知识与技能
平均数与加权平均数
2,4,11,12,14,15,17
中位数、众数
2,5,6,7,8,10,14
方差
1,3,5,6,7,9,13,16,17
思想方法
统计思想
16
转化思想
13
亮点
能将本章所学知识很好地运用到生活实际中去,从而提高学生的学习兴趣与解决问题的本领
4,12
1.D
2.B [解析]
5出现了三次,出现次数最多,
所以这组数据的众数是5,
这组数据的平均数=(5+4.5+5+5.5+5.5+5+4.5)=5.
故选B.
3.C
4.C [解析]
=507(元).
5.B [解析]
成绩总共10个数,按从小到大排序后中间两个数为97和98,故中位数为97.5分;这10个数的平均数=×(94+95×2+97×2+98×4+100)=97(分),故其方差为[(94-97)2+(95-97)2×2+(97-97)2×2+(98-97)2×4+(100-97)2]=3.故选B.
6.C [解析]
将数据92,94,98,91,95按从小到大的顺序排列为91,92,94,95,98,处于中间位置的数是94.
则该组数据的中位数是94,即a=94.
该组数据的平均数为×(92+94+98+91+95)=94,
其方差为[(92-94)2+(94-94)2+(98-94)2+(91-94)2+(95-94)2]=6,所以b=6,
所以a+b=94+6=100.故选C.
7.A [解析]
A选项,该班级所售图书的总收入为3×14+4×11+5×10+6×15=226(元),∴A选项正确;
B选项,第25个数为4,第26个数为5,∴这组数据的中位数为4.5,∴B选项错误;
C选项,这组数据的众数为6,∴C选项错误;
D选项,这组数据的平均数==4.52,
∴这组数据的方差=[14(3-4.52)2+11(4-4.52)2+10(5-4.52)2+15(6-4.52)2]≈1.4,
∴D选项错误.故选A.
8.A [解析]
因为五个整数从小到大排列后,其中位数是2,这组数据的唯一众数是4,所以这5个数据分别是x,y,2,4,4,且x9.2 10.众数
11.92 [解析]
(95+90+90+x+86+87+81+92+88)÷9=89,解得x=92.
12.85分 [解析]
期末成绩为(85×4+90×3+80×3)÷(4+3+3)=85(分).
13.18 [解析]
∵一组数据x1,x2,x3,…,xn的方差为2,∴另一组数据3x1,3x2,3x3,…,3xn的方差为32×2=18.故答案为18.
14.2
15.解:(1)这四名候选人面试成绩的中位数为=89(分).
(2)由题意,得x×60%+90×40%=87.6.
解得x=86,
答:表中x的值为86.
(3)甲候选人的综合成绩为90×60%+88×40%=89.2(分),
乙候选人的综合成绩为84×60%+92×40%=87.2(分),
丁候选人的综合成绩为88×60%+86×40%=87.2(分).
89.2>87.6>87.2=87.2,
所以以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
16.解:(1)命中环数是7环的次数是10×10%=1(次),命中环数是10环的次数是10-3-2-1=4(次),
命中环数是8环的圆心角度数是360°×=72°,命中环数是10环的圆心角度数是360°×=144°,
补全扇形统计图如图.
统计表中依次填4,1.
(2)应该派甲去.
理由:∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9(环),
∴甲运动员10次射击成绩的方差为×[(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1.
∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲运动员10次射击成绩的方差,
∴如果只能选一人参加比赛,应该派甲去.
17.解:(1)甲、乙测验成绩的平均数分别是
=×(65+80+80+85+90)=80(分),
=×(70+90+85+75+80)=80(分).
甲的方差为[(65-80)2+(80-80)2+(80-80)2+(85-80)2+(90-80)2]=70,
乙的方差为[(70-80)2+(90-80)2+(85-80)2+(75-80)2+(80-80)2]=50.
(2)观察(1)中计算的结果,可知甲、乙两人5次测试成绩的平均数一样,甲的方差大于乙的方差,说明乙这5次的成绩比较稳定,所以从稳定性来看,选乙参赛较合适;从发展趋势来看,甲后两次成绩呈上升趋势,且比乙好,而乙的成绩有所下降,所以从发展趋势来看,选甲参赛较合适(言之有理即可).
数据的整理与初步处理
一、选择题(每小题4分,共32分)
1.为迎接中考体育考试,小刚和小亮分别统计了自己最近10次跳绳成绩,下列统计量中能用来比较两人成绩稳定程度的是
( )
A.平均数
B.中位数
C.众数
D.方差
2.某同学记录了自己一周每天的零花钱(单位:元),分别记录如下:5,4.5,5,5.5,5.5,5,4.5.
这组数据的众数和平均数分别是
( )
A.5和5.5
B.5和5
C.5和
D.和5.5
3.某校八年级甲、乙两班学生在一学期里进行了多次数学检测,计算多次检测的成绩发现两班的平均成绩相等,甲班成绩的方差大于乙班成绩的方差,则下列说法正确的是
( )
A.两班学生的数学学一样
B.甲班学生的学习潜力大
C.乙班数学成绩稳定
D.甲班的各次数学成绩比较接近
4.为了了解家庭日常消费情况,小松记录了她家一年中7周的日常生活消费费用(单位:元),数据如下:485,459,490,585,525,520,485.小松家这7周平均每周的日常生活费用为
( )
A.490元
B.500元
C.507元
D.510元
5.小莹同学10个周的综合素质评价成绩统计如下:
成绩(分)
94
95
97
98
100
周数
1
2
2
4
1
这10个周的综合素质评价成绩的中位数和方差分别是
( )
A.97.5分,2.8
B.97.5分,3
C.97分,2.8
D.97分,3
6.已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b的值为
( )
A.98
B.99
C.100
D.102
7.学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下表:
售价
3元
4元
5元
6元
数目
14本
11本
10本
15本
下列说法正确的是
( )
A.该班级所售图书的总收入是226元
B.在该班级所售图书价格组成的一组数据中,中位数是4
C.在该班级所售图书价格组成的一组数据中,众数是15
D.在该班级所售图书价格组成的一组数据中,方差是2
8.在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )
A.11
B.12
C.13
D.14
二、填空题(每小题4分,共24分)
9.有一组数据:5,4,3,6,7,则这组数据的方差是 .?
10.春天服饰店销售5种领口尺寸分别为38
cm,39
cm,40
cm,41
cm,42
cm的衬衫,为了了解各种领口尺寸衬衫的销售情况,服饰店统计了某月的销售情况如下表:
领口尺寸/cm
38
39
40
41
42
销售量/件
13
19
34
15
9
若你是此服饰店的老板,你最关心各种领口尺寸衬衫的销售量的 (填“平均数”“众数”或“中位数”).?
11.玲玲上学期九门科目的期末考试成绩(单位:分)分别是95,90,90,x,86,87,81,92,88.若平均分是89分,则x= .?
12.已知学生的学科期末成绩由期末分数、作业分数、课堂参与分数三部分组成,并按4∶3∶3的比例确定.若小明的数学期末分数为85分,作业分数为90分,课堂参与分数为80分,则他的数学期末成绩为 .?
13.已知一组数据x1,x2,x3,…,xn的方差为2,则另一组数据3x1,3x2,3x3,…,3xn的方差为 .?
14.某公司全体员工年薪的具体情况如下表:
年薪(万元)
30
14
9
6
4
3.5
3
员工数(人)
1
1
1
2
7
6
2
则该公司全体员工年薪的平均数比中位数多 万元.?
三、解答题(共44分)
15.(14分)某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
16.(14分)在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图(如图)如下:
命中环数
10
9
8
7
命中次数
3
2
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
17.(16分)为了从甲、乙两名学生中选拔一人参加今年六月份的全县中学生数学竞赛,每个月对他们的学进行一次测验,图是两人赛前5次测验成绩的折线统计图.
(1)分别求出甲、乙两名学生5次测验成绩的平均数及方差;
(2)如果从稳定性来看,选谁参赛较合适?如果从发展趋势来看,选谁参赛较合适?请结合所学统计知识说明理由.
教师详解详析
作者说卷
随着科学技术的不断发展,统计的应用越来越广泛.本章是统计初步的重要章节,针对反映数据情况的特征,分别对样本的平均数、中位数、众数、方差做了详细的介绍.因本章与实际生活联系紧密,在选题中,注重联系实际以提高学生解决实际问题的能力,并注意与中考接轨,不出现偏题、怪题.
涉及的相关内容有:
类别
题号
知识与技能
平均数与加权平均数
2,4,11,12,14,15,17
中位数、众数
2,5,6,7,8,10,14
方差
1,3,5,6,7,9,13,16,17
思想方法
统计思想
16
转化思想
13
亮点
能将本章所学知识很好地运用到生活实际中去,从而提高学生的学习兴趣与解决问题的本领
4,12
1.D
2.B [解析]
5出现了三次,出现次数最多,
所以这组数据的众数是5,
这组数据的平均数=(5+4.5+5+5.5+5.5+5+4.5)=5.
故选B.
3.C
4.C [解析]
=507(元).
5.B [解析]
成绩总共10个数,按从小到大排序后中间两个数为97和98,故中位数为97.5分;这10个数的平均数=×(94+95×2+97×2+98×4+100)=97(分),故其方差为[(94-97)2+(95-97)2×2+(97-97)2×2+(98-97)2×4+(100-97)2]=3.故选B.
6.C [解析]
将数据92,94,98,91,95按从小到大的顺序排列为91,92,94,95,98,处于中间位置的数是94.
则该组数据的中位数是94,即a=94.
该组数据的平均数为×(92+94+98+91+95)=94,
其方差为[(92-94)2+(94-94)2+(98-94)2+(91-94)2+(95-94)2]=6,所以b=6,
所以a+b=94+6=100.故选C.
7.A [解析]
A选项,该班级所售图书的总收入为3×14+4×11+5×10+6×15=226(元),∴A选项正确;
B选项,第25个数为4,第26个数为5,∴这组数据的中位数为4.5,∴B选项错误;
C选项,这组数据的众数为6,∴C选项错误;
D选项,这组数据的平均数==4.52,
∴这组数据的方差=[14(3-4.52)2+11(4-4.52)2+10(5-4.52)2+15(6-4.52)2]≈1.4,
∴D选项错误.故选A.
8.A [解析]
因为五个整数从小到大排列后,其中位数是2,这组数据的唯一众数是4,所以这5个数据分别是x,y,2,4,4,且x
11.92 [解析]
(95+90+90+x+86+87+81+92+88)÷9=89,解得x=92.
12.85分 [解析]
期末成绩为(85×4+90×3+80×3)÷(4+3+3)=85(分).
13.18 [解析]
∵一组数据x1,x2,x3,…,xn的方差为2,∴另一组数据3x1,3x2,3x3,…,3xn的方差为32×2=18.故答案为18.
14.2
15.解:(1)这四名候选人面试成绩的中位数为=89(分).
(2)由题意,得x×60%+90×40%=87.6.
解得x=86,
答:表中x的值为86.
(3)甲候选人的综合成绩为90×60%+88×40%=89.2(分),
乙候选人的综合成绩为84×60%+92×40%=87.2(分),
丁候选人的综合成绩为88×60%+86×40%=87.2(分).
89.2>87.6>87.2=87.2,
所以以综合成绩排序确定所要招聘的前两名的人选是甲和丙.
16.解:(1)命中环数是7环的次数是10×10%=1(次),命中环数是10环的次数是10-3-2-1=4(次),
命中环数是8环的圆心角度数是360°×=72°,命中环数是10环的圆心角度数是360°×=144°,
补全扇形统计图如图.
统计表中依次填4,1.
(2)应该派甲去.
理由:∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9(环),
∴甲运动员10次射击成绩的方差为×[(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1.
∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲运动员10次射击成绩的方差,
∴如果只能选一人参加比赛,应该派甲去.
17.解:(1)甲、乙测验成绩的平均数分别是
=×(65+80+80+85+90)=80(分),
=×(70+90+85+75+80)=80(分).
甲的方差为[(65-80)2+(80-80)2+(80-80)2+(85-80)2+(90-80)2]=70,
乙的方差为[(70-80)2+(90-80)2+(85-80)2+(75-80)2+(80-80)2]=50.
(2)观察(1)中计算的结果,可知甲、乙两人5次测试成绩的平均数一样,甲的方差大于乙的方差,说明乙这5次的成绩比较稳定,所以从稳定性来看,选乙参赛较合适;从发展趋势来看,甲后两次成绩呈上升趋势,且比乙好,而乙的成绩有所下降,所以从发展趋势来看,选甲参赛较合适(言之有理即可).
