2020-2021学年下学期华东师大版九年级数学下册 26.3 实践与探索(培优卷)(word版含答案)
文档属性
| 名称 | 2020-2021学年下学期华东师大版九年级数学下册 26.3 实践与探索(培优卷)(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 07:47:59 | ||
图片预览


文档简介
26.3实践与探索(培优卷)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知函数的图象与x轴有交点.则的取值范围是(
)
A.k<4
B.k≤4
C.k<4且k≠3
D.k≤4且k≠3
2.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为元时,获得的利润为元,则下列关系式正确的是(
)
A.
B.
C.
D.
3.小明在一次训练中,掷出的实心球飞行高度(米)与水平距离(米)之间的关系大致满足二次函数,则小明此次成绩为(
)
A.8米
B.10米
C.12米
D.14米
4.抛物线y=x2+2bx与x轴的两个不同交点是O和A,顶点B在直线y=kx上,若△OAB是等边三角形,则b=( )
A.±
B.±3
C.±
D.±
5.某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度与水平距离之间的函数关系式是,则水池在喷水过程中水流的最大高度为(
)
A.1.25米
B.2.25米
C.2.5米
D.3米
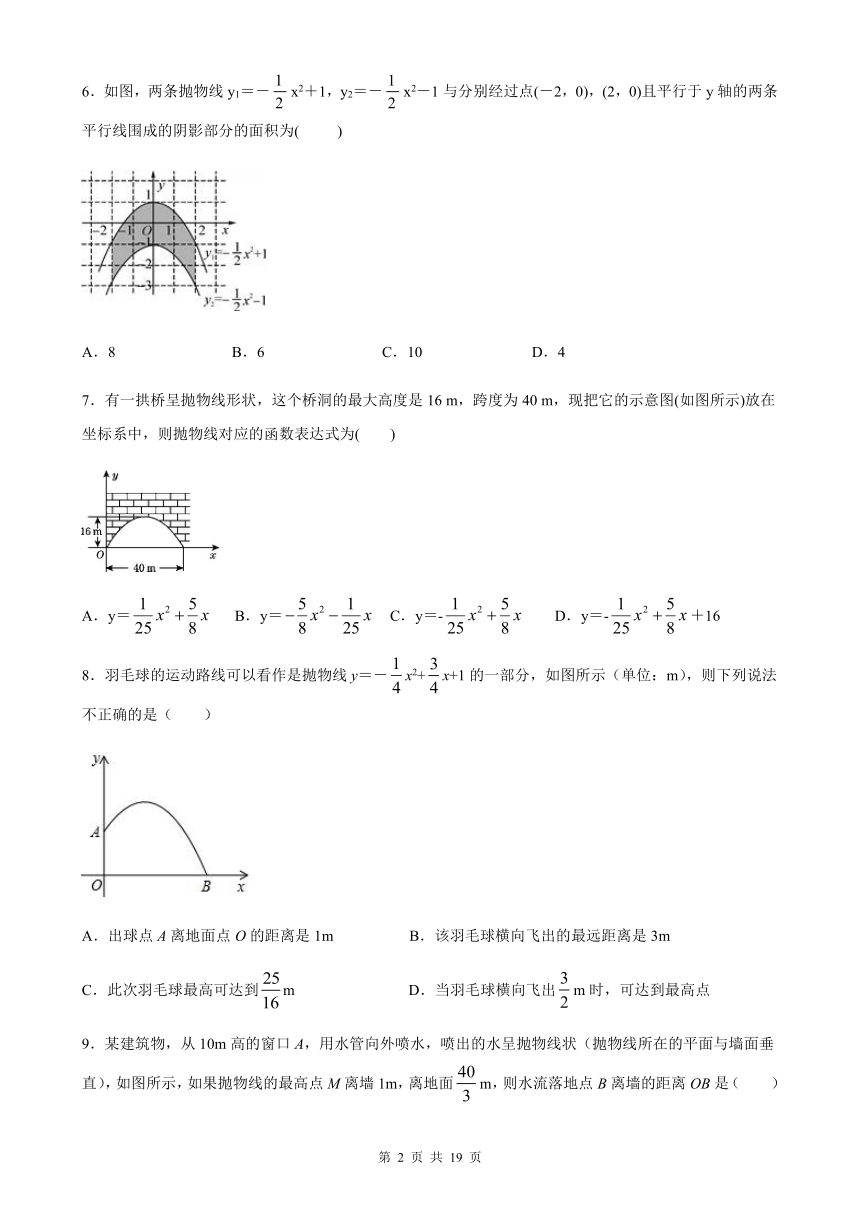
6.如图,两条抛物线y1=-x2+1,y2=-x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为(
)
A.8
B.6
C.10
D.4
7.有一拱桥呈抛物线形状,这个桥洞的最大高度是16
m,跨度为40
m,现把它的示意图(如图所示)放在坐标系中,则抛物线对应的函数表达式为( )
A.y=
B.y=
C.y=-
D.y=-+16
8.羽毛球的运动路线可以看作是抛物线y=-x2+x+1的一部分,如图所示(单位:m),则下列说法不正确的是(
)
A.出球点A离地面点O的距离是1m
B.该羽毛球横向飞出的最远距离是3m
C.此次羽毛球最高可达到m
D.当羽毛球横向飞出m时,可达到最高点
9.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是(
)
A.2m
B.3m
C.4m
D.5m
10.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A.
B.
C.
D.
11.如图,抛物线与x轴一个交点为,对称轴为直线,则时x的范围是
A.或
B.
C.
D.
12.如图,是二次函数图象的一部分,下列结论中:①;②;③有两个相等的实数根;④.其中正确结论的序号为(
)
A.①②
B.①③
C.②③
D.①④
二、填空题
13.用一根长为的铁丝围成一个矩形,该矩形面积的最大值是__________.
14.二次函数中的自变量与函数值的部分对应值如下表:
…
…
…
…
则的解为________.
15.如图,正方形的顶点在边长为的正方形的边上,若设,正方形的面积为,则与的函数关系为________________________(写出自变量的取值范围).
16.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为________?m2
.
17.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m的解集为______________.
18.如图,在△ABC中,BC=8,高AD=6,矩形EFGH的一边EF在边BC上,其余两个顶点G、H分别在边AC、AB上,则矩形EFGH的面积最大值为_____.
三、解答题
19.某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
20.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?
21.已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D,
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
22.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=S△BCD,求点P的坐标.
23.如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
24.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值;
(3)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请写出所符合条件的点M的坐标;若不存在,请说明理由.
25.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
B
B
A
B
A
C
B
B
A
B
D
二、填空题
13
14
15
16
17
18
X=-2或1
y=2x2-4x+4(0<x<2)
75
x<1或x>3
12
三、解答题
19.
(1)设y与x的函数关系式为y=kx+b.
把(22,36)与(24,32)代入,得
解得
∴y=-2x+80(20≤x≤28)
(2)设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x元,根据题意,得
(x-20)y=150,即(x-20)(-2x+80)=150.
解得x1=25,x2=35(舍去).
答:每本纪念册的销售单价是25元.
(3)由题意,可得w=(x-20)(-2x+80)=-2(x-30)2+200.
∵售价不低于20元且不高于28元,
当x<30时,y随x的增大而增大,
∴当x=28时,w最大=-2×(28-30)2+200=192(元).
答:该纪念册销售单价定为28元时,能使文具店销售该纪念册所获利润最大,最大利润是192元.
20.
解:(1)根据题意,得S=x(24﹣3x),
即所求的函数解析式为:S=﹣3x2+24x,
又∵0<24﹣3x≤10,
∴;
(2)根据题意,设花圃宽AB为xm,则长为(24-3x),
∴﹣3x2+24x=45.
整理,得x2﹣8x+15=0,
解得x=3或5,
当x=3时,长=24﹣9=15>10不成立,
当x=5时,长=24﹣15=9<10成立,
∴AB长为5m;
(3)S=24x﹣3x2=﹣3(x﹣4)2+48
∵墙的最大可用长度为10m,0≤24﹣3x≤10,
∴,
∵对称轴x=4,开口向下,
∴当x=m,有最大面积的花圃.
21.
(1)∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),
∴将A(﹣1,0)、C(0,3),代入,
得,解得,
∴抛物线的解析式为y=﹣x2+2x+3;
如图,连接DC、BC、DB,由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),∴CD==,BC==3,BD==2,
∵CD2+BC2=()2+(3)2=20,BD2=(2)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
y=﹣x2+2x+3对称轴为直线x=1.假设存在这样的点P,
①
以CD为底边,则P1D=P1C,设P1点坐标为(x,y),
∵
根据勾股定理可得:P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,
∴
x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,
即y=4﹣x.
又∵
P1点(x,y)在抛物线上,
∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,
解得x1=,x2=<1,(不满足在对称轴右侧应舍去),
∴x=,∴y=4﹣x=,即点P1坐标为(,).
②
以CD为一腰,∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,此时点P2坐标为(2,3).
∴符合条件的点P坐标为(,)或(2,3).
22.
解:(1)、∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD=CD×|yB|=×4×3=6;
(3)由(2)知,S△BCD=CD×|yB|=×4×3=6;CD=4,
∵S△PCD=S△BCD,
∴S△PCD=CD×|yP|=×4×|yP|=3,
∴|yP|=
,
∵点P在x轴上方的抛物线上,
∴yP>0,
∴yP=
,
∵抛物线的解析式为y=﹣(x﹣1)2+4;
∴=﹣(x﹣1)2+4,
∴x=1±,
∴P(1+
,
),或P(1﹣,).
23.
解:(1)把A(3,0)B(0,-3)代入,得
解得
所以抛物线的解析式是.
设直线AB的解析式是,把A(3,0)B(0,)代入,得
解得
所以直线AB的解析式是.
(2)设点P的坐标是(),则M(,),因为在第四象限,所以PM=,当PM最长时,此时
==.
(3)若存在,则可能是:
①P在第四象限:平行四边形OBMP
,PM=OB=3,
PM最长时,所以不可能.
②P在第一象限平行四边形OBPM:
PM=OB=3,,解得,(舍去),所以P点的横坐标是.
③P在第三象限平行四边形OBPM:PM=OB=3,,解得(舍去),
①,所以P点的横坐标是.
所以P点的横坐标是或.
24.
解:(1)y=﹣x+3,令y=0,则x=3,令x=0,则y=3,
故点B、C的坐标为(3,0)、(0,3),
将点B、C的坐标代入y=x2+bx+c并解得:b=﹣4,
故抛物线的表达式为:y=x2﹣4x+3,
令y=0,则x=1或3,故点A(1,0),点P(2,﹣1);
(2)过点E作EH∥y轴交BC于点H,
设点E(x,x2﹣4x+3),则点H(x,﹣x+3)
S△CBE=HE×OB=×3×(﹣x+3﹣x2+4x﹣3)=(﹣x2+3x),
∵﹣<0,当x=时,S△CBE有最大值,
点E(,﹣);
(3)点C(0,3)、点P(2,﹣1),设点M(2,m),
CP2=4+16=20,CM2=4+(m﹣3)2=m2﹣6m+13,PM2=m2+2m+1,
①当CM=CP时,20=m2﹣6m+13,解得:m=7或﹣1(舍去m=﹣1);
②当CP=PM时,同理可得:m=﹣1±2;
③当CM=PM时,同理可得:m=;
故点M坐标为:(2,7)或(2,﹣1+2
=)或(2,﹣1﹣2)或(2,).
25.
(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3).
把y=0代入y=﹣x+3得:x=3,
∴B(3,0),A(﹣1,0).
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:
,解得b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图所示:作点O关于BC的对称点O′,则O′(3,3).
∵O′与O关于BC对称,
∴PO=PO′.
∴OP+AP=O′P+AP≤AO′.
∴OP+AP的最小值=O′A==5.
O′A的方程为y=
P点满足解得:
所以P
(
,)
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
又∵C(0,3,B(3,0),
∴CD=,BC=3,DB=2.
∴CD2+CB2=BD2,
∴∠DCB=90°.
∵A(﹣1,0),C(0,3),
∴OA=1,CO=3.
∴.
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图所示:连接AC,过点C作CQ⊥AC,交x轴与点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB.
∴,即,解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知函数的图象与x轴有交点.则的取值范围是(
)
A.k<4
B.k≤4
C.k<4且k≠3
D.k≤4且k≠3
2.将进货价为35元的商品按单价40元售出时,能卖出200个,已知该商品单价每上涨1元,其销售量就减少5个,设这种商品的售价为元时,获得的利润为元,则下列关系式正确的是(
)
A.
B.
C.
D.
3.小明在一次训练中,掷出的实心球飞行高度(米)与水平距离(米)之间的关系大致满足二次函数,则小明此次成绩为(
)
A.8米
B.10米
C.12米
D.14米
4.抛物线y=x2+2bx与x轴的两个不同交点是O和A,顶点B在直线y=kx上,若△OAB是等边三角形,则b=( )
A.±
B.±3
C.±
D.±
5.某公园一喷水池喷水时水流的路线呈抛物线(如图).若喷水时水流的高度与水平距离之间的函数关系式是,则水池在喷水过程中水流的最大高度为(
)
A.1.25米
B.2.25米
C.2.5米
D.3米
6.如图,两条抛物线y1=-x2+1,y2=-x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为(
)
A.8
B.6
C.10
D.4
7.有一拱桥呈抛物线形状,这个桥洞的最大高度是16
m,跨度为40
m,现把它的示意图(如图所示)放在坐标系中,则抛物线对应的函数表达式为( )
A.y=
B.y=
C.y=-
D.y=-+16
8.羽毛球的运动路线可以看作是抛物线y=-x2+x+1的一部分,如图所示(单位:m),则下列说法不正确的是(
)
A.出球点A离地面点O的距离是1m
B.该羽毛球横向飞出的最远距离是3m
C.此次羽毛球最高可达到m
D.当羽毛球横向飞出m时,可达到最高点
9.某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是(
)
A.2m
B.3m
C.4m
D.5m
10.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A.
B.
C.
D.
11.如图,抛物线与x轴一个交点为,对称轴为直线,则时x的范围是
A.或
B.
C.
D.
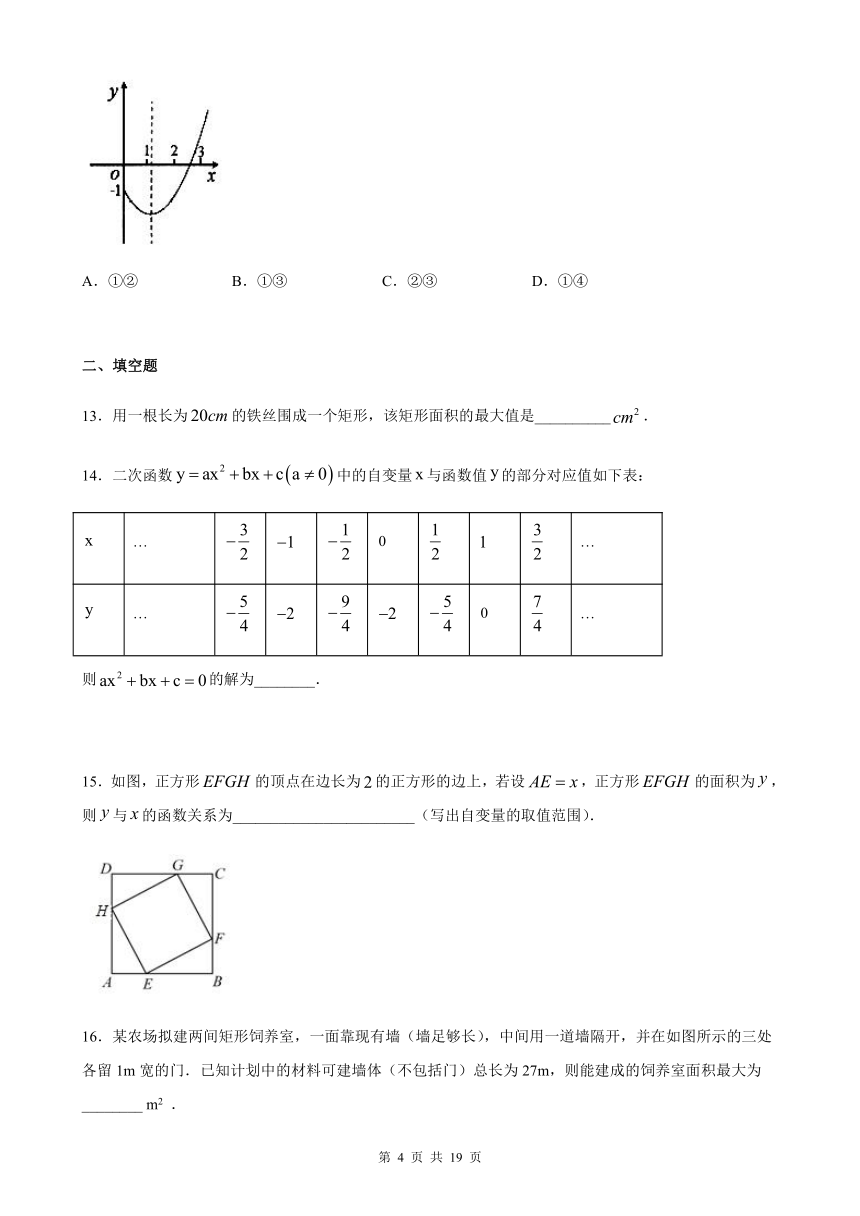
12.如图,是二次函数图象的一部分,下列结论中:①;②;③有两个相等的实数根;④.其中正确结论的序号为(
)
A.①②
B.①③
C.②③
D.①④
二、填空题
13.用一根长为的铁丝围成一个矩形,该矩形面积的最大值是__________.
14.二次函数中的自变量与函数值的部分对应值如下表:
…
…
…
…
则的解为________.
15.如图,正方形的顶点在边长为的正方形的边上,若设,正方形的面积为,则与的函数关系为________________________(写出自变量的取值范围).
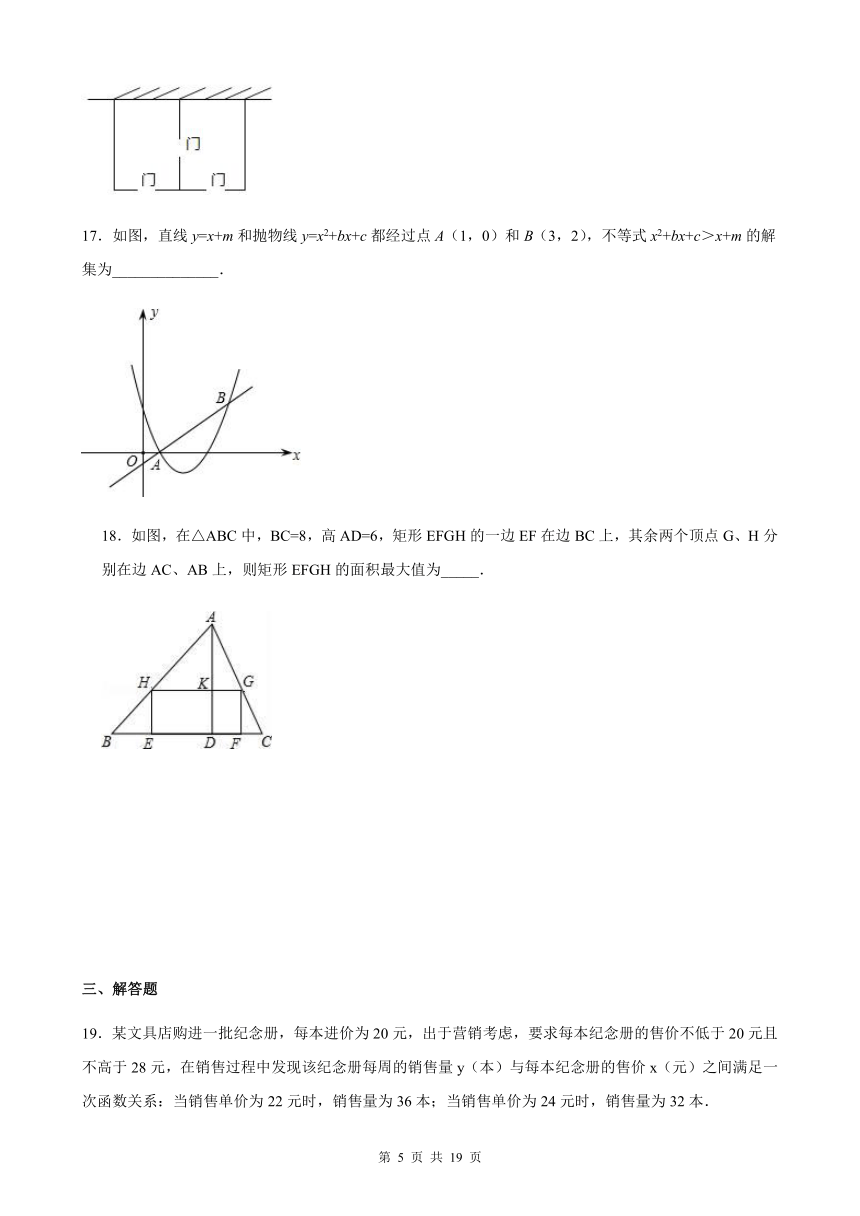
16.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为________?m2
.
17.如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0)和B(3,2),不等式x2+bx+c>x+m的解集为______________.
18.如图,在△ABC中,BC=8,高AD=6,矩形EFGH的一边EF在边BC上,其余两个顶点G、H分别在边AC、AB上,则矩形EFGH的面积最大值为_____.
三、解答题
19.某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
20.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45m2的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?
21.已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D,
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
22.如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=S△BCD,求点P的坐标.
23.如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
24.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值;
(3)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请写出所符合条件的点M的坐标;若不存在,请说明理由.
25.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
B
B
A
B
A
C
B
B
A
B
D
二、填空题
13
14
15
16
17
18
X=-2或1
y=2x2-4x+4(0<x<2)
75
x<1或x>3
12
三、解答题
19.
(1)设y与x的函数关系式为y=kx+b.
把(22,36)与(24,32)代入,得
解得
∴y=-2x+80(20≤x≤28)
(2)设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x元,根据题意,得
(x-20)y=150,即(x-20)(-2x+80)=150.
解得x1=25,x2=35(舍去).
答:每本纪念册的销售单价是25元.
(3)由题意,可得w=(x-20)(-2x+80)=-2(x-30)2+200.
∵售价不低于20元且不高于28元,
当x<30时,y随x的增大而增大,
∴当x=28时,w最大=-2×(28-30)2+200=192(元).
答:该纪念册销售单价定为28元时,能使文具店销售该纪念册所获利润最大,最大利润是192元.
20.
解:(1)根据题意,得S=x(24﹣3x),
即所求的函数解析式为:S=﹣3x2+24x,
又∵0<24﹣3x≤10,
∴;
(2)根据题意,设花圃宽AB为xm,则长为(24-3x),
∴﹣3x2+24x=45.
整理,得x2﹣8x+15=0,
解得x=3或5,
当x=3时,长=24﹣9=15>10不成立,
当x=5时,长=24﹣15=9<10成立,
∴AB长为5m;
(3)S=24x﹣3x2=﹣3(x﹣4)2+48
∵墙的最大可用长度为10m,0≤24﹣3x≤10,
∴,
∵对称轴x=4,开口向下,
∴当x=m,有最大面积的花圃.
21.
(1)∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),
∴将A(﹣1,0)、C(0,3),代入,
得,解得,
∴抛物线的解析式为y=﹣x2+2x+3;
如图,连接DC、BC、DB,由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),∴CD==,BC==3,BD==2,
∵CD2+BC2=()2+(3)2=20,BD2=(2)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
y=﹣x2+2x+3对称轴为直线x=1.假设存在这样的点P,
①
以CD为底边,则P1D=P1C,设P1点坐标为(x,y),
∵
根据勾股定理可得:P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,
∴
x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,
即y=4﹣x.
又∵
P1点(x,y)在抛物线上,
∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0,
解得x1=,x2=<1,(不满足在对称轴右侧应舍去),
∴x=,∴y=4﹣x=,即点P1坐标为(,).
②
以CD为一腰,∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,此时点P2坐标为(2,3).
∴符合条件的点P坐标为(,)或(2,3).
22.
解:(1)、∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4;
(2)由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD=CD×|yB|=×4×3=6;
(3)由(2)知,S△BCD=CD×|yB|=×4×3=6;CD=4,
∵S△PCD=S△BCD,
∴S△PCD=CD×|yP|=×4×|yP|=3,
∴|yP|=
,
∵点P在x轴上方的抛物线上,
∴yP>0,
∴yP=
,
∵抛物线的解析式为y=﹣(x﹣1)2+4;
∴=﹣(x﹣1)2+4,
∴x=1±,
∴P(1+
,
),或P(1﹣,).
23.
解:(1)把A(3,0)B(0,-3)代入,得
解得
所以抛物线的解析式是.
设直线AB的解析式是,把A(3,0)B(0,)代入,得
解得
所以直线AB的解析式是.
(2)设点P的坐标是(),则M(,),因为在第四象限,所以PM=,当PM最长时,此时
==.
(3)若存在,则可能是:
①P在第四象限:平行四边形OBMP
,PM=OB=3,
PM最长时,所以不可能.
②P在第一象限平行四边形OBPM:
PM=OB=3,,解得,(舍去),所以P点的横坐标是.
③P在第三象限平行四边形OBPM:PM=OB=3,,解得(舍去),
①,所以P点的横坐标是.
所以P点的横坐标是或.
24.
解:(1)y=﹣x+3,令y=0,则x=3,令x=0,则y=3,
故点B、C的坐标为(3,0)、(0,3),
将点B、C的坐标代入y=x2+bx+c并解得:b=﹣4,
故抛物线的表达式为:y=x2﹣4x+3,
令y=0,则x=1或3,故点A(1,0),点P(2,﹣1);
(2)过点E作EH∥y轴交BC于点H,
设点E(x,x2﹣4x+3),则点H(x,﹣x+3)
S△CBE=HE×OB=×3×(﹣x+3﹣x2+4x﹣3)=(﹣x2+3x),
∵﹣<0,当x=时,S△CBE有最大值,
点E(,﹣);
(3)点C(0,3)、点P(2,﹣1),设点M(2,m),
CP2=4+16=20,CM2=4+(m﹣3)2=m2﹣6m+13,PM2=m2+2m+1,
①当CM=CP时,20=m2﹣6m+13,解得:m=7或﹣1(舍去m=﹣1);
②当CP=PM时,同理可得:m=﹣1±2;
③当CM=PM时,同理可得:m=;
故点M坐标为:(2,7)或(2,﹣1+2
=)或(2,﹣1﹣2)或(2,).
25.
(1)把x=0代入y=﹣x+3,得:y=3,
∴C(0,3).
把y=0代入y=﹣x+3得:x=3,
∴B(3,0),A(﹣1,0).
将C(0,3)、B(3,0)代入y=﹣x2+bx+c得:
,解得b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图所示:作点O关于BC的对称点O′,则O′(3,3).
∵O′与O关于BC对称,
∴PO=PO′.
∴OP+AP=O′P+AP≤AO′.
∴OP+AP的最小值=O′A==5.
O′A的方程为y=
P点满足解得:
所以P
(
,)
(3)y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
又∵C(0,3,B(3,0),
∴CD=,BC=3,DB=2.
∴CD2+CB2=BD2,
∴∠DCB=90°.
∵A(﹣1,0),C(0,3),
∴OA=1,CO=3.
∴.
又∵∠AOC=DCB=90°,
∴△AOC∽△DCB.
∴当Q的坐标为(0,0)时,△AQC∽△DCB.
如图所示:连接AC,过点C作CQ⊥AC,交x轴与点Q.
∵△ACQ为直角三角形,CO⊥AQ,
∴△ACQ∽△AOC.
又∵△AOC∽△DCB,
∴△ACQ∽△DCB.
∴,即,解得:AQ=10.
∴Q(9,0).
综上所述,当Q的坐标为(0,0)或(9,0)时,以A、C、Q为顶点的三角形与△BCD相似.
