华东师大版九年级数学下册 第26章 二次函数 单元测试题(word版含解析)
文档属性
| 名称 | 华东师大版九年级数学下册 第26章 二次函数 单元测试题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 132.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 08:44:29 | ||
图片预览


文档简介
1211580012052300123190000第26章 二次函数 单元测试题
(满分100分;时间:90分钟)
一、 选择题 (本题共计 7 小题 ,每题 3 分 ,共计21分 , )
?1. 下列函数中是二次函数的是( )
A.y=ax2+bx+c B.y=3x2+1 C.y=2(x+1)2-2x2 D.y=1x+x2
?
2. 已知二次函数的图象如右图,则下列结论中,正确的结论有( )
①a+b+c>0? ②a-b+c<0? ?③abc<0???④b=2a? ?⑤b>0.
A.5个 B.4个 C.3个 D.2个
?
3. 若正方形的边长为6,边长增加x,面积增加y,则y关于x的函数解析式为( )
A.y=(x+6)2 B.y=x2+62 C.y=x2+6x D.y=x2+12x
?
4. 已知二次函数y=a(x+1)2-b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a?
5. 二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,?1)和(-1,?0).下列结论:①ab<0;②b2>4ac;③0 A.1 B.2 C.3 D.4
?
6. 设函数y=a(x-h)2+k(a,h,k是实数,a≠0),当x=1时,y=1;当x=8时,y=8,( )
A.若h=4,则a<0 B.若h=5,则a>0
C.若h=6,则a<0 D.若h=7,则a>0
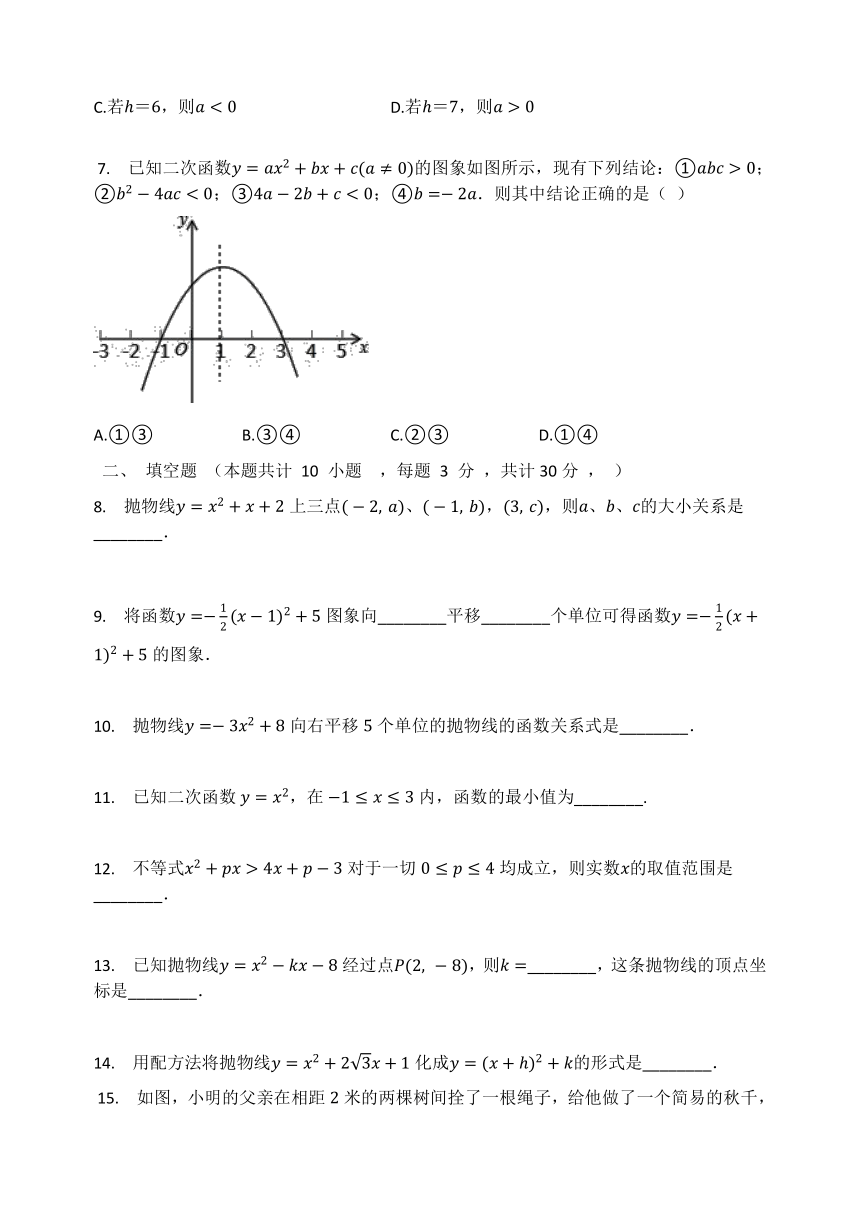
?7. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①abc>0;②b2-4ac<0;③4a-2b+c<0;④b=-2a.则其中结论正确的是( )
A.①③ B.③④ C.②③ D.①④
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
8. 抛物线y=x2+x+2上三点(-2,?a)、(-1,?b),(3,?c),则a、b、c的大小关系是________.
?
9. 将函数y=-12(x-1)2+5图象向________平移________个单位可得函数y=-12(x+1)2+5的图象.
?
10. 抛物线y=-3x2+8向右平移5个单位的抛物线的函数关系式是________.
?
11. 已知二次函数?y=x2,在?-1≤x≤3?内,函数的最小值为________.
?
12. 不等式x2+px>4x+p-3对于一切0≤p≤4均成立,则实数x的取值范围是________.
?
13. 已知抛物线y=x2-kx-8经过点P(2,?-8),则k=________,这条抛物线的顶点坐标是________.
?
14. 用配方法将抛物线y=x2+23x+1化成y=(x+h)2+k的形式是________.
?15. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为________米.
?16. 在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②-b2a>0;③abc>0;④a-b-c>0,说法正确的是________(填序号). ?
17. 如图,在平面直角坐标系中,抛物线y=-x2-4x+1与y轴交于点A,过点A平行于x轴的直线交抛物线y=x2于点B、C两点,点P在抛物线y=-x2-4x+1上且在x轴的上方,连接PB、PC,则△PBC面积的最大值是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
18. 已知抛物线y=x2-2x-3.
(1)直接写出抛物线的开口方向、对称轴和顶点坐标;
(2)若抛物线与x轴的两个交点为A、B,与y轴的一个交点为C,画草图,求△ABC的面积.
?
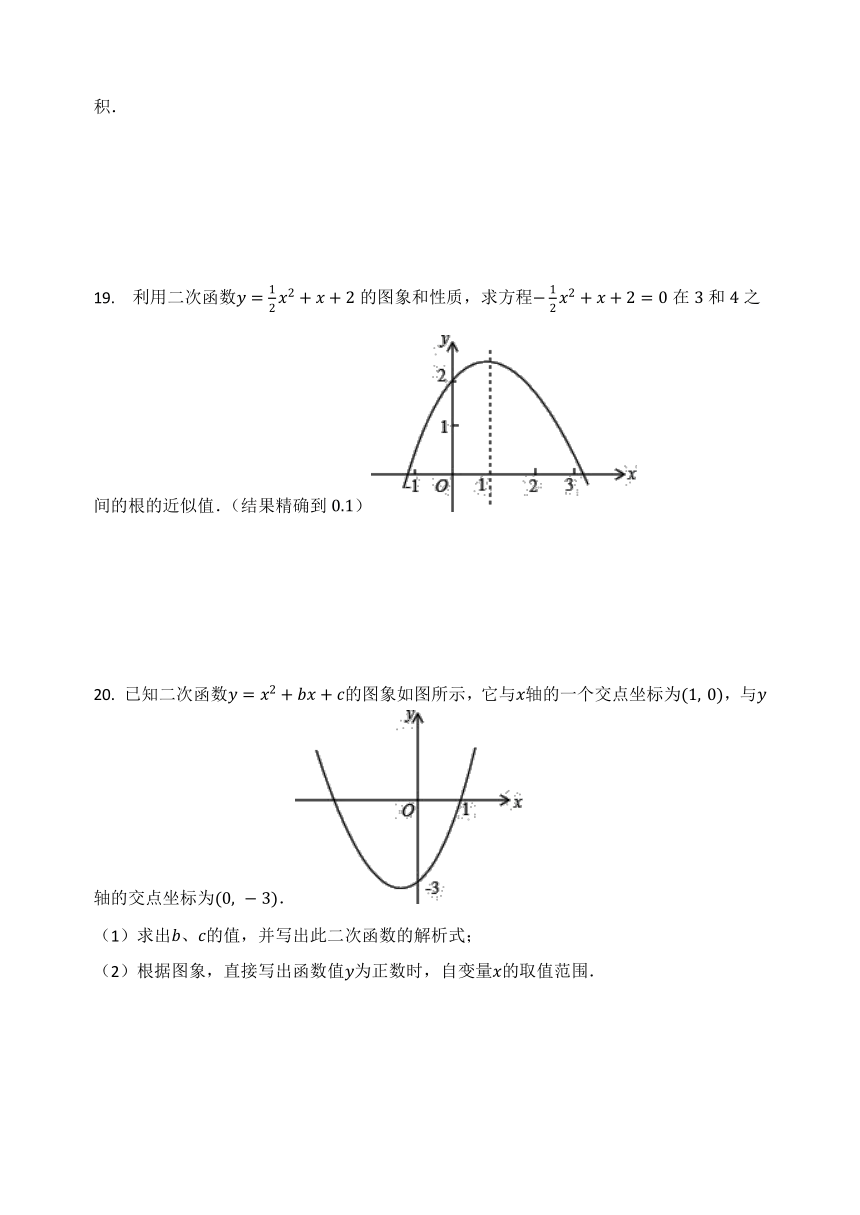
19. 利用二次函数y=12x2+x+2的图象和性质,求方程-12x2+x+2=0在3和4之间的根的近似值.(结果精确到0.1)
?
20. 已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(1,?0),与y轴的交点坐标为(0,?-3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围.
?
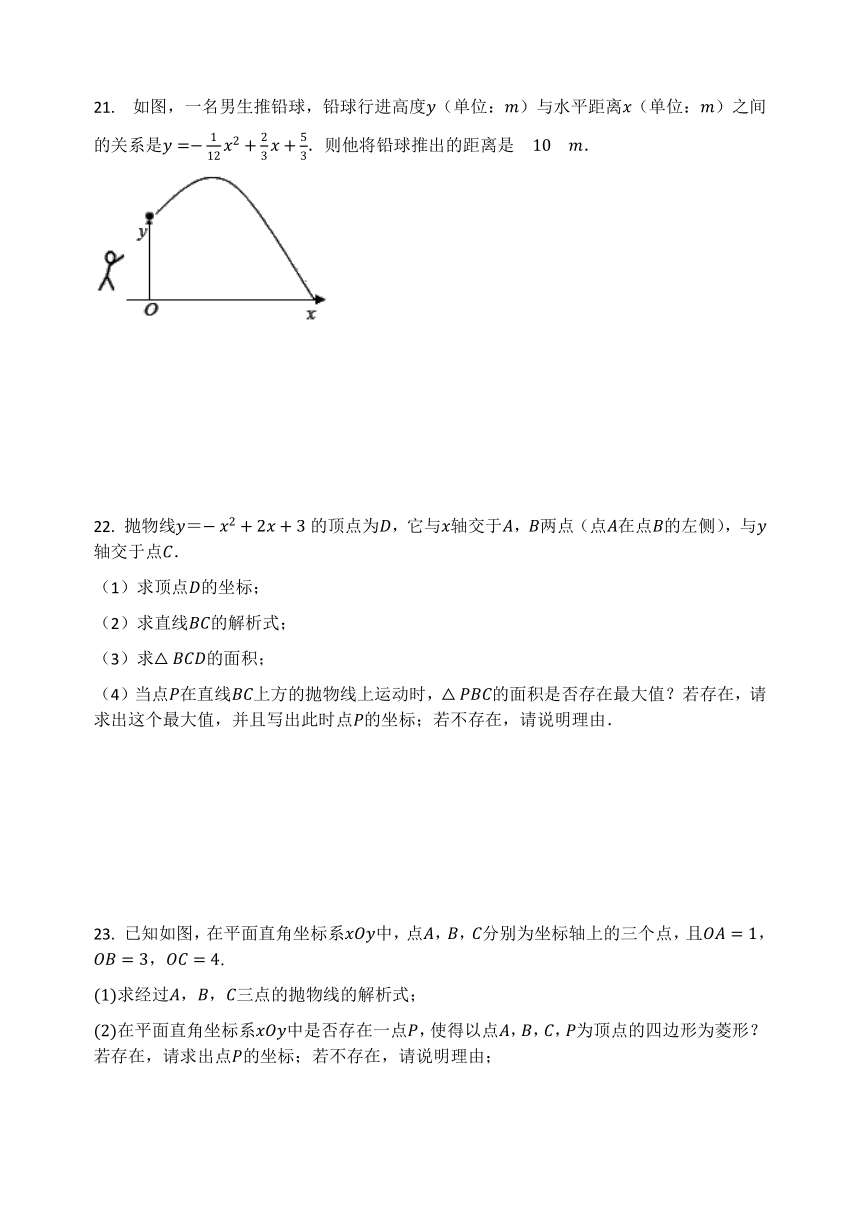
21. 如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-112x2+23x+53.则他将铅球推出的距离是 10 m.
?
22. 抛物线y=-x2+2x+3的顶点为D,它与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)求顶点D的坐标;
(2)求直线BC的解析式;
(3)求△BCD的面积;
(4)当点P在直线BC上方的抛物线上运动时,△PBC的面积是否存在最大值?若存在,请求出这个最大值,并且写出此时点P的坐标;若不存在,请说明理由.
?
23. 已知如图,在平面直角坐标系xOy中,点A,B,C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
(1)求经过A,B,C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以点A,B,C,P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出使|PM-AM|最大时点M的坐标,并直接写出|PM-AM|的最大值.
参考答案
一、 选择题 (本题共计 7 小题 ,每题 3 分 ,共计21分 )
1.
【答案】
B
【考点】
二次函数的定义
【解答】
解:A、y=ax2+bx+c,其中a≠0,故本选项错误;
B、y=3x2+1,故本选项正确;
C、y=2(x+1)2-2x2,整理后不含二次项,故本选项错误;
D、y=1x+x2,不是整式,故本选项错误;
故选B.
2.
【答案】
B
【考点】
二次函数图象与系数的关系
【解答】
解:根据图象,当x=1时,y=a+b+c>0,当x=-1时,y=a-b+c<0,可知①②正确;
根据图象与y轴的交点位置可知c>0,根据对称轴x=-b2a>0,且抛物线开口向下,a<0,
可知b>0,abc<0,故③⑤正确;
根据对称轴x=-b2a=1得b=-2a,可知④错误.
正确的是①②③⑤4个,故选B.
3.
【答案】
D
【考点】
根据实际问题列二次函数关系式
【解答】
解:原边长为6的正方形面积为:6×6=36,
边长增加x后边长变为:x+6,
则面积为:(x+6)2,
∴ y=(x+6)2-36=x2+12x.
故选:D.
4.
【答案】
A
【考点】
二次函数的最值
【解答】
解:∵ 二次函数y=a(x+1)2-b(a≠0)有最小值,
∴ 抛物线开口方向向上,即a>0;
又最小值为1,即-b=1,∴ b=-1,
∴ a>b.
故选A.
5.
【答案】
D
【考点】
二次函数图象上点的坐标特征
二次函数图象与系数的关系
抛物线与x轴的交点
【解答】
∵ 二次函数y=ax2+bx+c(a≠0)过点(0,?1)和(-1,?0),
∴ c=1,a-b+c=0.
①∵ 抛物线的对称轴在y轴右侧,∴ x=-b2a>0,
∴ a与b异号,∴ ab<0,正确;
②∵ 抛物线与x轴有两个不同的交点,∴ b2-4ac>0,
∴ b2>4ac,正确;
③∵ 抛物线开口向下,∴ a<0,
∵ ab<0,∴ b>0.
∵ a-b+c=0,c=1,∴ a=b-1,
∵ a<0,∴ b-1<0,b<1,
∴ 0④由图可知,当x<-1时,y<0,正确;
综上所述,正确的结论有①②③④.
6.
【答案】
C
【考点】
二次函数的性质
待定系数法求二次函数解析式
二次函数图象上点的坐标特征
【解答】
当x=1时,y=1;当x=8时,y=8;代入函数式得:,
∴ a(8-h)2-a(1-h)2=7,
整理得:a(9-2h)=1,
若h=4,则a=1,故A错误;
若h=5,则a=-1,故B错误;
若h=6,则a=-,故C正确;
若h=7,则a=-,故D错误;
7.
【答案】
B
【考点】
二次函数图象与系数的关系
【解答】
解:由抛物线的开口向下,得到a<0,
∵ -b2a>0,∴ b>0,
由抛物线与y轴交于正半轴,得到c>0,
∴ abc<0,选项①错误;
又抛物线与x轴有2个交点,∴ b2-4ac>0,选项②错误;
∵ x=-2时对应的函数值为负数,
∴ 4a-2b+c<0,选项③正确;
∵ 对称轴为直线x=1,∴ -b2a=1,即b=-2a,选项④正确,
则其中正确的选项有③④.
故选B
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
8.
【答案】
c>a>b
【考点】
二次函数图象上点的坐标特征
【解答】
解:∵ 二次函数的解析式为y=x2+x+2=(x+12)2+74,
∴ 抛物线的对称轴为直线x=-12,
∵ (-2,?a)、(-1,?b),(3,?c),
∴ 点(3,?c)离直线x=-12最远,(-1,?b)离真相x=-12最近,
而抛物线开口向上,
∴ c>a>b;
故答案为c>a>b.
9.
【答案】
左,2
【考点】
二次函数图象与几何变换
【解答】
解:由“左加右减”的原则将函数y=-12(x-1)2+5的图象向左平移2个单位,所得二次函数的解析式为:y=-12(x+1)2+5;
故答案为:左,2.
10.
【答案】
y=-3(x-5)2+8
【考点】
二次函数图象与几何变换
【解答】
解:∵ 抛物线y=-3x2+8顶点坐标为(0,?8),
向右平移5个单位后,顶点坐标为(5,?8),
由顶点式,得
平移后抛物线解析式为y=-3(x-5)2+8.
故本题答案为:y=-3(x-5)2+8.
11.
【答案】
0
【考点】
二次函数的最值
【解答】
解:y=x2的对称轴为x=0,且-1≤x≤3,
故x=0时,取最小值,最小值为0,
故答案为:0.
12.
【答案】
x<-1或x>3.
【考点】
二次函数与不等式(组)
【解答】
∵ x2+px>4x+p-3,
∴ x2-1>4x-px+p-4,
∴ x2-1>(4-p)x+p-4,
∴ x2-1>(4-p)(x-1),
当p=4时,x2-1>0,画出函数y=x2-1的图象,找出x轴上方所对应的x的取值范围得到x>1或x<-1;
当p=0时,x2-4x+3>0,画出函数y=x2-4x+3的图象,找出x轴上方所对应的x的取值范围得到x<1或x>3;
当0①当x>1,不等式变形为x+1>4-p>0,解得x>-1,则x>1;
②当x<1,不等式变形为x+1<4-p,则x+1<0,解得x<-1,则x<-1;
∴ x>1或x<-1;
综上所述,实数x的取值范围为x<-1或x>3.
13.
【答案】
2,(1,?-9)
【考点】
待定系数法求二次函数解析式
【解答】
解:∵ 抛物线y=x2-kx-8经过点P(2,?-8),
∴ 4-2k-8=-8,解得k=2,
∴ 此抛物线的解析式为y=x2-2x-8,
配方得y=(x-1)2-9,
∴ 这条抛物线的顶点坐标是(1,?-9).
14.
【答案】
y=(x+3)2-2
【考点】
二次函数的三种形式
【解答】
解:y=x2+23x+1=x2+23x+3-3+1=(x+3)2-2.
故化成y=(x+h)2+k的形式是y=(x+3)2-2.
15.
【答案】
0.5
【考点】
二次函数的应用
【解答】
解:以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,
由题意可得A(0,?2.5),B(2,?2.5),C(0.5,?1),
设函数解析式为y=ax2+bx+c,
把A,B,C三点分别代入得出c=2.5,
同时可得4a+2b+c=2.5,0.25a+0.5b+c=1,
解之得a=2,b=-4,c=2.5.
∴ y=2x2-4x+2.5=2(x-1)2+0.5.
∵ 2>0,
∴ 当x=1时,y=0.5米.
故答案为:0.5.
16.
【答案】
②③④
【考点】
二次函数图象与系数的关系
【解答】
解:由图可知,抛物线与x轴有2个交点,所以b2-4ac>0,故①错误;
对称轴在y轴右侧,则x=-b2a>0,故②正确;
抛物线开口向上,则a>0,
而对称轴在y轴右侧,则a、b异号,所以b<0,
其与y轴的交点(0,?c)位于y轴的负半轴,则c<0,
所以abc>0,故③正确;
∵ a>0,b<0,c<0,∴ a-b-c>0,故④正确;
故答案为:②③④.
17.
【答案】
4
【考点】
二次函数图象上点的坐标特征
抛物线与x轴的交点
【解答】
当x=0时,y=-x2-4x+1=1,则A(0,?1),
当y=1时,x2=1,解得x1=1,x2=-1,则B(-1,?1),C(1,?1),
∴ BC=2,
设P(x,?-x2-4x+1),
P点在BC上方时,△PBC面积有最大值,
∵ S△PBC=12?2?(-x2-4x+1-1)=-x2-4x=-(x+2)2+4,
∴ 当x=-2时,△PBC面积的最大值为4.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
18.
【答案】
解:(1)∵ y=x2-2x-3=(x-1)2-4,
∴ 该抛物线开口向上,对称轴为x=1,顶点坐标为(1,?-4).
(2)按点A在点B的左侧画出草图,如图所示.
∵ y=x2-2x-3=(x+1)(x-3),
∴ 点A(-1,?0),点B(3,?0),
当x=0时,y=-3,
∴ 点C(0,?-3),
∴ S△ABC=12AB?OC=12×[3-(-1)]×|-3|=6.
【考点】
抛物线与x轴的交点
【解答】
解:(1)∵ y=x2-2x-3=(x-1)2-4,
∴ 该抛物线开口向上,对称轴为x=1,顶点坐标为(1,?-4).
(2)按点A在点B的左侧画出草图,如图所示.
∵ y=x2-2x-3=(x+1)(x-3),
∴ 点A(-1,?0),点B(3,?0),
当x=0时,y=-3,
∴ 点C(0,?-3),
∴ S△ABC=12AB?OC=12×[3-(-1)]×|-3|=6.
19.
【答案】
解:方程-12x2+x+2=0根是函数y=12x2+x+2与x轴交点的横坐标.
如图所示:二次函数y=12x2+x+2的图象,
由图象可知方程有两个根,一个在-2和-1之间,另一个在3和4之间.
当x=3.2时,y=0.08;当x=3.3时,y=-0.145;
因此,x=3.2是方程的一个近似根,
故方程-12x2+x+2=0在3和4之间的根的近似值为x≈3.2.
【考点】
图象法求一元二次方程的近似根
【解答】
解:方程-12x2+x+2=0根是函数y=12x2+x+2与x轴交点的横坐标.
如图所示:二次函数y=12x2+x+2的图象,
由图象可知方程有两个根,一个在-2和-1之间,另一个在3和4之间.
当x=3.2时,y=0.08;当x=3.3时,y=-0.145;
因此,x=3.2是方程的一个近似根,
故方程-12x2+x+2=0在3和4之间的根的近似值为x≈3.2.
20.
【答案】
解:(1)由二次函数y=x2+bx+c的图象经过(1,?0)和(0,?-3)两点,
得1+b+c=0c=-3,
解这个方程组,得b=2c=-3;
∴ 抛物线的解析式为y=x2+2x-3.
(2)当x<-3或x>1时,y>0.
【考点】
待定系数法求二次函数解析式
二次函数与不等式(组)
【解答】
解:(1)由二次函数y=x2+bx+c的图象经过(1,?0)和(0,?-3)两点,
得1+b+c=0c=-3,
解这个方程组,得b=2c=-3;
∴ 抛物线的解析式为y=x2+2x-3.
(2)当x<-3或x>1时,y>0.
21.
【答案】
当y=0时,-112x2+23x+53=0,
解之得x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米.
【考点】
二次函数的应用
【解答】
当y=0时,-112x2+23x+53=0,
解之得x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米.
22.
【答案】
函数的对称轴为:x=1,
当x=1时,y=-1+2+3=4,
故点D(1,?4);
y=-x2+2x+3的顶点为D,它与x轴交于A,B两点,与y轴交于点C,
则点A、B、C的坐标分别为:(-1,?0)、(3,?0)、(0,?3),
将点B、C的坐标代入一次函数表达式:y=kx+b得:0=3k+bb=3?,解得:k=-1b=3?,
故直线BC的表达式为:y=-x+3;
过点D作DG?//?y轴交BC于点G,则点G(1,?2),
△BCD的面积=12×DG×OB=12×(4-2)×3=3;
过点P作y轴的平行线交BC于点H,
设点P(x,?-x2+2x+3),点H(x,?-x+3),
则S△PBC=12×PH×OB=32(-x2+2x+3+x-3)=-32x(x-3),
∵ -32<0,
∴ S△PBC有最大值,最大值为:278,
此时点P(32,?154).
【考点】
二次函数综合题
【解答】
函数的对称轴为:x=1,
当x=1时,y=-1+2+3=4,
故点D(1,?4);
y=-x2+2x+3的顶点为D,它与x轴交于A,B两点,与y轴交于点C,
则点A、B、C的坐标分别为:(-1,?0)、(3,?0)、(0,?3),
将点B、C的坐标代入一次函数表达式:y=kx+b得:0=3k+bb=3?,解得:k=-1b=3?,
故直线BC的表达式为:y=-x+3;
过点D作DG?//?y轴交BC于点G,则点G(1,?2),
△BCD的面积=12×DG×OB=12×(4-2)×3=3;
过点P作y轴的平行线交BC于点H,
设点P(x,?-x2+2x+3),点H(x,?-x+3),
则S△PBC=12×PH×OB=32(-x2+2x+3+x-3)=-32x(x-3),
∵ -32<0,
∴ S△PBC有最大值,最大值为:278,
此时点P(32,?154).
23.
【答案】
解:(1)设抛物线的解析式为y=ax2+bx+c.
由题意可知,A(1,?0),B(0,?3),C(-4,?0),
∴ a+b+c=0,c=3,16a-4b+c=0,?
解得:a=-34,b=-94,c=3,
∴ 经过A,B,C三点的抛物线的解析式为y=-34x2-94x+3.
(2)在平面直角坐标系xOy中存在一点P,
使得以点A,B,C,P为顶点的四边形为菱形,理由如下:
如图,
∵ OB=3,OC=4,OA=1,
∴ BC=AC=5.
当BP平行且等于AC时,四边形ACBP为菱形,
∴ BP=AC=5,且点P到x轴的距离等于OB,
∴ 点P的坐标为(5,?3).
当点P在第二、三象限时,以点A,B,C,P为顶点的四边形只能是平行四边形,不是菱形,
则当点P的坐标为(5,?3)时,以点A,B,C,P为顶点的四边形为菱形.
(3)设直线PA的解析式为y=kx+b(k≠0).
∵ A(1,?0),P(5,?3),
∴ 5k+b=3,k+b=0,?解得:k=34,b=-34,
∴ 直线PA的解析式为y=34x-34.
当点M与点P,A不在同一直线上时,
根据三角形的三边关系可得:|PM-AM|当点M与点P,A在同一直线上时,|PM-AM|=PA,
∴ 当点M与点P,A在同一直线上时,|PM-AM|的值最大,
即点M为直线PA与抛物线的交点,
解方程组y=34x-34,y=-34x2-94x+3,?得x1=1,y1=0?或x2=-5,y2=-92,?
∴ 当点M的坐标为(1,0)或(-5,?-92)时,|PM-AM|的值最大,
此时|PM-AM|的最大值为5.
【考点】
二次函数综合题
待定系数法求二次函数解析式
【解答】
解:(1)设抛物线的解析式为y=ax2+bx+c.
由题意可知,A(1,?0),B(0,?3),C(-4,?0),
∴ a+b+c=0,c=3,16a-4b+c=0,?
解得:a=-34,b=-94,c=3,
∴ 经过A,B,C三点的抛物线的解析式为y=-34x2-94x+3.
(2)在平面直角坐标系xOy中存在一点P,
使得以点A,B,C,P为顶点的四边形为菱形,理由如下:
如图,
∵ OB=3,OC=4,OA=1,
∴ BC=AC=5.
当BP平行且等于AC时,四边形ACBP为菱形,
∴ BP=AC=5,且点P到x轴的距离等于OB,
∴ 点P的坐标为(5,?3).
当点P在第二、三象限时,以点A,B,C,P为顶点的四边形只能是平行四边形,不是菱形,
则当点P的坐标为(5,?3)时,以点A,B,C,P为顶点的四边形为菱形.
(3)设直线PA的解析式为y=kx+b(k≠0).
∵ A(1,?0),P(5,?3),
∴ 5k+b=3,k+b=0,?解得:k=34,b=-34,
∴ 直线PA的解析式为y=34x-34.
当点M与点P,A不在同一直线上时,
根据三角形的三边关系可得:|PM-AM|当点M与点P,A在同一直线上时,|PM-AM|=PA,
∴ 当点M与点P,A在同一直线上时,|PM-AM|的值最大,
即点M为直线PA与抛物线的交点,
解方程组y=34x-34,y=-34x2-94x+3,?得x1=1,y1=0?或x2=-5,y2=-92,?
∴ 当点M的坐标为(1,0)或(-5,?-92)时,|PM-AM|的值最大,
此时|PM-AM|的最大值为5.
(满分100分;时间:90分钟)
一、 选择题 (本题共计 7 小题 ,每题 3 分 ,共计21分 , )
?1. 下列函数中是二次函数的是( )
A.y=ax2+bx+c B.y=3x2+1 C.y=2(x+1)2-2x2 D.y=1x+x2
?
2. 已知二次函数的图象如右图,则下列结论中,正确的结论有( )
①a+b+c>0? ②a-b+c<0? ?③abc<0???④b=2a? ?⑤b>0.
A.5个 B.4个 C.3个 D.2个
?
3. 若正方形的边长为6,边长增加x,面积增加y,则y关于x的函数解析式为( )
A.y=(x+6)2 B.y=x2+62 C.y=x2+6x D.y=x2+12x
?
4. 已知二次函数y=a(x+1)2-b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a?
5. 二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,?1)和(-1,?0).下列结论:①ab<0;②b2>4ac;③0
?
6. 设函数y=a(x-h)2+k(a,h,k是实数,a≠0),当x=1时,y=1;当x=8时,y=8,( )
A.若h=4,则a<0 B.若h=5,则a>0
C.若h=6,则a<0 D.若h=7,则a>0
?7. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①abc>0;②b2-4ac<0;③4a-2b+c<0;④b=-2a.则其中结论正确的是( )
A.①③ B.③④ C.②③ D.①④
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
8. 抛物线y=x2+x+2上三点(-2,?a)、(-1,?b),(3,?c),则a、b、c的大小关系是________.
?
9. 将函数y=-12(x-1)2+5图象向________平移________个单位可得函数y=-12(x+1)2+5的图象.
?
10. 抛物线y=-3x2+8向右平移5个单位的抛物线的函数关系式是________.
?
11. 已知二次函数?y=x2,在?-1≤x≤3?内,函数的最小值为________.
?
12. 不等式x2+px>4x+p-3对于一切0≤p≤4均成立,则实数x的取值范围是________.
?
13. 已知抛物线y=x2-kx-8经过点P(2,?-8),则k=________,这条抛物线的顶点坐标是________.
?
14. 用配方法将抛物线y=x2+23x+1化成y=(x+h)2+k的形式是________.
?15. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为________米.
?16. 在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②-b2a>0;③abc>0;④a-b-c>0,说法正确的是________(填序号). ?
17. 如图,在平面直角坐标系中,抛物线y=-x2-4x+1与y轴交于点A,过点A平行于x轴的直线交抛物线y=x2于点B、C两点,点P在抛物线y=-x2-4x+1上且在x轴的上方,连接PB、PC,则△PBC面积的最大值是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
18. 已知抛物线y=x2-2x-3.
(1)直接写出抛物线的开口方向、对称轴和顶点坐标;
(2)若抛物线与x轴的两个交点为A、B,与y轴的一个交点为C,画草图,求△ABC的面积.
?
19. 利用二次函数y=12x2+x+2的图象和性质,求方程-12x2+x+2=0在3和4之间的根的近似值.(结果精确到0.1)
?
20. 已知二次函数y=x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(1,?0),与y轴的交点坐标为(0,?-3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围.
?
21. 如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=-112x2+23x+53.则他将铅球推出的距离是 10 m.
?
22. 抛物线y=-x2+2x+3的顶点为D,它与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)求顶点D的坐标;
(2)求直线BC的解析式;
(3)求△BCD的面积;
(4)当点P在直线BC上方的抛物线上运动时,△PBC的面积是否存在最大值?若存在,请求出这个最大值,并且写出此时点P的坐标;若不存在,请说明理由.
?
23. 已知如图,在平面直角坐标系xOy中,点A,B,C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
(1)求经过A,B,C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以点A,B,C,P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出使|PM-AM|最大时点M的坐标,并直接写出|PM-AM|的最大值.
参考答案
一、 选择题 (本题共计 7 小题 ,每题 3 分 ,共计21分 )
1.
【答案】
B
【考点】
二次函数的定义
【解答】
解:A、y=ax2+bx+c,其中a≠0,故本选项错误;
B、y=3x2+1,故本选项正确;
C、y=2(x+1)2-2x2,整理后不含二次项,故本选项错误;
D、y=1x+x2,不是整式,故本选项错误;
故选B.
2.
【答案】
B
【考点】
二次函数图象与系数的关系
【解答】
解:根据图象,当x=1时,y=a+b+c>0,当x=-1时,y=a-b+c<0,可知①②正确;
根据图象与y轴的交点位置可知c>0,根据对称轴x=-b2a>0,且抛物线开口向下,a<0,
可知b>0,abc<0,故③⑤正确;
根据对称轴x=-b2a=1得b=-2a,可知④错误.
正确的是①②③⑤4个,故选B.
3.
【答案】
D
【考点】
根据实际问题列二次函数关系式
【解答】
解:原边长为6的正方形面积为:6×6=36,
边长增加x后边长变为:x+6,
则面积为:(x+6)2,
∴ y=(x+6)2-36=x2+12x.
故选:D.
4.
【答案】
A
【考点】
二次函数的最值
【解答】
解:∵ 二次函数y=a(x+1)2-b(a≠0)有最小值,
∴ 抛物线开口方向向上,即a>0;
又最小值为1,即-b=1,∴ b=-1,
∴ a>b.
故选A.
5.
【答案】
D
【考点】
二次函数图象上点的坐标特征
二次函数图象与系数的关系
抛物线与x轴的交点
【解答】
∵ 二次函数y=ax2+bx+c(a≠0)过点(0,?1)和(-1,?0),
∴ c=1,a-b+c=0.
①∵ 抛物线的对称轴在y轴右侧,∴ x=-b2a>0,
∴ a与b异号,∴ ab<0,正确;
②∵ 抛物线与x轴有两个不同的交点,∴ b2-4ac>0,
∴ b2>4ac,正确;
③∵ 抛物线开口向下,∴ a<0,
∵ ab<0,∴ b>0.
∵ a-b+c=0,c=1,∴ a=b-1,
∵ a<0,∴ b-1<0,b<1,
∴ 0
综上所述,正确的结论有①②③④.
6.
【答案】
C
【考点】
二次函数的性质
待定系数法求二次函数解析式
二次函数图象上点的坐标特征
【解答】
当x=1时,y=1;当x=8时,y=8;代入函数式得:,
∴ a(8-h)2-a(1-h)2=7,
整理得:a(9-2h)=1,
若h=4,则a=1,故A错误;
若h=5,则a=-1,故B错误;
若h=6,则a=-,故C正确;
若h=7,则a=-,故D错误;
7.
【答案】
B
【考点】
二次函数图象与系数的关系
【解答】
解:由抛物线的开口向下,得到a<0,
∵ -b2a>0,∴ b>0,
由抛物线与y轴交于正半轴,得到c>0,
∴ abc<0,选项①错误;
又抛物线与x轴有2个交点,∴ b2-4ac>0,选项②错误;
∵ x=-2时对应的函数值为负数,
∴ 4a-2b+c<0,选项③正确;
∵ 对称轴为直线x=1,∴ -b2a=1,即b=-2a,选项④正确,
则其中正确的选项有③④.
故选B
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
8.
【答案】
c>a>b
【考点】
二次函数图象上点的坐标特征
【解答】
解:∵ 二次函数的解析式为y=x2+x+2=(x+12)2+74,
∴ 抛物线的对称轴为直线x=-12,
∵ (-2,?a)、(-1,?b),(3,?c),
∴ 点(3,?c)离直线x=-12最远,(-1,?b)离真相x=-12最近,
而抛物线开口向上,
∴ c>a>b;
故答案为c>a>b.
9.
【答案】
左,2
【考点】
二次函数图象与几何变换
【解答】
解:由“左加右减”的原则将函数y=-12(x-1)2+5的图象向左平移2个单位,所得二次函数的解析式为:y=-12(x+1)2+5;
故答案为:左,2.
10.
【答案】
y=-3(x-5)2+8
【考点】
二次函数图象与几何变换
【解答】
解:∵ 抛物线y=-3x2+8顶点坐标为(0,?8),
向右平移5个单位后,顶点坐标为(5,?8),
由顶点式,得
平移后抛物线解析式为y=-3(x-5)2+8.
故本题答案为:y=-3(x-5)2+8.
11.
【答案】
0
【考点】
二次函数的最值
【解答】
解:y=x2的对称轴为x=0,且-1≤x≤3,
故x=0时,取最小值,最小值为0,
故答案为:0.
12.
【答案】
x<-1或x>3.
【考点】
二次函数与不等式(组)
【解答】
∵ x2+px>4x+p-3,
∴ x2-1>4x-px+p-4,
∴ x2-1>(4-p)x+p-4,
∴ x2-1>(4-p)(x-1),
当p=4时,x2-1>0,画出函数y=x2-1的图象,找出x轴上方所对应的x的取值范围得到x>1或x<-1;
当p=0时,x2-4x+3>0,画出函数y=x2-4x+3的图象,找出x轴上方所对应的x的取值范围得到x<1或x>3;
当0
②当x<1,不等式变形为x+1<4-p,则x+1<0,解得x<-1,则x<-1;
∴ x>1或x<-1;
综上所述,实数x的取值范围为x<-1或x>3.
13.
【答案】
2,(1,?-9)
【考点】
待定系数法求二次函数解析式
【解答】
解:∵ 抛物线y=x2-kx-8经过点P(2,?-8),
∴ 4-2k-8=-8,解得k=2,
∴ 此抛物线的解析式为y=x2-2x-8,
配方得y=(x-1)2-9,
∴ 这条抛物线的顶点坐标是(1,?-9).
14.
【答案】
y=(x+3)2-2
【考点】
二次函数的三种形式
【解答】
解:y=x2+23x+1=x2+23x+3-3+1=(x+3)2-2.
故化成y=(x+h)2+k的形式是y=(x+3)2-2.
15.
【答案】
0.5
【考点】
二次函数的应用
【解答】
解:以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,
由题意可得A(0,?2.5),B(2,?2.5),C(0.5,?1),
设函数解析式为y=ax2+bx+c,
把A,B,C三点分别代入得出c=2.5,
同时可得4a+2b+c=2.5,0.25a+0.5b+c=1,
解之得a=2,b=-4,c=2.5.
∴ y=2x2-4x+2.5=2(x-1)2+0.5.
∵ 2>0,
∴ 当x=1时,y=0.5米.
故答案为:0.5.
16.
【答案】
②③④
【考点】
二次函数图象与系数的关系
【解答】
解:由图可知,抛物线与x轴有2个交点,所以b2-4ac>0,故①错误;
对称轴在y轴右侧,则x=-b2a>0,故②正确;
抛物线开口向上,则a>0,
而对称轴在y轴右侧,则a、b异号,所以b<0,
其与y轴的交点(0,?c)位于y轴的负半轴,则c<0,
所以abc>0,故③正确;
∵ a>0,b<0,c<0,∴ a-b-c>0,故④正确;
故答案为:②③④.
17.
【答案】
4
【考点】
二次函数图象上点的坐标特征
抛物线与x轴的交点
【解答】
当x=0时,y=-x2-4x+1=1,则A(0,?1),
当y=1时,x2=1,解得x1=1,x2=-1,则B(-1,?1),C(1,?1),
∴ BC=2,
设P(x,?-x2-4x+1),
P点在BC上方时,△PBC面积有最大值,
∵ S△PBC=12?2?(-x2-4x+1-1)=-x2-4x=-(x+2)2+4,
∴ 当x=-2时,△PBC面积的最大值为4.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
18.
【答案】
解:(1)∵ y=x2-2x-3=(x-1)2-4,
∴ 该抛物线开口向上,对称轴为x=1,顶点坐标为(1,?-4).
(2)按点A在点B的左侧画出草图,如图所示.
∵ y=x2-2x-3=(x+1)(x-3),
∴ 点A(-1,?0),点B(3,?0),
当x=0时,y=-3,
∴ 点C(0,?-3),
∴ S△ABC=12AB?OC=12×[3-(-1)]×|-3|=6.
【考点】
抛物线与x轴的交点
【解答】
解:(1)∵ y=x2-2x-3=(x-1)2-4,
∴ 该抛物线开口向上,对称轴为x=1,顶点坐标为(1,?-4).
(2)按点A在点B的左侧画出草图,如图所示.
∵ y=x2-2x-3=(x+1)(x-3),
∴ 点A(-1,?0),点B(3,?0),
当x=0时,y=-3,
∴ 点C(0,?-3),
∴ S△ABC=12AB?OC=12×[3-(-1)]×|-3|=6.
19.
【答案】
解:方程-12x2+x+2=0根是函数y=12x2+x+2与x轴交点的横坐标.
如图所示:二次函数y=12x2+x+2的图象,
由图象可知方程有两个根,一个在-2和-1之间,另一个在3和4之间.
当x=3.2时,y=0.08;当x=3.3时,y=-0.145;
因此,x=3.2是方程的一个近似根,
故方程-12x2+x+2=0在3和4之间的根的近似值为x≈3.2.
【考点】
图象法求一元二次方程的近似根
【解答】
解:方程-12x2+x+2=0根是函数y=12x2+x+2与x轴交点的横坐标.
如图所示:二次函数y=12x2+x+2的图象,
由图象可知方程有两个根,一个在-2和-1之间,另一个在3和4之间.
当x=3.2时,y=0.08;当x=3.3时,y=-0.145;
因此,x=3.2是方程的一个近似根,
故方程-12x2+x+2=0在3和4之间的根的近似值为x≈3.2.
20.
【答案】
解:(1)由二次函数y=x2+bx+c的图象经过(1,?0)和(0,?-3)两点,
得1+b+c=0c=-3,
解这个方程组,得b=2c=-3;
∴ 抛物线的解析式为y=x2+2x-3.
(2)当x<-3或x>1时,y>0.
【考点】
待定系数法求二次函数解析式
二次函数与不等式(组)
【解答】
解:(1)由二次函数y=x2+bx+c的图象经过(1,?0)和(0,?-3)两点,
得1+b+c=0c=-3,
解这个方程组,得b=2c=-3;
∴ 抛物线的解析式为y=x2+2x-3.
(2)当x<-3或x>1时,y>0.
21.
【答案】
当y=0时,-112x2+23x+53=0,
解之得x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米.
【考点】
二次函数的应用
【解答】
当y=0时,-112x2+23x+53=0,
解之得x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米.
22.
【答案】
函数的对称轴为:x=1,
当x=1时,y=-1+2+3=4,
故点D(1,?4);
y=-x2+2x+3的顶点为D,它与x轴交于A,B两点,与y轴交于点C,
则点A、B、C的坐标分别为:(-1,?0)、(3,?0)、(0,?3),
将点B、C的坐标代入一次函数表达式:y=kx+b得:0=3k+bb=3?,解得:k=-1b=3?,
故直线BC的表达式为:y=-x+3;
过点D作DG?//?y轴交BC于点G,则点G(1,?2),
△BCD的面积=12×DG×OB=12×(4-2)×3=3;
过点P作y轴的平行线交BC于点H,
设点P(x,?-x2+2x+3),点H(x,?-x+3),
则S△PBC=12×PH×OB=32(-x2+2x+3+x-3)=-32x(x-3),
∵ -32<0,
∴ S△PBC有最大值,最大值为:278,
此时点P(32,?154).
【考点】
二次函数综合题
【解答】
函数的对称轴为:x=1,
当x=1时,y=-1+2+3=4,
故点D(1,?4);
y=-x2+2x+3的顶点为D,它与x轴交于A,B两点,与y轴交于点C,
则点A、B、C的坐标分别为:(-1,?0)、(3,?0)、(0,?3),
将点B、C的坐标代入一次函数表达式:y=kx+b得:0=3k+bb=3?,解得:k=-1b=3?,
故直线BC的表达式为:y=-x+3;
过点D作DG?//?y轴交BC于点G,则点G(1,?2),
△BCD的面积=12×DG×OB=12×(4-2)×3=3;
过点P作y轴的平行线交BC于点H,
设点P(x,?-x2+2x+3),点H(x,?-x+3),
则S△PBC=12×PH×OB=32(-x2+2x+3+x-3)=-32x(x-3),
∵ -32<0,
∴ S△PBC有最大值,最大值为:278,
此时点P(32,?154).
23.
【答案】
解:(1)设抛物线的解析式为y=ax2+bx+c.
由题意可知,A(1,?0),B(0,?3),C(-4,?0),
∴ a+b+c=0,c=3,16a-4b+c=0,?
解得:a=-34,b=-94,c=3,
∴ 经过A,B,C三点的抛物线的解析式为y=-34x2-94x+3.
(2)在平面直角坐标系xOy中存在一点P,
使得以点A,B,C,P为顶点的四边形为菱形,理由如下:
如图,
∵ OB=3,OC=4,OA=1,
∴ BC=AC=5.
当BP平行且等于AC时,四边形ACBP为菱形,
∴ BP=AC=5,且点P到x轴的距离等于OB,
∴ 点P的坐标为(5,?3).
当点P在第二、三象限时,以点A,B,C,P为顶点的四边形只能是平行四边形,不是菱形,
则当点P的坐标为(5,?3)时,以点A,B,C,P为顶点的四边形为菱形.
(3)设直线PA的解析式为y=kx+b(k≠0).
∵ A(1,?0),P(5,?3),
∴ 5k+b=3,k+b=0,?解得:k=34,b=-34,
∴ 直线PA的解析式为y=34x-34.
当点M与点P,A不在同一直线上时,
根据三角形的三边关系可得:|PM-AM|
∴ 当点M与点P,A在同一直线上时,|PM-AM|的值最大,
即点M为直线PA与抛物线的交点,
解方程组y=34x-34,y=-34x2-94x+3,?得x1=1,y1=0?或x2=-5,y2=-92,?
∴ 当点M的坐标为(1,0)或(-5,?-92)时,|PM-AM|的值最大,
此时|PM-AM|的最大值为5.
【考点】
二次函数综合题
待定系数法求二次函数解析式
【解答】
解:(1)设抛物线的解析式为y=ax2+bx+c.
由题意可知,A(1,?0),B(0,?3),C(-4,?0),
∴ a+b+c=0,c=3,16a-4b+c=0,?
解得:a=-34,b=-94,c=3,
∴ 经过A,B,C三点的抛物线的解析式为y=-34x2-94x+3.
(2)在平面直角坐标系xOy中存在一点P,
使得以点A,B,C,P为顶点的四边形为菱形,理由如下:
如图,
∵ OB=3,OC=4,OA=1,
∴ BC=AC=5.
当BP平行且等于AC时,四边形ACBP为菱形,
∴ BP=AC=5,且点P到x轴的距离等于OB,
∴ 点P的坐标为(5,?3).
当点P在第二、三象限时,以点A,B,C,P为顶点的四边形只能是平行四边形,不是菱形,
则当点P的坐标为(5,?3)时,以点A,B,C,P为顶点的四边形为菱形.
(3)设直线PA的解析式为y=kx+b(k≠0).
∵ A(1,?0),P(5,?3),
∴ 5k+b=3,k+b=0,?解得:k=34,b=-34,
∴ 直线PA的解析式为y=34x-34.
当点M与点P,A不在同一直线上时,
根据三角形的三边关系可得:|PM-AM|
∴ 当点M与点P,A在同一直线上时,|PM-AM|的值最大,
即点M为直线PA与抛物线的交点,
解方程组y=34x-34,y=-34x2-94x+3,?得x1=1,y1=0?或x2=-5,y2=-92,?
∴ 当点M的坐标为(1,0)或(-5,?-92)时,|PM-AM|的值最大,
此时|PM-AM|的最大值为5.
