华东师大版九年级下册数学 第27章 圆 27.2.1点与圆的位置关系 同步习题(word版含解析)
文档属性
| 名称 | 华东师大版九年级下册数学 第27章 圆 27.2.1点与圆的位置关系 同步习题(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 00:47:12 | ||
图片预览



文档简介
27.2.1点与圆的位置关系 同步习题
一.选择题
1.直角坐标系的原点为O,⊙O半径为5,点P(4,﹣3)( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.无法确定
2.⊙O的直径为10cm,圆心O到点A的距离为6cm,则点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上 C.点A在⊙O内 D.无法确定
3.已知⊙O的半径为6,点A与圆心O的距离为5,则点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O内
C.点A不在⊙O内 D.点A在⊙O上
4.若⊙O的半径是5cm,点A在⊙O内,则OA的长可能是( )
A.2cm B.5cm C.6cm D.10cm
5.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm B.大于3cm C.小于3cm D.等于3cm
6.在数轴上,点A所表示实数为5,点B所表示实数为a,⊙A半径为3.下列说法中不正确的是( )
A.当a>8时,点B在⊙A外 B.当a<8时,点B在⊙A内
C.当a<2时,点B在⊙A外 D.当2<a<8时,点B在⊙A内
7.已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O外 C.在⊙O上 D.无法确定
8.已知△ABC,以AB为直径作⊙O,∠C=88°,则点C在( )
A.⊙O上 B.⊙O外 C.⊙O 内 D.无法确定
9.如图,在直角坐标系中,⊙A的半径为2,圆心坐标为(4,0),y轴上有点B(0,3),点C是⊙A上的动点,点P是BC的中点,则OP的范围是( )
A.≤OP≤ B.2≤OP≤4 C.≤OP≤ D.3≤OP≤4
10.已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A. B. C. D.
二.填空题
11.在坐标系中,以O为圆心,5为半径的⊙O与点P(﹣4,4)的位置关系是:点P在⊙O (填“内”、“上”或“外”).
12.已知⊙O的直径为8,点P到圆心O的距离为5,则点P与⊙O的位置关系是 .
13.如图,在Rt△ABC中,∠ABC=90°,AB=12,BC=5,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的取值范围是 .
14.在平面直角坐标系中,已知A(﹣1,﹣1)、B(0,2)、C(3,3)都在⊙M上,则圆心M的坐标为 .
15.已知点C在线段AB上,且0<AC<AB.如果⊙C经过点A,那么点B与⊙C的位置关系是 .
三.解答题
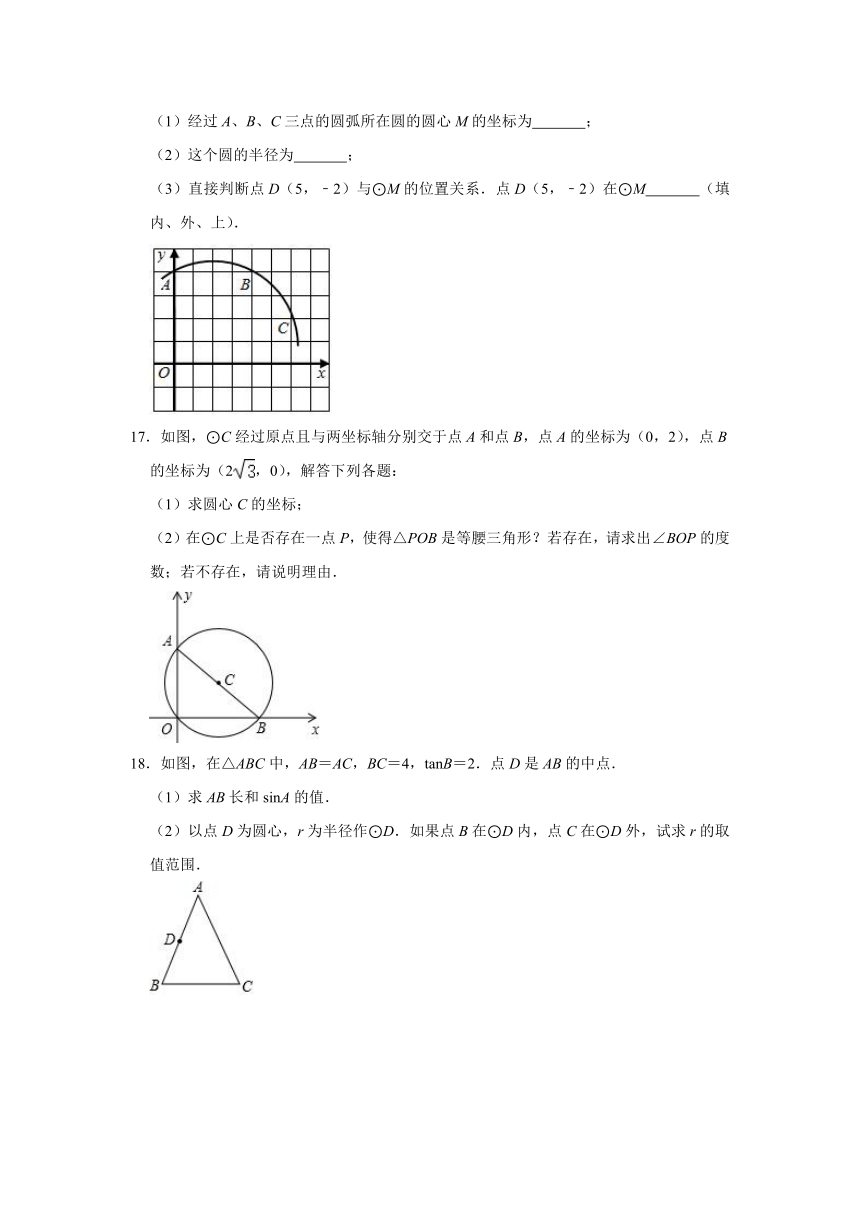
16.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为 ;
(2)这个圆的半径为 ;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M (填内、外、上).
17.如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),点B的坐标为(2,0),解答下列各题:
(1)求圆心C的坐标;
(2)在⊙C上是否存在一点P,使得△POB是等腰三角形?若存在,请求出∠BOP的度数;若不存在,请说明理由.
18.如图,在△ABC中,AB=AC,BC=4,tanB=2.点D是AB的中点.
(1)求AB长和sinA的值.
(2)以点D为圆心,r为半径作⊙D.如果点B在⊙D内,点C在⊙D外,试求r的取值范围.
参考答案
一.选择题
1.解:∵圆心P的坐标为(4,﹣3),
∴OP==5.
∵⊙O的半径为5,
∴点P在⊙O上.
故选:B.
2.】解:∵⊙O的直径为10cm,
∴⊙O的半径为5cm
∵点A到圆心O的距离为6cm,
即点A到圆心O的距离大于圆的半径,
∴点A在⊙O外.
故选:A.
3.解:∵OA<R,
∴点A在圆内,
故选:B.
4.解:∵点A在⊙O内,且⊙O的半径是5cm,
∴OA<5cm,
观察选项,只有选项A符合题意.
故选:A.
5.解:点P在⊙O外且⊙O的半径为3cm,
可知点P到圆心的距离大于r,即PO大于3,
故选:B.
6.解:如图,观察图象可知,当a>8时,点B在⊙A外,当a=2或8时,点B在⊙A上,当a<2或a>8时,点B在⊙A 外.
故选项A,C,D正确,
故选:B.
7.解:∵a=1,b=﹣2d,c=1,
∴△=b2﹣4ac=(﹣2d)2﹣4×1×1=4d2﹣4=0,
解得:d=1.
则点A在⊙O上.
故选:C.
8.解:如图,设⊙O交直线BC于D,连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠C=88°,
∴点C在⊙O外,
故选:B.
9.解:如图,在y轴上取点B'(0,﹣3),连接B'C,B'A,
∵点B(0,3),B'(0,﹣3),点A(4,0),
∴OB=OB'=3,OA=4,
∴B'A===5,
∵点P是BC的中点,
∴BP=PC,
∵OB=OB',BP=PC,
∴B'C=2OP,
当点C在线段B'A上时,B'C的长度最小值=5﹣2=3,
当点C在线段B'A的延长线上时,B'C的长度最大值=5+2=7,
∴≤OP≤,
故选:A.
10.解:解方程组得,
∴P点坐标为(3a﹣1,4a+2),
设x=3a﹣1,y=4a+2,
∴y=x+,
即点P为直线y=x+上一动点,
设直线y=x+与坐标的交点为A、B,如图,则A(﹣,0),B(0,),
∴AB==,
过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,
∵∠MBP=∠ABO,
∴Rt△MBP∽Rt△ABO,
∴MP:OA=BM:AB,即MP:=:,
∴MP=,
∴PQ=﹣1=,
即线段PQ的最小值为.
故选:C.
二.填空题
11.解:∵点P(﹣4,4),
∴OP==4,
∴OP大于圆的半径5,
∴点P在⊙O外,
故答案为:外.
12.解:根据题意,得
该圆的半径是4,小于点P到圆心O的距离5,则点P在⊙O外部,
故答案为在圆外.
13.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=12,BC=5,
∴AC=13,
∵AN=NC,
∴BN=AC=6.5,
∵AN=NC,DM=MC,
∴MN=AD=2,
∴BN﹣MN≤BM≤BN+NM,
∴6.5﹣2≤BM≤6.5+2,即4.5≤BM≤8.5,
故答案为:4.5≤BM≤8.5.
14.解:设M点的坐标为(x,y),由题意知,MA=MB=MC,
∴,
化简得,x+y=﹣3x﹣3y+8=﹣2y+1,
即,
解得,
∴M.
故答案为:.
15.解:如图,
∵点C在线段AB上,且0<AC<AB,
∴BC>AC,
∴点B在⊙C外,
故答案为:点B在⊙C外.
三.解答题
16.解:(1)如图,圆心M的坐标为(2,0);
(2)∵A(0,4),M(2,0),
∴MA==2,
即⊙M的半径为2;
(3)∵D(5,﹣2),M(2,0),
∴DM==,
∵<2,
∴点D在⊙M内.
故答案为(2,0);2;内.
17.解:(1)∵A(0,2),B(2,0)
∴OA=2,OB=2;
Rt△OAB中,由勾股定理,得:AB==4;
∵∠AOB=90°,
∴AB是⊙C的直径;
∴⊙C的半径r=2;
过C作CE⊥y轴于E,则CE∥OB;
∵C是AB的中点,
∴CE是△AOB的中位线,
则OE=OA=1,CE=OB=,即C(,1);
故⊙C的半径为2,C(,1);
(2)如图,作OB的垂直平分线,交⊙C于P1、P2,交OB于D,连接OC;
由垂径定理知:P1P2必过点C,即P1P2是⊙C的直径;
∴P1(,3),P2(,﹣1);
在Rt△ODP1中,P1D=3,OD=,
∴∠BOP1=60°;
∵P1P2是直径,
∴∠P1OP2=90°,∠BOP2=30°;
由于P1P2垂直平分OB,所以△OBP1、△OBP2都是等腰三角形,因此P1、P2均符合P点的要求;
由于此时同时BO=P1O,因此不需要考虑BO为腰的情况.
故存在符合条件的P点:P1(,3),∠BOP1=60°;P2(,﹣1),∠BOP2=30°.
18.解:(1)如图,过点A作AE⊥BC于点E.
∵AB=AC,BC=4,
∴
∵,
∴AE=4,
∴
又
∴.
(2)如图,连结CD,过点D作DF⊥BC于点F,显然DF∥AE
∵点D是AB中点,即DF是中位线
∴,
∴CF=3
∴
又
∴r的取值范围是
一.选择题
1.直角坐标系的原点为O,⊙O半径为5,点P(4,﹣3)( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.无法确定
2.⊙O的直径为10cm,圆心O到点A的距离为6cm,则点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上 C.点A在⊙O内 D.无法确定
3.已知⊙O的半径为6,点A与圆心O的距离为5,则点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O内
C.点A不在⊙O内 D.点A在⊙O上
4.若⊙O的半径是5cm,点A在⊙O内,则OA的长可能是( )
A.2cm B.5cm C.6cm D.10cm
5.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm B.大于3cm C.小于3cm D.等于3cm
6.在数轴上,点A所表示实数为5,点B所表示实数为a,⊙A半径为3.下列说法中不正确的是( )
A.当a>8时,点B在⊙A外 B.当a<8时,点B在⊙A内
C.当a<2时,点B在⊙A外 D.当2<a<8时,点B在⊙A内
7.已知⊙O的半径为1,AO=d,且关于x的方程x2﹣2dx+1=0有两个相等的实数根,则点A与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O外 C.在⊙O上 D.无法确定
8.已知△ABC,以AB为直径作⊙O,∠C=88°,则点C在( )
A.⊙O上 B.⊙O外 C.⊙O 内 D.无法确定
9.如图,在直角坐标系中,⊙A的半径为2,圆心坐标为(4,0),y轴上有点B(0,3),点C是⊙A上的动点,点P是BC的中点,则OP的范围是( )
A.≤OP≤ B.2≤OP≤4 C.≤OP≤ D.3≤OP≤4
10.已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A. B. C. D.
二.填空题
11.在坐标系中,以O为圆心,5为半径的⊙O与点P(﹣4,4)的位置关系是:点P在⊙O (填“内”、“上”或“外”).
12.已知⊙O的直径为8,点P到圆心O的距离为5,则点P与⊙O的位置关系是 .
13.如图,在Rt△ABC中,∠ABC=90°,AB=12,BC=5,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的取值范围是 .
14.在平面直角坐标系中,已知A(﹣1,﹣1)、B(0,2)、C(3,3)都在⊙M上,则圆心M的坐标为 .
15.已知点C在线段AB上,且0<AC<AB.如果⊙C经过点A,那么点B与⊙C的位置关系是 .
三.解答题
16.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为 ;
(2)这个圆的半径为 ;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M (填内、外、上).
17.如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),点B的坐标为(2,0),解答下列各题:
(1)求圆心C的坐标;
(2)在⊙C上是否存在一点P,使得△POB是等腰三角形?若存在,请求出∠BOP的度数;若不存在,请说明理由.
18.如图,在△ABC中,AB=AC,BC=4,tanB=2.点D是AB的中点.
(1)求AB长和sinA的值.
(2)以点D为圆心,r为半径作⊙D.如果点B在⊙D内,点C在⊙D外,试求r的取值范围.
参考答案
一.选择题
1.解:∵圆心P的坐标为(4,﹣3),
∴OP==5.
∵⊙O的半径为5,
∴点P在⊙O上.
故选:B.
2.】解:∵⊙O的直径为10cm,
∴⊙O的半径为5cm
∵点A到圆心O的距离为6cm,
即点A到圆心O的距离大于圆的半径,
∴点A在⊙O外.
故选:A.
3.解:∵OA<R,
∴点A在圆内,
故选:B.
4.解:∵点A在⊙O内,且⊙O的半径是5cm,
∴OA<5cm,
观察选项,只有选项A符合题意.
故选:A.
5.解:点P在⊙O外且⊙O的半径为3cm,
可知点P到圆心的距离大于r,即PO大于3,
故选:B.
6.解:如图,观察图象可知,当a>8时,点B在⊙A外,当a=2或8时,点B在⊙A上,当a<2或a>8时,点B在⊙A 外.
故选项A,C,D正确,
故选:B.
7.解:∵a=1,b=﹣2d,c=1,
∴△=b2﹣4ac=(﹣2d)2﹣4×1×1=4d2﹣4=0,
解得:d=1.
则点A在⊙O上.
故选:C.
8.解:如图,设⊙O交直线BC于D,连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠C=88°,
∴点C在⊙O外,
故选:B.
9.解:如图,在y轴上取点B'(0,﹣3),连接B'C,B'A,
∵点B(0,3),B'(0,﹣3),点A(4,0),
∴OB=OB'=3,OA=4,
∴B'A===5,
∵点P是BC的中点,
∴BP=PC,
∵OB=OB',BP=PC,
∴B'C=2OP,
当点C在线段B'A上时,B'C的长度最小值=5﹣2=3,
当点C在线段B'A的延长线上时,B'C的长度最大值=5+2=7,
∴≤OP≤,
故选:A.
10.解:解方程组得,
∴P点坐标为(3a﹣1,4a+2),
设x=3a﹣1,y=4a+2,
∴y=x+,
即点P为直线y=x+上一动点,
设直线y=x+与坐标的交点为A、B,如图,则A(﹣,0),B(0,),
∴AB==,
过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,
∵∠MBP=∠ABO,
∴Rt△MBP∽Rt△ABO,
∴MP:OA=BM:AB,即MP:=:,
∴MP=,
∴PQ=﹣1=,
即线段PQ的最小值为.
故选:C.
二.填空题
11.解:∵点P(﹣4,4),
∴OP==4,
∴OP大于圆的半径5,
∴点P在⊙O外,
故答案为:外.
12.解:根据题意,得
该圆的半径是4,小于点P到圆心O的距离5,则点P在⊙O外部,
故答案为在圆外.
13.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=12,BC=5,
∴AC=13,
∵AN=NC,
∴BN=AC=6.5,
∵AN=NC,DM=MC,
∴MN=AD=2,
∴BN﹣MN≤BM≤BN+NM,
∴6.5﹣2≤BM≤6.5+2,即4.5≤BM≤8.5,
故答案为:4.5≤BM≤8.5.
14.解:设M点的坐标为(x,y),由题意知,MA=MB=MC,
∴,
化简得,x+y=﹣3x﹣3y+8=﹣2y+1,
即,
解得,
∴M.
故答案为:.
15.解:如图,
∵点C在线段AB上,且0<AC<AB,
∴BC>AC,
∴点B在⊙C外,
故答案为:点B在⊙C外.
三.解答题
16.解:(1)如图,圆心M的坐标为(2,0);
(2)∵A(0,4),M(2,0),
∴MA==2,
即⊙M的半径为2;
(3)∵D(5,﹣2),M(2,0),
∴DM==,
∵<2,
∴点D在⊙M内.
故答案为(2,0);2;内.
17.解:(1)∵A(0,2),B(2,0)
∴OA=2,OB=2;
Rt△OAB中,由勾股定理,得:AB==4;
∵∠AOB=90°,
∴AB是⊙C的直径;
∴⊙C的半径r=2;
过C作CE⊥y轴于E,则CE∥OB;
∵C是AB的中点,
∴CE是△AOB的中位线,
则OE=OA=1,CE=OB=,即C(,1);
故⊙C的半径为2,C(,1);
(2)如图,作OB的垂直平分线,交⊙C于P1、P2,交OB于D,连接OC;
由垂径定理知:P1P2必过点C,即P1P2是⊙C的直径;
∴P1(,3),P2(,﹣1);
在Rt△ODP1中,P1D=3,OD=,
∴∠BOP1=60°;
∵P1P2是直径,
∴∠P1OP2=90°,∠BOP2=30°;
由于P1P2垂直平分OB,所以△OBP1、△OBP2都是等腰三角形,因此P1、P2均符合P点的要求;
由于此时同时BO=P1O,因此不需要考虑BO为腰的情况.
故存在符合条件的P点:P1(,3),∠BOP1=60°;P2(,﹣1),∠BOP2=30°.
18.解:(1)如图,过点A作AE⊥BC于点E.
∵AB=AC,BC=4,
∴
∵,
∴AE=4,
∴
又
∴.
(2)如图,连结CD,过点D作DF⊥BC于点F,显然DF∥AE
∵点D是AB中点,即DF是中位线
∴,
∴CF=3
∴
又
∴r的取值范围是
