平行四边形的性质1
图片预览

文档简介
(共22张PPT)
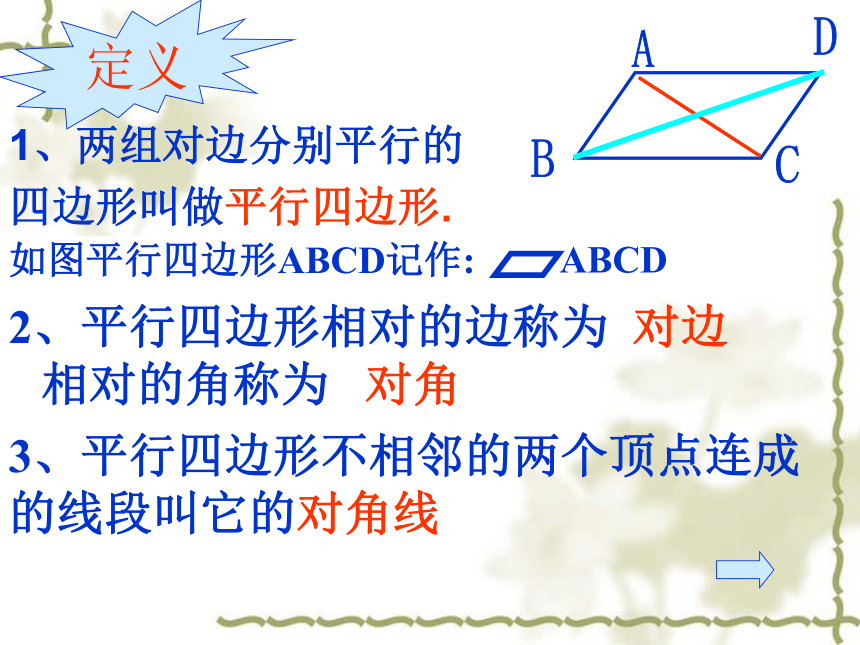
1、两组对边分别平行的
四边形叫做平行四边形.
定义
如图平行四边形ABCD记作:
3、平行四边形不相邻的两个顶点连成的线段叫它的对角线
2、平行四边形相对的边称为 对边 相对的角称为 对角
ABCD
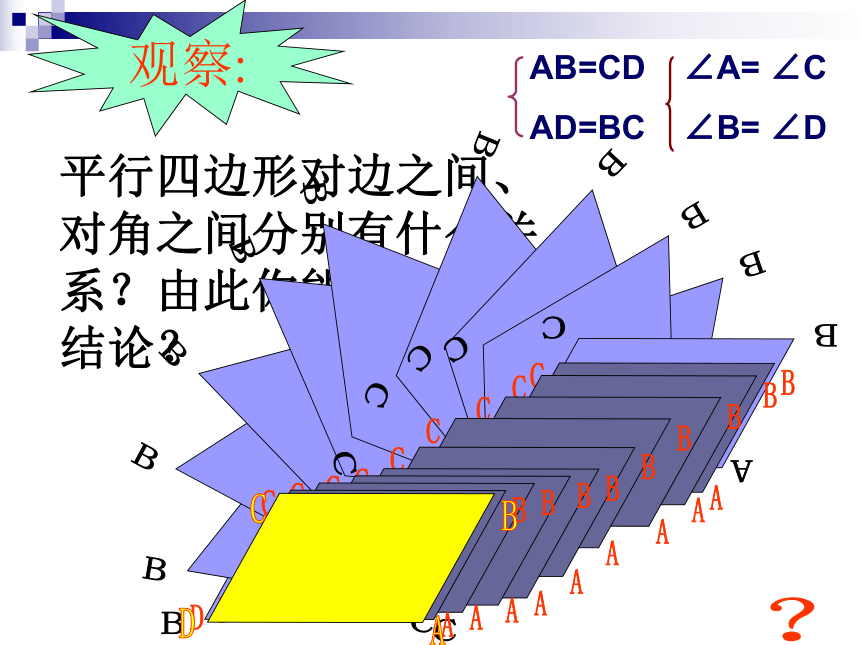
观察:
平行四边形对边之间、对角之间分别有什么关系?由此你能得到什么结论?
AB=CD
AD=BC
∠A= ∠C
∠B= ∠D
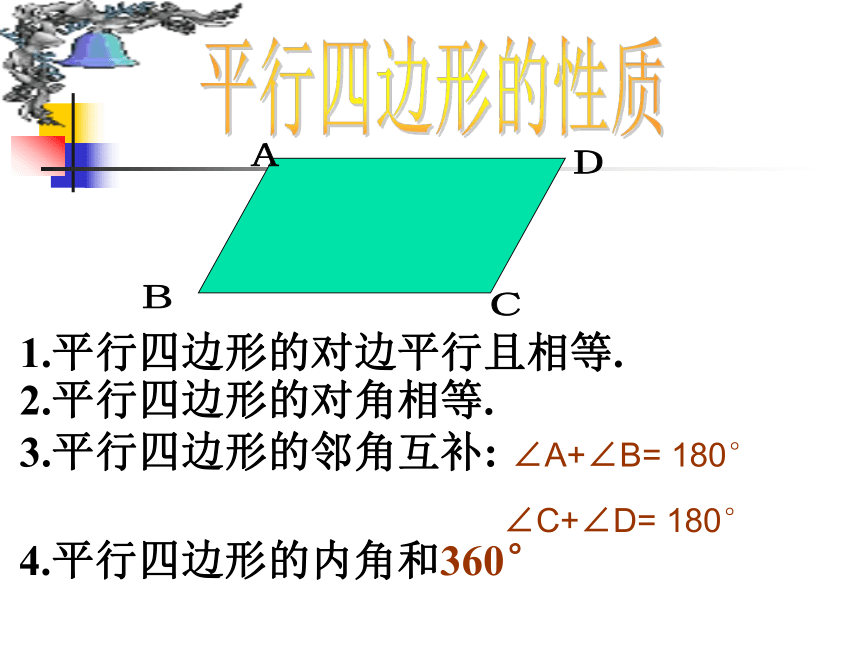
1.平行四边形的对边平行且相等.
3.平行四边形的邻角互补: ∠A+∠B= 180°
∠C+∠D= 180°
2.平行四边形的对角相等.
4.平行四边形的内角和360°
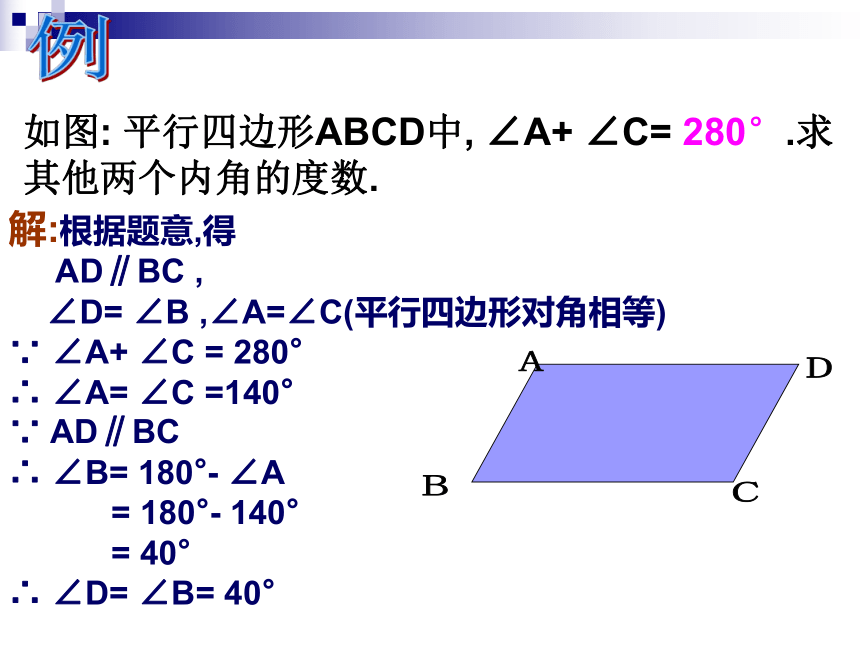
如图: 平行四边形ABCD中, ∠A+ ∠C= 280°.求
其他两个内角的度数.
解:根据题意,得
AD∥BC ,
∠D= ∠B ,∠A=∠C(平行四边形对角相等)
∵ ∠A+ ∠C = 280°
∴ ∠A= ∠C =140°
∵ AD∥BC
∴ ∠B= 180°- ∠A
= 180°- 140°
= 40°
∴ ∠D= ∠B= 40°
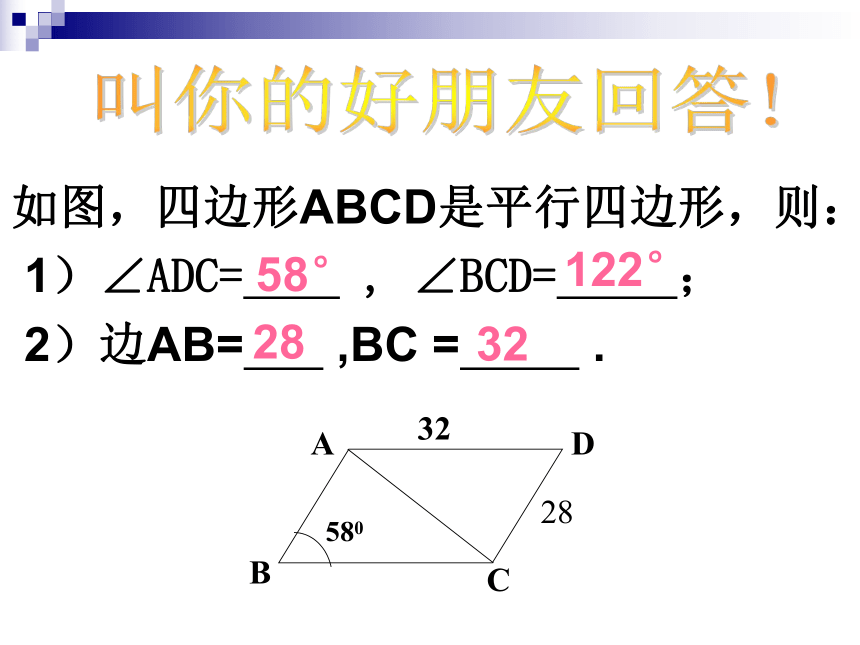
如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= ,BC = .
D
C
B
A
580
28
32
58°
28
32
122°
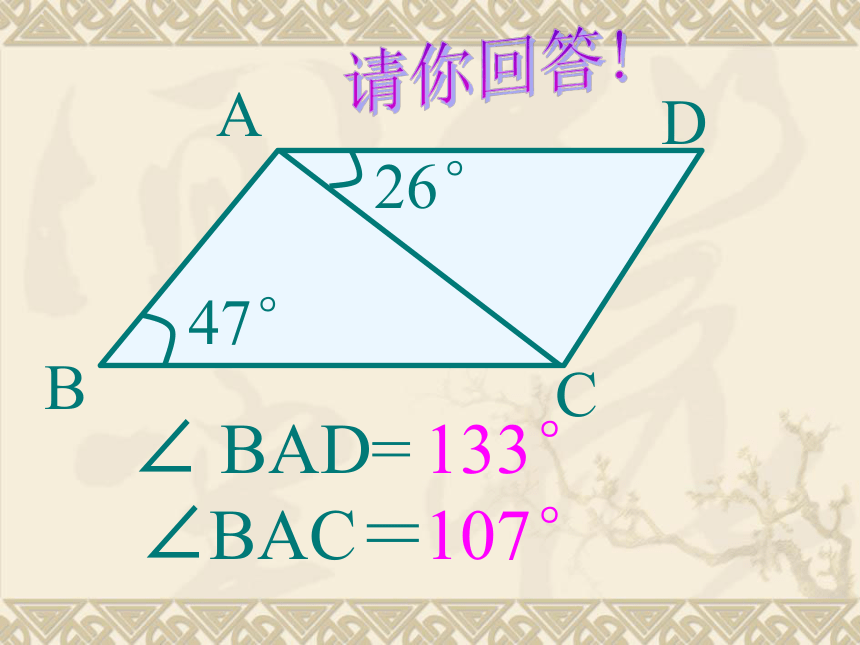
A
B
D
C
26°
47°
∠BAC=
107°
∠ BAD=
133°
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
C
D
A
B
O
我们讲中心对称图形的时候已经知道:以平行四边形的对角线交点O为旋转中心,旋转180后得到的图形会和原图形重合. ①也就是说:
②通过观察我们还发现了什么:
△AOB≌ △ COD(或者△ BOC ≌ △ DOA)
OA=OC OB=OD
已知: 点o是平行四边形两条对角线的交点, AC=24mm,BD=38mm,BC=28mm, 求△AOD的周长.
A
D
C
B
O
解:根据题意,得
AD=BC,OA=OC,OB=OD
∵BC=28,AC=24,BD=38
∴AD=28,OA=12,OD=19
∴△AOD的周长=AD+OA+OD
=28+12+19
=59mm
3cm
A
B
D
C
5cm
4cm
求平行四边形ABCD的面积
5cm
∟
A
B
D
C
E
9cm
5cm
若BE平分∠ABC,则ED=
4cm
1
2
3
5cm
5cm
4cm
在 ABCD中,已知两邻角的比∠A:∠B=5:4,求∠C ,∠D的度数.
解:根据题意,得
∠A+ ∠B= 180° ,
∠A=∠C , ∠D= ∠B .
∵ ∠A:∠B=5:4
∴ ∠A= 180° × = 100°
∠B= 180° × = 80°
5+4
5
5+4
4
∴ ∠C= ∠A= 100°
∠D=∠B= 80°
在 ABCD中,AC和BD相交
于点O, △AOB的周长为15,AB=6,
求对角线AC与BD的和是多少
C
D
A
B
O
∵△AOB的周长为15.
∴ AB+OB+OA=15
∵ AB=6
∴OB+OA=9
解:根据题意,得
AC=2OA, BD=2OB (平行四边形的对角线互相平分)
∴AC+BD= 2OA+2OB
=2(OA+OB)
=2×9
=18
通过本节课的学习,你有什么收获?
感悟与收获
1、平行四边形的定义
2、平行四边形的性质:
1.平行四边形的对边平行相等
2.平行四边形的对角相等
3.平行四边形的邻角互补
4.平行四边形是中心对称图形,它 的对称中心是两条对角线的交点.
5.平行四边形的对角线互相平分
6.平行四边形的内角和360°
1.已知平行四边形的周长是20厘米,一条
对角线把它分成的两个三角形的周长
都是18厘米.这条对角线长多少
2.在平行四边形中,两邻边的差是4厘米,
较短的一条边长是6厘米.求平行四边
形的周长.
3.平行四边形的周长为36厘米,一组邻边
之差为4厘米,求平行四边形各边长
4.在平行四边形中, ∠A: ∠B:∠C :∠D 的
值可以是( )
A . 1:2:3:4 B. 1:2:2:1
C. 1:1:2:2 D. 2:1:2:1
个
让我们大家一起来想
8cm
32cm
D
1、两组对边分别平行的
四边形叫做平行四边形.
定义
如图平行四边形ABCD记作:
3、平行四边形不相邻的两个顶点连成的线段叫它的对角线
2、平行四边形相对的边称为 对边 相对的角称为 对角
ABCD
观察:
平行四边形对边之间、对角之间分别有什么关系?由此你能得到什么结论?
AB=CD
AD=BC
∠A= ∠C
∠B= ∠D
1.平行四边形的对边平行且相等.
3.平行四边形的邻角互补: ∠A+∠B= 180°
∠C+∠D= 180°
2.平行四边形的对角相等.
4.平行四边形的内角和360°
如图: 平行四边形ABCD中, ∠A+ ∠C= 280°.求
其他两个内角的度数.
解:根据题意,得
AD∥BC ,
∠D= ∠B ,∠A=∠C(平行四边形对角相等)
∵ ∠A+ ∠C = 280°
∴ ∠A= ∠C =140°
∵ AD∥BC
∴ ∠B= 180°- ∠A
= 180°- 140°
= 40°
∴ ∠D= ∠B= 40°
如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= ,BC = .
D
C
B
A
580
28
32
58°
28
32
122°
A
B
D
C
26°
47°
∠BAC=
107°
∠ BAD=
133°
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
O
C
D
A
B
O
我们讲中心对称图形的时候已经知道:以平行四边形的对角线交点O为旋转中心,旋转180后得到的图形会和原图形重合. ①也就是说:
②通过观察我们还发现了什么:
△AOB≌ △ COD(或者△ BOC ≌ △ DOA)
OA=OC OB=OD
已知: 点o是平行四边形两条对角线的交点, AC=24mm,BD=38mm,BC=28mm, 求△AOD的周长.
A
D
C
B
O
解:根据题意,得
AD=BC,OA=OC,OB=OD
∵BC=28,AC=24,BD=38
∴AD=28,OA=12,OD=19
∴△AOD的周长=AD+OA+OD
=28+12+19
=59mm
3cm
A
B
D
C
5cm
4cm
求平行四边形ABCD的面积
5cm
∟
A
B
D
C
E
9cm
5cm
若BE平分∠ABC,则ED=
4cm
1
2
3
5cm
5cm
4cm
在 ABCD中,已知两邻角的比∠A:∠B=5:4,求∠C ,∠D的度数.
解:根据题意,得
∠A+ ∠B= 180° ,
∠A=∠C , ∠D= ∠B .
∵ ∠A:∠B=5:4
∴ ∠A= 180° × = 100°
∠B= 180° × = 80°
5+4
5
5+4
4
∴ ∠C= ∠A= 100°
∠D=∠B= 80°
在 ABCD中,AC和BD相交
于点O, △AOB的周长为15,AB=6,
求对角线AC与BD的和是多少
C
D
A
B
O
∵△AOB的周长为15.
∴ AB+OB+OA=15
∵ AB=6
∴OB+OA=9
解:根据题意,得
AC=2OA, BD=2OB (平行四边形的对角线互相平分)
∴AC+BD= 2OA+2OB
=2(OA+OB)
=2×9
=18
通过本节课的学习,你有什么收获?
感悟与收获
1、平行四边形的定义
2、平行四边形的性质:
1.平行四边形的对边平行相等
2.平行四边形的对角相等
3.平行四边形的邻角互补
4.平行四边形是中心对称图形,它 的对称中心是两条对角线的交点.
5.平行四边形的对角线互相平分
6.平行四边形的内角和360°
1.已知平行四边形的周长是20厘米,一条
对角线把它分成的两个三角形的周长
都是18厘米.这条对角线长多少
2.在平行四边形中,两邻边的差是4厘米,
较短的一条边长是6厘米.求平行四边
形的周长.
3.平行四边形的周长为36厘米,一组邻边
之差为4厘米,求平行四边形各边长
4.在平行四边形中, ∠A: ∠B:∠C :∠D 的
值可以是( )
A . 1:2:3:4 B. 1:2:2:1
C. 1:1:2:2 D. 2:1:2:1
个
让我们大家一起来想
8cm
32cm
D
