四年级下册数学课件人教版-三角形的内角和(23页ppt)
文档属性
| 名称 | 四年级下册数学课件人教版-三角形的内角和(23页ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 10:54:01 | ||
图片预览


文档简介
(共23张PPT)
第五单元(三角形)
人教版四年级数学下册
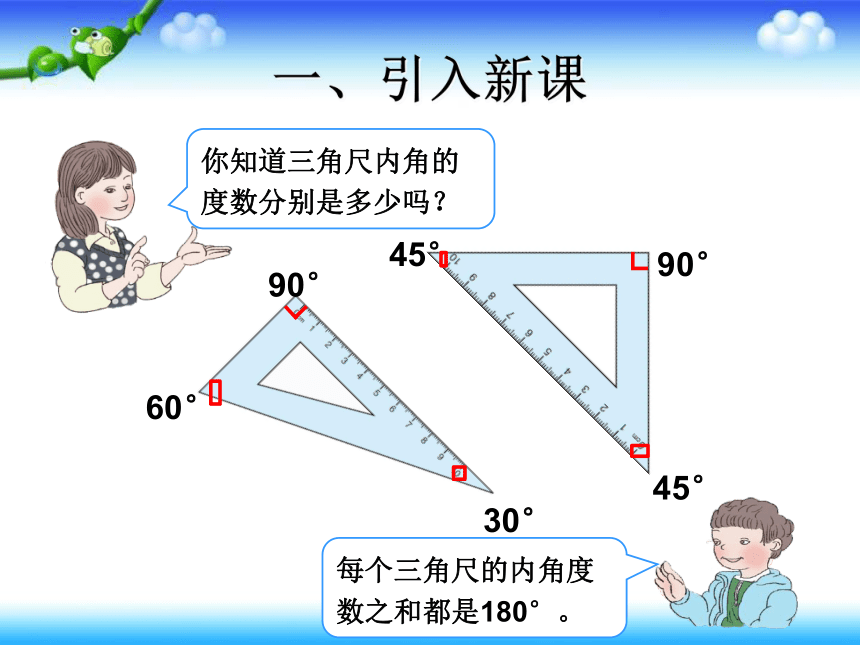
一、引入新课
30°
60°
90°
45°
90°
45°
你知道三角尺内角的
度数分别是多少吗?
每个三角尺的内角度
数之和都是180°。
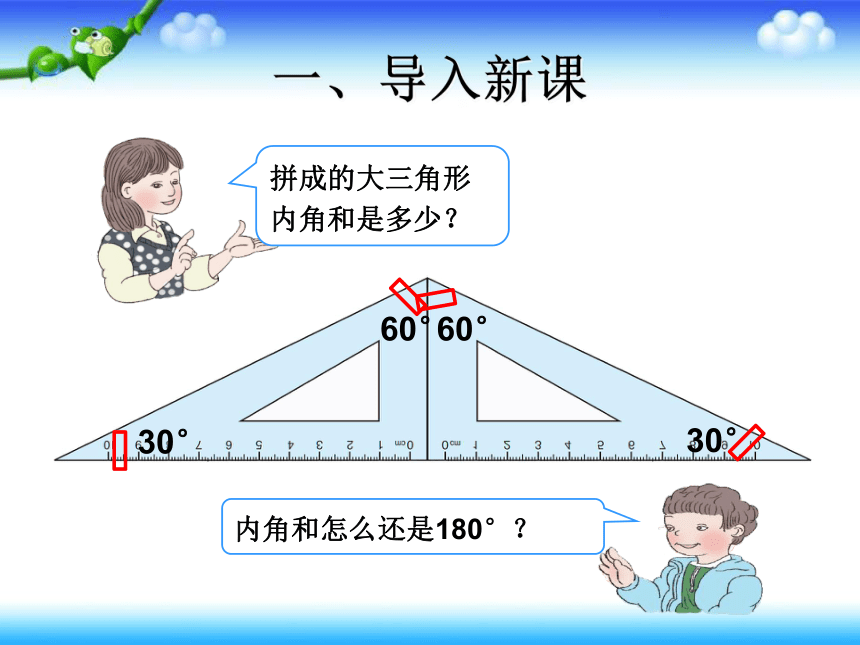
一、导入新课
拼成的大三角形内角和是多少?
内角和怎么还是180°?
30°
30°
60°
60°
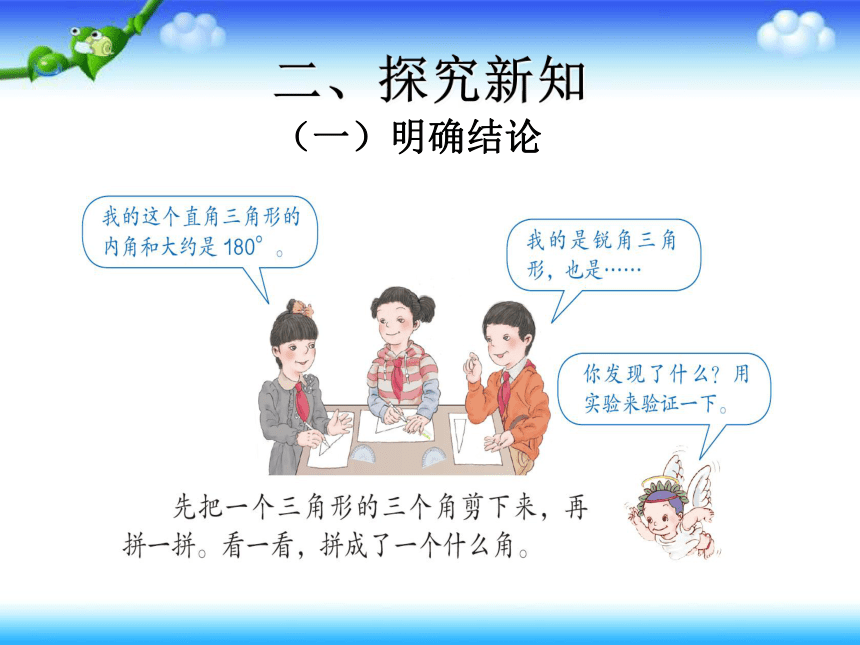
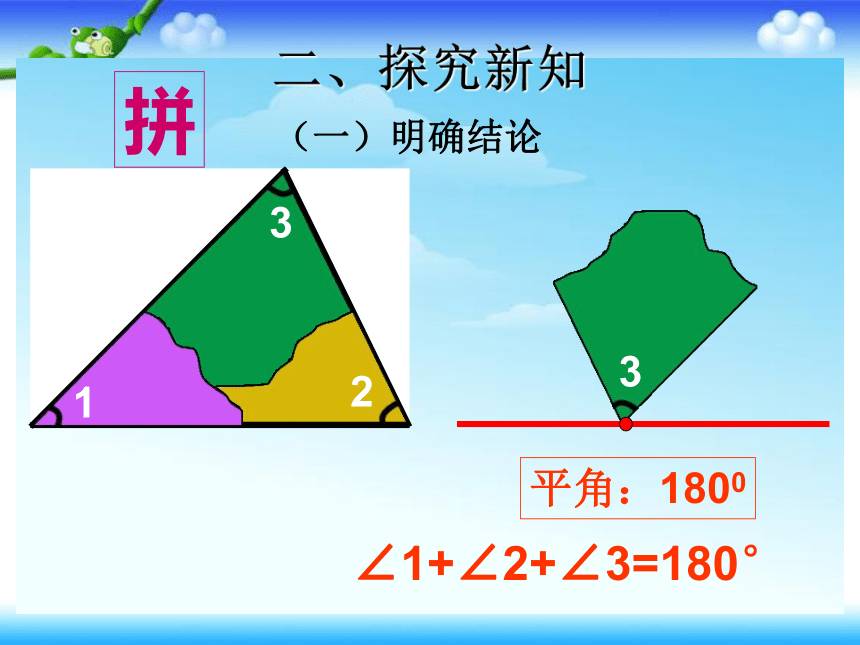
二、探究新知
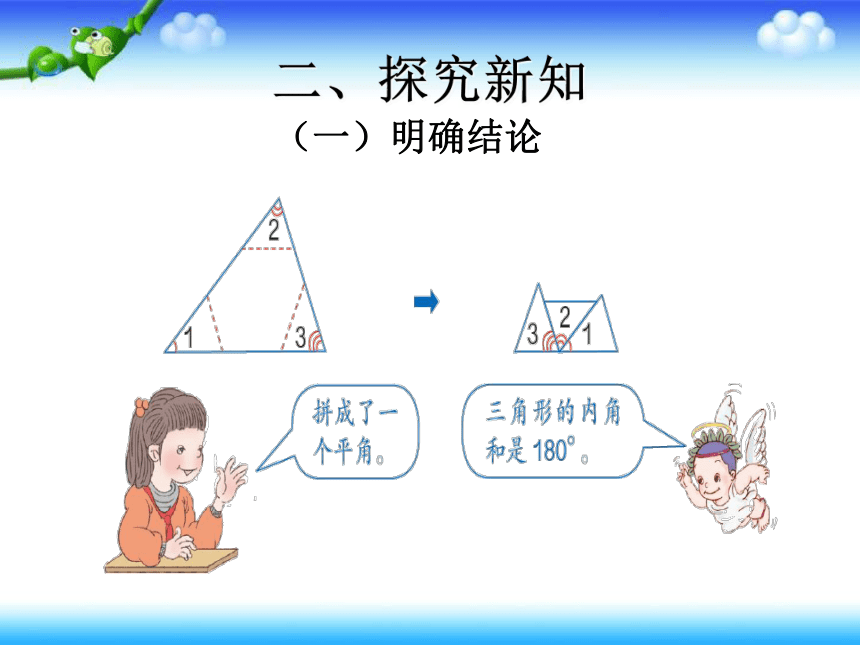
(一)明确结论
3
2
3
1
平角:1800
拼
∠1+∠2+∠3=180°
二、探究新知
(一)明确结论
二、探究新知
(一)明确结论
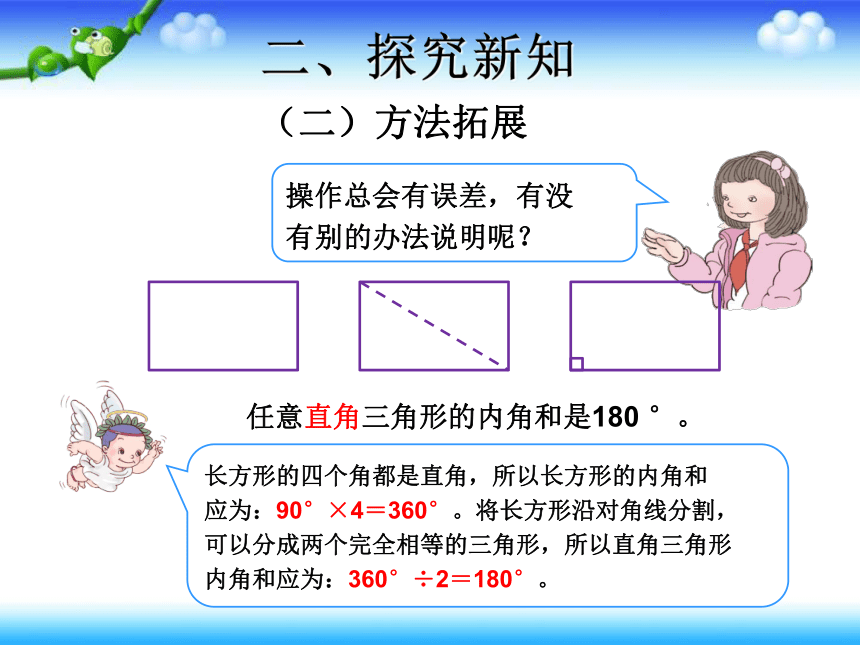
任意直角三角形的内角和是180
°。
(二)方法拓展
长方形的四个角都是直角,所以长方形的内角和
应为:90°×4=360°。将长方形沿对角线分割,
可以分成两个完全相等的三角形,所以直角三角形
内角和应为:360°÷2=180°。
二、探究新知
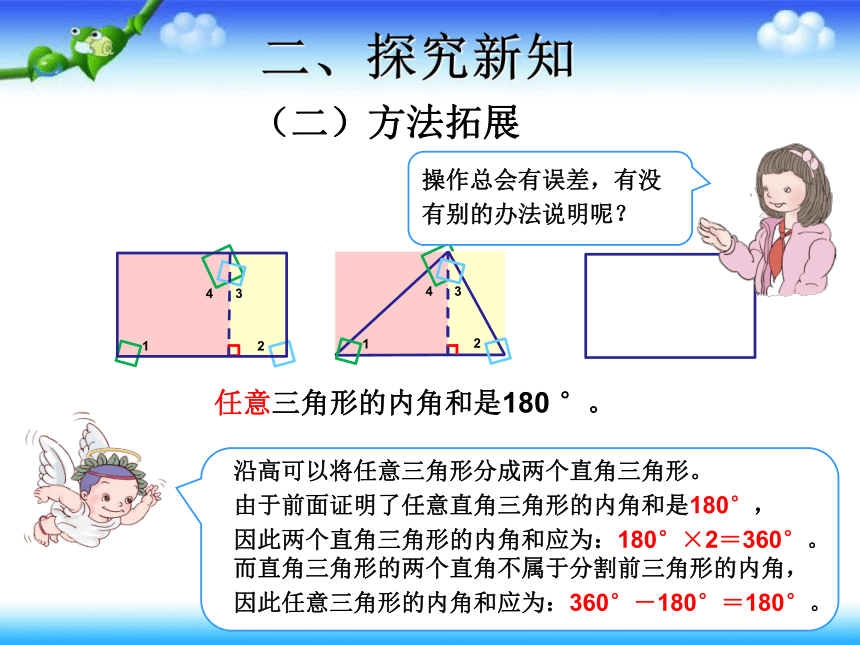
操作总会有误差,有没
有别的办法说明呢?
1
4
任意三角形的内角和是180
°。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°,
因此两个直角三角形的内角和应为:180°×2=360°。
而直角三角形的两个直角不属于分割前三角形的内角,
因此任意三角形的内角和应为:360°-180°=180°。
(二)方法拓展
1
2
3
4
2
3
操作总会有误差,有没有别的办法说明呢?
二、探究新知
法国著名数学家帕斯卡,在12岁时就已经发现了这种用直角三角形的内角和来证明其他三角形内角和是180
°的方法。
(二)方法拓展
二、探究新知
三角形不分大小、形状,内角和都是180°!
二、探究新知
(三)小结
1、在下图中,∠1=140°,∠3=25°。求∠2的度数。
∠2
=180°-140°-25°
=15°
140°
25°
或∠2
=180
°-(140°
+25°)
=15
°
三、知识运用
2.
这里有一条红领巾,它的形状是等腰三角形,其中∠1=110°,
请计算出∠2=(
)°,∠3=(
)°。
(180-110°)÷2=35°
35
35
三、知识运用
(1)∠1=35°
∠2=63°
∠3=(
)这是(
)三角形
(2)∠1=50°
∠2=40°
∠3=(
)
这是(
)
三角形
(3)∠1=20°
∠2=45°
∠3=(
)
这是(
)
三角形
3、填一填
82°
锐角
90°
直角
115°
钝角
三、知识运用
4、判一判:(下列说法对的打“√”,错的打“×”)
(1)钝角三角形的内角和大于锐角三角形的内角和。(
)
(2)把一个等腰三角形分成两个完全一样的小三角形,每个三角形的内角和都是90度。
(
)
(3)直角三角形的两个锐角和是90度。
(
)
(4)任何一个三角形的内角和都是180度。
(
)
×
×
√
√
三、知识运用
5、将一个大三角形分成两个小三角形,这两个小三角形的内角和分别是多少?
180°
三、知识运用
6.
剪一剪。
把一个三角形纸板沿直线剪一刀,剩下的纸板的内角和是多少度?
可能是三角形,内角和是180°,也可能是其他的情况。
三、知识运用
这节课,你有什么收获?
四、课堂总结,浅谈收获
三角形的内角和
1、知道任意三角形的内角和都是180°;
2、会应用三角形的内角和,计算三角形的内角。
五、布置课外作业
1、课本第69页练习十六,第1、2题。
2:《同步导学与优化训练》
第33页内容
课堂作业
(1)三角形的内角和是(
)。
(2)把一个三角形分成两个三角形,每个三角形的内角和是
(
)。
(3)把两个完全一样的三角形拼成一个大的三角形,这个大
三角形的内角和是(
)。
(4)一个直角三角形的一个锐角是35°,另一个锐角是
(
)。
1、填空
2、计算
在三角形中已知∠1=35°
∠2=57°求
∠3的度数。
(3)一个等腰三角形,一个底角是顶角的2倍,
这个三角形顶角(
)度,底角(
)度。
A.
36°
B.72°
C.45°
D.90°
(2)一个等腰三角形,顶角是100°,一个底角
是(
)。
A.100°
B.
40°
C.55°
(1)一个三角形中,有一个角是65°,另外的
两个角可能是(
)。
A.95°、20°
B.45°、80°
C.55°、60°
选一选
A、
C
A、
B
B
三、综合练习
五、布置课外作业
1、课本第69页练习十六,第3、题。
2:《同步导学与优化训练》
第33页内容
第五单元(三角形)
人教版四年级数学下册
一、引入新课
30°
60°
90°
45°
90°
45°
你知道三角尺内角的
度数分别是多少吗?
每个三角尺的内角度
数之和都是180°。
一、导入新课
拼成的大三角形内角和是多少?
内角和怎么还是180°?
30°
30°
60°
60°
二、探究新知
(一)明确结论
3
2
3
1
平角:1800
拼
∠1+∠2+∠3=180°
二、探究新知
(一)明确结论
二、探究新知
(一)明确结论
任意直角三角形的内角和是180
°。
(二)方法拓展
长方形的四个角都是直角,所以长方形的内角和
应为:90°×4=360°。将长方形沿对角线分割,
可以分成两个完全相等的三角形,所以直角三角形
内角和应为:360°÷2=180°。
二、探究新知
操作总会有误差,有没
有别的办法说明呢?
1
4
任意三角形的内角和是180
°。
沿高可以将任意三角形分成两个直角三角形。
由于前面证明了任意直角三角形的内角和是180°,
因此两个直角三角形的内角和应为:180°×2=360°。
而直角三角形的两个直角不属于分割前三角形的内角,
因此任意三角形的内角和应为:360°-180°=180°。
(二)方法拓展
1
2
3
4
2
3
操作总会有误差,有没有别的办法说明呢?
二、探究新知
法国著名数学家帕斯卡,在12岁时就已经发现了这种用直角三角形的内角和来证明其他三角形内角和是180
°的方法。
(二)方法拓展
二、探究新知
三角形不分大小、形状,内角和都是180°!
二、探究新知
(三)小结
1、在下图中,∠1=140°,∠3=25°。求∠2的度数。
∠2
=180°-140°-25°
=15°
140°
25°
或∠2
=180
°-(140°
+25°)
=15
°
三、知识运用
2.
这里有一条红领巾,它的形状是等腰三角形,其中∠1=110°,
请计算出∠2=(
)°,∠3=(
)°。
(180-110°)÷2=35°
35
35
三、知识运用
(1)∠1=35°
∠2=63°
∠3=(
)这是(
)三角形
(2)∠1=50°
∠2=40°
∠3=(
)
这是(
)
三角形
(3)∠1=20°
∠2=45°
∠3=(
)
这是(
)
三角形
3、填一填
82°
锐角
90°
直角
115°
钝角
三、知识运用
4、判一判:(下列说法对的打“√”,错的打“×”)
(1)钝角三角形的内角和大于锐角三角形的内角和。(
)
(2)把一个等腰三角形分成两个完全一样的小三角形,每个三角形的内角和都是90度。
(
)
(3)直角三角形的两个锐角和是90度。
(
)
(4)任何一个三角形的内角和都是180度。
(
)
×
×
√
√
三、知识运用
5、将一个大三角形分成两个小三角形,这两个小三角形的内角和分别是多少?
180°
三、知识运用
6.
剪一剪。
把一个三角形纸板沿直线剪一刀,剩下的纸板的内角和是多少度?
可能是三角形,内角和是180°,也可能是其他的情况。
三、知识运用
这节课,你有什么收获?
四、课堂总结,浅谈收获
三角形的内角和
1、知道任意三角形的内角和都是180°;
2、会应用三角形的内角和,计算三角形的内角。
五、布置课外作业
1、课本第69页练习十六,第1、2题。
2:《同步导学与优化训练》
第33页内容
课堂作业
(1)三角形的内角和是(
)。
(2)把一个三角形分成两个三角形,每个三角形的内角和是
(
)。
(3)把两个完全一样的三角形拼成一个大的三角形,这个大
三角形的内角和是(
)。
(4)一个直角三角形的一个锐角是35°,另一个锐角是
(
)。
1、填空
2、计算
在三角形中已知∠1=35°
∠2=57°求
∠3的度数。
(3)一个等腰三角形,一个底角是顶角的2倍,
这个三角形顶角(
)度,底角(
)度。
A.
36°
B.72°
C.45°
D.90°
(2)一个等腰三角形,顶角是100°,一个底角
是(
)。
A.100°
B.
40°
C.55°
(1)一个三角形中,有一个角是65°,另外的
两个角可能是(
)。
A.95°、20°
B.45°、80°
C.55°、60°
选一选
A、
C
A、
B
B
三、综合练习
五、布置课外作业
1、课本第69页练习十六,第3、题。
2:《同步导学与优化训练》
第33页内容
