21.2.4 一元二次方程的根与系数的关系 课件(共22张PPT)
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 16:23:37 | ||
图片预览




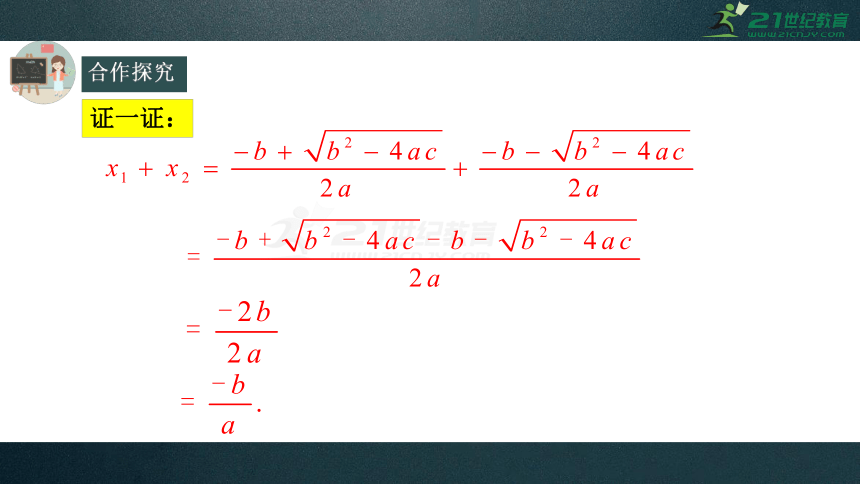
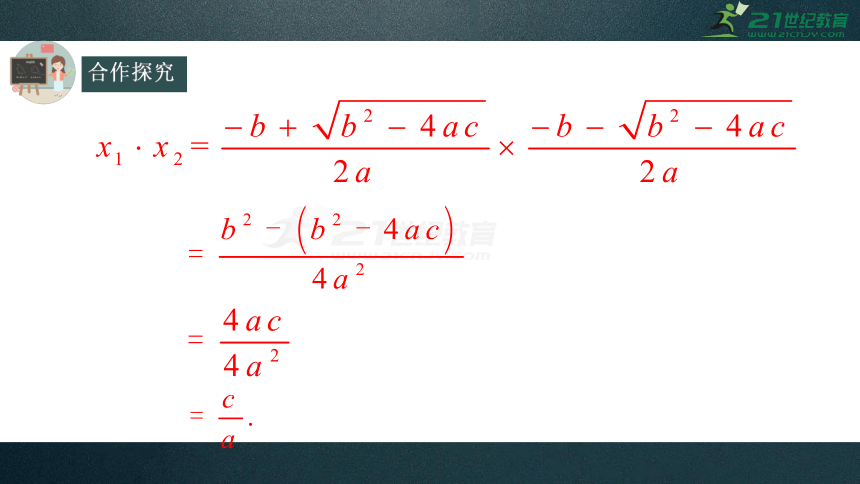

文档简介
(共22张PPT)
人教版
九年级数学上
21.2.4一元二次方程的根与系数的关系
学习目标
1.熟练掌握一元二次方程的根与系数的关系.(重点)
2.灵活利用一元二次方程的根与系数的关系解决问题.(难点)
回顾旧知
1.
一元二次方程的求根公式是什么?
2.
方程的两根x1,x2与系数a,b,c之间的联系还有其他表现形式吗?
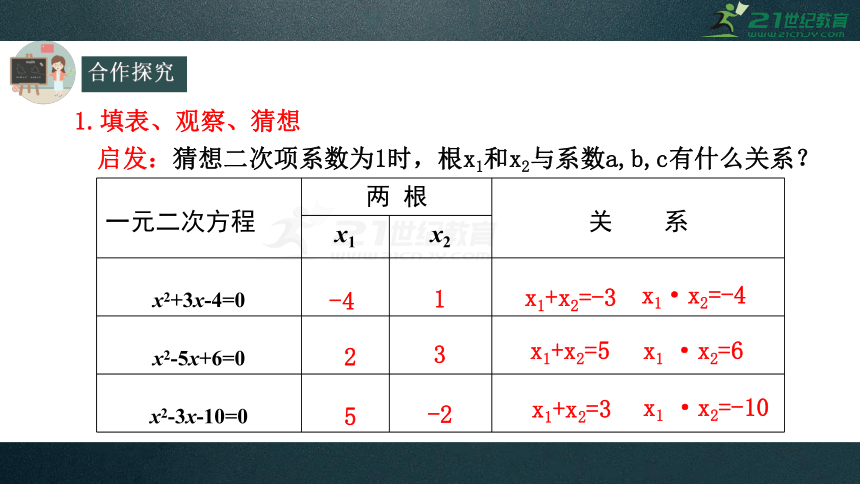
合作探究
1.填表、观察、猜想
启发:猜想二次项系数为1时,根x1和x2与系数a,b,c有什么关系?
一元二次方程
两
根
关
系
x1
x2
x2+3x-4=0
x2-5x+6=0
x2-3x-10=0
-4
1
2
3
-2
x1+x2=-3
x1·x2=-4
x1+x2=5
x1
·x2=6
5
x1+x2=3
x1
·x2=-10
合作探究
思考1:从因式分解可知,方程(x-x1)(x-x2)=0(x1、x2已知数)的两根为x1,x2,将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
★归纳:
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=
-p,
x1
·x2=q.
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
x1+x2=
-p
,
x1
·x2=q.
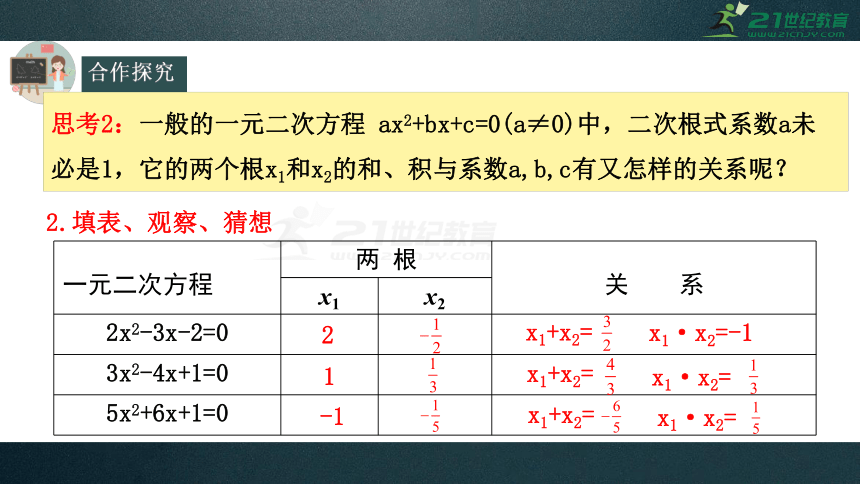
合作探究
思考2:一般的一元二次方程
ax2+bx+c=0(a≠0)中,二次根式系数a未必是1,它的两个根x1和x2的和、积与系数a,b,c有又怎样的关系呢?
2.填表、观察、猜想
2
一元二次方程
两
根
关
系
x1
x2
2x2-3x-2=0
3x2-4x+1=0
5x2+6x+1=0
x1+x2=
x1·x2=-1
1
-1
x1+x2=
x1·x2=
x1+x2=
x1·x2=
合作探究
证一证:
合作探究
要点归纳
一元二次方程的根与系数的关系
(韦达定理)
如果
ax2+bx+c=0(a≠0)的两个根为x1、
x2,那么两根之和等于方程一次项系数与二次项系数的比的相反数;两根之积等于常数项与二次项系数的比;即:
温馨提示:满足上述关系的前提条件:
1.将方程化为一般形式:
ax2+bx+c=0(a≠0)2.b2=4ac≥0
典例精析
例
利用根与系数的关系,求下列方程的两根之和、两根之积.
(1)x2
–
6x
–
15
=
0;
解:a
=
1
,
b
=
–
6
,
c
=
–
15
.
x1
+
x2
=
–(
–
6
)
=6,
x1
x2
=
–
15
.
(2)3x2
+7x-9
=
0;
x1
+
x2
=-
,
x1
x2
=
解:
a
=
3
,
b
=
7,
c
=
-9.
典例精析
(3)
5x
–
1
=
4x2
.
解:方程可化为
4x2
–
5x
+1
=0,
a
=4,
b
=
–
5,c
=
1.
x1
+
x2
=
,
x1
x2
=
.
知识点拨:在运用韦达定理求两根之和、两根之积时,先把方程化为一般式,再分别代入a、b、c的值即可
.
小试牛刀
1.不解方程,求下列方程两个根的和与积:
(1)x2-3x=15;
(2)3x2+2=1-4x;
(3)5x2-1=4x2+x;
解:(1)方程化为
x2-3x-15=0
∴x1+x2=3,
x1x2=-15
(2)方程化为
3x2+4x+1
(3)方程化为
x2-x-1=0
∴x1+x2
=1,
x1x2
=-1
∴
x1
+
x2
=-
,
x1
x2
=
小试牛刀
2、已知方程4x2+ax-8=0的一个根是2,求它的另一个根及a的值.
解:设方程的两个根分别是x1、x2,其中x1=2
.
∴
x1·x2=2
x2
=
即
x2=
∵x1+x2=2+
=
得:
a=-4.
答:方程的另一个根是
-1
,a=-4.
小试牛刀
3、不解方程,求方程2x2+3x-5=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
常见的求值式子:
综合演练
1.已知一元二次方程x2+px+q=0的两根分别为4
和-6
,则p=
,
q=
.
-24
2
2.如果-1是方程3x2-2x+k=0的一个根,则另一个根是___,k
=____.
-5
3.已知关于x的方程x2-(m+1)x+2m-1=0。
(1)当m=_____时,此方程的两根互为相反数。
(2)当m=_____时,此方程的两根互为倒数。
-1
1
综合演练
4、设x1,x2是方程
x2
+2(k-1)x
+
k2
=0
的两个实数根,且x12
+x22
=14,
求k的值.
解:由方程有两个实数根,得Δ=
4(k-1)2
-
4k2
≥
0
即
-8k
+
4
≥
0.
由根与系数的关系得
x1
+
x2
=
-2(k
-1)
,
x1
x2
=k
2.
∴
x12
+
x22
=
(x1
+
x2)2
-
2x1x2
=
4(k
-1)2
-2k2
=
2k2
-8k
+
4.
由
x12
+
x22
=
4,得
2k2
-
8k
+
4
=14,
解得
k1=
-1,
k2
=
5
.
经检验,
k2
=
5
不合题意,舍去.所以
k=-1.
综合演练
5.已知关于x的一元二次方程ax2-2ax+a
-2=0.
(1)若方程有实数根,求实数a的取值范围.
(2)若方程两根x1,x2满足|x1-x2|=
1,
求m的值.
解:(1)方程有实数根
∵a≠0,∴a>0.
(2)∵方程有实数根x1,x2,
∵
(|x1-x2|)2
=
(x1-x2)2
=(x1+x2)2-4x1x2=1,
解得a=8.
经检验a=8是方程的解.
能力提升
6、已知关于m2+2m-2009=0,n2+2n-2009=0(m≠n),求(m-1)(n-1).
解:由已知条件,得m,n是方程x2+2x-2009=0的两个不相等的
实数根;
由韦达定理:m+n=-2,mn=-2009
(m-1)(n-1)
=mn-(m+n)+1
=-2009-(-2)+1
=-2006
课堂小结
本节课你有哪些收获?
1、一元二次方程的根与系数的关系是什么?
2、常见的求值式子有哪些?
课后作业
教材17页习题21.2第7题.
https://www.21cnjy.com/help/help_extract.php
人教版
九年级数学上
21.2.4一元二次方程的根与系数的关系
学习目标
1.熟练掌握一元二次方程的根与系数的关系.(重点)
2.灵活利用一元二次方程的根与系数的关系解决问题.(难点)
回顾旧知
1.
一元二次方程的求根公式是什么?
2.
方程的两根x1,x2与系数a,b,c之间的联系还有其他表现形式吗?
合作探究
1.填表、观察、猜想
启发:猜想二次项系数为1时,根x1和x2与系数a,b,c有什么关系?
一元二次方程
两
根
关
系
x1
x2
x2+3x-4=0
x2-5x+6=0
x2-3x-10=0
-4
1
2
3
-2
x1+x2=-3
x1·x2=-4
x1+x2=5
x1
·x2=6
5
x1+x2=3
x1
·x2=-10
合作探究
思考1:从因式分解可知,方程(x-x1)(x-x2)=0(x1、x2已知数)的两根为x1,x2,将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
★归纳:
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2=
-p,
x1
·x2=q.
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
x1+x2=
-p
,
x1
·x2=q.
合作探究
思考2:一般的一元二次方程
ax2+bx+c=0(a≠0)中,二次根式系数a未必是1,它的两个根x1和x2的和、积与系数a,b,c有又怎样的关系呢?
2.填表、观察、猜想
2
一元二次方程
两
根
关
系
x1
x2
2x2-3x-2=0
3x2-4x+1=0
5x2+6x+1=0
x1+x2=
x1·x2=-1
1
-1
x1+x2=
x1·x2=
x1+x2=
x1·x2=
合作探究
证一证:
合作探究
要点归纳
一元二次方程的根与系数的关系
(韦达定理)
如果
ax2+bx+c=0(a≠0)的两个根为x1、
x2,那么两根之和等于方程一次项系数与二次项系数的比的相反数;两根之积等于常数项与二次项系数的比;即:
温馨提示:满足上述关系的前提条件:
1.将方程化为一般形式:
ax2+bx+c=0(a≠0)2.b2=4ac≥0
典例精析
例
利用根与系数的关系,求下列方程的两根之和、两根之积.
(1)x2
–
6x
–
15
=
0;
解:a
=
1
,
b
=
–
6
,
c
=
–
15
.
x1
+
x2
=
–(
–
6
)
=6,
x1
x2
=
–
15
.
(2)3x2
+7x-9
=
0;
x1
+
x2
=-
,
x1
x2
=
解:
a
=
3
,
b
=
7,
c
=
-9.
典例精析
(3)
5x
–
1
=
4x2
.
解:方程可化为
4x2
–
5x
+1
=0,
a
=4,
b
=
–
5,c
=
1.
x1
+
x2
=
,
x1
x2
=
.
知识点拨:在运用韦达定理求两根之和、两根之积时,先把方程化为一般式,再分别代入a、b、c的值即可
.
小试牛刀
1.不解方程,求下列方程两个根的和与积:
(1)x2-3x=15;
(2)3x2+2=1-4x;
(3)5x2-1=4x2+x;
解:(1)方程化为
x2-3x-15=0
∴x1+x2=3,
x1x2=-15
(2)方程化为
3x2+4x+1
(3)方程化为
x2-x-1=0
∴x1+x2
=1,
x1x2
=-1
∴
x1
+
x2
=-
,
x1
x2
=
小试牛刀
2、已知方程4x2+ax-8=0的一个根是2,求它的另一个根及a的值.
解:设方程的两个根分别是x1、x2,其中x1=2
.
∴
x1·x2=2
x2
=
即
x2=
∵x1+x2=2+
=
得:
a=-4.
答:方程的另一个根是
-1
,a=-4.
小试牛刀
3、不解方程,求方程2x2+3x-5=0的两根的平方和、倒数和.
解:根据根与系数的关系可知:
常见的求值式子:
综合演练
1.已知一元二次方程x2+px+q=0的两根分别为4
和-6
,则p=
,
q=
.
-24
2
2.如果-1是方程3x2-2x+k=0的一个根,则另一个根是___,k
=____.
-5
3.已知关于x的方程x2-(m+1)x+2m-1=0。
(1)当m=_____时,此方程的两根互为相反数。
(2)当m=_____时,此方程的两根互为倒数。
-1
1
综合演练
4、设x1,x2是方程
x2
+2(k-1)x
+
k2
=0
的两个实数根,且x12
+x22
=14,
求k的值.
解:由方程有两个实数根,得Δ=
4(k-1)2
-
4k2
≥
0
即
-8k
+
4
≥
0.
由根与系数的关系得
x1
+
x2
=
-2(k
-1)
,
x1
x2
=k
2.
∴
x12
+
x22
=
(x1
+
x2)2
-
2x1x2
=
4(k
-1)2
-2k2
=
2k2
-8k
+
4.
由
x12
+
x22
=
4,得
2k2
-
8k
+
4
=14,
解得
k1=
-1,
k2
=
5
.
经检验,
k2
=
5
不合题意,舍去.所以
k=-1.
综合演练
5.已知关于x的一元二次方程ax2-2ax+a
-2=0.
(1)若方程有实数根,求实数a的取值范围.
(2)若方程两根x1,x2满足|x1-x2|=
1,
求m的值.
解:(1)方程有实数根
∵a≠0,∴a>0.
(2)∵方程有实数根x1,x2,
∵
(|x1-x2|)2
=
(x1-x2)2
=(x1+x2)2-4x1x2=1,
解得a=8.
经检验a=8是方程的解.
能力提升
6、已知关于m2+2m-2009=0,n2+2n-2009=0(m≠n),求(m-1)(n-1).
解:由已知条件,得m,n是方程x2+2x-2009=0的两个不相等的
实数根;
由韦达定理:m+n=-2,mn=-2009
(m-1)(n-1)
=mn-(m+n)+1
=-2009-(-2)+1
=-2006
课堂小结
本节课你有哪些收获?
1、一元二次方程的根与系数的关系是什么?
2、常见的求值式子有哪些?
课后作业
教材17页习题21.2第7题.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
