冀教版数学七年级上册2.7角的和与差 (共27张ppt)
文档属性
| 名称 | 冀教版数学七年级上册2.7角的和与差 (共27张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 16:44:10 | ||
图片预览




文档简介
(共27张PPT)
O
A
C
B
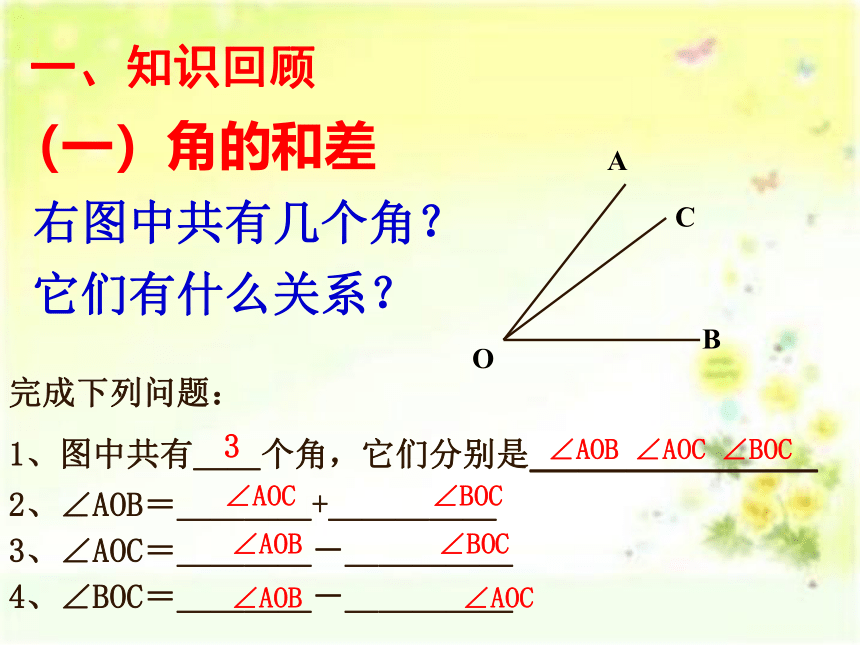
右图中共有几个角?
它们有什么关系?
完成下列问题:
1、图中共有__个角,它们分别是______
2、∠AOB=____+_____
3、∠AOC=____-_____
4、∠BOC=____-_____
3
∠AOB ∠AOC ∠BOC
∠AOC ∠BOC
∠AOB ∠BOC
∠AOB ∠AOC
一、知识回顾
(一)角的和差
60°
40°
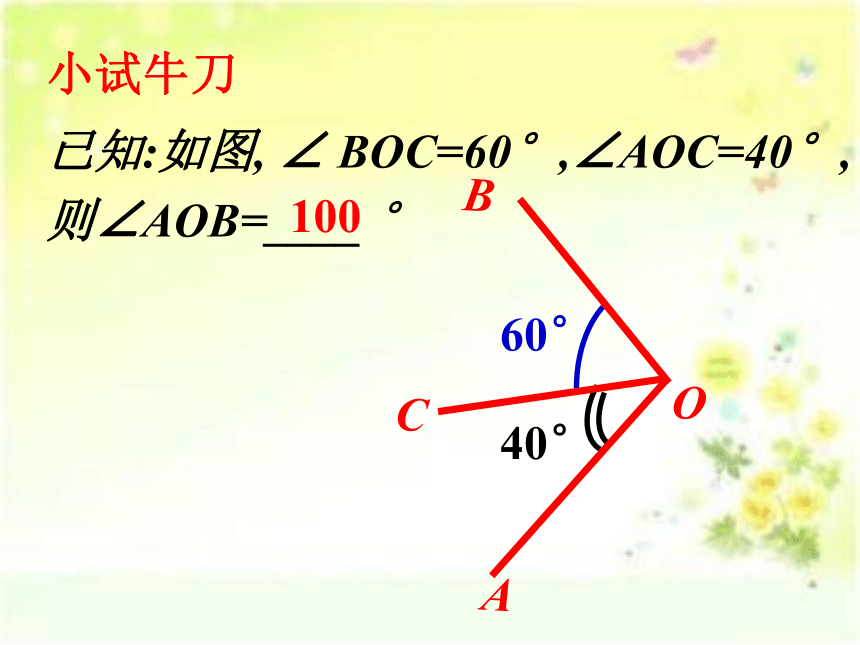
已知:如图, ∠ BOC=60°,∠AOC=40°,
则∠AOB=____ °
B
A
O
C
100
小试牛刀
B
A
O
C
105°
65°
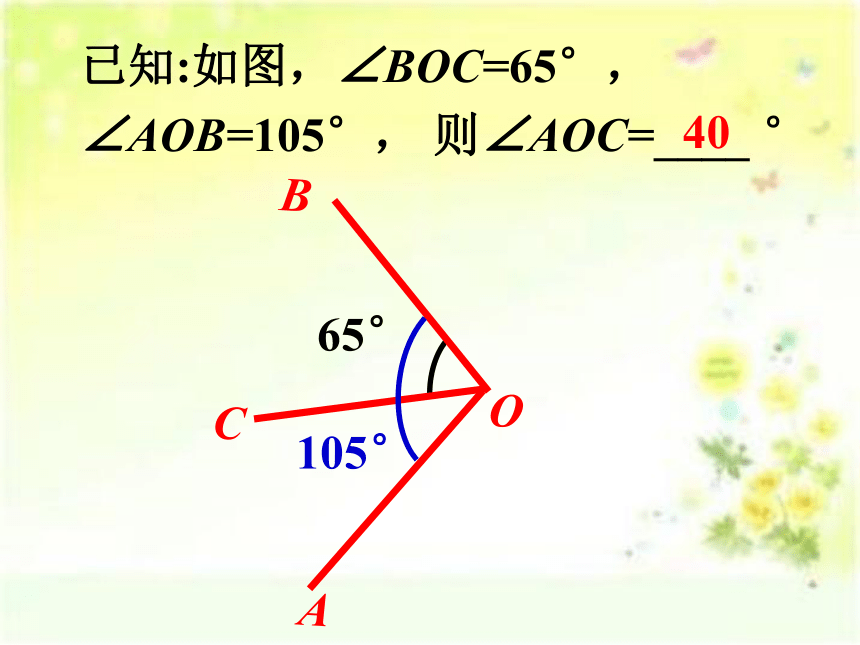
40
已知:如图,∠BOC=65°, ∠AOB=105°, 则∠AOC=____ °
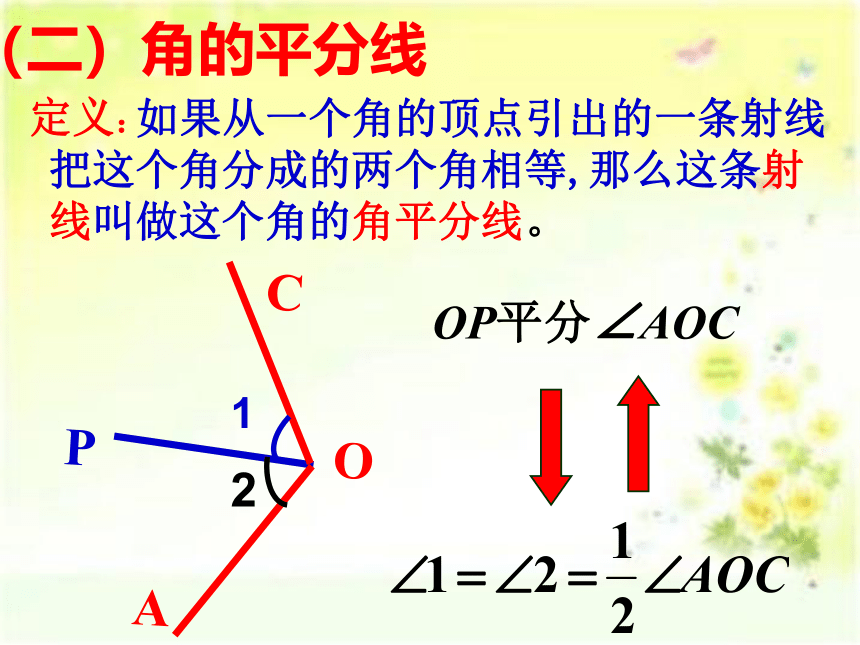
如果从一个角的顶点引出的一条射线把这个角分成的两个角相等,那么这条射线叫做这个角的角平分线。
P
A
O
C
定义:
OP平分∠AOC
1
2
(二)角的平分线
例:已知∠1=103°24′28″,∠2=30°54″,
求∠1+ ∠2和∠1-∠2的度数.
二、合作探究
(一)角的和差计算
103°24′28″
30° 54″
+
133°24′ 82″
(82″=1′22 ″)
解: ∠1+∠2 = 103°24′28″+ 30°54 ″
所以 ∠ AOB=∠1+∠2=133°25′22″
103°24′28″
∠1-∠2= 103°24′28″- 30°54 ″
所以∠1-∠2=73°23′34″
73°23′34″
-
30° 54″
103°24′28″
(24′28″=23′88 ″)
试一试
课本P84习题A组第1题
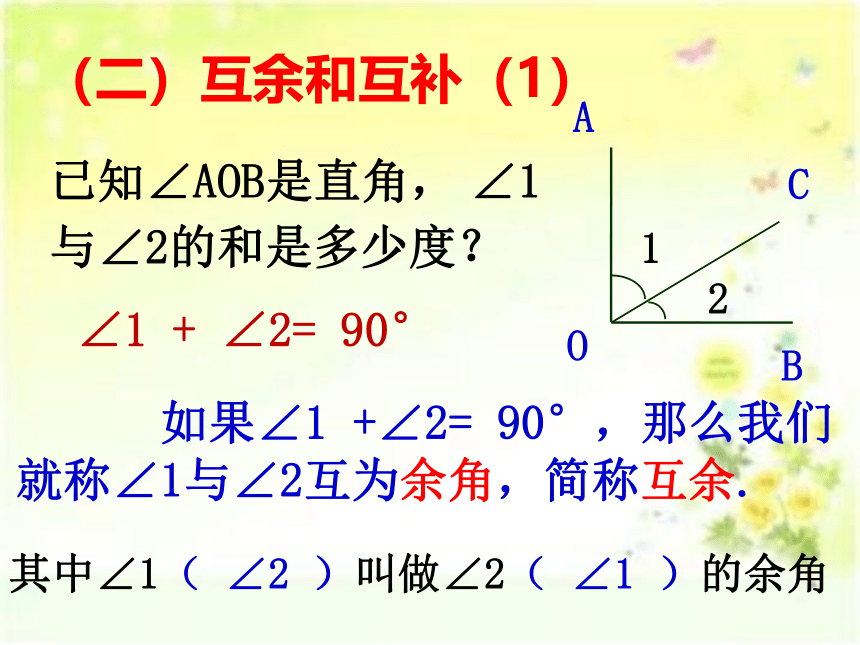
(二)互余和互补(1)
1
2
A
B
C
O
已知∠AOB是直角, ∠1与∠2的和是多少度?
∠1 + ∠2= 90°
如果∠1 +∠2= 90°,那么我们就称∠1与∠2互为余角,简称互余.
其中∠1( ∠2 )叫做∠2( ∠1 )的余角
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
(二)互余和互补(2)
已知∠AOB是平角, ∠1与∠2的和是多少度?
∠1 + ∠2= 180°
如果∠1 +∠2= 180°,那么我们就称∠1与∠2互为补角,简称互补.
其中∠1( ∠2 )叫做∠2( ∠1 )的补角
C
B
A
O
2
1
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x
90° x
180° x
试一试
想一想:1、钝角有余角吗?
没有
2、直角有余角吗?
没有
3、同一个角的补角比它的
余角大多少度?
90°
1、90度的角叫余角,180度的角叫补角( )
3、如果一个角有补角,那么这个角一定是钝角( )
5、互补的两个角不可能相等。 ( )
4、钝角没有余角,但一定有补角。( )
6、互余的两个角一定都是锐角,两个锐角一定互余.
( )
2、若∠1 + ∠2+ ∠3 =90 °,则∠1 ,∠2, ∠3 互余。 ( )
7、如果 ( )
辨一辨
(三)余角和补角的性质
探究1:
C
D
2
1
3
O
A
B
如图:已知∠1与 ∠2互余, ∠3与 ∠2互余,那么∠1与 ∠3有什么关系?为什么?
相等 ∵ ∠1与 ∠2互余, ∠3与 ∠2互余
∴ ∠1 + ∠2 =90 °
∠3 + ∠2 =90 °
∴ ∠1 = 90°-∠2
∠3 = 90°-∠2
∴ ∠1 = ∠3
同角的余角相等。
C
A
B
D
1
2
3
4
探究2 已知:A、D、B在同一直线上,DC⊥AB,∠1 =∠2
则∠3、∠4关系如何?为什么?
分析:因为DC⊥AB (已知)
所以∠ADC=∠BDC = 。
所以∠1+ ∠3 = °移项得∠3= 。
∠2+ ∠4 = °移项得∠4= 。
因为∠1 =∠2 所以∠3 ∠4
90°
90
90 °-∠1
90
90 °-∠2
=
同角(或等角)的补角 .
同角(或等角)的余角相等 .
相等
余角的性质
你能用数学语言说明一下吗?
补角的性质
课本P83 练习题2
如图O是直线AB上一点,OE平分∠AOC,OD平分∠BOC,那么图中共有:
几对相等的角
(2) 几对互余的角
(3)几对互补的角
解: 相等的角2对: ∠1 = ∠2 , ∠3= ∠4
互余的角4对: ∠2与∠3, ∠1与 ∠4 ∠1与 ∠3, ∠2 与∠4
互补的角5对: ∠1与∠BOE, ∠4与∠AOD, ∠AOC与∠BOC,∠2 与BOE, ∠3与∠AOD
A
B
E
C
D
1
2
3
4
O
三、拓展提高
总结收获
畅谈体会
LOVE
2、余角、补角的概念:
3、余角、补角的性质:
谈谈你的收获?
1、角的和差计算
互余的角 互补的角
数量关系
对应图形
性质
C
D
E
N
A
O
B
M
1+ 2=90°
1+ 2=180°
同角(等角)的余角相等
同角(等角)的补角相等
四、家庭作业
练习题P63--65
一个角的余角是这个角的2倍,求这个角。
例题欣赏
解:设这个角为x °,则它的余角为 。
由题意可列方程 。
解得 。
答:这个角为 。
分析:用代数里设未知数列方程的方法来解
几何问题,是一种常见的解题思路。不妨你来试
一试吧!
(2x)°
X+2x=90
x=30
30 °
解:设这个角为x °,则它的余角为 。
由题意可列方程 。
解得 。
答:这个角为 。
(90-x)°
90-x=2x
x=30
30 °
方法二
O
A
C
B
右图中共有几个角?
它们有什么关系?
完成下列问题:
1、图中共有__个角,它们分别是______
2、∠AOB=____+_____
3、∠AOC=____-_____
4、∠BOC=____-_____
3
∠AOB ∠AOC ∠BOC
∠AOC ∠BOC
∠AOB ∠BOC
∠AOB ∠AOC
一、知识回顾
(一)角的和差
60°
40°
已知:如图, ∠ BOC=60°,∠AOC=40°,
则∠AOB=____ °
B
A
O
C
100
小试牛刀
B
A
O
C
105°
65°
40
已知:如图,∠BOC=65°, ∠AOB=105°, 则∠AOC=____ °
如果从一个角的顶点引出的一条射线把这个角分成的两个角相等,那么这条射线叫做这个角的角平分线。
P
A
O
C
定义:
OP平分∠AOC
1
2
(二)角的平分线
例:已知∠1=103°24′28″,∠2=30°54″,
求∠1+ ∠2和∠1-∠2的度数.
二、合作探究
(一)角的和差计算
103°24′28″
30° 54″
+
133°24′ 82″
(82″=1′22 ″)
解: ∠1+∠2 = 103°24′28″+ 30°54 ″
所以 ∠ AOB=∠1+∠2=133°25′22″
103°24′28″
∠1-∠2= 103°24′28″- 30°54 ″
所以∠1-∠2=73°23′34″
73°23′34″
-
30° 54″
103°24′28″
(24′28″=23′88 ″)
试一试
课本P84习题A组第1题
(二)互余和互补(1)
1
2
A
B
C
O
已知∠AOB是直角, ∠1与∠2的和是多少度?
∠1 + ∠2= 90°
如果∠1 +∠2= 90°,那么我们就称∠1与∠2互为余角,简称互余.
其中∠1( ∠2 )叫做∠2( ∠1 )的余角
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
(二)互余和互补(2)
已知∠AOB是平角, ∠1与∠2的和是多少度?
∠1 + ∠2= 180°
如果∠1 +∠2= 180°,那么我们就称∠1与∠2互为补角,简称互补.
其中∠1( ∠2 )叫做∠2( ∠1 )的补角
C
B
A
O
2
1
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x
90° x
180° x
试一试
想一想:1、钝角有余角吗?
没有
2、直角有余角吗?
没有
3、同一个角的补角比它的
余角大多少度?
90°
1、90度的角叫余角,180度的角叫补角( )
3、如果一个角有补角,那么这个角一定是钝角( )
5、互补的两个角不可能相等。 ( )
4、钝角没有余角,但一定有补角。( )
6、互余的两个角一定都是锐角,两个锐角一定互余.
( )
2、若∠1 + ∠2+ ∠3 =90 °,则∠1 ,∠2, ∠3 互余。 ( )
7、如果 ( )
辨一辨
(三)余角和补角的性质
探究1:
C
D
2
1
3
O
A
B
如图:已知∠1与 ∠2互余, ∠3与 ∠2互余,那么∠1与 ∠3有什么关系?为什么?
相等 ∵ ∠1与 ∠2互余, ∠3与 ∠2互余
∴ ∠1 + ∠2 =90 °
∠3 + ∠2 =90 °
∴ ∠1 = 90°-∠2
∠3 = 90°-∠2
∴ ∠1 = ∠3
同角的余角相等。
C
A
B
D
1
2
3
4
探究2 已知:A、D、B在同一直线上,DC⊥AB,∠1 =∠2
则∠3、∠4关系如何?为什么?
分析:因为DC⊥AB (已知)
所以∠ADC=∠BDC = 。
所以∠1+ ∠3 = °移项得∠3= 。
∠2+ ∠4 = °移项得∠4= 。
因为∠1 =∠2 所以∠3 ∠4
90°
90
90 °-∠1
90
90 °-∠2
=
同角(或等角)的补角 .
同角(或等角)的余角相等 .
相等
余角的性质
你能用数学语言说明一下吗?
补角的性质
课本P83 练习题2
如图O是直线AB上一点,OE平分∠AOC,OD平分∠BOC,那么图中共有:
几对相等的角
(2) 几对互余的角
(3)几对互补的角
解: 相等的角2对: ∠1 = ∠2 , ∠3= ∠4
互余的角4对: ∠2与∠3, ∠1与 ∠4 ∠1与 ∠3, ∠2 与∠4
互补的角5对: ∠1与∠BOE, ∠4与∠AOD, ∠AOC与∠BOC,∠2 与BOE, ∠3与∠AOD
A
B
E
C
D
1
2
3
4
O
三、拓展提高
总结收获
畅谈体会
LOVE
2、余角、补角的概念:
3、余角、补角的性质:
谈谈你的收获?
1、角的和差计算
互余的角 互补的角
数量关系
对应图形
性质
C
D
E
N
A
O
B
M
1+ 2=90°
1+ 2=180°
同角(等角)的余角相等
同角(等角)的补角相等
四、家庭作业
练习题P63--65
一个角的余角是这个角的2倍,求这个角。
例题欣赏
解:设这个角为x °,则它的余角为 。
由题意可列方程 。
解得 。
答:这个角为 。
分析:用代数里设未知数列方程的方法来解
几何问题,是一种常见的解题思路。不妨你来试
一试吧!
(2x)°
X+2x=90
x=30
30 °
解:设这个角为x °,则它的余角为 。
由题意可列方程 。
解得 。
答:这个角为 。
(90-x)°
90-x=2x
x=30
30 °
方法二
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
