平行四边形的性质(第一课时)
文档属性
| 名称 | 平行四边形的性质(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-11 14:55:55 | ||
图片预览



文档简介
(共27张PPT)
人教版数学教材八年级下
19.1.1平行四边形的性质(第一课时)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯
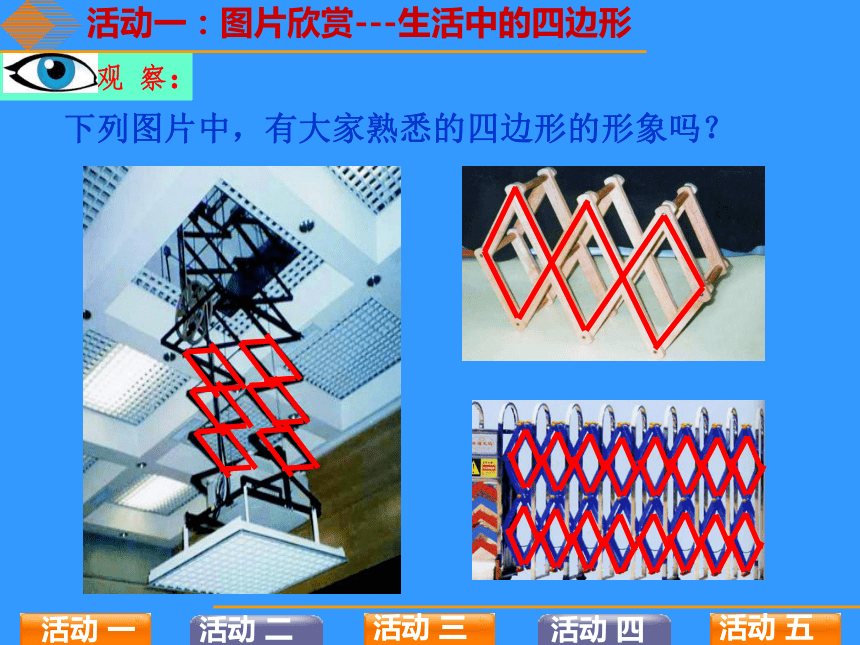
下列图片中,有大家熟悉的四边形的形象吗?
观 察:
活动一:图片欣赏---生活中的四边形
活动 一
活动 二
活动 三
活动 四
活动 五
退出
上页
下页
活动一
你能用手中一对全等的三角形纸片拼出几个平行四边形?
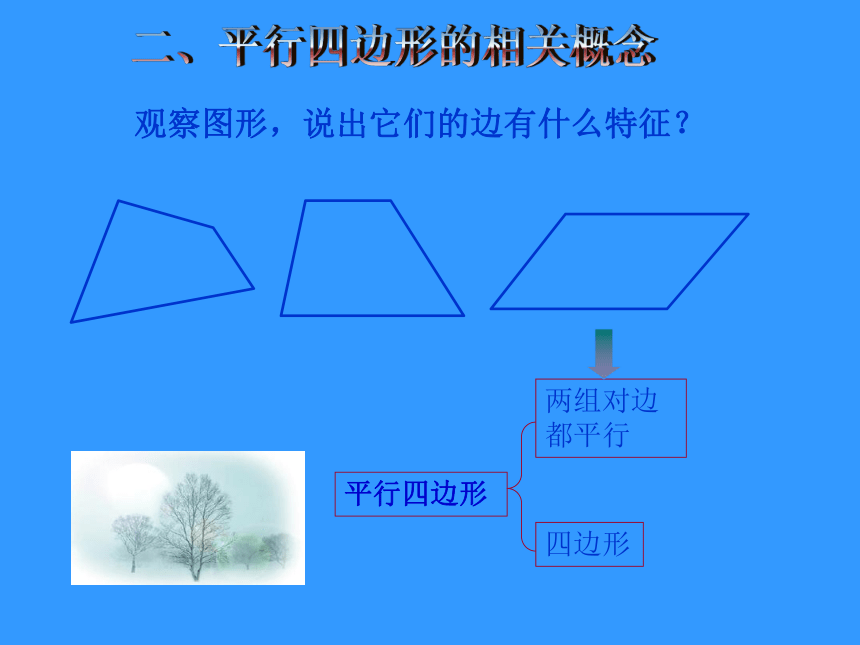
四边形
两组对边都平行
平行四边形
观察图形,说出它们的边有什么特征?
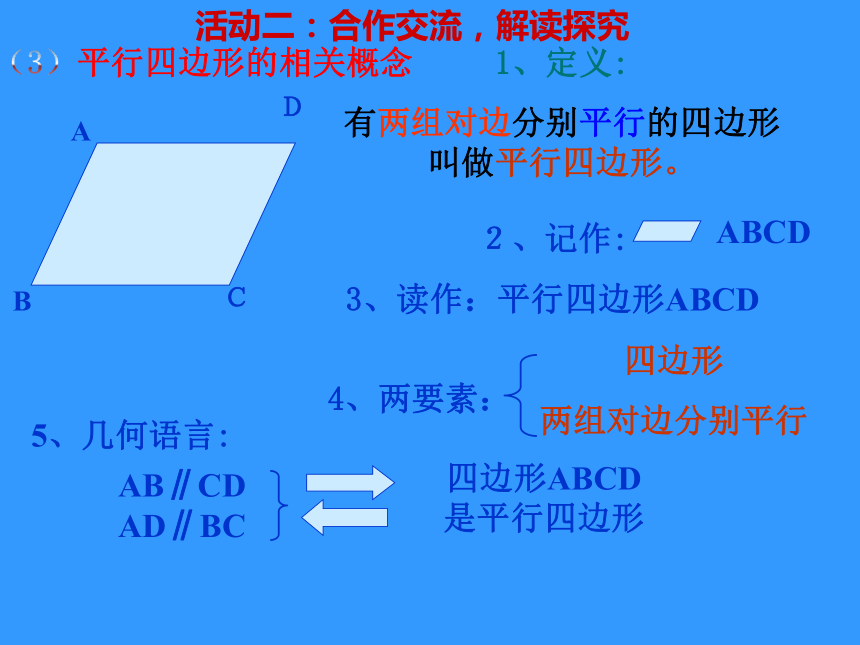
1、定义:
有两组对边分别平行的四边形 叫做平行四边形。
2、记作:
5、几何语言:
4、两要素:
A
B
D
C
四边形ABCD是平行四边形
ABCD
四边形
两组对边分别平行
AB∥CD AD∥BC
3、读作:平行四边形ABCD
活动二:合作交流,解读探究
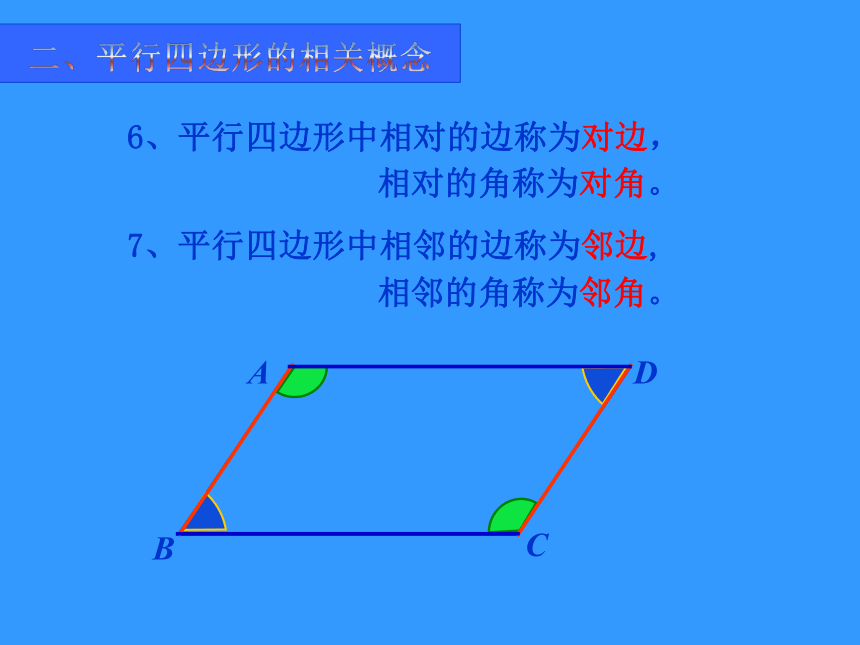
6、平行四边形中相对的边称为对边,
7、平行四边形中相邻的边称为邻边,
A
B
C
D
相邻的角称为邻角。
相对的角称为对角。
活动三:猜想、观察、探索
根据定义画一个平行四边形,观察这个四边形,除了 “两组对边分别平行”以外,它还有其它什么样结论?
A
B
C
D
A
B
C
D
(1)画一画
平行四边形的边、角
有怎样的数量关系?
活动三:猜想、观察、探索
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
用你以前所学的知识证明猜想.
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
活动三:猜想、观察、探索
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形性质1: 平行四边形的对边平行且相等。
平行四边形性质2: 平行四边形的对角相等,邻角互补
用符号语言表示:如图
A
B
C
D
ABCD
AD∥ BC AB∥ DC
AD=BC AB=DC
∠ A=∠ C ∠ B=∠ D
∠ A+ ∠ B=1800, ∠ B+ ∠ C=1800
活动三:猜想、观察、探索
3cm
A
B
D
C
5cm
4cm
3.求如图所示的四边形ABCD的面积.
3cm
活动 6
A
B
D
C
E
9cm
5cm
4.如图所示,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
活动 7
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
如图所示,用一对全等三角形拼出的这个四边形为什么是平行四边形呢?请说明理由.
A
B
C
D
A
B
C
D
如果已知平行四边形一个内角的度数,
能确定其他三个内角的度数吗?说说你的理由。
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C, ∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴ 其他三条边各长多少?
例2:有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
四边形ABCD是平行四边形
∠B= ∠ D
AD=BC=80cm
∠B=60°
∠D=60°
DE=AD-AE
AE=60cm
DE=20cm
AE∥BC
AB∥CF
解:
活动8:学以致用
2. ABCD的周长为12cm,AD=7cm
BC= ;CD= .
(2)随堂练习:
A
D
B
C
1.在 ABCD 中,AD=40,CD=30,
∠B=60°则BC= 40 ;AB=
∠A= , ∠C= , ∠D=
30
120°
120°
60°
7cm
5cm
3.在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
120°
40°
4 . ABCD中, ∠1=∠2,AB=5,BC=9,则ED= ,
△ABE是 三角形.
E
1
3
2
9
5
4
等腰
学习了本节课你有哪些收获?
退出
上页
下页
课堂回顾:
1:定义:两组对边分别平行的四边形叫做平行四边形.
2:性质:平行四边形的对边平行。
平行四边形的对边相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3:性质的运用
本课小结
定 义
表示方法
性 质
两组对边分别平行的四边形叫做 平 行 四边形。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”
平行四边形的对边相等,对角相等, 相邻两角互补.
活动五:课堂小结
知识与技能:
1、平行四边形的定义:两组对边分别
平行的四边形叫做平行四边形.
2、平行四边形的性质: 平行四边形的
对边平行且相等;平行四边形的对
角相等.
数学思想与方法:
1、“猜想——验证——证明”的科
学研究方法.
2、转化的数学思想.
感悟与收获
1.在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
3.如图,在 ABCD中,∠B的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
(第3题)
22
10cm,5cm
2
10
10
教材 90页 1、2题,
教材91页的第6题
作业:
人教版数学教材八年级下
19.1.1平行四边形的性质(第一课时)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
-------毕达哥拉斯
下列图片中,有大家熟悉的四边形的形象吗?
观 察:
活动一:图片欣赏---生活中的四边形
活动 一
活动 二
活动 三
活动 四
活动 五
退出
上页
下页
活动一
你能用手中一对全等的三角形纸片拼出几个平行四边形?
四边形
两组对边都平行
平行四边形
观察图形,说出它们的边有什么特征?
1、定义:
有两组对边分别平行的四边形 叫做平行四边形。
2、记作:
5、几何语言:
4、两要素:
A
B
D
C
四边形ABCD是平行四边形
ABCD
四边形
两组对边分别平行
AB∥CD AD∥BC
3、读作:平行四边形ABCD
活动二:合作交流,解读探究
6、平行四边形中相对的边称为对边,
7、平行四边形中相邻的边称为邻边,
A
B
C
D
相邻的角称为邻角。
相对的角称为对角。
活动三:猜想、观察、探索
根据定义画一个平行四边形,观察这个四边形,除了 “两组对边分别平行”以外,它还有其它什么样结论?
A
B
C
D
A
B
C
D
(1)画一画
平行四边形的边、角
有怎样的数量关系?
活动三:猜想、观察、探索
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
用你以前所学的知识证明猜想.
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
活动三:猜想、观察、探索
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形性质1: 平行四边形的对边平行且相等。
平行四边形性质2: 平行四边形的对角相等,邻角互补
用符号语言表示:如图
A
B
C
D
ABCD
AD∥ BC AB∥ DC
AD=BC AB=DC
∠ A=∠ C ∠ B=∠ D
∠ A+ ∠ B=1800, ∠ B+ ∠ C=1800
活动三:猜想、观察、探索
3cm
A
B
D
C
5cm
4cm
3.求如图所示的四边形ABCD的面积.
3cm
活动 6
A
B
D
C
E
9cm
5cm
4.如图所示,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
活动 7
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
如图所示,用一对全等三角形拼出的这个四边形为什么是平行四边形呢?请说明理由.
A
B
C
D
A
B
C
D
如果已知平行四边形一个内角的度数,
能确定其他三个内角的度数吗?说说你的理由。
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C, ∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴ 其他三条边各长多少?
例2:有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
四边形ABCD是平行四边形
∠B= ∠ D
AD=BC=80cm
∠B=60°
∠D=60°
DE=AD-AE
AE=60cm
DE=20cm
AE∥BC
AB∥CF
解:
活动8:学以致用
2. ABCD的周长为12cm,AD=7cm
BC= ;CD= .
(2)随堂练习:
A
D
B
C
1.在 ABCD 中,AD=40,CD=30,
∠B=60°则BC= 40 ;AB=
∠A= , ∠C= , ∠D=
30
120°
120°
60°
7cm
5cm
3.在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
120°
40°
4 . ABCD中, ∠1=∠2,AB=5,BC=9,则ED= ,
△ABE是 三角形.
E
1
3
2
9
5
4
等腰
学习了本节课你有哪些收获?
退出
上页
下页
课堂回顾:
1:定义:两组对边分别平行的四边形叫做平行四边形.
2:性质:平行四边形的对边平行。
平行四边形的对边相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3:性质的运用
本课小结
定 义
表示方法
性 质
两组对边分别平行的四边形叫做 平 行 四边形。
平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”
平行四边形的对边相等,对角相等, 相邻两角互补.
活动五:课堂小结
知识与技能:
1、平行四边形的定义:两组对边分别
平行的四边形叫做平行四边形.
2、平行四边形的性质: 平行四边形的
对边平行且相等;平行四边形的对
角相等.
数学思想与方法:
1、“猜想——验证——证明”的科
学研究方法.
2、转化的数学思想.
感悟与收获
1.在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
2. ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3. ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
3.如图,在 ABCD中,∠B的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
(第3题)
22
10cm,5cm
2
10
10
教材 90页 1、2题,
教材91页的第6题
作业:
