10.1.4 概率的基本性质课件(共15张PPT)
文档属性
| 名称 | 10.1.4 概率的基本性质课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-17 23:23:07 | ||
图片预览






文档简介
第10章 概 率
10.1.4 概率的基本性质
高中数学人教A版(2019)必修 第二册
概率的基本性质(1)(2)(5)
性质(1)(2)(5)
一般地,概率有如下性质:
性质1
对任意的事件A,都有P(A)≥0
性质2
必然事件的概率为1,不可能事件的概率为0,即P(Ω)=1,P(?)=0
性质5
如果A?B,
那么P(A)≤P(B)
?
概率是[0,1]之间的一个常数,不随事件结果的改变而改变,它是频率的科学抽象. .
探究新知
概率的基本性质(1)(2)(5)
一般地,对于事件A和事件B,如果A?B ,即事件A发生,事件B一定发生,那么事件A的概率不超过事件B的概率
?
在古典概型中,对于事件A和事件B,如果A?B ,那么n(A)≤n(B),
?
由性质5可得,对于任意事件A,因为? ??A ??Ω,所以0≤P(A) ≤1
?
即????(????)????(????)≤????(????)????(????),即P(A)≤P(B)
?
概率的基本性质(1)(2)(5)
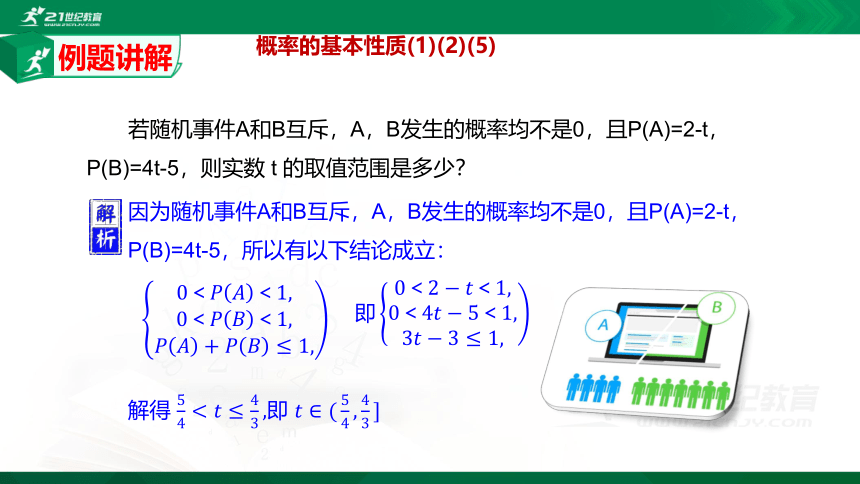
若随机事件A和B互斥,A,B发生的概率均不是0,且P(A)=2-t,P(B)=4t-5,则实数 t 的取值范围是多少?
因为随机事件A和B互斥,A,B发生的概率均不是0,且P(A)=2-t,P(B)=4t-5,所以有以下结论成立:
0<????????<1,0<????????<1,????????+????????≤1,
?
即0<2?????<1,0<4?????5<1,3?????3≤1,
?
解得 54?
例题讲解
互斥事件的概率加法公式(性质3)
性质3
如果事件A和事件B互斥,那么P(A∪B)=P(A)+P(B)
互斥事件的概率加法公式应用的前提是“事件A和事件B互斥”,否则不可以用这个公式. 实际上,对于事件A,B,有P(A∪B)≤P(A)+P(B),只有当事件A和事件B互斥时,等号才成立.
互斥事件的概率加法公式可以推广到多个事件的情况,如果事件A1,A2,…,Am两两互斥,那么事件A1∪A2∪…∪Am发生的概率等于这m个事件分别发生的概率之和,即P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am)
探究新知
互斥事件的概率加法公式(性质3)
下列四种说法:
①对立事件一定是互斥事件
②若A,B为两个事件,则P(A∪B)=P(A)+P(B)
③若事件A,B,C两两互斥,则P(A)+P(B)+P(C)=1
④若事件A,B满足P(A)+P(B)=1,则A,B是对立事件
其中错误的是_________.
对立事件一定是互斥事件,且对立的两个事件概率之和为1,但互斥事件的概率之和不一定是1,所以错误的是②③④
②③④
例题讲解
对立事件的概率(性质4)
性质4
因为事件A和事件B互为对立事件,所以它们的和事件A∪B为必然事件,即P(A∪B)=1.由性质3,得P(A)+P(B)=P(A∪B)=1.
如果事件A和事件B为对立事件,那么它们的概率之和为1
性质4
性质4适用于一个事件的概率不容易求出,但其对立事件的概率易于求出的情况.
性质4的前提是“事件A和事件B为对立事件”
探究新知
概率的一般加法公式(性质6)
性质6
设A,B是一个随机试验中的两个事件,有
概率的一般加法公式与互斥事件的概率加法公式在限制条件上有区别:在公式P(A)+P(B)=P(A∪B)中,事件A,B是互斥事件;在公式P(A∪B)=P(A)+P(B)-P(A∩B)中,事件A,B可以是互斥事件,也可以不是互斥事件
P(A∪B)=P(A)+P(B)-P(A∩B)
探究新知
概率的一般加法公式(性质6)
用集合知识理解概率的加法公式:
在集合中可知,
Card(A∪B)=Card(B)+Card(B)-Card(A∩B).
而互斥是这个公式的特殊情况.
一般事件的概率加法公式,即P(A∪B)=P(A)+P(B)-P(A∩B). 当A与B互斥时,A∩B=?,P(?)=0,可见互斥事件的概率加法公式满足一般事件的概率加法公式.
不能区分事件是否互斥而做错
抛掷一枚质地均匀的骰子,向上一面出现1,2,3,4,5,6的概率都是六分之一,记事件A为“出现奇数点”,事件B为“向上的点数不超过3”,求P(A∪B)
P(A∪B)=P(A)+P(B)= 16×3+16×3=1
?
记事件“出现1点” “出现2点” “出现3点” “出现5点”分别为M,N,P,Q,由题意可知这4个事件彼此互斥.
错解中认为事件A和事件B是互斥事件,所以得出P(A∪B)=1
所以P(A∪B)=P(M)+P(N)+P(P)+P(Q)= 16×4=23
?
课堂练习
某战士射击一次,击中环数大于7的概率是0.6,击中环数是6或7或8的概率相等,且和为0.3,求该战士射击一次击中环数大于5的概率.
记“击中6环”为事件A,“击中7环”为事件B,“击中7环以上”位事件C,事件A,B,C彼此互斥,且易知P(A)=P(B)=0.3÷3=0.1,P(C)=0.6,记“击中5环以上”为事件D,故P(D)=P(A∪B∪C)=0.1+0.1+0.6=0.8
课堂练习
对立事件的概率公式使用错误
某商店月收入(单位:元)在下列范围内的概率如表所示:
记这个商店月收入在[1000,1500), [1500,2000), [2000,2500), [2500,3000)元范围内的事件分别为A,B,C,D,因为A,B,C,D互斥,且P(A)+P(B)+P(C)+P(D),
所以P(B∪C∪D)=0.67-P(A)=0.55
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入
[1000,1500)
[1500,2000)
[2000,2500)
[2500,3000)
概率
0.12
????
????
0.14
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入
[1000,1500)
[1500,2000)
[2000,2500)
[2500,3000)
概率
0.12
0.14
已知月收入在[1000,3000)元范围内的概率为0.67,求月收入在[1500,3000)元范围内的概率
课堂练习
卢老师和小黄豆下棋,和棋的概率是 0.5,小黄豆获胜的概率是0.3,求:
(1)卢老师获胜的概率 (2)卢老师不输的概率
(1)“卢老师获胜”可看做是“和棋”或“小黄豆获胜”的对立事
件,所以卢老师获胜的概率为1-0.5-0.3=0.2
(2)“卢老师不输”可看做是“和棋”或“小老师获胜”这两个互
斥事件的和事件,所以卢老师获胜的概率为0.5+0.2=0.7
课堂练习
谢谢聆听
10.1.4 概率的基本性质
高中数学人教A版(2019)必修 第二册
概率的基本性质(1)(2)(5)
性质(1)(2)(5)
一般地,概率有如下性质:
性质1
对任意的事件A,都有P(A)≥0
性质2
必然事件的概率为1,不可能事件的概率为0,即P(Ω)=1,P(?)=0
性质5
如果A?B,
那么P(A)≤P(B)
?
概率是[0,1]之间的一个常数,不随事件结果的改变而改变,它是频率的科学抽象. .
探究新知
概率的基本性质(1)(2)(5)
一般地,对于事件A和事件B,如果A?B ,即事件A发生,事件B一定发生,那么事件A的概率不超过事件B的概率
?
在古典概型中,对于事件A和事件B,如果A?B ,那么n(A)≤n(B),
?
由性质5可得,对于任意事件A,因为? ??A ??Ω,所以0≤P(A) ≤1
?
即????(????)????(????)≤????(????)????(????),即P(A)≤P(B)
?
概率的基本性质(1)(2)(5)
若随机事件A和B互斥,A,B发生的概率均不是0,且P(A)=2-t,P(B)=4t-5,则实数 t 的取值范围是多少?
因为随机事件A和B互斥,A,B发生的概率均不是0,且P(A)=2-t,P(B)=4t-5,所以有以下结论成立:
0<????????<1,0<????????<1,????????+????????≤1,
?
即0<2?????<1,0<4?????5<1,3?????3≤1,
?
解得 54?
例题讲解
互斥事件的概率加法公式(性质3)
性质3
如果事件A和事件B互斥,那么P(A∪B)=P(A)+P(B)
互斥事件的概率加法公式应用的前提是“事件A和事件B互斥”,否则不可以用这个公式. 实际上,对于事件A,B,有P(A∪B)≤P(A)+P(B),只有当事件A和事件B互斥时,等号才成立.
互斥事件的概率加法公式可以推广到多个事件的情况,如果事件A1,A2,…,Am两两互斥,那么事件A1∪A2∪…∪Am发生的概率等于这m个事件分别发生的概率之和,即P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am)
探究新知
互斥事件的概率加法公式(性质3)
下列四种说法:
①对立事件一定是互斥事件
②若A,B为两个事件,则P(A∪B)=P(A)+P(B)
③若事件A,B,C两两互斥,则P(A)+P(B)+P(C)=1
④若事件A,B满足P(A)+P(B)=1,则A,B是对立事件
其中错误的是_________.
对立事件一定是互斥事件,且对立的两个事件概率之和为1,但互斥事件的概率之和不一定是1,所以错误的是②③④
②③④
例题讲解
对立事件的概率(性质4)
性质4
因为事件A和事件B互为对立事件,所以它们的和事件A∪B为必然事件,即P(A∪B)=1.由性质3,得P(A)+P(B)=P(A∪B)=1.
如果事件A和事件B为对立事件,那么它们的概率之和为1
性质4
性质4适用于一个事件的概率不容易求出,但其对立事件的概率易于求出的情况.
性质4的前提是“事件A和事件B为对立事件”
探究新知
概率的一般加法公式(性质6)
性质6
设A,B是一个随机试验中的两个事件,有
概率的一般加法公式与互斥事件的概率加法公式在限制条件上有区别:在公式P(A)+P(B)=P(A∪B)中,事件A,B是互斥事件;在公式P(A∪B)=P(A)+P(B)-P(A∩B)中,事件A,B可以是互斥事件,也可以不是互斥事件
P(A∪B)=P(A)+P(B)-P(A∩B)
探究新知
概率的一般加法公式(性质6)
用集合知识理解概率的加法公式:
在集合中可知,
Card(A∪B)=Card(B)+Card(B)-Card(A∩B).
而互斥是这个公式的特殊情况.
一般事件的概率加法公式,即P(A∪B)=P(A)+P(B)-P(A∩B). 当A与B互斥时,A∩B=?,P(?)=0,可见互斥事件的概率加法公式满足一般事件的概率加法公式.
不能区分事件是否互斥而做错
抛掷一枚质地均匀的骰子,向上一面出现1,2,3,4,5,6的概率都是六分之一,记事件A为“出现奇数点”,事件B为“向上的点数不超过3”,求P(A∪B)
P(A∪B)=P(A)+P(B)= 16×3+16×3=1
?
记事件“出现1点” “出现2点” “出现3点” “出现5点”分别为M,N,P,Q,由题意可知这4个事件彼此互斥.
错解中认为事件A和事件B是互斥事件,所以得出P(A∪B)=1
所以P(A∪B)=P(M)+P(N)+P(P)+P(Q)= 16×4=23
?
课堂练习
某战士射击一次,击中环数大于7的概率是0.6,击中环数是6或7或8的概率相等,且和为0.3,求该战士射击一次击中环数大于5的概率.
记“击中6环”为事件A,“击中7环”为事件B,“击中7环以上”位事件C,事件A,B,C彼此互斥,且易知P(A)=P(B)=0.3÷3=0.1,P(C)=0.6,记“击中5环以上”为事件D,故P(D)=P(A∪B∪C)=0.1+0.1+0.6=0.8
课堂练习
对立事件的概率公式使用错误
某商店月收入(单位:元)在下列范围内的概率如表所示:
记这个商店月收入在[1000,1500), [1500,2000), [2000,2500), [2500,3000)元范围内的事件分别为A,B,C,D,因为A,B,C,D互斥,且P(A)+P(B)+P(C)+P(D),
所以P(B∪C∪D)=0.67-P(A)=0.55
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入
[1000,1500)
[1500,2000)
[2000,2500)
[2500,3000)
概率
0.12
????
????
0.14
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入
[1000,1500)
[1500,2000)
[2000,2500)
[2500,3000)
概率
0.12
0.14
已知月收入在[1000,3000)元范围内的概率为0.67,求月收入在[1500,3000)元范围内的概率
课堂练习
卢老师和小黄豆下棋,和棋的概率是 0.5,小黄豆获胜的概率是0.3,求:
(1)卢老师获胜的概率 (2)卢老师不输的概率
(1)“卢老师获胜”可看做是“和棋”或“小黄豆获胜”的对立事
件,所以卢老师获胜的概率为1-0.5-0.3=0.2
(2)“卢老师不输”可看做是“和棋”或“小老师获胜”这两个互
斥事件的和事件,所以卢老师获胜的概率为0.5+0.2=0.7
课堂练习
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
