2020-2021学年湘教新版八年级下册数学期末冲刺试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学期末冲刺试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 357.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 08:06:55 | ||
图片预览

文档简介
2020-2021学年湘教新版八年级下册数学期末冲刺试题
一.选择题(共10小题,满分40分,每小题4分)
1.下列手机手势解锁图案中,是中心对称图形的是( )
A.
B.
C.
D.
2.如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为( )
A.1
B.2
C.3
D.4
3.下列对菱形的描述错误的是( )
A.菱形的四条边都相等
B.对角线相等的平行四边形是菱形
C.菱形的对角线互相垂直
D.邻边相等的平行四边形是菱形
4.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.8
B.7
C.6
D.5
5.在正方形ABCD的外侧,作等边三角形ADE,则∠CBE的度数为( )
A.80°
B.75°
C.70°
D.65°
6.在平面直角坐标系中,点P(﹣x2﹣1,2)的位置在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.在平面直角坐标系中,点A的坐标为(﹣2,10),点B与点A关于x轴对称,则点B的坐标为( )
A.(2,10)
B.(10,2)
C.(﹣2,﹣10)
D.(10,﹣2)
8.函数y=中自变量x的取值范围是( )
A.x≥﹣2且x≠1
B.x≥﹣2
C.x≠1
D.﹣2≤x<1
9.一次函数y=﹣kx﹣k的图象可能是( )
A.
B.
C.
D.
10.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③
B.①②④
C.①③④
D.①②③④
二.填空题(共8小题,满分32分,每小题4分)
11.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是
.
12.如图,在Rt△ABC中,∠A=90°,∠ACB=30°,BD平分∠ABC,交AC于点D,CD=4,则点D到BC的距离是
.
13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、13,第五组的频率是0.1,那么第六组的频数是
.
14.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=58°,则∠BAD=
.
15.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
.
16.一次函数y=﹣2x﹣1的图象与x轴、y轴分别交于点A、B,则△AOB的面积是
.
17.如图,在矩形ABCD中,对角线AC,BD交于点O,过点C作CE⊥CA,交BD的延长线于点E,若AB=2,BC=4,则DE的长为
.
18.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.若AB=,BD=2,则OE的长为
.
三.解答题(共8小题,满分78分)
19.已知y是x的一次函数,且当x=﹣4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的解析式;
(2)求当﹣3<y≤1时,自变量x取值范围.
20.平面直角坐标系中,有一个点P(a﹣1,5﹣a)
(1)若点P在x轴上,则a=
则此时点P的坐标为
;
(2)若点P是第一象限的整点(横纵坐标都是整数的点,称为整点),则这样的整点有几个?并求出这些整点的坐标?
(3)点P可能在第三象限吗?为什么?
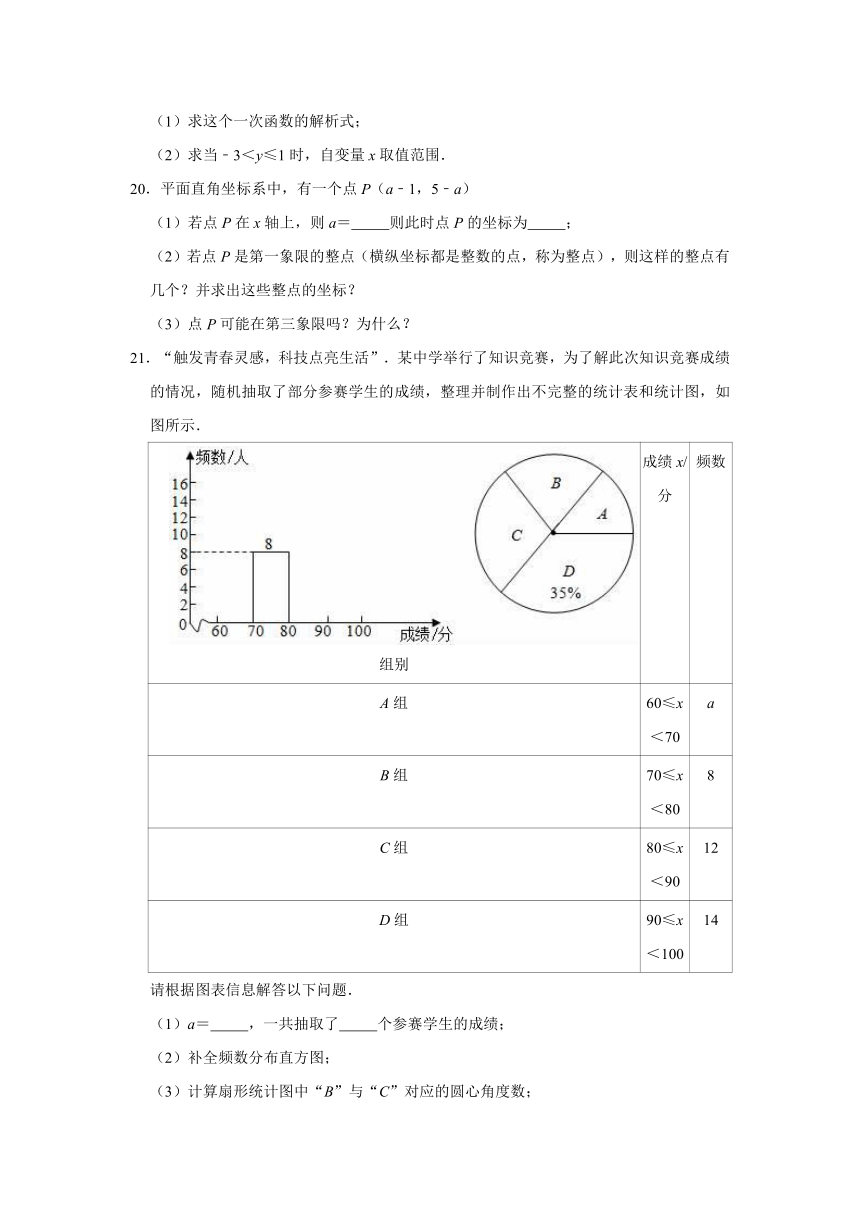
21.“触发青春灵感,科技点亮生活”.某中学举行了知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出不完整的统计表和统计图,如图所示.
组别
成绩x/分
频数
A组
60≤x<70
a
B组
70≤x<80
8
C组
80≤x<90
12
D组
90≤x<100
14
请根据图表信息解答以下问题.
(1)a=
,一共抽取了
个参赛学生的成绩;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”与“C”对应的圆心角度数;
(4)若学校为成绩在80分以上(包括80分)的学生颁发优秀证书,则抽取学生成绩为“优秀”的人数占所抽取学生的百分比是多少?
22.已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:AF=CE.
23.如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
24.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
25.“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系式如图中折线段AB﹣BC﹣CD所示.
(1)小丽与小明出发
min相遇;
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少?
②计算出点C的坐标,并解释点C的实际意义.
26.长方形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
(1)如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B′点,求B′点的坐标.
(2)求折痕CM所在直线的解析式.
(3)在x轴上是否能找到一点P,使△B′CP的面积为13?若存在,直接写出点P的坐标?若不存在,请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:A、不是中心对称图形;
B、是中心对称图形;
C、不是中心对称图形;
D、不是中心对称图形.
故选:B.
2.解:∵正方形EFGH的面积=正方形ABCD的面积﹣4S△ABE=102﹣4×24=4,
∴正方形EFGH的边长=2,
故选:B.
3.解:A、∵菱形的四条边都相等,
∴选项A不符合题意;
B、∵对角线相等的平行四边形是矩形,
∴选项B符合题意;
C、∵菱形的对角线互相垂直平分,
∴选项C不符合题意;
D、∵邻边相等的平行四边形形是菱形,
∴选项D不符合题意;
故选:B.
4.解:连接DN,
∵点E,F分别为DM,MN的中点,
∴EF是△MND的中位线,
∴EF=DN,
∵点M,N分别为线段BC,AB上的动点,
∴当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为:×10=5,
故选:D.
5.解:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=AD,
∵△ADE是等边三角形,
∴∠EAD=60°,AE=AD,
∴∠BAE=150°,AB=AE,
∴∠ABE=∠AEB=15°,
∴∠CBE=90°﹣15°=75°,
故选:B.
6.解:∵﹣x2﹣1<0,2>0,故点在第二象限,
故选:B.
7.解:∵点A坐标为(﹣2,10),点B与点A关于x轴对称,
∴点B的坐标为:(﹣2,﹣10).
故选:C.
8.解:根据二次根式有意义,分式有意义得:x+2≥0且x﹣1≠0,
解得:x≥﹣2且x≠1.
故选:A.
9.解:当k>0时,﹣k<0,此时函数图象经过二、三、四象限,B选项符合条件;
当k<0时,﹣k>0,此时函数图象经过一、二、三象限,无选项符合条件.
故选:B.
10.解:①∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得,解得,
∴直线l1:y=2x+4,
又∵直线l2:y=﹣x+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确,符合题意;
③把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③错误,不符合题意;
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:∵AD平分∠CAB,∠CAD=20°,
∴∠CAB=2∠CAD=40°,
∵∠ACB=90°,
∴∠B=90°﹣40°=50°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠EDB=90°﹣50°=40°,
故答案为:40°.
12.解:∵Rt△ABC中,∠ACB=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠DBC=∠ACB,
∴BD=CD=4,
在Rt△ABD中,∵∠ABD=30°,
∴AD=BD=×4=2,
过点D作DE⊥BC于点E,
则DE=AD=2,
故答案为:2.
13.解:根据题意,得:第一组到第四组的频率和是=0.875,
又∵第五组的频率是0.1,
∴第六组的频率为1﹣(0.875+0.1)=0.025,
∴第六组的频数为:40×0.025=1.
故答案为:1.
14.解:∵AE⊥BC于点E,AF⊥CD于点F,
∴∠AEC=∠AFC=90°,
又∵∠EAF=58°,
∴∠C=360°﹣58°﹣90°﹣90°=122°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠C=122°.
故答案为:122°.
15.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
16.解:当x=0时,y=﹣2×0﹣1=﹣1,
∴点B的坐标为(0,﹣1),
∴OB=1;
当y=0时,﹣2x﹣1=0,解得:x=﹣,
∴点A的坐标为(﹣,0),
∴OA=.
∴S△AOB=OA?OB=.
故答案为:.
17.解:如图,过点D作DH⊥AC于H,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∵AB=2,BC=4,
∴AC===2,
∴OD=OC=,
∵S△ADC=×AD×DC=×AC×DH,
∴2×4=2×DH,
∴DH=,
∴OH===,
∴HC=﹣=,
∵CE⊥CA,DH⊥CA,
∴CE∥DH,
∴,
∴,
∴DE=.
18.解:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA===2,
∴OE=OA=2,
故答案为:2.
三.解答题(共8小题,满分78分)
19.解:(1)设一次函数解析式为y=kx+b(k≠0),
把x=﹣4,y=9;x=6,y=﹣1代入得:,
解得:,
则一次函数解析式为y=﹣x+5;
(2)y=﹣x+5,
∵k=﹣1<0,
∴y随x的增大而减小,
当y=﹣3时,﹣3=﹣x+5,即x=8,
当y=1时,1=﹣x+5,即x=4,
则当﹣3<y≤1时,自变量x的范围是4≤x<8.
20.解:(1)因为点P在x轴上,可得:5﹣a=0,
解得:a=5,
所以点P的坐标为(4,0);
故答案为:5;(4,0)
(2)因为点P是第一象限,可得:,
解得:1<a<5,
因为是整数,
所以a可以取2,3,4,
此时坐标分别为(1,3),(2,2),(3,1);
(3)若点P在第三象限,可得:,
此不等式组无解,
所以点P不可能在第三象限.
21.解:(1)14÷35%=40(人),a=40﹣14﹣12﹣8=6(人),
故答案为:6,40;
(2)补全频数分布直方图如下:
(3)“B组”所对应的圆心角的度数为:360°×=72°,
“C组”所对应的圆心角的度数为:360°×=108°,
(4)×100%=65%,
答:抽取学生成绩为“优秀”的人数占所抽取学生的百分比是65%.
22.证明:∵DE=BF,
∴DE+EF=BF+EF;
∴DF=BE;
在Rt△ADF和Rt△BCE中
,
∴Rt△ADF≌Rt△BCE,
∴AF=CE.
23.(1)证明∵E为AD的中点,
∴DE=AE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠EDC=∠EAF,
在△DEC和△AEF中,,
∴△DEC≌△AEF(AAS),
∴DC=FA,
∵AD=2AB,
∴AB=DE=EA=FA,
∴FB=AD;
(2)解:∵四边形ABCD是平行四边形,
∴DA∥CB,
∴∠CBF=∠DAF=70°,∠AEB=∠EBC,
又∵AE=AB,
∴∠AEB=∠ABE,
∴∠EBC=∠ABE=35°.
24.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,
∴∠BAD=∠ABC,
∴2∠BAD=180°,∴∠BAD=90°,
∴四边形ABCD是正方形;
(2)证明:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,CO=AC,DO=BD,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,
∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH,
在△ECO和△FDO中,,
∴△ECO≌△FDO(ASA),
∴OE=OF.
25.解:(1)由图象可得小丽与小明出发30min相遇,
故答案为:30;
(2)①设小丽步行的速度为V1m/min,小明步行的速度为V2m/min,且V2>V1,
则,
解得:,
答:小丽步行的速度为80m/min,小明步行的速度为100m/min;
②解法一:设点C的坐标为(x,y),
则可得方程(100+80)(x﹣30)+80(67.5﹣x)=5400,
解得x=54,y=(100+80)(54﹣30)=4320m,
解法二:5400÷100=54,54×80=4320,
∴点C(54,4320),
点C表示:两人出发54min时,小明到达甲地,此时两人相距4320m.
26.解:(1)∵四边形ABCO为矩形,
∴CB=OA=10,AB=OC=6,
∵△CBM沿CM翻折后,点B落在x轴上,记作B′点,
∴CB′=CB=10,B′M=BM,
在Rt△OCB′中,OC=6,CB′=10,
∴OB′=8,
∴B′点的坐标为(8,0);
(2)设AM=t,则BM=B′M=6﹣t,
而AB′=OA﹣OB′=2,
在Rt△AB′M中,B′M2=B′A2+AM2,
即(6﹣t)2=22+t2,
解得t=,
∴M点的坐标为(10,),
设直线CM的解析式为y=kx+b,
把C(0,6)和M(10,)代入得,,解得,
∴直线CM的解析式为y=﹣x+6;
(3)存在,理由:
设点P的坐标为(x,0),
则△B′CP的面积=PB′×OC=|x﹣8|×6=13,
解得x=或,
故点P的坐标为(,0)或(,0).
一.选择题(共10小题,满分40分,每小题4分)
1.下列手机手势解锁图案中,是中心对称图形的是( )
A.
B.
C.
D.
2.如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为( )
A.1
B.2
C.3
D.4
3.下列对菱形的描述错误的是( )
A.菱形的四条边都相等
B.对角线相等的平行四边形是菱形
C.菱形的对角线互相垂直
D.邻边相等的平行四边形是菱形
4.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.8
B.7
C.6
D.5
5.在正方形ABCD的外侧,作等边三角形ADE,则∠CBE的度数为( )
A.80°
B.75°
C.70°
D.65°
6.在平面直角坐标系中,点P(﹣x2﹣1,2)的位置在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.在平面直角坐标系中,点A的坐标为(﹣2,10),点B与点A关于x轴对称,则点B的坐标为( )
A.(2,10)
B.(10,2)
C.(﹣2,﹣10)
D.(10,﹣2)
8.函数y=中自变量x的取值范围是( )
A.x≥﹣2且x≠1
B.x≥﹣2
C.x≠1
D.﹣2≤x<1
9.一次函数y=﹣kx﹣k的图象可能是( )
A.
B.
C.
D.
10.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③
B.①②④
C.①③④
D.①②③④
二.填空题(共8小题,满分32分,每小题4分)
11.如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交边BC于点D,过点D作DE⊥AB,垂足为E.若∠CAD=20°,则∠EDB的度数是
.
12.如图,在Rt△ABC中,∠A=90°,∠ACB=30°,BD平分∠ABC,交AC于点D,CD=4,则点D到BC的距离是
.
13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、13,第五组的频率是0.1,那么第六组的频数是
.
14.如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=58°,则∠BAD=
.
15.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
.
16.一次函数y=﹣2x﹣1的图象与x轴、y轴分别交于点A、B,则△AOB的面积是
.
17.如图,在矩形ABCD中,对角线AC,BD交于点O,过点C作CE⊥CA,交BD的延长线于点E,若AB=2,BC=4,则DE的长为
.
18.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.若AB=,BD=2,则OE的长为
.
三.解答题(共8小题,满分78分)
19.已知y是x的一次函数,且当x=﹣4时,y=9;当x=6时,y=﹣1.
(1)求这个一次函数的解析式;
(2)求当﹣3<y≤1时,自变量x取值范围.
20.平面直角坐标系中,有一个点P(a﹣1,5﹣a)
(1)若点P在x轴上,则a=
则此时点P的坐标为
;
(2)若点P是第一象限的整点(横纵坐标都是整数的点,称为整点),则这样的整点有几个?并求出这些整点的坐标?
(3)点P可能在第三象限吗?为什么?
21.“触发青春灵感,科技点亮生活”.某中学举行了知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出不完整的统计表和统计图,如图所示.
组别
成绩x/分
频数
A组
60≤x<70
a
B组
70≤x<80
8
C组
80≤x<90
12
D组
90≤x<100
14
请根据图表信息解答以下问题.
(1)a=
,一共抽取了
个参赛学生的成绩;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”与“C”对应的圆心角度数;
(4)若学校为成绩在80分以上(包括80分)的学生颁发优秀证书,则抽取学生成绩为“优秀”的人数占所抽取学生的百分比是多少?
22.已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:AF=CE.
23.如图,平行四边形ABCD中,AD=2AB,E为AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:FB=AD.
(2)若∠DAF=70°,求∠EBC的度数.
24.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形.
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
25.“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系式如图中折线段AB﹣BC﹣CD所示.
(1)小丽与小明出发
min相遇;
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少?
②计算出点C的坐标,并解释点C的实际意义.
26.长方形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.
(1)如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B′点,求B′点的坐标.
(2)求折痕CM所在直线的解析式.
(3)在x轴上是否能找到一点P,使△B′CP的面积为13?若存在,直接写出点P的坐标?若不存在,请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:A、不是中心对称图形;
B、是中心对称图形;
C、不是中心对称图形;
D、不是中心对称图形.
故选:B.
2.解:∵正方形EFGH的面积=正方形ABCD的面积﹣4S△ABE=102﹣4×24=4,
∴正方形EFGH的边长=2,
故选:B.
3.解:A、∵菱形的四条边都相等,
∴选项A不符合题意;
B、∵对角线相等的平行四边形是矩形,
∴选项B符合题意;
C、∵菱形的对角线互相垂直平分,
∴选项C不符合题意;
D、∵邻边相等的平行四边形形是菱形,
∴选项D不符合题意;
故选:B.
4.解:连接DN,
∵点E,F分别为DM,MN的中点,
∴EF是△MND的中位线,
∴EF=DN,
∵点M,N分别为线段BC,AB上的动点,
∴当点N与点B重合时,DN最大,此时DN==10,
∴EF长度的最大值为:×10=5,
故选:D.
5.解:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=AD,
∵△ADE是等边三角形,
∴∠EAD=60°,AE=AD,
∴∠BAE=150°,AB=AE,
∴∠ABE=∠AEB=15°,
∴∠CBE=90°﹣15°=75°,
故选:B.
6.解:∵﹣x2﹣1<0,2>0,故点在第二象限,
故选:B.
7.解:∵点A坐标为(﹣2,10),点B与点A关于x轴对称,
∴点B的坐标为:(﹣2,﹣10).
故选:C.
8.解:根据二次根式有意义,分式有意义得:x+2≥0且x﹣1≠0,
解得:x≥﹣2且x≠1.
故选:A.
9.解:当k>0时,﹣k<0,此时函数图象经过二、三、四象限,B选项符合条件;
当k<0时,﹣k>0,此时函数图象经过一、二、三象限,无选项符合条件.
故选:B.
10.解:①∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得,解得,
∴直线l1:y=2x+4,
又∵直线l2:y=﹣x+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确,符合题意;
③把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③错误,不符合题意;
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
11.解:∵AD平分∠CAB,∠CAD=20°,
∴∠CAB=2∠CAD=40°,
∵∠ACB=90°,
∴∠B=90°﹣40°=50°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠EDB=90°﹣50°=40°,
故答案为:40°.
12.解:∵Rt△ABC中,∠ACB=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠DBC=∠ACB,
∴BD=CD=4,
在Rt△ABD中,∵∠ABD=30°,
∴AD=BD=×4=2,
过点D作DE⊥BC于点E,
则DE=AD=2,
故答案为:2.
13.解:根据题意,得:第一组到第四组的频率和是=0.875,
又∵第五组的频率是0.1,
∴第六组的频率为1﹣(0.875+0.1)=0.025,
∴第六组的频数为:40×0.025=1.
故答案为:1.
14.解:∵AE⊥BC于点E,AF⊥CD于点F,
∴∠AEC=∠AFC=90°,
又∵∠EAF=58°,
∴∠C=360°﹣58°﹣90°﹣90°=122°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠C=122°.
故答案为:122°.
15.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
16.解:当x=0时,y=﹣2×0﹣1=﹣1,
∴点B的坐标为(0,﹣1),
∴OB=1;
当y=0时,﹣2x﹣1=0,解得:x=﹣,
∴点A的坐标为(﹣,0),
∴OA=.
∴S△AOB=OA?OB=.
故答案为:.
17.解:如图,过点D作DH⊥AC于H,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∵AB=2,BC=4,
∴AC===2,
∴OD=OC=,
∵S△ADC=×AD×DC=×AC×DH,
∴2×4=2×DH,
∴DH=,
∴OH===,
∴HC=﹣=,
∵CE⊥CA,DH⊥CA,
∴CE∥DH,
∴,
∴,
∴DE=.
18.解:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA===2,
∴OE=OA=2,
故答案为:2.
三.解答题(共8小题,满分78分)
19.解:(1)设一次函数解析式为y=kx+b(k≠0),
把x=﹣4,y=9;x=6,y=﹣1代入得:,
解得:,
则一次函数解析式为y=﹣x+5;
(2)y=﹣x+5,
∵k=﹣1<0,
∴y随x的增大而减小,
当y=﹣3时,﹣3=﹣x+5,即x=8,
当y=1时,1=﹣x+5,即x=4,
则当﹣3<y≤1时,自变量x的范围是4≤x<8.
20.解:(1)因为点P在x轴上,可得:5﹣a=0,
解得:a=5,
所以点P的坐标为(4,0);
故答案为:5;(4,0)
(2)因为点P是第一象限,可得:,
解得:1<a<5,
因为是整数,
所以a可以取2,3,4,
此时坐标分别为(1,3),(2,2),(3,1);
(3)若点P在第三象限,可得:,
此不等式组无解,
所以点P不可能在第三象限.
21.解:(1)14÷35%=40(人),a=40﹣14﹣12﹣8=6(人),
故答案为:6,40;
(2)补全频数分布直方图如下:
(3)“B组”所对应的圆心角的度数为:360°×=72°,
“C组”所对应的圆心角的度数为:360°×=108°,
(4)×100%=65%,
答:抽取学生成绩为“优秀”的人数占所抽取学生的百分比是65%.
22.证明:∵DE=BF,
∴DE+EF=BF+EF;
∴DF=BE;
在Rt△ADF和Rt△BCE中
,
∴Rt△ADF≌Rt△BCE,
∴AF=CE.
23.(1)证明∵E为AD的中点,
∴DE=AE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠EDC=∠EAF,
在△DEC和△AEF中,,
∴△DEC≌△AEF(AAS),
∴DC=FA,
∵AD=2AB,
∴AB=DE=EA=FA,
∴FB=AD;
(2)解:∵四边形ABCD是平行四边形,
∴DA∥CB,
∴∠CBF=∠DAF=70°,∠AEB=∠EBC,
又∵AE=AB,
∴∠AEB=∠ABE,
∴∠EBC=∠ABE=35°.
24.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,
∴∠BAD=∠ABC,
∴2∠BAD=180°,∴∠BAD=90°,
∴四边形ABCD是正方形;
(2)证明:∵四边形ABCD是正方形,
∴AC⊥BD,AC=BD,CO=AC,DO=BD,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,
∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,
∴∠ECO=∠EDH,
在△ECO和△FDO中,,
∴△ECO≌△FDO(ASA),
∴OE=OF.
25.解:(1)由图象可得小丽与小明出发30min相遇,
故答案为:30;
(2)①设小丽步行的速度为V1m/min,小明步行的速度为V2m/min,且V2>V1,
则,
解得:,
答:小丽步行的速度为80m/min,小明步行的速度为100m/min;
②解法一:设点C的坐标为(x,y),
则可得方程(100+80)(x﹣30)+80(67.5﹣x)=5400,
解得x=54,y=(100+80)(54﹣30)=4320m,
解法二:5400÷100=54,54×80=4320,
∴点C(54,4320),
点C表示:两人出发54min时,小明到达甲地,此时两人相距4320m.
26.解:(1)∵四边形ABCO为矩形,
∴CB=OA=10,AB=OC=6,
∵△CBM沿CM翻折后,点B落在x轴上,记作B′点,
∴CB′=CB=10,B′M=BM,
在Rt△OCB′中,OC=6,CB′=10,
∴OB′=8,
∴B′点的坐标为(8,0);
(2)设AM=t,则BM=B′M=6﹣t,
而AB′=OA﹣OB′=2,
在Rt△AB′M中,B′M2=B′A2+AM2,
即(6﹣t)2=22+t2,
解得t=,
∴M点的坐标为(10,),
设直线CM的解析式为y=kx+b,
把C(0,6)和M(10,)代入得,,解得,
∴直线CM的解析式为y=﹣x+6;
(3)存在,理由:
设点P的坐标为(x,0),
则△B′CP的面积=PB′×OC=|x﹣8|×6=13,
解得x=或,
故点P的坐标为(,0)或(,0).
同课章节目录
