福建省福州市平潭县高中2020-2021学年高一下学期6月月考数学试题 Word版含答案
文档属性
| 名称 | 福建省福州市平潭县高中2020-2021学年高一下学期6月月考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 851.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 22:52:46 | ||
图片预览




文档简介
平潭县高中2020-2021学年高一下学期6月月考1129030010718800
数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题1.设集合A={x|1≤x≤3},B={x|false<0},则A∩B=( )
A.{x|2<x≤3} B.{x|2≤x≤3} C.{x|1≤x<4} D.{x|1<x<4}
2.已知false,false,false,则false的最小值是( )A.3 B.4 C.5 D.6
3.下列函数中,既是偶函数,又在false上单调递增的是( )
A.false B.false C.false D.false
4.设false,false,false,则false,false,false的大小关系是( )
A.false B.false C.false D.false
5.欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它被誉为“数学中的天桥”.根据欧拉公式可知,e2i表示的复数在复平面中位于( )A第一象限 B第二象限 C第三象限 D第四象限
6.已知向量false,false,且false,则false( )A.falseB.false C.falseD.false
49530001206507.杭师大附中天文台是学校图书馆处的标志性建筑.小金同学为了测量天文台false的高度,选择附近学校宿舍楼三楼一阳台,高false为false,在它们之间的地面上的点M(B、M、D三点共线)处测得楼顶A、天文台顶C的仰角分别是false和false,在阳台A处测得天文台顶C的仰角为false,假设false和点M在同一平面内,则小金可测得学校天文台false的高度为( )A.falseB.falseC.falseD.false
8.下列结论中正确的是( )A.①②③ B.②④ C.③④ D.②③
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线中的一条相交,那么它也和另一条相交;④空间中有四条直线a,b,c,d,如果afalseb,cfalsed,且afalsed,那么bfalsec.
二、多选题
15684591122522771108915409.2020年7月16日,国家统计局发布2020年上半年中国经济数据.数据显示,上半年,全国居民人均消费支出9718元,较2019年上半年全国人均消费支出10330元,下降约5.9%(不考虑价格因素),图1、图2分别为2019年上半年与2020年上半年居民人均消费支出构成,则下列说法正确的是( )
A.2020年上半年较2019年上半年人均生活用品及服务消费支出减少了
B.2019年上半年人均衣着消费支出和人均居住消费支出的总和超过了人均食品烟酒消费支出
C.2020年上半年较2019年上半年人均居住消费支出减少了
D.2020年上半年较2019年上半年人均教育文化娱乐消费支出比重降幅最大
10.在false中,角A,B,C所对的边为a,b,c,有如下判断,其中正确的判断是( )
A.若false,则false为直角三角形 B.若false,则false
C.若false,则符合条件的是false有两个
D.若false,则false是钝角三角形
11.下列命题中是真命题的是( )
A.做7次抛掷一枚均匀硬币的试验,结果有4次出现正面,因此出现正面的概率是false
B.盒子中有大小均匀的3个黑球,2个白球,1个红球,则每种颜色被摸到的可能性相同
C.从-4,-3,-2,-1,0,1,2中任取一个数,取得小于0的概率大于取得不小于0的概率
D.分别从2名男生,2名女生中各选一名作为代表,则每名学生被选中的可能性相同
12.已知函数false,下面说法正确的有( )
A.false的图像关于原点对称 B.false的图像关于y轴对称
C.false的值域为false D.false,且false
三、填空题
13.在false中,false,false,false是false中点,则false__________.
14.如图,蹴鞠,又名“鞠球”“鞠圆”等,“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的踢足球活动.已知各顶点都在某“蹴”的表面上的正四棱柱的底面边长为false,高为false,球的体积为false,则这个正四棱柱的侧面积的最大值为_______.
15.某种心脏病手术,成功率为0.6,现准备进行3例此种手术,利用计算机取整数值随机数模拟,用0,1,2,3代表手术不成功,用4,5,6,7,8,9代表手术成功,产生20组随机数:966,907,191,924,270,832,912,468,578,582,134,370,113,573,998,397,027,488,703,725,则恰好成功1例的概率为________.
46958259969516.若函数false的部分图象如图所示,则false______,false______.
五、解答题
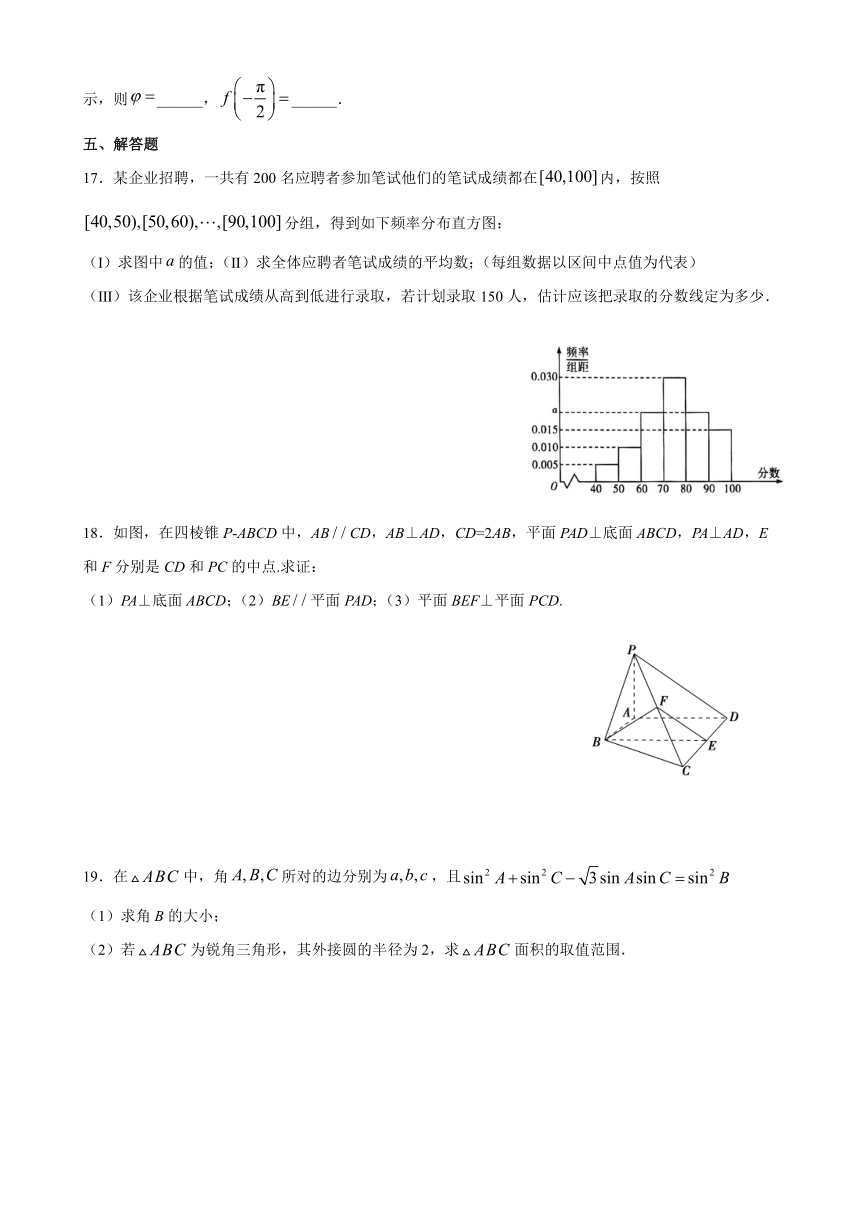
17.某企业招聘,一共有200名应聘者参加笔试他们的笔试成绩都在false内,按照false分组,得到如下频率分布直方图:
(Ⅰ)求图中false的值;(Ⅱ)求全体应聘者笔试成绩的平均数;(每组数据以区间中点值为代表)
3872230560070(Ⅲ)该企业根据笔试成绩从高到低进行录取,若计划录取150人,估计应该把录取的分数线定为多少.
18.如图,在四棱锥P?ABCD中,ABfalseCD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证:
(1)PA⊥底面ABCD;(2)BEfalse平面PAD;(3)平面BEF⊥平面PCD.
4467225232410
19.在false中,角false所对的边分别为false,且false
(1)求角B的大小;
(2)若false为锐角三角形,其外接圆的半径为2,求false面积的取值范围.
20.进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土地资源的消耗,具有社会?经济?生态等多方面的效益,是关乎生态文明建设全局的大事.为了普及垃圾分类知识,某学校举行了垃圾分类知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为false,乙同学答对每题的概率都为false,且在考试中每人各题答题结果互不影响.已知每题甲,乙同时答对的概率为false,恰有一人答对的概率为false.(1)求false和false的值;(2)试求两人共答对3道题的概率.
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品false(百台),其总成本为false(万元),其中固定成本为3万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入false,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:(1)写出利润函数false的解析式(利润=销售收入﹣总成本);(2)甲厂生产多少台新产品时,可使盈利最多?
22.已知直角梯形false中,false,如图①所示,将false沿false折起到false的位置,如图②所示.
(1)当平面false平面false时,求三棱锥false的体积;
3257550750570(2)在图②中,false为false的中点,若线段false,且false平面false,求线段false的长.
参考答案
1.A
【分析】
解得集合B,按照交集运算即可.
【详解】
解:∵A={x|1≤x≤3},B={x|2<x<4},
∴A∩B={x|2<x≤3}.
故选:A.
2.B
【分析】
根据基本不等式“1”的用法求解即可.
【详解】
因为false,false,false,
所以false,
当且仅当false时等号成立,
故选:B
【点睛】
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方
3.C
【分析】
对于A:利用函数奇偶性判断即可;
对于B:利用函数奇偶性判断即可;
对于C:先利用函数奇偶性判断偶函数,再判断单调性;
对于D:利用函数奇偶性判断即可.
【详解】
对于A:false的定义域为R,关于原点对称,因为false,所以false为奇函数,故A错误;
对于B:false的定义域为false,关于原点对称,因为false,所以false为奇函数,故B错误;
对于C:false的定义域为R,关于原点对称,因为false,所以false为偶函数;当false时,false为增函数,故C正确;
对于D:false的定义域为R,关于原点对称,但是false,而false,所以false,所以为非奇非偶函数,故D错误.
故选:C
【点睛】
(1)对函数奇偶性的证明只能用定义:false或false;
(2)函数奇偶性的应用:
①一般用false或false;
②有时为了计算简便,我们可以对x取特殊值: false或 false.
4.D
【分析】
根据指对数的性质,即可比较false,false,false的大小.
【详解】
由false,
∴false.
故选:D
5.B
【分析】
利用已知条件通过x=2代入,判断三角函数的符号,推出e3i表示的复数在复平面中所对应的点所在象限.
【详解】
eix=cosx+isinx(其中i为虚数单位,i2=﹣1),根据这个公式可知,e2i=cos2+isin2,
2弧度的角终边在第二象限.
故选:B
6.D
【分析】
本题首先可根据false求出false,然后根据false求出false,最后根据false即可得出结果.
【详解】
因为false,所以false,
因为false,false,
所以false,即false,false,
则false,
故选:D.
7.C
【分析】
利用正弦定理可得false,结合已知条件有false、false,即可求false的高度.
【详解】
由题意,false,false,即false,
∴△false中,false,则false,而false,
∵在△false中,false米.
故选:C
8.B
【分析】
根据空间中直线间的位置关系逐项进行判断即可.
【详解】
①错误,两条直线可以异面;
②正确,平行的传递性;
③错误,和另一条直线可以相交也可以异面;
④正确,平行的传递性.
故选:B.
9.ABD
【分析】
根据人均生活用品及服务消费支出占比,结合2020年、2019年上半年全国人均消费支出可判断选项A;根据2019年上半年人均衣着消费支出和人均居住消费支出的总和占比与人均食品烟酒消费支出占比可判断选项B;分别计算2020年上半年与2019年上半年人均居住消费支出,比较大小即可判断选项C;由图可知,人均教育文化娱乐消费支出比重降幅最大可判断选项D.
【详解】
解:对于选项A:2020年上半年和2019年上半年人均生活用品及服务消费支出占比均为6%,而2020年上半年人均消费支出比2019年上半年人均消费支出小,所以该项消费支出减少了,故选项A正确,
对于选项B:2019年上半年人均衣着消费支出和人均居住消费支出的总和占比30.2%,超过了人均食品烟酒消费支出所占比例28.6%,故选项B正确,
对于选项C:2019年上半年人均居住消费支出为10330×23.1%≈2386元,2020年上半年人均居住消费支出为9718×25.4%≈2468元,人均居住消费支出增加了,故选项C错误,
对于选项D:由图可知,人均教育文化娱乐消费支出比重降幅最大,为10%﹣6.8%=3.2%,故选项D正确,
故选:ABD.
【点睛】
本题主要考查数据统计题,主要根据扇形图中的信息给出相应的判断,主要考查学生的数据处理能力.
10.BD
【分析】
A.根据已知条件得到false或false,由此进行判断即可;
B.根据正弦定理得到边之间的关系,然后进行判断即可;
C.根据false之间的大小关系进行判断即可;
D.利用余弦定理计算出false的取值正负,从而进行判断.
【详解】
A.因为false,所以false或false,所以false或false,
所以false为等腰三角形或直角三角形,故错误;
B.因为false,所以false(false为false外接圆半径),
所以false,由“大边对大角”可知false,故正确;
C.因为false,所以没有符合条件的三角形,故错误;
D.因为false,所以false,所以false,
所以false为钝角,所以false是钝角三角形,故正确;
故选:BD.
【点睛】
结论点睛:在false中,角A,B,C所对的边为a,b,c,
结论(1):大边对大角,小边对小角;
结论(2):若false,可证明false为钝角三角形;若false且false为最大边,可证明false为锐角三角形(若未限定false为最大边,则无法说明).
11.CD
【分析】
根据题意求出各试验事件发生的概率,逐一判断即可得出选项.
【详解】
解析:A中,抛掷一枚硬币出现正面的概率是false,故错误;
B中,摸到黑球?白球?红球的可能性分别为false,false,false,故错误,
C中,取得小于0的概率为false,取得不小于0的概率为false,故正确;
D中,每名学生被选中的可能性都为false,故正确.
故选:CD.
12.ACD
【分析】
判断false的奇偶性即可判断选项AB,求false的值域可判断C,证明false的单调性可判断选项D,即可得正确选项.
【详解】
false的定义域为false关于原点对称,
false,所以false是奇函数,图象关于原点对称,
故选项A正确,选项B不正确;
false,因为false,所以false,所以false,
false,所以false,可得false的值域为false,故选项C正确;
设任意的false,
则false,
因为false,false,false,所以false,
即false,所以false,故选项D正确;
故选:ACD
【点睛】
利用定义证明函数单调性的方法
(1)取值:设false是该区间内的任意两个值,且false;
(2)作差变形:即作差,即作差false,并通过因式分解、配方、有理化等方法,向有利于判断符号的方向变形;
(3)定号:确定差false的符号;
(4)下结论:判断,根据定义作出结论.即取值---作差----变形----定号----下结论.
13.false 1
【分析】
根据图像波谷处函数值为false,所以false,由false,从而求出false,再根据特值false,false即可得解.
【详解】
由波谷处函数值为false,所以false,
false,所以false,
false,由false,
falsefalse,所以false,
false,
false
故答案为:false;1.
14.false
【分析】
由球的体积可确定其半径,根据正四棱柱外接球半径与底面外接圆半径和高之间关系可构造方程,求得false,根据侧面积公式可将侧面积false表示为关于false的函数,借助于基本不等式可求得结果.
【详解】
设球的半径为false,则false,解得:false;
false正四棱柱底面正方形外接圆半径false,又false,
false,解得:false,
false正四棱柱侧面积false,
false(当且仅当false,即false时取等号),false,
即正四棱柱侧面积的最大值为false.
故答案为:false.
【点睛】
思路点睛:本题考查立体几何中的最值问题的求解,求解此类问题的基本思路是将所求内容表示为关于某一变量的函数的形式,进而利用函数值域的求解方法或基本不等式求得最值.
15.0.4
【分析】
根据随机数,列举出设恰好成功1例的事件为A所包含的基本事件,再由古典概型的概率计算公式即可求解.
【详解】
解析:设恰好成功1例的事件为A,A所包含的基本事件为
191,270,832,912,134,370,027,703共8个.
则恰好成功1例的概率为P(A)=false=0.4.
故答案为:0.4
16.2
【分析】
分别以点A为坐标原点,AB为x轴,AC为y轴,建立平面直角坐标系,分别求出false和false的坐标,然后计算求值即可.
【详解】
分别以点A为坐标原点,AB为x轴,AC为y轴,建立平面直角坐标系,如下图:
所以false,设false,所以false,即false,
所以false,false,所以false.
故答案为:2.
【点睛】
方法点睛:解决向量数量积的问题,通常有两种思路,第一种思路是用定义,第二种是用坐标法,把向量用坐标去表示,使问题简单化.
17.(Ⅰ)false;(Ⅱ)74.5;(Ⅲ)65分.
【分析】
(1)根据频率和为1,即小矩形面积和为1,求false;(Ⅱ)利用每组数据中点值乘以本组的频率和,计算平均数;(Ⅲ)首先计算录取比例,根据录取比例求分数线.
【详解】
(Ⅰ)由题意false,
解得false.
(Ⅱ)这些应聘者笔试成绩的平均数为false.
(Ⅲ)根据题意,录取的比例为0.75,
设分数线定为false,根据频率分布直方图可知false,
且false,
解得false.
故估计应该把录取的分数线定为65分.
18.(1)证明见解析;(2)证明见解析;(3)证明见解析.
【分析】
(1)由面面垂直的性质定理可得;
(2)证明四边形ABED为平行四边形得BEfalseAD,然后由线面平行的判定定理可得;
(3)由 (1)的线面垂直得PA⊥CD,再底面四边形中垂直证明CD⊥平面PAD,得CD⊥PD,从而可证明CD⊥平面BEF,然后得证面面垂直.
【详解】
证明:(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为ABfalseCD,CD=2AB,E为CD的中点,
所以ABfalseDE,且AB=DE.
所以四边形ABED为平行四边形.所以BEfalseAD.
又因为BE?平面PAD,AD?平面PAD,
所以BEfalse平面PAD.
(3)因为AB⊥AD,而且四边形ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,false平面false,所以PA⊥CD.
又PA∩AD=A,所以CD⊥平面PAD,false平面false,所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PDfalseEF.所以CD⊥EF.
又因为CD⊥BE,EF∩BE=E,false平面false,所以CD⊥平面BEF.
因为CD?平面PCD,所以平面BEF⊥平面PCD.
【点睛】
关键点点睛:本题考查线面垂直的性质定理,线面平行和面面垂直的判定定理.解题关键是掌握定理的条件,解题过程中,定理的条件缺一不可,不写全条件,说理过程不完整.
19.(1)false;(2)false.
【分析】
(1)根据false,利用正弦定理得到false,再利用余弦定理求解;
(2)false为锐角三角形,由false,求得A的范围, 然后根据三角形的外接圆的半径为2,得到falsefalse,利用三角函数的性质求解.
【详解】
(1)因为false,
所以false,
所以false,
因为false,
所以false;
(2)因为false为锐角三角形,
所以false,则false,
即false,解得false,
又因为其外接圆的半径为2,
所以false,
所以false,
false,
false,
false,
false,
因为false,
所以false,
所以false,
所以false面积的取值范围是false.
【点睛】
方法得解:有关三角形面积问题的求解方法:(1)灵活运用正、余弦定理实现边角转化;(2)合理运用三角函数公式,如同角三角函数的基本关系、两角和与差的正弦、余弦公式、二倍角公式等.
20.(1)false,false;(2)false.
【分析】
(1)由互斥事件和对立事件的概率公式列方程组可解得false;
(2)分别求出两人答对1道的概率,答对两道题的概率,两人共答对3道题,则是一人答对2道题另一人答对1道题,由互斥事件和独立事件概率公式可得结论.
【详解】
解:(1)设false{甲同学答对第一题},false{乙同学答对第一题},则false,false.
设false{甲、乙二人均答对第一题},false{甲、乙二人中恰有一人答对第一题},
则false,false.
由于二人答题互不影响,且每人各题答题结果互不影响,所以false与false相互独立,false与false相互互斥,所以false,false
false.
由题意可得false
即false解得false或false
由于false,所以false,false.
(2)设false{甲同学答对了false道题},false{乙同学答对了false道题},false,1,2.
由题意得,false,false,
false,false.
设false{甲乙二人共答对3道题},则false.
由于false和false相互独立,false与false相互互斥,
所以false.
所以,甲乙二人共答对3道题的概率为false.
【点睛】
关键点点睛:本题考查互斥事件与独立事件的概率公式,解题关键是把所求概率事件用互斥事件表示,然后求概率,如设false{甲同学答对第一题},false{乙同学答对第一题},设false{甲、乙二人均答对第一题},false{甲、乙二人中恰有一人答对第一题},则false,false.同样两人共答对3题分拆成甲答对2题乙答对1题与甲答对1题乙答对2题两个互斥事件.
21.(1)false;(2)4百台.
【分析】
(1)由题意可得false,对false讨论false,false即可得到;
(2)分别讨论false,false的函数的单调性,即可得到最大值.
【详解】
(1)由题意得false,由false,
∴false.
(2)当false时,∵函数false递减,∴false(万元),
当false时,false,当false时,false有最大值为3.6(万元).
答:当工厂生产4百台时,可使赢利最大为3.6(万元).
【点睛】
关键点睛:本题主要考查函数的解析式的求法,考查分段函数的最值的求法,解题的关键是要认真审题,读懂题意,考查学生对知识的理解掌握水平和分析推理能力,属于基础题.
22.(1)false;(2)false
【分析】
(1)由面面垂直性质定理得false平面false,即为三棱锥false的高,再根据三棱锥体积公式求体积;
(2)取false的中点false,则根据三角形中位线性质得false,即得false,再根据线面平行性质定理得false.即得四边形false是平行四边形.可得false.
【详解】
(1)当平面false平面false时,因为false,且平面false平面false,false平面false,
所以false平面false,
因为false平面false,
所以false.
因为在直角梯形false中,false,false,false,false,false,
所以false,false.
所以false.
又因为false,所以false,所以false.
所以false.
所以三棱锥false的体积等于false.
(2)取false的中点false,连接false,false,如图所示.
又因为false为false的中点,
所以false,且false.
又因为false,
所以false.
所以false,false,false,false共面.
因为false平面false,false平面false,且平面false平面false,
所以false.
又因为false,
所以四边形false是平行四边形.
所以false.
【点睛】
将平面图形沿其中一条或几条线段折起,使其成为空间图形,把这类问题称为平面图形的翻折问题.平面图形经过翻折成为空间图形后,原有的性质有的发生了变化,有的没有发生变化,弄清它们是解决问题的关键.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.解决这类问题就是要据此研究翻折以后的空间图形中的线面关系和几何量的度量值,这是化解翻折问题难点的主要方法.立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.
数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题1.设集合A={x|1≤x≤3},B={x|false<0},则A∩B=( )
A.{x|2<x≤3} B.{x|2≤x≤3} C.{x|1≤x<4} D.{x|1<x<4}
2.已知false,false,false,则false的最小值是( )A.3 B.4 C.5 D.6
3.下列函数中,既是偶函数,又在false上单调递增的是( )
A.false B.false C.false D.false
4.设false,false,false,则false,false,false的大小关系是( )
A.false B.false C.false D.false
5.欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它被誉为“数学中的天桥”.根据欧拉公式可知,e2i表示的复数在复平面中位于( )A第一象限 B第二象限 C第三象限 D第四象限
6.已知向量false,false,且false,则false( )A.falseB.false C.falseD.false
49530001206507.杭师大附中天文台是学校图书馆处的标志性建筑.小金同学为了测量天文台false的高度,选择附近学校宿舍楼三楼一阳台,高false为false,在它们之间的地面上的点M(B、M、D三点共线)处测得楼顶A、天文台顶C的仰角分别是false和false,在阳台A处测得天文台顶C的仰角为false,假设false和点M在同一平面内,则小金可测得学校天文台false的高度为( )A.falseB.falseC.falseD.false
8.下列结论中正确的是( )A.①②③ B.②④ C.③④ D.②③
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线中的一条相交,那么它也和另一条相交;④空间中有四条直线a,b,c,d,如果afalseb,cfalsed,且afalsed,那么bfalsec.
二、多选题
15684591122522771108915409.2020年7月16日,国家统计局发布2020年上半年中国经济数据.数据显示,上半年,全国居民人均消费支出9718元,较2019年上半年全国人均消费支出10330元,下降约5.9%(不考虑价格因素),图1、图2分别为2019年上半年与2020年上半年居民人均消费支出构成,则下列说法正确的是( )
A.2020年上半年较2019年上半年人均生活用品及服务消费支出减少了
B.2019年上半年人均衣着消费支出和人均居住消费支出的总和超过了人均食品烟酒消费支出
C.2020年上半年较2019年上半年人均居住消费支出减少了
D.2020年上半年较2019年上半年人均教育文化娱乐消费支出比重降幅最大
10.在false中,角A,B,C所对的边为a,b,c,有如下判断,其中正确的判断是( )
A.若false,则false为直角三角形 B.若false,则false
C.若false,则符合条件的是false有两个
D.若false,则false是钝角三角形
11.下列命题中是真命题的是( )
A.做7次抛掷一枚均匀硬币的试验,结果有4次出现正面,因此出现正面的概率是false
B.盒子中有大小均匀的3个黑球,2个白球,1个红球,则每种颜色被摸到的可能性相同
C.从-4,-3,-2,-1,0,1,2中任取一个数,取得小于0的概率大于取得不小于0的概率
D.分别从2名男生,2名女生中各选一名作为代表,则每名学生被选中的可能性相同
12.已知函数false,下面说法正确的有( )
A.false的图像关于原点对称 B.false的图像关于y轴对称
C.false的值域为false D.false,且false
三、填空题
13.在false中,false,false,false是false中点,则false__________.
14.如图,蹴鞠,又名“鞠球”“鞠圆”等,“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的踢足球活动.已知各顶点都在某“蹴”的表面上的正四棱柱的底面边长为false,高为false,球的体积为false,则这个正四棱柱的侧面积的最大值为_______.
15.某种心脏病手术,成功率为0.6,现准备进行3例此种手术,利用计算机取整数值随机数模拟,用0,1,2,3代表手术不成功,用4,5,6,7,8,9代表手术成功,产生20组随机数:966,907,191,924,270,832,912,468,578,582,134,370,113,573,998,397,027,488,703,725,则恰好成功1例的概率为________.
46958259969516.若函数false的部分图象如图所示,则false______,false______.
五、解答题
17.某企业招聘,一共有200名应聘者参加笔试他们的笔试成绩都在false内,按照false分组,得到如下频率分布直方图:
(Ⅰ)求图中false的值;(Ⅱ)求全体应聘者笔试成绩的平均数;(每组数据以区间中点值为代表)
3872230560070(Ⅲ)该企业根据笔试成绩从高到低进行录取,若计划录取150人,估计应该把录取的分数线定为多少.
18.如图,在四棱锥P?ABCD中,ABfalseCD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.求证:
(1)PA⊥底面ABCD;(2)BEfalse平面PAD;(3)平面BEF⊥平面PCD.
4467225232410
19.在false中,角false所对的边分别为false,且false
(1)求角B的大小;
(2)若false为锐角三角形,其外接圆的半径为2,求false面积的取值范围.
20.进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土地资源的消耗,具有社会?经济?生态等多方面的效益,是关乎生态文明建设全局的大事.为了普及垃圾分类知识,某学校举行了垃圾分类知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为false,乙同学答对每题的概率都为false,且在考试中每人各题答题结果互不影响.已知每题甲,乙同时答对的概率为false,恰有一人答对的概率为false.(1)求false和false的值;(2)试求两人共答对3道题的概率.
甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品false(百台),其总成本为false(万元),其中固定成本为3万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入false,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:(1)写出利润函数false的解析式(利润=销售收入﹣总成本);(2)甲厂生产多少台新产品时,可使盈利最多?
22.已知直角梯形false中,false,如图①所示,将false沿false折起到false的位置,如图②所示.
(1)当平面false平面false时,求三棱锥false的体积;
3257550750570(2)在图②中,false为false的中点,若线段false,且false平面false,求线段false的长.
参考答案
1.A
【分析】
解得集合B,按照交集运算即可.
【详解】
解:∵A={x|1≤x≤3},B={x|2<x<4},
∴A∩B={x|2<x≤3}.
故选:A.
2.B
【分析】
根据基本不等式“1”的用法求解即可.
【详解】
因为false,false,false,
所以false,
当且仅当false时等号成立,
故选:B
【点睛】
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方
3.C
【分析】
对于A:利用函数奇偶性判断即可;
对于B:利用函数奇偶性判断即可;
对于C:先利用函数奇偶性判断偶函数,再判断单调性;
对于D:利用函数奇偶性判断即可.
【详解】
对于A:false的定义域为R,关于原点对称,因为false,所以false为奇函数,故A错误;
对于B:false的定义域为false,关于原点对称,因为false,所以false为奇函数,故B错误;
对于C:false的定义域为R,关于原点对称,因为false,所以false为偶函数;当false时,false为增函数,故C正确;
对于D:false的定义域为R,关于原点对称,但是false,而false,所以false,所以为非奇非偶函数,故D错误.
故选:C
【点睛】
(1)对函数奇偶性的证明只能用定义:false或false;
(2)函数奇偶性的应用:
①一般用false或false;
②有时为了计算简便,我们可以对x取特殊值: false或 false.
4.D
【分析】
根据指对数的性质,即可比较false,false,false的大小.
【详解】
由false,
∴false.
故选:D
5.B
【分析】
利用已知条件通过x=2代入,判断三角函数的符号,推出e3i表示的复数在复平面中所对应的点所在象限.
【详解】
eix=cosx+isinx(其中i为虚数单位,i2=﹣1),根据这个公式可知,e2i=cos2+isin2,
2弧度的角终边在第二象限.
故选:B
6.D
【分析】
本题首先可根据false求出false,然后根据false求出false,最后根据false即可得出结果.
【详解】
因为false,所以false,
因为false,false,
所以false,即false,false,
则false,
故选:D.
7.C
【分析】
利用正弦定理可得false,结合已知条件有false、false,即可求false的高度.
【详解】
由题意,false,false,即false,
∴△false中,false,则false,而false,
∵在△false中,false米.
故选:C
8.B
【分析】
根据空间中直线间的位置关系逐项进行判断即可.
【详解】
①错误,两条直线可以异面;
②正确,平行的传递性;
③错误,和另一条直线可以相交也可以异面;
④正确,平行的传递性.
故选:B.
9.ABD
【分析】
根据人均生活用品及服务消费支出占比,结合2020年、2019年上半年全国人均消费支出可判断选项A;根据2019年上半年人均衣着消费支出和人均居住消费支出的总和占比与人均食品烟酒消费支出占比可判断选项B;分别计算2020年上半年与2019年上半年人均居住消费支出,比较大小即可判断选项C;由图可知,人均教育文化娱乐消费支出比重降幅最大可判断选项D.
【详解】
解:对于选项A:2020年上半年和2019年上半年人均生活用品及服务消费支出占比均为6%,而2020年上半年人均消费支出比2019年上半年人均消费支出小,所以该项消费支出减少了,故选项A正确,
对于选项B:2019年上半年人均衣着消费支出和人均居住消费支出的总和占比30.2%,超过了人均食品烟酒消费支出所占比例28.6%,故选项B正确,
对于选项C:2019年上半年人均居住消费支出为10330×23.1%≈2386元,2020年上半年人均居住消费支出为9718×25.4%≈2468元,人均居住消费支出增加了,故选项C错误,
对于选项D:由图可知,人均教育文化娱乐消费支出比重降幅最大,为10%﹣6.8%=3.2%,故选项D正确,
故选:ABD.
【点睛】
本题主要考查数据统计题,主要根据扇形图中的信息给出相应的判断,主要考查学生的数据处理能力.
10.BD
【分析】
A.根据已知条件得到false或false,由此进行判断即可;
B.根据正弦定理得到边之间的关系,然后进行判断即可;
C.根据false之间的大小关系进行判断即可;
D.利用余弦定理计算出false的取值正负,从而进行判断.
【详解】
A.因为false,所以false或false,所以false或false,
所以false为等腰三角形或直角三角形,故错误;
B.因为false,所以false(false为false外接圆半径),
所以false,由“大边对大角”可知false,故正确;
C.因为false,所以没有符合条件的三角形,故错误;
D.因为false,所以false,所以false,
所以false为钝角,所以false是钝角三角形,故正确;
故选:BD.
【点睛】
结论点睛:在false中,角A,B,C所对的边为a,b,c,
结论(1):大边对大角,小边对小角;
结论(2):若false,可证明false为钝角三角形;若false且false为最大边,可证明false为锐角三角形(若未限定false为最大边,则无法说明).
11.CD
【分析】
根据题意求出各试验事件发生的概率,逐一判断即可得出选项.
【详解】
解析:A中,抛掷一枚硬币出现正面的概率是false,故错误;
B中,摸到黑球?白球?红球的可能性分别为false,false,false,故错误,
C中,取得小于0的概率为false,取得不小于0的概率为false,故正确;
D中,每名学生被选中的可能性都为false,故正确.
故选:CD.
12.ACD
【分析】
判断false的奇偶性即可判断选项AB,求false的值域可判断C,证明false的单调性可判断选项D,即可得正确选项.
【详解】
false的定义域为false关于原点对称,
false,所以false是奇函数,图象关于原点对称,
故选项A正确,选项B不正确;
false,因为false,所以false,所以false,
false,所以false,可得false的值域为false,故选项C正确;
设任意的false,
则false,
因为false,false,false,所以false,
即false,所以false,故选项D正确;
故选:ACD
【点睛】
利用定义证明函数单调性的方法
(1)取值:设false是该区间内的任意两个值,且false;
(2)作差变形:即作差,即作差false,并通过因式分解、配方、有理化等方法,向有利于判断符号的方向变形;
(3)定号:确定差false的符号;
(4)下结论:判断,根据定义作出结论.即取值---作差----变形----定号----下结论.
13.false 1
【分析】
根据图像波谷处函数值为false,所以false,由false,从而求出false,再根据特值false,false即可得解.
【详解】
由波谷处函数值为false,所以false,
false,所以false,
false,由false,
falsefalse,所以false,
false,
false
故答案为:false;1.
14.false
【分析】
由球的体积可确定其半径,根据正四棱柱外接球半径与底面外接圆半径和高之间关系可构造方程,求得false,根据侧面积公式可将侧面积false表示为关于false的函数,借助于基本不等式可求得结果.
【详解】
设球的半径为false,则false,解得:false;
false正四棱柱底面正方形外接圆半径false,又false,
false,解得:false,
false正四棱柱侧面积false,
false(当且仅当false,即false时取等号),false,
即正四棱柱侧面积的最大值为false.
故答案为:false.
【点睛】
思路点睛:本题考查立体几何中的最值问题的求解,求解此类问题的基本思路是将所求内容表示为关于某一变量的函数的形式,进而利用函数值域的求解方法或基本不等式求得最值.
15.0.4
【分析】
根据随机数,列举出设恰好成功1例的事件为A所包含的基本事件,再由古典概型的概率计算公式即可求解.
【详解】
解析:设恰好成功1例的事件为A,A所包含的基本事件为
191,270,832,912,134,370,027,703共8个.
则恰好成功1例的概率为P(A)=false=0.4.
故答案为:0.4
16.2
【分析】
分别以点A为坐标原点,AB为x轴,AC为y轴,建立平面直角坐标系,分别求出false和false的坐标,然后计算求值即可.
【详解】
分别以点A为坐标原点,AB为x轴,AC为y轴,建立平面直角坐标系,如下图:
所以false,设false,所以false,即false,
所以false,false,所以false.
故答案为:2.
【点睛】
方法点睛:解决向量数量积的问题,通常有两种思路,第一种思路是用定义,第二种是用坐标法,把向量用坐标去表示,使问题简单化.
17.(Ⅰ)false;(Ⅱ)74.5;(Ⅲ)65分.
【分析】
(1)根据频率和为1,即小矩形面积和为1,求false;(Ⅱ)利用每组数据中点值乘以本组的频率和,计算平均数;(Ⅲ)首先计算录取比例,根据录取比例求分数线.
【详解】
(Ⅰ)由题意false,
解得false.
(Ⅱ)这些应聘者笔试成绩的平均数为false.
(Ⅲ)根据题意,录取的比例为0.75,
设分数线定为false,根据频率分布直方图可知false,
且false,
解得false.
故估计应该把录取的分数线定为65分.
18.(1)证明见解析;(2)证明见解析;(3)证明见解析.
【分析】
(1)由面面垂直的性质定理可得;
(2)证明四边形ABED为平行四边形得BEfalseAD,然后由线面平行的判定定理可得;
(3)由 (1)的线面垂直得PA⊥CD,再底面四边形中垂直证明CD⊥平面PAD,得CD⊥PD,从而可证明CD⊥平面BEF,然后得证面面垂直.
【详解】
证明:(1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,
所以PA⊥底面ABCD.
(2)因为ABfalseCD,CD=2AB,E为CD的中点,
所以ABfalseDE,且AB=DE.
所以四边形ABED为平行四边形.所以BEfalseAD.
又因为BE?平面PAD,AD?平面PAD,
所以BEfalse平面PAD.
(3)因为AB⊥AD,而且四边形ABED为平行四边形,
所以BE⊥CD,AD⊥CD.
由(1)知PA⊥底面ABCD,false平面false,所以PA⊥CD.
又PA∩AD=A,所以CD⊥平面PAD,false平面false,所以CD⊥PD.
因为E和F分别是CD和PC的中点,
所以PDfalseEF.所以CD⊥EF.
又因为CD⊥BE,EF∩BE=E,false平面false,所以CD⊥平面BEF.
因为CD?平面PCD,所以平面BEF⊥平面PCD.
【点睛】
关键点点睛:本题考查线面垂直的性质定理,线面平行和面面垂直的判定定理.解题关键是掌握定理的条件,解题过程中,定理的条件缺一不可,不写全条件,说理过程不完整.
19.(1)false;(2)false.
【分析】
(1)根据false,利用正弦定理得到false,再利用余弦定理求解;
(2)false为锐角三角形,由false,求得A的范围, 然后根据三角形的外接圆的半径为2,得到falsefalse,利用三角函数的性质求解.
【详解】
(1)因为false,
所以false,
所以false,
因为false,
所以false;
(2)因为false为锐角三角形,
所以false,则false,
即false,解得false,
又因为其外接圆的半径为2,
所以false,
所以false,
false,
false,
false,
false,
因为false,
所以false,
所以false,
所以false面积的取值范围是false.
【点睛】
方法得解:有关三角形面积问题的求解方法:(1)灵活运用正、余弦定理实现边角转化;(2)合理运用三角函数公式,如同角三角函数的基本关系、两角和与差的正弦、余弦公式、二倍角公式等.
20.(1)false,false;(2)false.
【分析】
(1)由互斥事件和对立事件的概率公式列方程组可解得false;
(2)分别求出两人答对1道的概率,答对两道题的概率,两人共答对3道题,则是一人答对2道题另一人答对1道题,由互斥事件和独立事件概率公式可得结论.
【详解】
解:(1)设false{甲同学答对第一题},false{乙同学答对第一题},则false,false.
设false{甲、乙二人均答对第一题},false{甲、乙二人中恰有一人答对第一题},
则false,false.
由于二人答题互不影响,且每人各题答题结果互不影响,所以false与false相互独立,false与false相互互斥,所以false,false
false.
由题意可得false
即false解得false或false
由于false,所以false,false.
(2)设false{甲同学答对了false道题},false{乙同学答对了false道题},false,1,2.
由题意得,false,false,
false,false.
设false{甲乙二人共答对3道题},则false.
由于false和false相互独立,false与false相互互斥,
所以false.
所以,甲乙二人共答对3道题的概率为false.
【点睛】
关键点点睛:本题考查互斥事件与独立事件的概率公式,解题关键是把所求概率事件用互斥事件表示,然后求概率,如设false{甲同学答对第一题},false{乙同学答对第一题},设false{甲、乙二人均答对第一题},false{甲、乙二人中恰有一人答对第一题},则false,false.同样两人共答对3题分拆成甲答对2题乙答对1题与甲答对1题乙答对2题两个互斥事件.
21.(1)false;(2)4百台.
【分析】
(1)由题意可得false,对false讨论false,false即可得到;
(2)分别讨论false,false的函数的单调性,即可得到最大值.
【详解】
(1)由题意得false,由false,
∴false.
(2)当false时,∵函数false递减,∴false(万元),
当false时,false,当false时,false有最大值为3.6(万元).
答:当工厂生产4百台时,可使赢利最大为3.6(万元).
【点睛】
关键点睛:本题主要考查函数的解析式的求法,考查分段函数的最值的求法,解题的关键是要认真审题,读懂题意,考查学生对知识的理解掌握水平和分析推理能力,属于基础题.
22.(1)false;(2)false
【分析】
(1)由面面垂直性质定理得false平面false,即为三棱锥false的高,再根据三棱锥体积公式求体积;
(2)取false的中点false,则根据三角形中位线性质得false,即得false,再根据线面平行性质定理得false.即得四边形false是平行四边形.可得false.
【详解】
(1)当平面false平面false时,因为false,且平面false平面false,false平面false,
所以false平面false,
因为false平面false,
所以false.
因为在直角梯形false中,false,false,false,false,false,
所以false,false.
所以false.
又因为false,所以false,所以false.
所以false.
所以三棱锥false的体积等于false.
(2)取false的中点false,连接false,false,如图所示.
又因为false为false的中点,
所以false,且false.
又因为false,
所以false.
所以false,false,false,false共面.
因为false平面false,false平面false,且平面false平面false,
所以false.
又因为false,
所以四边形false是平行四边形.
所以false.
【点睛】
将平面图形沿其中一条或几条线段折起,使其成为空间图形,把这类问题称为平面图形的翻折问题.平面图形经过翻折成为空间图形后,原有的性质有的发生了变化,有的没有发生变化,弄清它们是解决问题的关键.一般地,翻折后还在同一个平面上的性质不发生变化,不在同一个平面上的性质发生变化.解决这类问题就是要据此研究翻折以后的空间图形中的线面关系和几何量的度量值,这是化解翻折问题难点的主要方法.立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.
同课章节目录
