北京市海淀区实高2020-2021学年高二下学期6月月考数学试题 Word版含答案
文档属性
| 名称 | 北京市海淀区实高2020-2021学年高二下学期6月月考数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 00:00:00 | ||
图片预览




文档简介
北京市海淀实验中学2020-2021学年高二(下)6月月考数学试题
数 学
班级:__________ 姓名:__________ 学号:__________
一、选择题(共10小题;共50分)
1. 已知 , 独立,且 ,则
A. B. C. D.
2. 如果,从甲地到乙地有 条路,从乙地到丁地有 条路;从甲地到丙地有 条路,从丙地到丁地有 条路.从甲地到丁地的不同路线共有
A. 条 B. 条 C. 条 D. 条
3. 设数列 是等差数列,,,则这个数列的前 项和等于
A. B. C. D.21
4. 已知离散型随机变量 的分布列如下,则
A. B. C. D.
5. 已知数列 的前 项和 ,则
A. B. C. D.
6. 的展开式中常数项是
A. B. 32 C. D. 16
7. 在等比数列 中,,,则 的前 项和为
A. B. C. D.
8. 设 ,若 在 处的导数 ,则 的值为
A. B. C. D.
9. 某次联欢会要安排 个歌舞类节目、 个小品类节目和 个相声类节目的演出顺序,则同类节目不相邻的排法种数
A. B. 144 C. 120 D.
10. 已知函数 ,若 有四个不同的零点,则 的取值范围为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 设常数 ,如果 的二项展开式中 项的系数为 ,那么 ?.
12. 已知 的分布列如表,设 ,则 的数学期望 的值是 ?.
13. 从 ,,, 中,甲,乙两人依次任取一数(不放回),在已知甲取到的数是 的倍数的条件下,甲取的数大于乙取的数的概率是 ?.
14. 投篮测试中,每人投 次,至少投中 次才能通过测试.已知某同学每次投篮投中的概率为 ,且每次投篮是否投中相互独立,则该同学通过测试的概率为 ?.
15. 设集合 ,那么集合 中满足条件“”的元素个数为 ?.
三、解答题(共6小题;共78分)
16. 已知 是公差为 的等差数列,其前 项和为 ,且 , ?.若存在正整数 ,使得 有最小值.
从① ,② ,③ 这三个条件中选择符合题意的一个条件,补充在上面问题中并作答.
(1)求 的通项公式;
(2)求 的最小值.
17. 甲、乙等五名奥运志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加 岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量 为这五名志愿者中参加 岗位服务的人数,求 的分布列.
18. 已知函数 ,.
(1)若曲线 在点 处的切线平行于直线 ,求该切线方程.
(2)若 ,求证:当 时,.
(3)若 恰有两个零点,求 的值.
19. 已知数列 是由正数组成的等比数列,,且 ,, 成等差数列.
(1)求数列 的通项公式.
(2)数列 的前 项和为 ,若 ,求实数 的值.
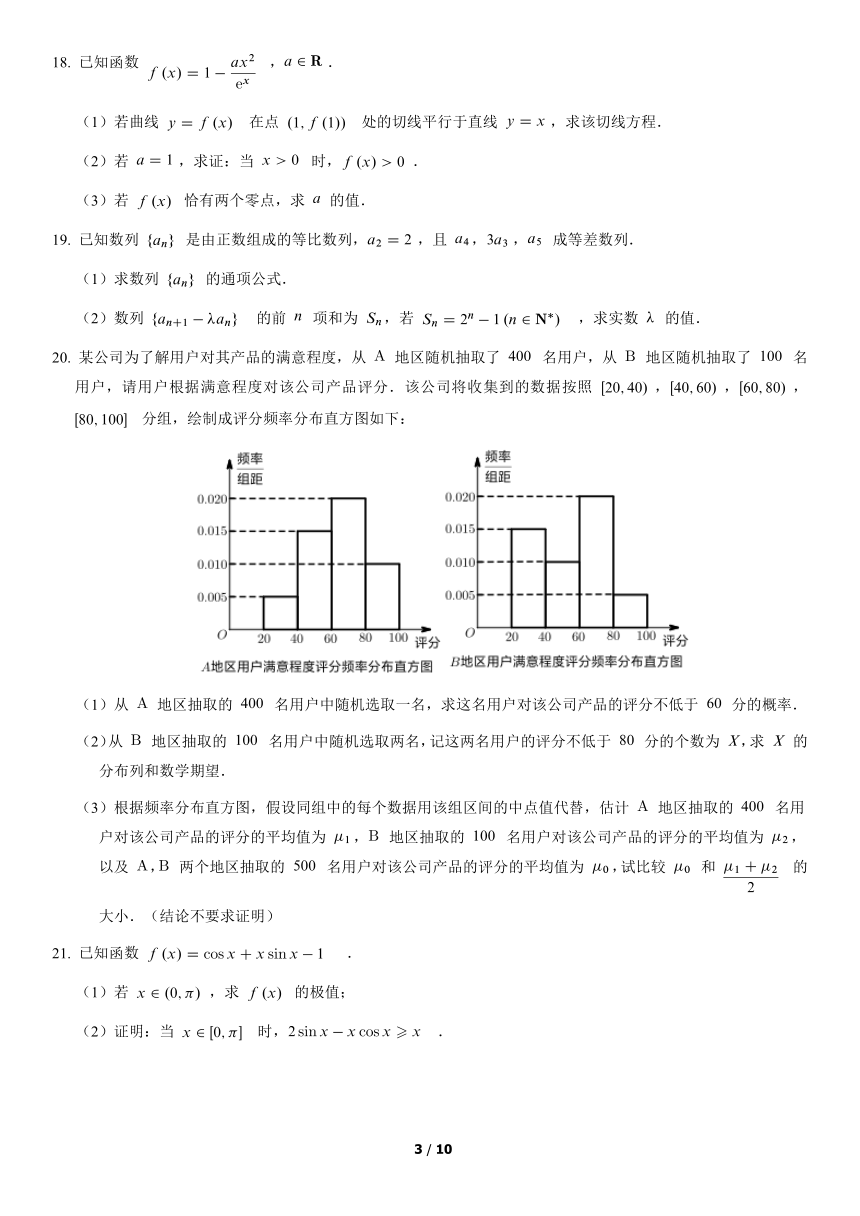
20. 某公司为了解用户对其产品的满意程度,从 地区随机抽取了 名用户,从 地区随机抽取了 名用户,请用户根据满意程度对该公司产品评分.该公司将收集到的数据按照 ,,, 分组,绘制成评分频率分布直方图如下:
(1)从 地区抽取的 名用户中随机选取一名,求这名用户对该公司产品的评分不低于 分的概率.
(2)从 地区抽取的 名用户中随机选取两名,记这两名用户的评分不低于 分的个数为 ,求 的分布列和数学期望.
(3)根据频率分布直方图,假设同组中的每个数据用该组区间的中点值代替,估计 地区抽取的 名用户对该公司产品的评分的平均值为 , 地区抽取的 名用户对该公司产品的评分的平均值为 ,以及 , 两个地区抽取的 名用户对该公司产品的评分的平均值为 ,试比较 和 的大小.(结论不要求证明)
21. 已知函数 .
(1)若 ,求 的极值;
(2)证明:当 时,.
北京市海淀实验中学2020-2021学年高二(下)6月月考数学试题
参考答案
第一部分
1. B 【解析】因为 , 独立,
所以 .
2. C 【解析】若经乙地,则有 条,
若经甲地,则有 条,
故共有 条.
3. D
4. B 【解析】由已知得 .
所以 .
5. B
6. D 【解析】二项式 的通项公式为 ,
令 ,解得 ,
则 的展开式中常数项是 .
7. A
8. B 【解析】由 ,得 .
由 ,解得:.
9. C 【解析】将所有的安排方法分成两类,
第一类:歌舞类节目中间不穿插相声节目,有 种;
第二类:歌舞类节目中间穿插相声节目,有 种.
根据分类加法计数原理,共有 种不同的排法.
10. A
【解析】作出 的图象如下:
若 有四个不同的零点,
则 有四个根,
即 与 有四个交点,
直线 过原点,
当 时, 与 有两个交点,
当 时,直线 与 相切时,
不妨设切点为 ,
则
,
所以
由①②③得 ,,
所以切线的斜率为 ,
若 与 有四个交点,则 ,
综上, 的取值范围为 .
第二部分
11.
【解析】 的二项展开式的通项公式:,
令 ,解得 .
所以 ,
解得 .
12.
【解析】由已知得 ,所以 ,
所以 ,
因为 ,所以 .
13.
【解析】,,.
14.
【解析】该同学通过测试的概率 .
15.
【解析】分三种情况讨论:
(),则上述五个数中有一个为 或 ,
其余 个数为零,此时有 个元素;
(),则上述五个数中有两个数为 或 ,
其余三个数为零,此时 中有 个元素;
(),则上述五个数中有三个数为 或 ,
其余两个数为零,此时 中有 个元素.
综上一共有 个元素.
16. (1) (不可以选择③作为补充条件)
选择①作为补充条件.解答如下:
因为 ,,所以 .
所以 .
选择②作为补充条件.解答如下:
因为 ,,
所以 .
(2) 选择①作为补充条件.解答如下:
由(Ⅰ)可知 .
所以 .
因为 ,所以当 或 时, 取得最小值,最小值为 .
故存在正整数 或 ,使得 有最小值,最小值为 .
选择②作为补充条件.解答如下:
由(Ⅰ)可知 .
所以 .
所以当 时, 取得最小值,最小值为 .
故存在正整数 ,使得 有最小值,最小值为 .
17. (1) 记甲、乙两人同时参加 岗位服务为事件 ,那么
即甲、乙两人同时参加 岗位服务的概率是 .
(2) 记甲、乙两人同时参加同一岗位服务为事件 ,那么
所以,甲、乙两人不在同一岗位服务的概率是
(3) 随机变量 可能取的值为 .
事件" "是指有两人同时参加 岗位服务,则
所以
的分布列是:
18. (1) 的导函数为 ,
因为 在 处的切线与 平行,
所以
所以 ,
所以 ,
所以切线方程为 .
(2) 时,,,
所以 时, 即 单调递减;
时, 即 单调递增;
所以 ,
所以 时,.
(3) 由()知 ,
显然 时, 恒成立,故 ,
① 时, 时,,即 单调递增;
时,,即 单调递减;
时,,即 单调递增;
若 恰有两个零点,则 或
因为 ,
所以 ,即 ;
② 时, 恒成立,故 恒成立,
所以 恒成立,
所以 无零点.
综上所述,.
19. (1) 设数列 的公比为 .
因为 ,, 成等差数列,
所以 ,
所以 .
因为 ,
所以 .
所以 .
(2) 由()知,,,
所以 .
所以 ,
所以 .
20. (1) 由频率分布直方图可得不低于 分的概率为:.
(2) 由题可知 的可能取值为 ,,.
;
;
.
所以 的分布列如下表:
所以 的数学期望 .
(3) .
21. (1) 因为 ,
所以 ,
当 时,;
当 时,,
当 发生变化时,, 的变化情况如下表:
因此,当 时, 有极大值,并且极大值为 ,没有极小值.
??????(2) 令 ,
则 ,
由()知 在 上单调递增,在 上单调递减.
又 ,,,
所以 在 上存在唯一零点,设为 ,则 ,
当 时,;当 时,,
所以 在区间 上单调递增,在区间 上单调递减,
又 ,,
所以当 时,,
故 .
数 学
班级:__________ 姓名:__________ 学号:__________
一、选择题(共10小题;共50分)
1. 已知 , 独立,且 ,则
A. B. C. D.
2. 如果,从甲地到乙地有 条路,从乙地到丁地有 条路;从甲地到丙地有 条路,从丙地到丁地有 条路.从甲地到丁地的不同路线共有
A. 条 B. 条 C. 条 D. 条
3. 设数列 是等差数列,,,则这个数列的前 项和等于
A. B. C. D.21
4. 已知离散型随机变量 的分布列如下,则
A. B. C. D.
5. 已知数列 的前 项和 ,则
A. B. C. D.
6. 的展开式中常数项是
A. B. 32 C. D. 16
7. 在等比数列 中,,,则 的前 项和为
A. B. C. D.
8. 设 ,若 在 处的导数 ,则 的值为
A. B. C. D.
9. 某次联欢会要安排 个歌舞类节目、 个小品类节目和 个相声类节目的演出顺序,则同类节目不相邻的排法种数
A. B. 144 C. 120 D.
10. 已知函数 ,若 有四个不同的零点,则 的取值范围为
A. B. C. D.
二、填空题(共5小题;共25分)
11. 设常数 ,如果 的二项展开式中 项的系数为 ,那么 ?.
12. 已知 的分布列如表,设 ,则 的数学期望 的值是 ?.
13. 从 ,,, 中,甲,乙两人依次任取一数(不放回),在已知甲取到的数是 的倍数的条件下,甲取的数大于乙取的数的概率是 ?.
14. 投篮测试中,每人投 次,至少投中 次才能通过测试.已知某同学每次投篮投中的概率为 ,且每次投篮是否投中相互独立,则该同学通过测试的概率为 ?.
15. 设集合 ,那么集合 中满足条件“”的元素个数为 ?.
三、解答题(共6小题;共78分)
16. 已知 是公差为 的等差数列,其前 项和为 ,且 , ?.若存在正整数 ,使得 有最小值.
从① ,② ,③ 这三个条件中选择符合题意的一个条件,补充在上面问题中并作答.
(1)求 的通项公式;
(2)求 的最小值.
17. 甲、乙等五名奥运志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加 岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量 为这五名志愿者中参加 岗位服务的人数,求 的分布列.
18. 已知函数 ,.
(1)若曲线 在点 处的切线平行于直线 ,求该切线方程.
(2)若 ,求证:当 时,.
(3)若 恰有两个零点,求 的值.
19. 已知数列 是由正数组成的等比数列,,且 ,, 成等差数列.
(1)求数列 的通项公式.
(2)数列 的前 项和为 ,若 ,求实数 的值.
20. 某公司为了解用户对其产品的满意程度,从 地区随机抽取了 名用户,从 地区随机抽取了 名用户,请用户根据满意程度对该公司产品评分.该公司将收集到的数据按照 ,,, 分组,绘制成评分频率分布直方图如下:
(1)从 地区抽取的 名用户中随机选取一名,求这名用户对该公司产品的评分不低于 分的概率.
(2)从 地区抽取的 名用户中随机选取两名,记这两名用户的评分不低于 分的个数为 ,求 的分布列和数学期望.
(3)根据频率分布直方图,假设同组中的每个数据用该组区间的中点值代替,估计 地区抽取的 名用户对该公司产品的评分的平均值为 , 地区抽取的 名用户对该公司产品的评分的平均值为 ,以及 , 两个地区抽取的 名用户对该公司产品的评分的平均值为 ,试比较 和 的大小.(结论不要求证明)
21. 已知函数 .
(1)若 ,求 的极值;
(2)证明:当 时,.
北京市海淀实验中学2020-2021学年高二(下)6月月考数学试题
参考答案
第一部分
1. B 【解析】因为 , 独立,
所以 .
2. C 【解析】若经乙地,则有 条,
若经甲地,则有 条,
故共有 条.
3. D
4. B 【解析】由已知得 .
所以 .
5. B
6. D 【解析】二项式 的通项公式为 ,
令 ,解得 ,
则 的展开式中常数项是 .
7. A
8. B 【解析】由 ,得 .
由 ,解得:.
9. C 【解析】将所有的安排方法分成两类,
第一类:歌舞类节目中间不穿插相声节目,有 种;
第二类:歌舞类节目中间穿插相声节目,有 种.
根据分类加法计数原理,共有 种不同的排法.
10. A
【解析】作出 的图象如下:
若 有四个不同的零点,
则 有四个根,
即 与 有四个交点,
直线 过原点,
当 时, 与 有两个交点,
当 时,直线 与 相切时,
不妨设切点为 ,
则
,
所以
由①②③得 ,,
所以切线的斜率为 ,
若 与 有四个交点,则 ,
综上, 的取值范围为 .
第二部分
11.
【解析】 的二项展开式的通项公式:,
令 ,解得 .
所以 ,
解得 .
12.
【解析】由已知得 ,所以 ,
所以 ,
因为 ,所以 .
13.
【解析】,,.
14.
【解析】该同学通过测试的概率 .
15.
【解析】分三种情况讨论:
(),则上述五个数中有一个为 或 ,
其余 个数为零,此时有 个元素;
(),则上述五个数中有两个数为 或 ,
其余三个数为零,此时 中有 个元素;
(),则上述五个数中有三个数为 或 ,
其余两个数为零,此时 中有 个元素.
综上一共有 个元素.
16. (1) (不可以选择③作为补充条件)
选择①作为补充条件.解答如下:
因为 ,,所以 .
所以 .
选择②作为补充条件.解答如下:
因为 ,,
所以 .
(2) 选择①作为补充条件.解答如下:
由(Ⅰ)可知 .
所以 .
因为 ,所以当 或 时, 取得最小值,最小值为 .
故存在正整数 或 ,使得 有最小值,最小值为 .
选择②作为补充条件.解答如下:
由(Ⅰ)可知 .
所以 .
所以当 时, 取得最小值,最小值为 .
故存在正整数 ,使得 有最小值,最小值为 .
17. (1) 记甲、乙两人同时参加 岗位服务为事件 ,那么
即甲、乙两人同时参加 岗位服务的概率是 .
(2) 记甲、乙两人同时参加同一岗位服务为事件 ,那么
所以,甲、乙两人不在同一岗位服务的概率是
(3) 随机变量 可能取的值为 .
事件" "是指有两人同时参加 岗位服务,则
所以
的分布列是:
18. (1) 的导函数为 ,
因为 在 处的切线与 平行,
所以
所以 ,
所以 ,
所以切线方程为 .
(2) 时,,,
所以 时, 即 单调递减;
时, 即 单调递增;
所以 ,
所以 时,.
(3) 由()知 ,
显然 时, 恒成立,故 ,
① 时, 时,,即 单调递增;
时,,即 单调递减;
时,,即 单调递增;
若 恰有两个零点,则 或
因为 ,
所以 ,即 ;
② 时, 恒成立,故 恒成立,
所以 恒成立,
所以 无零点.
综上所述,.
19. (1) 设数列 的公比为 .
因为 ,, 成等差数列,
所以 ,
所以 .
因为 ,
所以 .
所以 .
(2) 由()知,,,
所以 .
所以 ,
所以 .
20. (1) 由频率分布直方图可得不低于 分的概率为:.
(2) 由题可知 的可能取值为 ,,.
;
;
.
所以 的分布列如下表:
所以 的数学期望 .
(3) .
21. (1) 因为 ,
所以 ,
当 时,;
当 时,,
当 发生变化时,, 的变化情况如下表:
因此,当 时, 有极大值,并且极大值为 ,没有极小值.
??????(2) 令 ,
则 ,
由()知 在 上单调递增,在 上单调递减.
又 ,,,
所以 在 上存在唯一零点,设为 ,则 ,
当 时,;当 时,,
所以 在区间 上单调递增,在区间 上单调递减,
又 ,,
所以当 时,,
故 .
同课章节目录
