江西省永丰县高中2020-2021学年高一下学期6月月考数学试题 Word版含答案
文档属性
| 名称 | 江西省永丰县高中2020-2021学年高一下学期6月月考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 845.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 22:56:11 | ||
图片预览

文档简介
永丰中学2020-2021学年高一下学期6月月考1075690011696700
数学试卷(必修3)
★查漏补缺,积极备考,再创辉煌!
一、选择题
1.某中学进行了该学年度期末统一考试,该校为了了解高一年级1000名学生的考试成绩,从中随机抽取了100名学生的成绩,就这个问题来说,下面说法正确的是( )
A.1000名学生是总体 B.每个学生是个体
C.1000名学生的成绩是一个个体 D.样本的容量是100
2.人民礼堂有50排座位,每排有60个座位号,一次报告会坐满了听众,会后留下座位号为18的所有听众50人进行座谈,这是运用了( )
A.抽签法 B.随机数法 C.系统抽样 D.放回抽样
3.给出下列4个说法:①概率为0的事件是不可能事件;②若某种彩票的中奖概率为false,则购买1000张彩票至少有一张中奖;③在一次随机试验中,任何两个基本事件都是对立事件;④两个互斥事件的概率之和等于1.其中正确说法的个数是( )
A.0 B.1 C.2 D.3
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为x,y,105,109,110.已知她的五次数学成绩数据的平均数为108分,方差为35.2,则|x-y|的值为( )
A.15 B.16 C.17 D.18
5.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A.false B.false C.false D.false
6.200辆汽车通过某一段公路时时速的频率分布直方图如图,则时速的众数、中位数的估计值为( )
A.62 km/h,62.5 km/h B.65 km/h,62 km/h C.65 km/h,62.5 km/h D.62.5 km/h,62.5 km/h
7.连抛两次骰子,以先后得到的点数m,n为P(m,n))坐标,那么点P在圆false内部的概率是( )
A.false B.false C.false D.false
8.某赛季甲?乙两名篮球运动员13场比赛得分情况用茎叶图表示如下:根据茎叶图,对这两名运动员的成绩进行比较,下列结论不正确的是( )
A.甲运动员得分的极差大于乙运动员的极差 B.甲运动员得分的中位数大于乙运动员的中位数
C.甲运动员得分的平均值大于乙运动员的平均值 D.甲运动员的成绩比乙运动员的成绩稳定
9.某企业有职工80000人,其职工年龄情况和绿色出行情况如下图,则正确的是( )
753745936625中年职工
中年职工
A.该企业老年职工绿色出行的人数最多 B.该企业青年职工绿色出行的人数最多
C.该企业老年职工绿色出行的人数和青年职工绿色出行的人数之和与中年职工绿色出行的人数相等
D.该企业绿色出行的人数占总人数的80%
10.从含有false件正品false件次品的false件产品中,任意取2件产品,这2件产品中至少有一件次品的概率为( )
A.false B.false C.false D.false
11.某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,…,599,600,从中抽取60个样本,下面提供随机数表的第5行到第6行:
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号是( )
A.522 B.348 C.535 D.578
12.根据如下样本数据,得到的回归方程为y=a+bx,则( )
x
2
3
4
5
6
y
4
2.5
-0.5
-2
-3
A.a>0,b>o B.a>0,b<0 C.a<0,b>0 D.a<0,b<0
13.从装有两个白球和两个黄球的口袋中任取2个球,以下给出了四组事件:
①至少有1个白球与至少有1个黄球; ②至少有1个黄球与都是黄球;
③恰有1个白球与恰有1个黄球; ④恰有1个白球与都是黄球.
其中互斥而不对立的事件共有( )
A.0组 B.1组 C.2组 D.3组
14.某景区在开放时间内,每个整点时会有一趟观光车从景区入口发车,某人上午到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为( )
A.false B.false C.false D.false
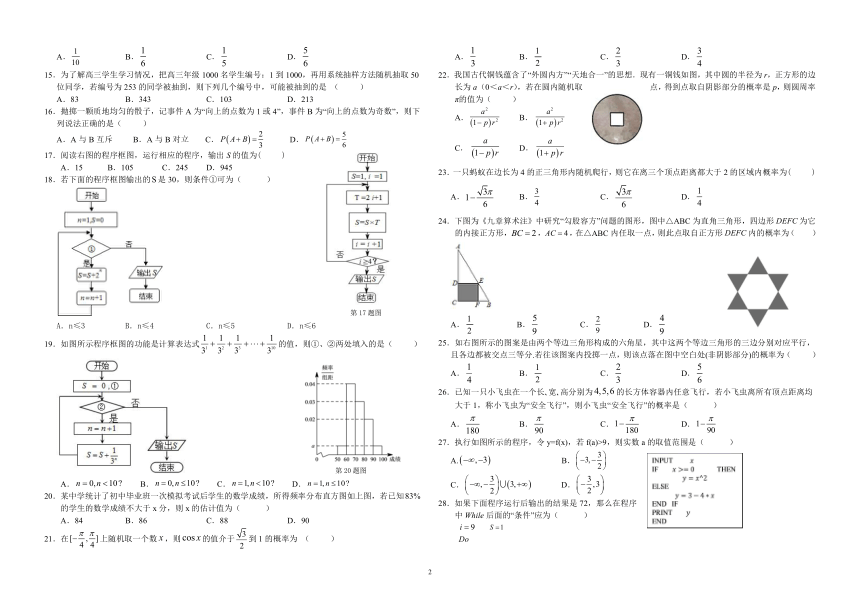
15.为了解高三学生学习情况,把高三年级1000名学生编号:1到1000,再用系统抽样方法随机抽取50位同学,若编号为253的同学被抽到,则下列几个编号中,可能被抽到的是 ( )
A.83 B.343 C.103 D.213
16.抛掷一颗质地均匀的骰子,记事件A为“向上的点数为1或4”,事件B为“向上的点数为奇数”,则下列说法正确的是( )
A.A与B互斥 B.A与B对立 C.false D.false
4473575381017.阅读右图的程序框图,运行相应的程序,输出S的值为( )
A.15 B.105 C.245 D.945
18.若下面的程序框图输出的false是30,则条件①可为( )
48844201918335第17题图
第17题图
A.n≤3 B.n≤4 C.n≤5 D.n≤6
19.如图所示程序框图的功能是计算表达式false的值,则①、②两处填入的是( )
46431201716405第20题图
第20题图
4203700128270
A.false B.false C.false D.false
20.某中学统计了初中毕业班一次模拟考试后学生的数学成绩,所得频率分布直方图如上图,若已知false 的学生的数学成绩不大于x分,则x的估计值为( )
A.84 B.86 C.88 D.90
21.在false上随机取一个数false,则false的值介于false到1的概率为 ( )
A.false B.false C.false D.false
22.我国古代铜钱蕴含了“外圆内方”“天地合一”的思想.现有一铜钱如图,其中圆的半径为r,正方形的边长为a(0<a<r),若在圆内随机取点,得到点取自阴影部分的概率是p,则圆周率π的值为( )
2491105-63500A.false B.false
C.false D.false
23.一只蚂蚁在边长为4的正三角形内随机爬行,则它在离三个顶点距离都大于2的区域内概率为( )
A.false B.false C.false D.false
24.下图为《九章算术注》中研究“勾股容方”问题的图形,图中△ABC为直角三角形,四边形false为它的内接正方形,false,false,在△ABC内任取一点,则此点取自正方形false内的概率为( )
4661535236855
A.false B.false C.false D.false
25.如右图所示的图案是由两个等边三角形构成的六角星,其中这两个等边三角形的三边分别对应平行,且各边都被交点三等分.若往该图案内投掷一点,则该点落在图中空白处(非阴影部分)的概率为( )
A.false B.false C.false D.false
26.已知一只小飞虫在一个长?宽?高分别为false的长方体容器内任意飞行,若小飞虫离所有顶点距离均大于1,称小飞虫为“安全飞行”,则小飞虫“安全飞行”的概率是( )
A.false B.false C.false D.false
27.执行如图所示的程序,令y=f(x),若f(a)>9,则实数a的取值范围是( )
339979083820A.false B.false
C.false D.false
28.如果下面程序运行后输出的结果是72,那么在程序
中While后面的“条件”应为( )
false false
Do
false
false
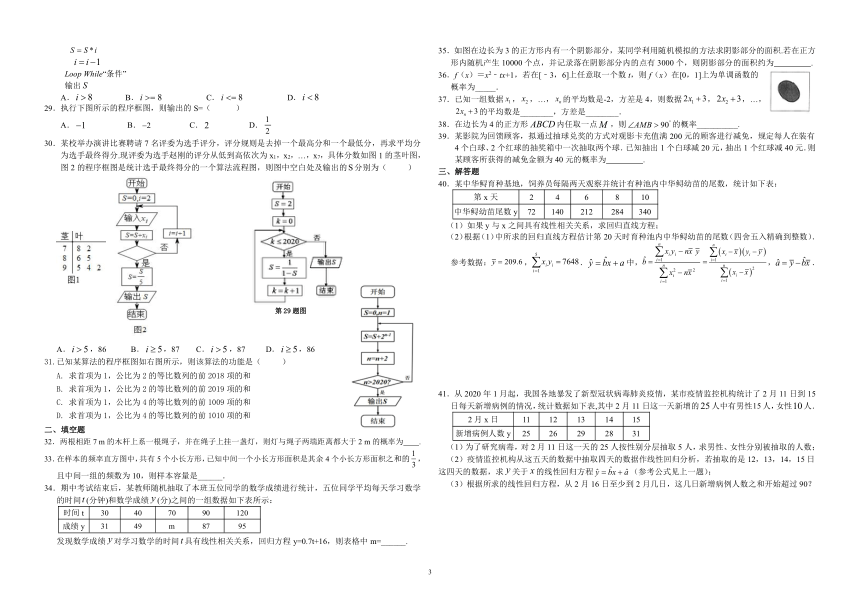
Loop While“条件”
输出false
A.false B.false C.false D.false
29.执行下图所示的程序框图,则输出的S=( )
A.false B.false C.false D.false
30.某校举办演讲比赛聘请7名评委为选手评分,评分规则是去掉一个最高分和一个最低分,再求平均分为选手最终得分.现评委为选手赵刚的评分从低到高依次为x1,x2,…,x7,具体分数如图1的茎叶图,图2的程序框图是统计选手最终得分的一个算法流程图,则图中空白处及输出的false分别为( )
4986020180784536588702083435第29题图
第29题图
339026592710
false,86 B.false,87 C.false,87 D.false,86
31.已知某算法的程序框图如右图所示,则该算法的功能是( )
A. 求首项为1,公比为2的等比数列的前2018项的和
B. 求首项为1,公比为2的等比数列的前2019项的和
C. 求首项为1,公比为4的等比数列的前1009项的和
D. 求首项为1,公比为4的等比数列的前1010项的和
二、填空题
32.两根相距7 m的木杆上系一根绳子,并在绳子上挂一盏灯,则灯与绳子两端距离都大于2 m的概率为 .
33.在样本的频率直方图中,共有5个小长方形,已知中间一个小长方形面积是其余4个小长方形面积之和的false,
且中间一组的频数为10,则样本容量是______.
34.期中考试结束后,某教师随机抽取了本班五位同学的数学成绩进行统计,五位同学平均每天学习数学的时间false(分钟)和数学成绩false(分)之间的一组数据如下表所示:
时间t
30
40
70
90
120
成绩y
31
49
m
87
95
发现数学成绩false对学习数学的时间false具有线性相关关系,回归方程y=0.7t+16,则表格中m=______.
35.如图在边长为3的正方形内有一个阴影部分,某同学利用随机模拟的方法求阴影部分的面积.若在正方形内随机产生10000个点,并记录落在阴影部分内的点有3000个,则阴影部分的面积约为 .
53898802984536.f(x)=x2﹣tx+1,若在[﹣3,6]上任意取一个数t,则f(x)在[0,1]上为单调函数的
概率为_____.
37.已知一组数据false,false,…,false的平均数是-2,方差是4,则数据false,false,…,false的平均数是________,方差是________.
38.在边长为4的正方形false内任取一点false,则false的概率__________.
39.某影院为回馈顾客,拟通过抽球兑奖的方式对观影卡充值满200元的顾客进行减免,规定每人在装有4个白球、2个红球的抽奖箱中一次抽取两个球.已知抽出1个白球减20元,抽出1个红球减40元.则某顾客所获得的减免金额为40元的概率为 .
三、解答题
40.某中华鲟育种基地,饲养员每隔两天观察并统计有种池内中华鲟幼苗的尾数,统计如下表:
第x天
2
4
6
8
10
中华鲟幼苗尾数y
72
140
212
284
340
(1)如果y与x之间具有线性相关关系,求回归直线方程;
(2)根据(1)中所求的回归直线方程估计第20天时育种池内中华鲟幼苗的尾数(四舍五入精确到整数).
参考数据:false,false.false中,falsefalse,false.
41.从2020年1月起,我国各地暴发了新型冠状病毒肺炎疫情,某市疫情监控机构统计了2月11日到15日每天新增病例的情况,统计数据如下表,其中2月11日这一天新增的false人中有男性false人,女性false人.
2月x日
11
12
13
14
15
新增病例人数y
25
26
29
28
31
(1)为了研究病毒,对2月11日这一天的25人按性别分层抽取5人,求男性、女性分别被抽取的人数;
(2)疫情监控机构从这五天的数据中抽取四天的数据作线性回归分析,若抽取的是12,13,14,15日这四天的数据,求false关于false的线性回归方程false(参考公式见上一题);
(3)根据所求的线性回归方程,从2月16日至少到2月几日,这几日新增病例人数之和开始超过90?
42.一个不透明的袋子中装有5个小球,其中有3个红球,2个白球,这些球除颜色外完全相同.
(1)记事件A为“一次摸出2个球,摸出的球为一个红球,一个白球”.求P(A);
(2)记事件B为“第一次摸出一个球,记下颜色后将它放回袋中,再摸出一个球,两次摸出的球颜色不同”,记事件C为“第一次摸出一个球,不放回袋中,再次摸出一个球,两次摸出的球颜色不同”,求P(B)和P(C).
43.袋中有9个大小相同颜色不全相同的小球,分别为黑球?黄球?绿球,从中任意取一球,得到黑球或黄
球的概率是false,得到黄球或绿球的概率是false,试求:
从中任取一球,得到黑球?黄球?绿球的概率各是多少?
(2)从中任取两个球,得到的两个球颜色不相同的概率是多少?
44.某机构从全体高一学生中抽取部分学生参加体育测试,按照测试成绩绘制茎叶图,并以false,false,false,false,false为分组做出频率分布直方图,后来茎叶图受到了污损,可见部分信息如下.
(1)求参加体育测试的人数false,及频率分布直方图中false的值;
(2)从分数在false,false的学生中随机选取2人进行调查,求至少1人分散在false的频率.
4667250546103238500116840
45.为了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照false分为5组,其频率分布直方图如图所示.
(1)求图中a的值;
(2)估计这些果实重量的平均数false,和方差false(同一组中的数据用该组区间的中点值作代表);
3849370353060(3)已知这种植物果实重量不低于32.5克的即为优质果实.若所取样本容量false,从该样本分布在false和false的果实中,随机抽取2个,求抽到的都是优质果实的概率
永丰中学2020-2021学年高一下学期6月月考数学答案(必修3)
1.D 2.C 3.A 4.D
由题意得false,①,false,②
由①②解得false或false,所以|x-y|=18.
5.A 6.C
解:时速的众数的估计值为falsekm/h.前两个矩形的面积为(0.01+0.03)×10=0.4.
∵0.5-0.4=0.1,false,∴中位数的估计值为60+2.5=62.5(km/h).
7.C 8.D 9.D 10.A
11.D
根据题意,依次获取的样本编号为:436,535,577,348,522,578,…故第6个样本编号是578.
12.B
false随着false的增大而减小,确定false,由图表中的数据可得,变量false随着false的增大而减小,则false,
false,false,又回归方程y=a+bx经过点false,可得a>0,
13.B 14.B
15.D 用系统抽样的方法随机抽取50位同学,可得组距为false,
16.C 17.B
18.B
循环前,false,false,
第1次判断后循环,false,false,
第2次判断并循环,false,false,
第3次判断并循环,false,false,
第4次判断并循环,false,false,
第5次判断不满足条件①并退出循环,输出false.false条件①应该是n≤4或false
19.A
①处应填false,这样第一次循环后false,若填false,第一次循环后false,不满足
②处应填false,最后输出的结果才是false
20.A
由频率分布直方图知false,解得false.
前三组的频率之和为false,
而前四组的频率之和为false,
false由false,解得false,即false的估计值为false.
21.C
根据题意,在区间false上,由false,解得false,false,
22.A pfalse1false,所以πfalse.
23.A
满足条件的正false如下图所示:
其中正false的面积为false,阴影部分区域的面积为false.
则使取到的点到三个顶点false、false、false的距离都大于false的概率是false.
24.D
解:false,false,false,解得false,
false,false,根据几何概型false.
25.B
设这两个等边三角形的边长为false,
依题意可知,图案中false个黑色三角形都是边长为false的等边三角形,空白处是边长为false的正六边形,因此该点落在图中空白处(非阴影部分)的概率为false.
26.D
因为false均大于false,所以小飞虫在每一个顶点附近的不完全区域不重合,而小飞虫不安全飞行区
域为false个半径为false的false的球体,所以小飞虫“安全飞行”的概率是false,
27.C
因为false所以由false,得false或false解得false或false.
故实数false的取值范围是false
28.B
计数变量i的初始值为9,累积变量S的初始值为1,第1次循环后得S=9,i=8.
因为9≠72,故执行第2次循环,得false,i=7,满足false,退出循环.结合选项,所以“条件”应为i≥8.
29.D
第一次循环,false成立,false,false;
第二次循环,false成立,false,false;
第三次循环,false成立,false,false;
第四次循环,false成立,false,false;
由上可知,该算法循环是周期循环,且周期为false,
依次类推,执行最后一次循环,false成立,且false,此时false,
false,false不成立,跳出循环体,输出false的值为false.
30.C
由于需要去掉一个最高分,所以false只能取到6,故空白处的条件应是false,
由于该算法的功能是求去掉一个最高分和一个最低分之后的平均分,false.
31.D 32.false 33.40 34.63 35.2.7
36.false
false对称轴为false,false在false上单调,所以false或false,解得false或false,
故false或false,故所求概率为false,故答案为:false.
-1 false
38.false
如图,正方形的边长为4,以AB为直径的半圆.
当false落在半圆内时,false;当false落在半圆上时,false;当false落在半圆外时,false.
故使false的概率false
39.设4个白球为a,b,c,d,2个红球为e,f,事件A为顾客所获得的减免金额为40元,
则一共可抽取false共15种情况,
false,共6种情况, 所以顾客所获得的减免金额为40元的概率为false.
40.(1)由题可知false,false,false,false,
false,false,false回归直线方程为false.
(2)false,即第false天时育种池中中华鲟幼苗大约有false尾.
41.(1)按性别分层抽取false名,则男性被抽取的人数为false,女性被抽取的人数为false.
(2)由题可知false,false,
false,false,
所以false关于false的线性回归方程为false
(3)由(2)可知,当false时,false,
当false时,false,当false时,false,
因为false,false,
所以从2月16日至少到2月18日,这三日新增病例人数之和开始超过false.
42.解:(1)记这3个红球为false,2个白球记为false,
则从袋中一次摸出2个球的所有基本事件为:false,false,false,false,false,false,
false,false,false,false共10个,其中满足事件false的基本事件有6个,所以false.
从袋中第一次摸出一个球,记下颜色后将它放回袋中,再次摸出一个球的所有基本事件为false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,
false,false共25个,满足事件false的基本事件有12个,所以false.
从袋中第一次摸出一个球,不放回袋中,再次摸出一个球的所有基本事件为false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false共20个,满足事件false的基本事件有12个,所
以false.
43.(1)从中任取一球,分别记得到黑球?黄球?绿球为事件false,false,C,由于false,false,C为互斥事件,
则false,得false,任取一球,得到黑球?黄球?绿球的概率分别是false,false,false.
(2)由(1)知黑球?黄球?绿球个数分别为3,2,4,
从9个球中取出2个球的样本空间中共有36个样本点,
其中两个是黑球的样本点是3个,两个黄球的是1个,两个绿球的是6个,
于是,两个球同色的概率为false,则两个球颜色不相同的概率是false.
44.(1) 测试成绩位于false的频数为false,频率为false,所以false,
测试成绩位于false的频率等于测试成绩位于false的频率为false,
所以测试成绩位于false的有false人,测试成绩位于false,false,false有false人,
所以测试成绩位于false有false人,所以false,
(2)由(1)知分数在false的有false人分别记为false,分数在false的有false人记为false,
从中随机取false人基本事件有:false共false个,
至少1人分散在false的基本事件有false共false个,
所以至少1人分散在false的频率为false.
45.(1)组距false,由false,得false.
(2)false,
false.
由已知,果实重量在false和false内的分别有4个和3个,分别记为false和false从中任取2个的取法有:false,
false,false,
共21种取法,其中都是优质果实的取法有B1B2,B1B3,B2B3,所以抽到的都是优质果实的概率false
数学试卷(必修3)
★查漏补缺,积极备考,再创辉煌!
一、选择题
1.某中学进行了该学年度期末统一考试,该校为了了解高一年级1000名学生的考试成绩,从中随机抽取了100名学生的成绩,就这个问题来说,下面说法正确的是( )
A.1000名学生是总体 B.每个学生是个体
C.1000名学生的成绩是一个个体 D.样本的容量是100
2.人民礼堂有50排座位,每排有60个座位号,一次报告会坐满了听众,会后留下座位号为18的所有听众50人进行座谈,这是运用了( )
A.抽签法 B.随机数法 C.系统抽样 D.放回抽样
3.给出下列4个说法:①概率为0的事件是不可能事件;②若某种彩票的中奖概率为false,则购买1000张彩票至少有一张中奖;③在一次随机试验中,任何两个基本事件都是对立事件;④两个互斥事件的概率之和等于1.其中正确说法的个数是( )
A.0 B.1 C.2 D.3
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为x,y,105,109,110.已知她的五次数学成绩数据的平均数为108分,方差为35.2,则|x-y|的值为( )
A.15 B.16 C.17 D.18
5.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A.false B.false C.false D.false
6.200辆汽车通过某一段公路时时速的频率分布直方图如图,则时速的众数、中位数的估计值为( )
A.62 km/h,62.5 km/h B.65 km/h,62 km/h C.65 km/h,62.5 km/h D.62.5 km/h,62.5 km/h
7.连抛两次骰子,以先后得到的点数m,n为P(m,n))坐标,那么点P在圆false内部的概率是( )
A.false B.false C.false D.false
8.某赛季甲?乙两名篮球运动员13场比赛得分情况用茎叶图表示如下:根据茎叶图,对这两名运动员的成绩进行比较,下列结论不正确的是( )
A.甲运动员得分的极差大于乙运动员的极差 B.甲运动员得分的中位数大于乙运动员的中位数
C.甲运动员得分的平均值大于乙运动员的平均值 D.甲运动员的成绩比乙运动员的成绩稳定
9.某企业有职工80000人,其职工年龄情况和绿色出行情况如下图,则正确的是( )
753745936625中年职工
中年职工
A.该企业老年职工绿色出行的人数最多 B.该企业青年职工绿色出行的人数最多
C.该企业老年职工绿色出行的人数和青年职工绿色出行的人数之和与中年职工绿色出行的人数相等
D.该企业绿色出行的人数占总人数的80%
10.从含有false件正品false件次品的false件产品中,任意取2件产品,这2件产品中至少有一件次品的概率为( )
A.false B.false C.false D.false
11.某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,…,599,600,从中抽取60个样本,下面提供随机数表的第5行到第6行:
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号是( )
A.522 B.348 C.535 D.578
12.根据如下样本数据,得到的回归方程为y=a+bx,则( )
x
2
3
4
5
6
y
4
2.5
-0.5
-2
-3
A.a>0,b>o B.a>0,b<0 C.a<0,b>0 D.a<0,b<0
13.从装有两个白球和两个黄球的口袋中任取2个球,以下给出了四组事件:
①至少有1个白球与至少有1个黄球; ②至少有1个黄球与都是黄球;
③恰有1个白球与恰有1个黄球; ④恰有1个白球与都是黄球.
其中互斥而不对立的事件共有( )
A.0组 B.1组 C.2组 D.3组
14.某景区在开放时间内,每个整点时会有一趟观光车从景区入口发车,某人上午到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为( )
A.false B.false C.false D.false
15.为了解高三学生学习情况,把高三年级1000名学生编号:1到1000,再用系统抽样方法随机抽取50位同学,若编号为253的同学被抽到,则下列几个编号中,可能被抽到的是 ( )
A.83 B.343 C.103 D.213
16.抛掷一颗质地均匀的骰子,记事件A为“向上的点数为1或4”,事件B为“向上的点数为奇数”,则下列说法正确的是( )
A.A与B互斥 B.A与B对立 C.false D.false
4473575381017.阅读右图的程序框图,运行相应的程序,输出S的值为( )
A.15 B.105 C.245 D.945
18.若下面的程序框图输出的false是30,则条件①可为( )
48844201918335第17题图
第17题图
A.n≤3 B.n≤4 C.n≤5 D.n≤6
19.如图所示程序框图的功能是计算表达式false的值,则①、②两处填入的是( )
46431201716405第20题图
第20题图
4203700128270
A.false B.false C.false D.false
20.某中学统计了初中毕业班一次模拟考试后学生的数学成绩,所得频率分布直方图如上图,若已知false 的学生的数学成绩不大于x分,则x的估计值为( )
A.84 B.86 C.88 D.90
21.在false上随机取一个数false,则false的值介于false到1的概率为 ( )
A.false B.false C.false D.false
22.我国古代铜钱蕴含了“外圆内方”“天地合一”的思想.现有一铜钱如图,其中圆的半径为r,正方形的边长为a(0<a<r),若在圆内随机取点,得到点取自阴影部分的概率是p,则圆周率π的值为( )
2491105-63500A.false B.false
C.false D.false
23.一只蚂蚁在边长为4的正三角形内随机爬行,则它在离三个顶点距离都大于2的区域内概率为( )
A.false B.false C.false D.false
24.下图为《九章算术注》中研究“勾股容方”问题的图形,图中△ABC为直角三角形,四边形false为它的内接正方形,false,false,在△ABC内任取一点,则此点取自正方形false内的概率为( )
4661535236855
A.false B.false C.false D.false
25.如右图所示的图案是由两个等边三角形构成的六角星,其中这两个等边三角形的三边分别对应平行,且各边都被交点三等分.若往该图案内投掷一点,则该点落在图中空白处(非阴影部分)的概率为( )
A.false B.false C.false D.false
26.已知一只小飞虫在一个长?宽?高分别为false的长方体容器内任意飞行,若小飞虫离所有顶点距离均大于1,称小飞虫为“安全飞行”,则小飞虫“安全飞行”的概率是( )
A.false B.false C.false D.false
27.执行如图所示的程序,令y=f(x),若f(a)>9,则实数a的取值范围是( )
339979083820A.false B.false
C.false D.false
28.如果下面程序运行后输出的结果是72,那么在程序
中While后面的“条件”应为( )
false false
Do
false
false
Loop While“条件”
输出false
A.false B.false C.false D.false
29.执行下图所示的程序框图,则输出的S=( )
A.false B.false C.false D.false
30.某校举办演讲比赛聘请7名评委为选手评分,评分规则是去掉一个最高分和一个最低分,再求平均分为选手最终得分.现评委为选手赵刚的评分从低到高依次为x1,x2,…,x7,具体分数如图1的茎叶图,图2的程序框图是统计选手最终得分的一个算法流程图,则图中空白处及输出的false分别为( )
4986020180784536588702083435第29题图
第29题图
339026592710
false,86 B.false,87 C.false,87 D.false,86
31.已知某算法的程序框图如右图所示,则该算法的功能是( )
A. 求首项为1,公比为2的等比数列的前2018项的和
B. 求首项为1,公比为2的等比数列的前2019项的和
C. 求首项为1,公比为4的等比数列的前1009项的和
D. 求首项为1,公比为4的等比数列的前1010项的和
二、填空题
32.两根相距7 m的木杆上系一根绳子,并在绳子上挂一盏灯,则灯与绳子两端距离都大于2 m的概率为 .
33.在样本的频率直方图中,共有5个小长方形,已知中间一个小长方形面积是其余4个小长方形面积之和的false,
且中间一组的频数为10,则样本容量是______.
34.期中考试结束后,某教师随机抽取了本班五位同学的数学成绩进行统计,五位同学平均每天学习数学的时间false(分钟)和数学成绩false(分)之间的一组数据如下表所示:
时间t
30
40
70
90
120
成绩y
31
49
m
87
95
发现数学成绩false对学习数学的时间false具有线性相关关系,回归方程y=0.7t+16,则表格中m=______.
35.如图在边长为3的正方形内有一个阴影部分,某同学利用随机模拟的方法求阴影部分的面积.若在正方形内随机产生10000个点,并记录落在阴影部分内的点有3000个,则阴影部分的面积约为 .
53898802984536.f(x)=x2﹣tx+1,若在[﹣3,6]上任意取一个数t,则f(x)在[0,1]上为单调函数的
概率为_____.
37.已知一组数据false,false,…,false的平均数是-2,方差是4,则数据false,false,…,false的平均数是________,方差是________.
38.在边长为4的正方形false内任取一点false,则false的概率__________.
39.某影院为回馈顾客,拟通过抽球兑奖的方式对观影卡充值满200元的顾客进行减免,规定每人在装有4个白球、2个红球的抽奖箱中一次抽取两个球.已知抽出1个白球减20元,抽出1个红球减40元.则某顾客所获得的减免金额为40元的概率为 .
三、解答题
40.某中华鲟育种基地,饲养员每隔两天观察并统计有种池内中华鲟幼苗的尾数,统计如下表:
第x天
2
4
6
8
10
中华鲟幼苗尾数y
72
140
212
284
340
(1)如果y与x之间具有线性相关关系,求回归直线方程;
(2)根据(1)中所求的回归直线方程估计第20天时育种池内中华鲟幼苗的尾数(四舍五入精确到整数).
参考数据:false,false.false中,falsefalse,false.
41.从2020年1月起,我国各地暴发了新型冠状病毒肺炎疫情,某市疫情监控机构统计了2月11日到15日每天新增病例的情况,统计数据如下表,其中2月11日这一天新增的false人中有男性false人,女性false人.
2月x日
11
12
13
14
15
新增病例人数y
25
26
29
28
31
(1)为了研究病毒,对2月11日这一天的25人按性别分层抽取5人,求男性、女性分别被抽取的人数;
(2)疫情监控机构从这五天的数据中抽取四天的数据作线性回归分析,若抽取的是12,13,14,15日这四天的数据,求false关于false的线性回归方程false(参考公式见上一题);
(3)根据所求的线性回归方程,从2月16日至少到2月几日,这几日新增病例人数之和开始超过90?
42.一个不透明的袋子中装有5个小球,其中有3个红球,2个白球,这些球除颜色外完全相同.
(1)记事件A为“一次摸出2个球,摸出的球为一个红球,一个白球”.求P(A);
(2)记事件B为“第一次摸出一个球,记下颜色后将它放回袋中,再摸出一个球,两次摸出的球颜色不同”,记事件C为“第一次摸出一个球,不放回袋中,再次摸出一个球,两次摸出的球颜色不同”,求P(B)和P(C).
43.袋中有9个大小相同颜色不全相同的小球,分别为黑球?黄球?绿球,从中任意取一球,得到黑球或黄
球的概率是false,得到黄球或绿球的概率是false,试求:
从中任取一球,得到黑球?黄球?绿球的概率各是多少?
(2)从中任取两个球,得到的两个球颜色不相同的概率是多少?
44.某机构从全体高一学生中抽取部分学生参加体育测试,按照测试成绩绘制茎叶图,并以false,false,false,false,false为分组做出频率分布直方图,后来茎叶图受到了污损,可见部分信息如下.
(1)求参加体育测试的人数false,及频率分布直方图中false的值;
(2)从分数在false,false的学生中随机选取2人进行调查,求至少1人分散在false的频率.
4667250546103238500116840
45.为了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照false分为5组,其频率分布直方图如图所示.
(1)求图中a的值;
(2)估计这些果实重量的平均数false,和方差false(同一组中的数据用该组区间的中点值作代表);
3849370353060(3)已知这种植物果实重量不低于32.5克的即为优质果实.若所取样本容量false,从该样本分布在false和false的果实中,随机抽取2个,求抽到的都是优质果实的概率
永丰中学2020-2021学年高一下学期6月月考数学答案(必修3)
1.D 2.C 3.A 4.D
由题意得false,①,false,②
由①②解得false或false,所以|x-y|=18.
5.A 6.C
解:时速的众数的估计值为falsekm/h.前两个矩形的面积为(0.01+0.03)×10=0.4.
∵0.5-0.4=0.1,false,∴中位数的估计值为60+2.5=62.5(km/h).
7.C 8.D 9.D 10.A
11.D
根据题意,依次获取的样本编号为:436,535,577,348,522,578,…故第6个样本编号是578.
12.B
false随着false的增大而减小,确定false,由图表中的数据可得,变量false随着false的增大而减小,则false,
false,false,又回归方程y=a+bx经过点false,可得a>0,
13.B 14.B
15.D 用系统抽样的方法随机抽取50位同学,可得组距为false,
16.C 17.B
18.B
循环前,false,false,
第1次判断后循环,false,false,
第2次判断并循环,false,false,
第3次判断并循环,false,false,
第4次判断并循环,false,false,
第5次判断不满足条件①并退出循环,输出false.false条件①应该是n≤4或false
19.A
①处应填false,这样第一次循环后false,若填false,第一次循环后false,不满足
②处应填false,最后输出的结果才是false
20.A
由频率分布直方图知false,解得false.
前三组的频率之和为false,
而前四组的频率之和为false,
false由false,解得false,即false的估计值为false.
21.C
根据题意,在区间false上,由false,解得false,false,
22.A pfalse1false,所以πfalse.
23.A
满足条件的正false如下图所示:
其中正false的面积为false,阴影部分区域的面积为false.
则使取到的点到三个顶点false、false、false的距离都大于false的概率是false.
24.D
解:false,false,false,解得false,
false,false,根据几何概型false.
25.B
设这两个等边三角形的边长为false,
依题意可知,图案中false个黑色三角形都是边长为false的等边三角形,空白处是边长为false的正六边形,因此该点落在图中空白处(非阴影部分)的概率为false.
26.D
因为false均大于false,所以小飞虫在每一个顶点附近的不完全区域不重合,而小飞虫不安全飞行区
域为false个半径为false的false的球体,所以小飞虫“安全飞行”的概率是false,
27.C
因为false所以由false,得false或false解得false或false.
故实数false的取值范围是false
28.B
计数变量i的初始值为9,累积变量S的初始值为1,第1次循环后得S=9,i=8.
因为9≠72,故执行第2次循环,得false,i=7,满足false,退出循环.结合选项,所以“条件”应为i≥8.
29.D
第一次循环,false成立,false,false;
第二次循环,false成立,false,false;
第三次循环,false成立,false,false;
第四次循环,false成立,false,false;
由上可知,该算法循环是周期循环,且周期为false,
依次类推,执行最后一次循环,false成立,且false,此时false,
false,false不成立,跳出循环体,输出false的值为false.
30.C
由于需要去掉一个最高分,所以false只能取到6,故空白处的条件应是false,
由于该算法的功能是求去掉一个最高分和一个最低分之后的平均分,false.
31.D 32.false 33.40 34.63 35.2.7
36.false
false对称轴为false,false在false上单调,所以false或false,解得false或false,
故false或false,故所求概率为false,故答案为:false.
-1 false
38.false
如图,正方形的边长为4,以AB为直径的半圆.
当false落在半圆内时,false;当false落在半圆上时,false;当false落在半圆外时,false.
故使false的概率false
39.设4个白球为a,b,c,d,2个红球为e,f,事件A为顾客所获得的减免金额为40元,
则一共可抽取false共15种情况,
false,共6种情况, 所以顾客所获得的减免金额为40元的概率为false.
40.(1)由题可知false,false,false,false,
false,false,false回归直线方程为false.
(2)false,即第false天时育种池中中华鲟幼苗大约有false尾.
41.(1)按性别分层抽取false名,则男性被抽取的人数为false,女性被抽取的人数为false.
(2)由题可知false,false,
false,false,
所以false关于false的线性回归方程为false
(3)由(2)可知,当false时,false,
当false时,false,当false时,false,
因为false,false,
所以从2月16日至少到2月18日,这三日新增病例人数之和开始超过false.
42.解:(1)记这3个红球为false,2个白球记为false,
则从袋中一次摸出2个球的所有基本事件为:false,false,false,false,false,false,
false,false,false,false共10个,其中满足事件false的基本事件有6个,所以false.
从袋中第一次摸出一个球,记下颜色后将它放回袋中,再次摸出一个球的所有基本事件为false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,
false,false共25个,满足事件false的基本事件有12个,所以false.
从袋中第一次摸出一个球,不放回袋中,再次摸出一个球的所有基本事件为false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false共20个,满足事件false的基本事件有12个,所
以false.
43.(1)从中任取一球,分别记得到黑球?黄球?绿球为事件false,false,C,由于false,false,C为互斥事件,
则false,得false,任取一球,得到黑球?黄球?绿球的概率分别是false,false,false.
(2)由(1)知黑球?黄球?绿球个数分别为3,2,4,
从9个球中取出2个球的样本空间中共有36个样本点,
其中两个是黑球的样本点是3个,两个黄球的是1个,两个绿球的是6个,
于是,两个球同色的概率为false,则两个球颜色不相同的概率是false.
44.(1) 测试成绩位于false的频数为false,频率为false,所以false,
测试成绩位于false的频率等于测试成绩位于false的频率为false,
所以测试成绩位于false的有false人,测试成绩位于false,false,false有false人,
所以测试成绩位于false有false人,所以false,
(2)由(1)知分数在false的有false人分别记为false,分数在false的有false人记为false,
从中随机取false人基本事件有:false共false个,
至少1人分散在false的基本事件有false共false个,
所以至少1人分散在false的频率为false.
45.(1)组距false,由false,得false.
(2)false,
false.
由已知,果实重量在false和false内的分别有4个和3个,分别记为false和false从中任取2个的取法有:false,
false,false,
共21种取法,其中都是优质果实的取法有B1B2,B1B3,B2B3,所以抽到的都是优质果实的概率false
同课章节目录
