七年级数学三角形内角和定理
文档属性
| 名称 | 七年级数学三角形内角和定理 |  | |
| 格式 | zip | ||
| 文件大小 | 157.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-11 20:31:17 | ||
图片预览


文档简介
(共38张PPT)
1、三角形的内角和是多少度?
2、我们学习的哪些图形是180度?
平角(或邻补角)
平行线形成的同旁内角
3、请你构建平角或同旁内角,结合所学平行线知识来证明三角形内角和定理
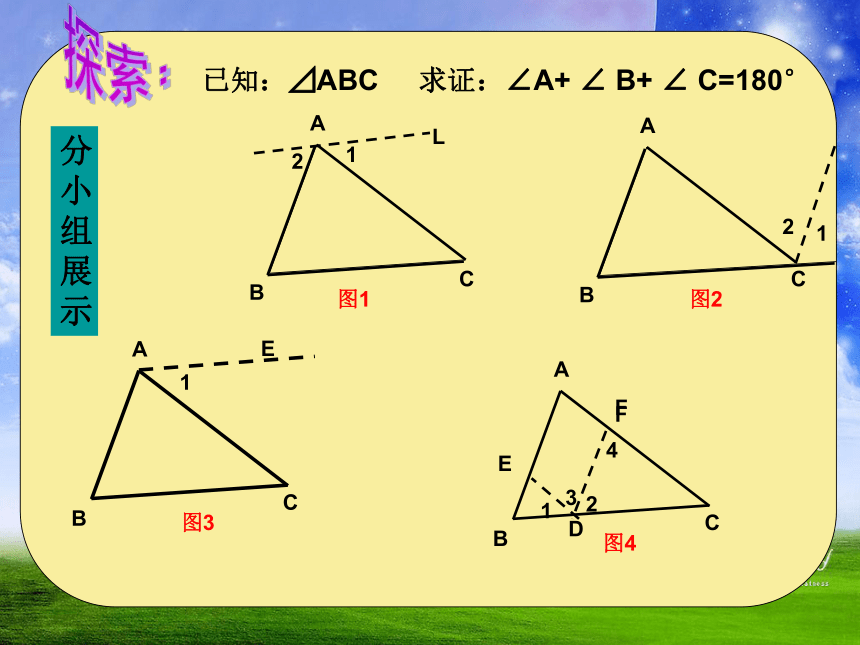
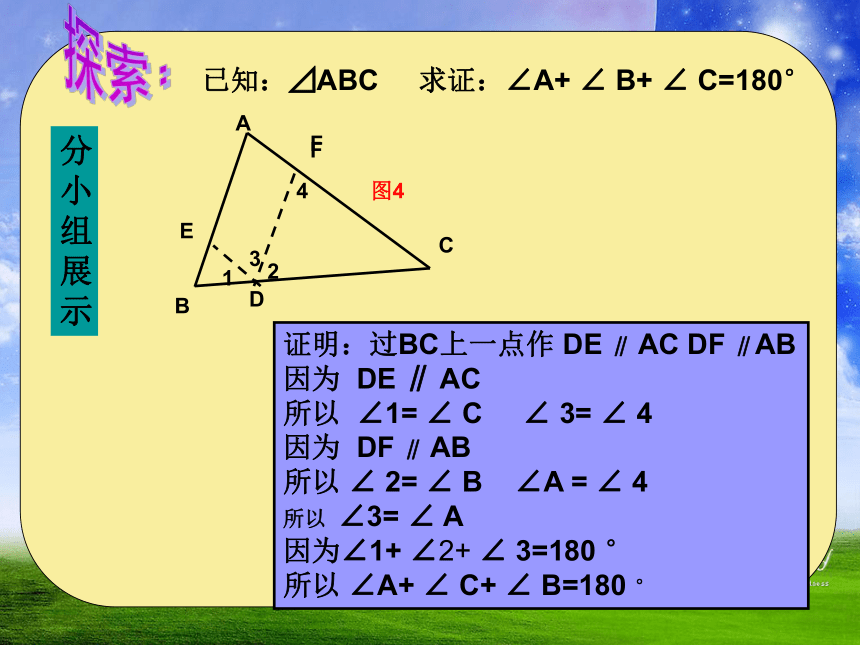
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
C
图2
L
A
B
图1
1
2
C
2
1
A
B
图3
C
1
E
A
B
图4
C
D
4
3
2
1
F
F
E
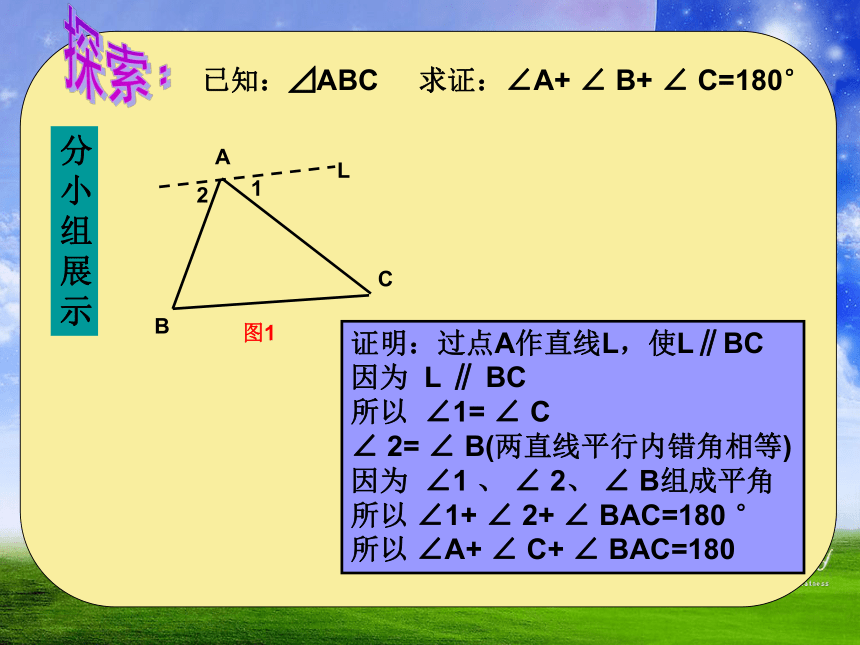
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
C
L
A
B
图1
1
2
证明:过点A作直线L,使L∥BC
因为 L ∥ BC
所以 ∠1= ∠ C
∠ 2= ∠ B(两直线平行内错角相等)
因为 ∠1 、 ∠ 2、 ∠ B组成平角
所以 ∠1+ ∠ 2+ ∠ BAC=180 °
所以 ∠A+ ∠ C+ ∠ BAC=180
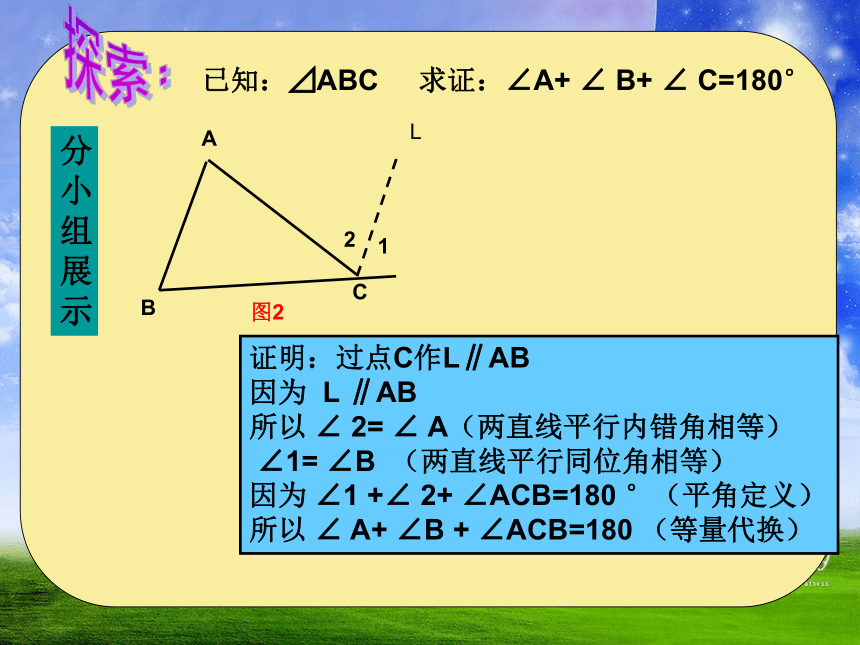
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
图2
C
2
1
证明:过点C作L∥AB
因为 L ∥AB
所以 ∠ 2= ∠ A(两直线平行内错角相等)
∠1= ∠B (两直线平行同位角相等)
因为 ∠1 +∠ 2+ ∠ACB=180 °(平角定义)
所以 ∠ A+ ∠B + ∠ACB=180 (等量代换)
L
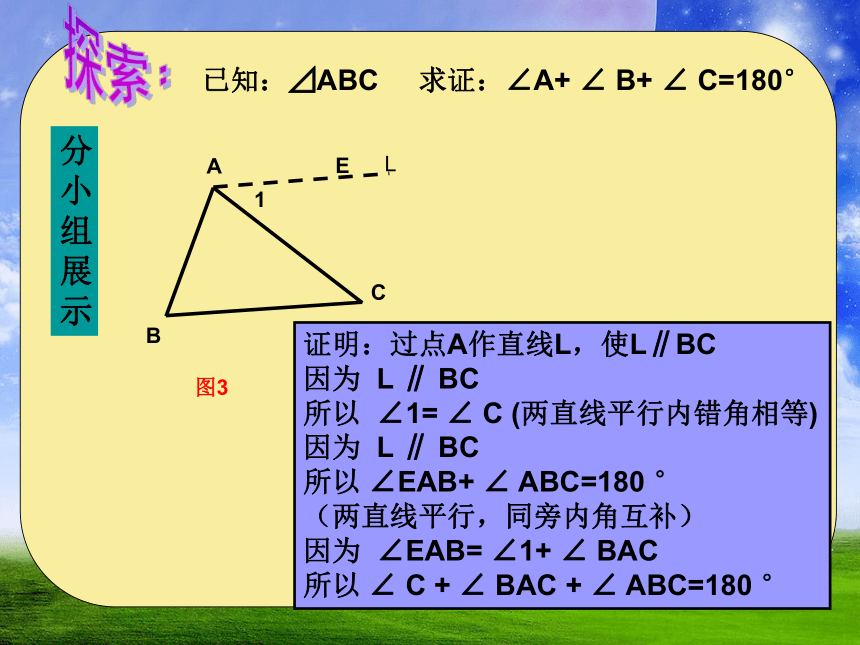
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
图3
C
1
E
L
证明:过点A作直线L,使L∥BC
因为 L ∥ BC
所以 ∠1= ∠ C (两直线平行内错角相等)
因为 L ∥ BC
所以 ∠EAB+ ∠ ABC=180 °
(两直线平行,同旁内角互补)
因为 ∠EAB= ∠1+ ∠ BAC
所以 ∠ C + ∠ BAC + ∠ ABC=180 °
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
图4
C
D
4
3
2
1
F
F
E
证明:过BC上一点作 DE ∥ AC DF ∥AB
因为 DE ∥ AC
所以 ∠1= ∠ C ∠ 3= ∠ 4
因为 DF ∥ AB
所以 ∠ 2= ∠ B ∠A = ∠ 4
所以 ∠3= ∠ A
因为∠1+ ∠2+ ∠ 3=180 °
所以 ∠A+ ∠ C+ ∠ B=180 °
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
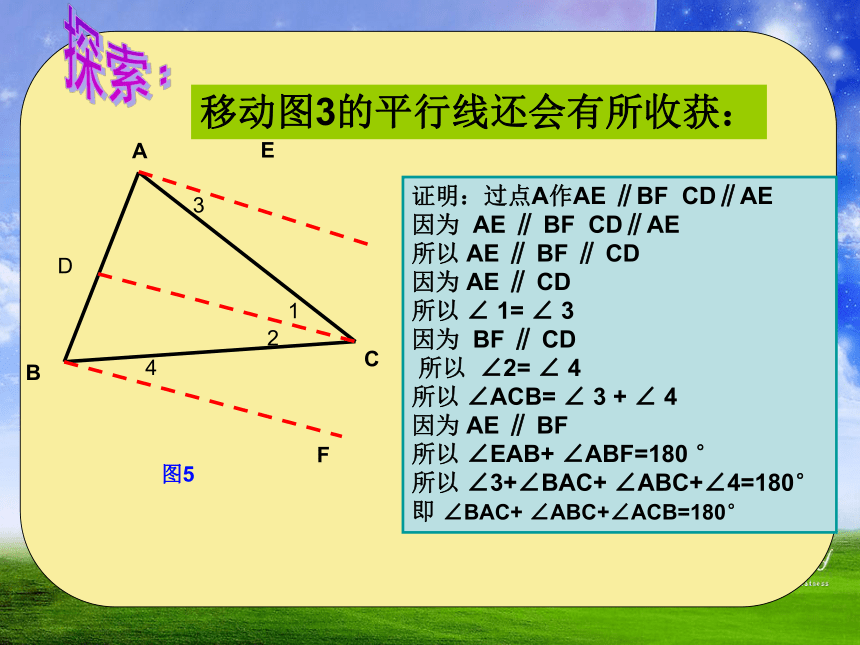
F
D
1
2
3
4
图5
证明:过点A作AE ∥BF CD∥AE
因为 AE ∥ BF CD∥AE
所以 AE ∥ BF ∥ CD
因为 AE ∥ CD
所以 ∠ 1= ∠ 3
因为 BF ∥ CD
所以 ∠2= ∠ 4
所以 ∠ACB= ∠ 3 + ∠ 4
因为 AE ∥ BF
所以 ∠EAB+ ∠ABF=180 °
所以 ∠3+∠BAC+ ∠ABC+∠4=180°
即 ∠BAC+ ∠ABC+∠ACB=180°
A
B
C
E
移动图3的平行线还会有所收获:
F
2
1
3
证明:过点C作CE∥AB EF∥BC 交AB于点F
因为 AB ∥CE
所以 ∠1= ∠ A ∠2= ∠ 3
因为 AB ∥ CE
所以 ∠B=∠2 ∠3+ ∠ BCE =180 °
所以 ∠B=∠3
所以 ∠B + ∠ACB + ∠A=180 °
图6
构造平角或平行线所截的同旁内角,再利用平行线知识将各角转换到图形中,使问题得证。
1、三角形的内角和是多少度?
2、我们学习的哪些图形是180度?
平角(或邻补角)
平行线形成的同旁内角
3、请你构建平角或同旁内角,结合所学平行线知识来证明三角形内角和定理
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
C
图2
L
A
B
图1
1
2
C
2
1
A
B
图3
C
1
E
A
B
图4
C
D
4
3
2
1
F
F
E
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
C
L
A
B
图1
1
2
证明:过点A作直线L,使L∥BC
因为 L ∥ BC
所以 ∠1= ∠ C
∠ 2= ∠ B(两直线平行内错角相等)
因为 ∠1 、 ∠ 2、 ∠ B组成平角
所以 ∠1+ ∠ 2+ ∠ BAC=180 °
所以 ∠A+ ∠ C+ ∠ BAC=180
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
图2
C
2
1
证明:过点C作L∥AB
因为 L ∥AB
所以 ∠ 2= ∠ A(两直线平行内错角相等)
∠1= ∠B (两直线平行同位角相等)
因为 ∠1 +∠ 2+ ∠ACB=180 °(平角定义)
所以 ∠ A+ ∠B + ∠ACB=180 (等量代换)
L
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
图3
C
1
E
L
证明:过点A作直线L,使L∥BC
因为 L ∥ BC
所以 ∠1= ∠ C (两直线平行内错角相等)
因为 L ∥ BC
所以 ∠EAB+ ∠ ABC=180 °
(两直线平行,同旁内角互补)
因为 ∠EAB= ∠1+ ∠ BAC
所以 ∠ C + ∠ BAC + ∠ ABC=180 °
已知:⊿ABC 求证:∠A+ ∠ B+ ∠ C=180°
分
小
组
展
示
A
B
图4
C
D
4
3
2
1
F
F
E
证明:过BC上一点作 DE ∥ AC DF ∥AB
因为 DE ∥ AC
所以 ∠1= ∠ C ∠ 3= ∠ 4
因为 DF ∥ AB
所以 ∠ 2= ∠ B ∠A = ∠ 4
所以 ∠3= ∠ A
因为∠1+ ∠2+ ∠ 3=180 °
所以 ∠A+ ∠ C+ ∠ B=180 °
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
A
B
C
E
移动图3的平行线还会有所收获:
F
D
1
2
3
4
图5
证明:过点A作AE ∥BF CD∥AE
因为 AE ∥ BF CD∥AE
所以 AE ∥ BF ∥ CD
因为 AE ∥ CD
所以 ∠ 1= ∠ 3
因为 BF ∥ CD
所以 ∠2= ∠ 4
所以 ∠ACB= ∠ 3 + ∠ 4
因为 AE ∥ BF
所以 ∠EAB+ ∠ABF=180 °
所以 ∠3+∠BAC+ ∠ABC+∠4=180°
即 ∠BAC+ ∠ABC+∠ACB=180°
A
B
C
E
移动图3的平行线还会有所收获:
F
2
1
3
证明:过点C作CE∥AB EF∥BC 交AB于点F
因为 AB ∥CE
所以 ∠1= ∠ A ∠2= ∠ 3
因为 AB ∥ CE
所以 ∠B=∠2 ∠3+ ∠ BCE =180 °
所以 ∠B=∠3
所以 ∠B + ∠ACB + ∠A=180 °
图6
构造平角或平行线所截的同旁内角,再利用平行线知识将各角转换到图形中,使问题得证。
