2020--2021学年人教版(五四制 )八年级数学下册综合测试试题(Word版含答案)
文档属性
| 名称 | 2020--2021学年人教版(五四制 )八年级数学下册综合测试试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 241.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 14:22:30 | ||
图片预览


文档简介
八年级数学数学综合测试测试试卷
一、选择题(每小题3分,共计30分)
1.下列关于x的方程是一元二次方程的是( )
A.x3﹣3x+8=0 B.x2+y﹣3=0 C.+x=2 D.3x(x﹣4)=0
2.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是 ( ).
A.60° B.90° C.120° D.45°
3.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等
4.一次函数y=kx+b的图象经过第一、三、四象限,则(? )
A.?k>0,b>0???B.?k>0,b<0??C.?k<0,b>0??D.?k<0,b<0
5.用配方法解下列方程,其中应在两端同时加上4的是( )
A. B. C. D.
6.对于函数 ,下列说法不正确的是(?? )
A.?其图象经过点(0,0)??????B.?其图象经过点(﹣1, )
C.?其图象经过第二、四象限?????D.?y随x的增大而增大
7.学生冬季运动装原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是( )
A.9% B. 8.5% C. 9.5% D.10%
8.点P1(x1,y1),点P2(x2,y2)是一次函数y =-4x + 3 图象上的两个点,且 x1<x2,则y1与y2的大小关系是( ).
A、y1>y2 B、y1<y2 C、y1=y2 D、 无法确定
9.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. 2.5 B. C. D. 2
10.甲乙两人在一条笔直的公路上从A地步行去往B地.已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离y(千米)与甲步行的时间t(小时)的函数关系图象如图所示,下列说法:①乙的速度为7千米/小时;②乙到终点时甲、乙相距8千米;③当乙追上甲时,两人距A地21千米④A、B两地距离为35千米,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计30分)
11. 函数,则自变量x的取值范围是_________.
12.分解因式:ax?-4a = .
13.已知直角三角形的两直角边长分别为5和12,则其斜边中线长为________.
14.已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高为__________.
15.已知直线与直线相交于一点,则该点的坐标是 .
16. 已知关于x的一元二次方程x2+2x+k=0有两个相等的实数根,则k= .
17. 市工会组织篮球比赛庆五一,赛制为单循环形式(每两队之间都赛一场),共进行了36场比赛,则这次参加比赛的球队个数为__________.
18. 如图,函数y=x+2b和y=ax+3的图象交于点P,则不等式x+2b>ax+3的解集为__________.
19. △ABC中,AB=AC=5,BC=6,点M在直线BC上,且CM=1,则AM=______________.
20. 已知等腰Rt△ACB,∠ACB=90°,AC=BC,点F为BC上一点,过点B作BD⊥AF交AF延长线于点D,点E在AC上,连接BE,∠CBD=2∠ABE,若CF=5,AE=4,则AB=_________.
三、解答题(共计60分)
21.(本题7分)先化简,再求值: ÷ ,其中 m=-5.
22.(本题7分)
如图,每个小正方形的边长都是1的方格纸中,有线段AB和
线段CD,点A、B、C、D的端点都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AB为一边的菱形ABEF,所画的菱形的各顶点必须在小正方形的顶点上,并且其面积为20.
(2)在方格纸中以CD为底边画出等腰三角形CDK,点K在小正方形的顶点上,且△CDK的面积为5.
(3)连接FK,直接写出FK的长.
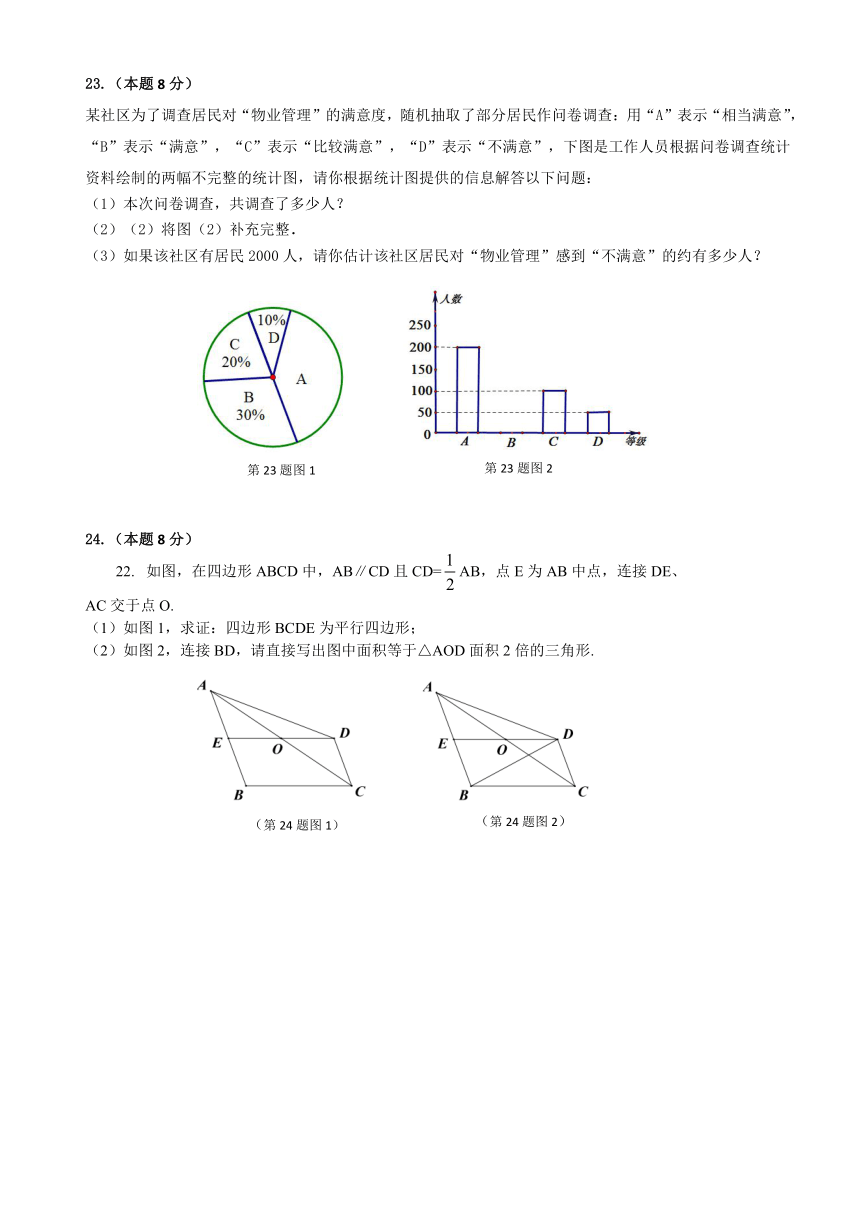
23.(本题8分)
某社区为了调查居民对“物业管理”的满意度,随机抽取了部分居民作问卷调查:用“A”表示“相当满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
本次问卷调查,共调查了多少人?
(2)将图(2)补充完整.
(3)如果该社区有居民2000人,请你估计该社区居民对“物业管理”感到“不满意”的约有多少人?
24.(本题8分)
如图,在四边形ABCD中,AB∥CD且CD=AB,点E为AB中点,连接DE、
AC交于点O.
(1)如图1,求证:四边形BCDE为平行四边形;
(2)如图2,连接BD,请直接写出图中面积等于△AOD面积2倍的三角形.
25.(本题10分)龙锐中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买2副围棋和1副中国象棋需用42元;若购买3副围棋和2副中国象棋需用68元.
(1)求每副围棋和每副中国象棋各多少元?
(2)龙锐中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么龙锐中学最多可以购买多少副围棋.
(本题10分)如图1,已知△ACB中,∠A=45°,AB=AC.
(1)如图1,求证:AC=BC;
(2)如图2,点D为AB的中点,点E在AC上,过点D作DF⊥DE交BC于点F,求证:S四边形CECF=S△ACB;
(3)如图3,在(2)的条件下,连接BE、EF,且∠EBC=2∠CEF,S△BEF=8,求AB长.
27.(本题10分)已知,在平面直角坐标系中,点O为坐标原点,直线AB与x轴的正半轴交于点A,与y轴的负半轴交于点B,OA=OB,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为,过点C作CM⊥y轴,垂足为M,OM=9.
(1)如图1,求直线AB的解析式;
(2)如图2,点N在线段MC上,连接ON,过ON上的点P作y轴的平行线交OC于点E,若MN:CN=3:5,且PE=2.5,求点P的坐标;
(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,GQ-FG=AF,连接PF,求PF的长.
答案
一、选择题:
1 2 3 4 5 6 7 8 9 10
D A C B C D D A B D
二、填空题:
11 12 13 14 15 16 17 18 19 20
X≠1 a(x+2)(x-2) 6.5 4.8 (-10,-24) 1 9 x>1 或
三、解答题:
21.
22.画图略FK=
23(1)500 (2)150 (3)200
24.证明略△AED,△BED,△BCD,△ACD
25.(1)围棋16元,中国象棋10元;(2)最多购买25副围棋
26.证明略⑶
27.(1)y=x-12 (2)P(2,4) (3)10
一、选择题(每小题3分,共计30分)
1.下列关于x的方程是一元二次方程的是( )
A.x3﹣3x+8=0 B.x2+y﹣3=0 C.+x=2 D.3x(x﹣4)=0
2.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是 ( ).
A.60° B.90° C.120° D.45°
3.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.对角线互相垂直 D.对角线相等
4.一次函数y=kx+b的图象经过第一、三、四象限,则(? )
A.?k>0,b>0???B.?k>0,b<0??C.?k<0,b>0??D.?k<0,b<0
5.用配方法解下列方程,其中应在两端同时加上4的是( )
A. B. C. D.
6.对于函数 ,下列说法不正确的是(?? )
A.?其图象经过点(0,0)??????B.?其图象经过点(﹣1, )
C.?其图象经过第二、四象限?????D.?y随x的增大而增大
7.学生冬季运动装原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是( )
A.9% B. 8.5% C. 9.5% D.10%
8.点P1(x1,y1),点P2(x2,y2)是一次函数y =-4x + 3 图象上的两个点,且 x1<x2,则y1与y2的大小关系是( ).
A、y1>y2 B、y1<y2 C、y1=y2 D、 无法确定
9.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. 2.5 B. C. D. 2
10.甲乙两人在一条笔直的公路上从A地步行去往B地.已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离y(千米)与甲步行的时间t(小时)的函数关系图象如图所示,下列说法:①乙的速度为7千米/小时;②乙到终点时甲、乙相距8千米;③当乙追上甲时,两人距A地21千米④A、B两地距离为35千米,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共计30分)
11. 函数,则自变量x的取值范围是_________.
12.分解因式:ax?-4a = .
13.已知直角三角形的两直角边长分别为5和12,则其斜边中线长为________.
14.已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高为__________.
15.已知直线与直线相交于一点,则该点的坐标是 .
16. 已知关于x的一元二次方程x2+2x+k=0有两个相等的实数根,则k= .
17. 市工会组织篮球比赛庆五一,赛制为单循环形式(每两队之间都赛一场),共进行了36场比赛,则这次参加比赛的球队个数为__________.
18. 如图,函数y=x+2b和y=ax+3的图象交于点P,则不等式x+2b>ax+3的解集为__________.
19. △ABC中,AB=AC=5,BC=6,点M在直线BC上,且CM=1,则AM=______________.
20. 已知等腰Rt△ACB,∠ACB=90°,AC=BC,点F为BC上一点,过点B作BD⊥AF交AF延长线于点D,点E在AC上,连接BE,∠CBD=2∠ABE,若CF=5,AE=4,则AB=_________.
三、解答题(共计60分)
21.(本题7分)先化简,再求值: ÷ ,其中 m=-5.
22.(本题7分)
如图,每个小正方形的边长都是1的方格纸中,有线段AB和
线段CD,点A、B、C、D的端点都在小正方形的顶点上.
(1)在方格纸中画出一个以线段AB为一边的菱形ABEF,所画的菱形的各顶点必须在小正方形的顶点上,并且其面积为20.
(2)在方格纸中以CD为底边画出等腰三角形CDK,点K在小正方形的顶点上,且△CDK的面积为5.
(3)连接FK,直接写出FK的长.
23.(本题8分)
某社区为了调查居民对“物业管理”的满意度,随机抽取了部分居民作问卷调查:用“A”表示“相当满意”,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,下图是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
本次问卷调查,共调查了多少人?
(2)将图(2)补充完整.
(3)如果该社区有居民2000人,请你估计该社区居民对“物业管理”感到“不满意”的约有多少人?
24.(本题8分)
如图,在四边形ABCD中,AB∥CD且CD=AB,点E为AB中点,连接DE、
AC交于点O.
(1)如图1,求证:四边形BCDE为平行四边形;
(2)如图2,连接BD,请直接写出图中面积等于△AOD面积2倍的三角形.
25.(本题10分)龙锐中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买2副围棋和1副中国象棋需用42元;若购买3副围棋和2副中国象棋需用68元.
(1)求每副围棋和每副中国象棋各多少元?
(2)龙锐中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么龙锐中学最多可以购买多少副围棋.
(本题10分)如图1,已知△ACB中,∠A=45°,AB=AC.
(1)如图1,求证:AC=BC;
(2)如图2,点D为AB的中点,点E在AC上,过点D作DF⊥DE交BC于点F,求证:S四边形CECF=S△ACB;
(3)如图3,在(2)的条件下,连接BE、EF,且∠EBC=2∠CEF,S△BEF=8,求AB长.
27.(本题10分)已知,在平面直角坐标系中,点O为坐标原点,直线AB与x轴的正半轴交于点A,与y轴的负半轴交于点B,OA=OB,过点A作x轴的垂线与过点O的直线相交于点C,直线OC的解析式为,过点C作CM⊥y轴,垂足为M,OM=9.
(1)如图1,求直线AB的解析式;
(2)如图2,点N在线段MC上,连接ON,过ON上的点P作y轴的平行线交OC于点E,若MN:CN=3:5,且PE=2.5,求点P的坐标;
(3)如图3,在(2)的条件下,点F为线段AB上一点,连接OF,过点F作OF的垂线交线段AC于点Q,连接BQ,过点F作x轴的平行线交BQ于点G,GQ-FG=AF,连接PF,求PF的长.
答案
一、选择题:
1 2 3 4 5 6 7 8 9 10
D A C B C D D A B D
二、填空题:
11 12 13 14 15 16 17 18 19 20
X≠1 a(x+2)(x-2) 6.5 4.8 (-10,-24) 1 9 x>1 或
三、解答题:
21.
22.画图略FK=
23(1)500 (2)150 (3)200
24.证明略△AED,△BED,△BCD,△ACD
25.(1)围棋16元,中国象棋10元;(2)最多购买25副围棋
26.证明略⑶
27.(1)y=x-12 (2)P(2,4) (3)10
同课章节目录
