第三章 代数式 3.2代数式第4课时 课件 冀教版数学七年级上册(共22张)
文档属性
| 名称 | 第三章 代数式 3.2代数式第4课时 课件 冀教版数学七年级上册(共22张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 18:24:34 | ||
图片预览






文档简介
(共22张PPT)
3.2
代数式
第三章
代数式
第4课时
用代数式表示规律
导入新课
这是某月的日历,你能发现日历中的数字有什么规律吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
问题引入
学习目标
1.能用代数式表示数或图形的变化规律;
2.
能够利用所学知识和方法解决相关规律探究类的问题.
讲授新课
用代数式表示数的变化规律
一
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1.请找出同一直线上相邻数之间的关系:
(1)横行三个相邻数的关系;
(2)竖列三个相邻数的关系.
后者比前者多1.
用代数式表示为:
a-1,a,a+1
下者比上者多7.
用代数式表示为:
b-7,b,b+7
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
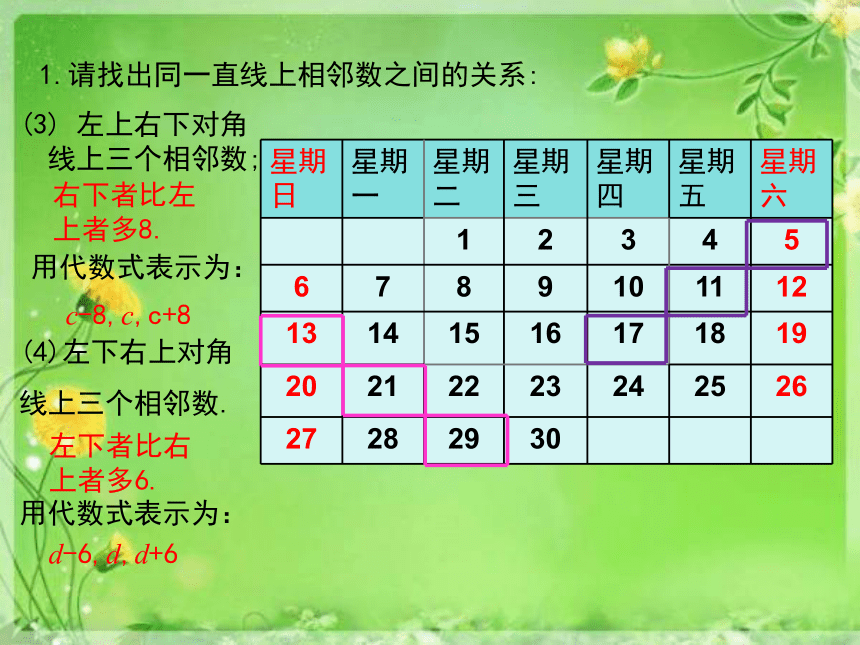
(3)
左上右下对角
线上三个相邻数;
(4)左下右上对角线上三个相邻数.
右下者比左
上者多8.
用代数式表示为:
c-8,c,c+8
左下者比右
上者多6.
用代数式表示为:
d-6,d,d+6
1.请找出同一直线上相邻数之间的关系:
a-1,a,a+1
(1)水平相邻的三个数
(2)竖直相邻的三个数
b-7,a,b+7
(3)斜下相邻的三个数
c-8,c,c+8
(4)斜上相邻的三个数
d-6,d,d+6
(a-1)+a+(a+1)=3a.
(b-7)+b+(b+7)=3b.
(c-8)+c+(c+8)=3c.
(d-6)+d+(d+6)=3d.
用代数式表示为:
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
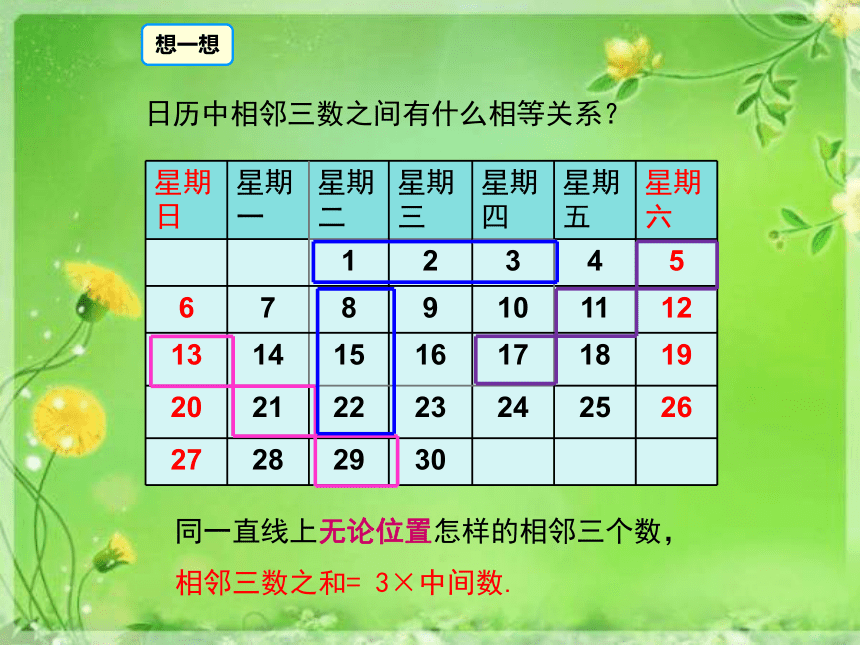
想一想
日历中相邻三数之间有什么相等关系?
同一直线上无论位置怎样的相邻三个数,
相邻三数之和=
3×中间数.
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2.日历中3×3方框内九数之和与方框中正中间的数有何等量关系?
2+3+4+9+10+11+16+17+18=90=9×10.
九数之和=9
×
中间数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
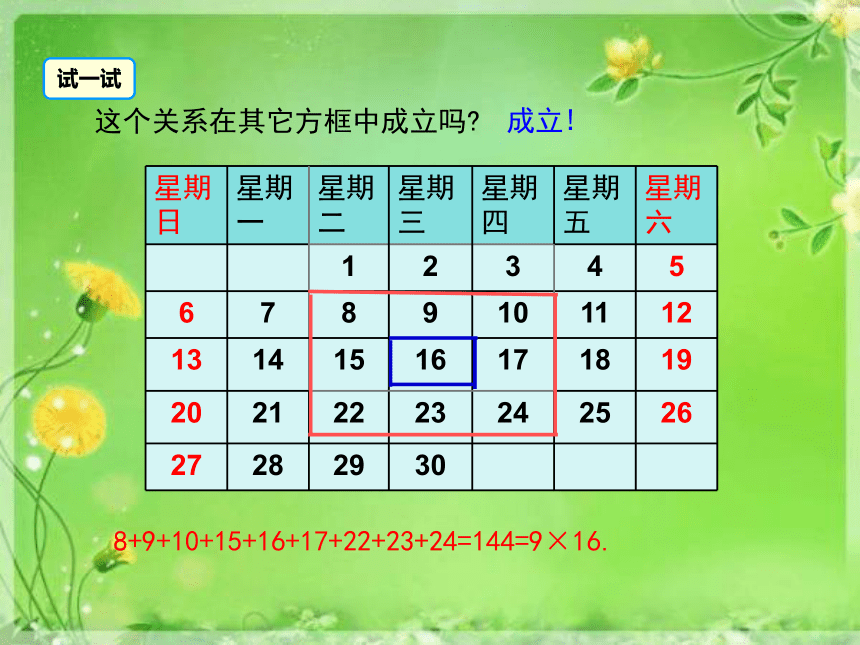
这个关系在其它方框中成立吗?
试一试
8+9+10+15+16+17+22+23+24=144=9×16.
成立!
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
验证你的猜想:
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)=9a
探索规律的一般步骤:
猜
想
规
律
表
示
规
律
验
证
规
律
具
体
问
题
观察、比较
成立
得出结论
头
回
新
重
索
探
归纳
例1
仔细观察下列各组数,按你发现的规律填空:
(1)
1,2,3,4,_____,______,第n个数是______.
(2)
2,4,6,8,______
,______,第n个数是______.
(3)
,______,_______,
第n个数是_____.
典例精析
5
6
n
10
12
2n
方法归纳
用代数式表示数的变化的规律:
(1)数字为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是奇、偶、平方等方面的规律;
(2)数字为分数,可分别观察分子、分母的变化规律及它们之间的联系;
…
…
…
…
一
二
三
四
4n-4
…
…
…
…
4(n-1)=4n-4
2n+2(n-2)=4n-4
…
…
…
…
用代数式表示图形的变化规律
二
用小棒按下图的方式搭三角形.
三角形
个数
1
2
3
4
5
…
n
小棒
根数
…
填写下表:
互动探究
3
+2
+2
+2
+2
+2
1+2
三角形个数
火柴棒根数
1
2
3
4
5
…
…
n
3=1+2
5=1+2+2
7=1+2+2+2
9=1+2+2+2+2
11=1+2+2+2+2+2
2n+1=1+2+2+2+2+
+2
课堂小结
用代数式表示规律
用代数式表示数的变化规律
用代数式表示图形的变化规律
3.2
代数式
第三章
代数式
第4课时
用代数式表示规律
导入新课
这是某月的日历,你能发现日历中的数字有什么规律吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
问题引入
学习目标
1.能用代数式表示数或图形的变化规律;
2.
能够利用所学知识和方法解决相关规律探究类的问题.
讲授新课
用代数式表示数的变化规律
一
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1.请找出同一直线上相邻数之间的关系:
(1)横行三个相邻数的关系;
(2)竖列三个相邻数的关系.
后者比前者多1.
用代数式表示为:
a-1,a,a+1
下者比上者多7.
用代数式表示为:
b-7,b,b+7
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
(3)
左上右下对角
线上三个相邻数;
(4)左下右上对角线上三个相邻数.
右下者比左
上者多8.
用代数式表示为:
c-8,c,c+8
左下者比右
上者多6.
用代数式表示为:
d-6,d,d+6
1.请找出同一直线上相邻数之间的关系:
a-1,a,a+1
(1)水平相邻的三个数
(2)竖直相邻的三个数
b-7,a,b+7
(3)斜下相邻的三个数
c-8,c,c+8
(4)斜上相邻的三个数
d-6,d,d+6
(a-1)+a+(a+1)=3a.
(b-7)+b+(b+7)=3b.
(c-8)+c+(c+8)=3c.
(d-6)+d+(d+6)=3d.
用代数式表示为:
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
想一想
日历中相邻三数之间有什么相等关系?
同一直线上无论位置怎样的相邻三个数,
相邻三数之和=
3×中间数.
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2.日历中3×3方框内九数之和与方框中正中间的数有何等量关系?
2+3+4+9+10+11+16+17+18=90=9×10.
九数之和=9
×
中间数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
这个关系在其它方框中成立吗?
试一试
8+9+10+15+16+17+22+23+24=144=9×16.
成立!
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
验证你的猜想:
(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7)+(a+8)=9a
探索规律的一般步骤:
猜
想
规
律
表
示
规
律
验
证
规
律
具
体
问
题
观察、比较
成立
得出结论
头
回
新
重
索
探
归纳
例1
仔细观察下列各组数,按你发现的规律填空:
(1)
1,2,3,4,_____,______,第n个数是______.
(2)
2,4,6,8,______
,______,第n个数是______.
(3)
,______,_______,
第n个数是_____.
典例精析
5
6
n
10
12
2n
方法归纳
用代数式表示数的变化的规律:
(1)数字为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是奇、偶、平方等方面的规律;
(2)数字为分数,可分别观察分子、分母的变化规律及它们之间的联系;
…
…
…
…
一
二
三
四
4n-4
…
…
…
…
4(n-1)=4n-4
2n+2(n-2)=4n-4
…
…
…
…
用代数式表示图形的变化规律
二
用小棒按下图的方式搭三角形.
三角形
个数
1
2
3
4
5
…
n
小棒
根数
…
填写下表:
互动探究
3
+2
+2
+2
+2
+2
1+2
三角形个数
火柴棒根数
1
2
3
4
5
…
…
n
3=1+2
5=1+2+2
7=1+2+2+2
9=1+2+2+2+2
11=1+2+2+2+2+2
2n+1=1+2+2+2+2+
+2
课堂小结
用代数式表示规律
用代数式表示数的变化规律
用代数式表示图形的变化规律
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
