21.3实际问题与一元二次方程---传播问题 课件(共22张PPT)
文档属性
| 名称 | 21.3实际问题与一元二次方程---传播问题 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
人教版
九年级数学上
21.3实际问题与一元二次方程
---传播问题
学习目标
1.会分析传播问题的数量关系并会列一元二次方程.(重点)
2.理解传播问题的传播过程,会找出传播问题的数量关系,建模
解决问题.(难点)
回顾旧知
1.
一元二次方程的解法有哪些?
①直接开平方法
②配方法
③公式法
④因式分解法
①审
②设
③找
④列
⑤解
⑥验
⑦答
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数量关系的数学模型。
本节课我们继续讨论如何利用一元二次方程解决实际问题。
2.列方程解题的一般步骤?
合作探究---传播问题
探究1:有一人患了流感,经过两轮传染后共有121人患了流感,每
轮传染中平均一个人传染了几个人?
启发思考:你知道传染病的传播速度是多快吗?
合作探究---传播问题
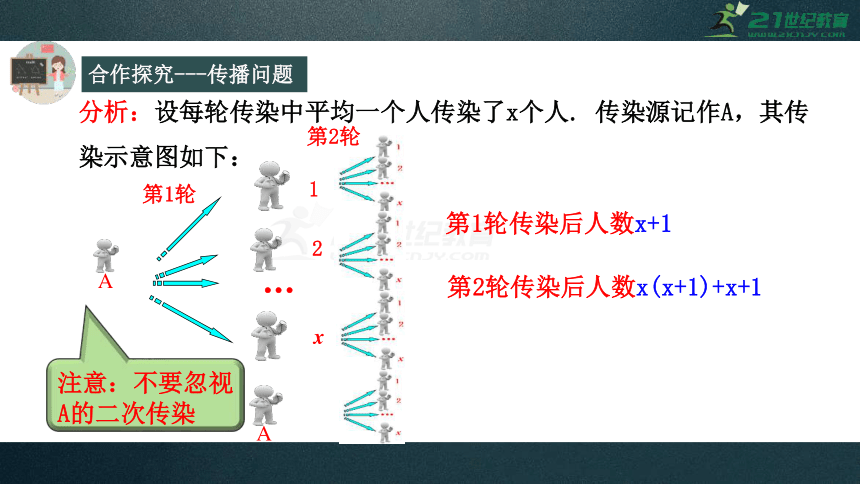
分析:设每轮传染中平均一个人传染了x个人.
传染源记作A,其传染示意图如下:
第2轮
???
A
1
2
x
第1轮
第1轮传染后人数x+1
A
第2轮传染后人数x(x+1)+x+1
注意:不要忽视A的二次传染
合作探究---传播问题
x1=
,
x2=
.
根据示意图,列表如下:
解方程,得
答:平均一个人传染了10个人.
10
-12
(不合题意,舍去)
解:设每轮传染中平均一个人传染了x个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
传染源人数
第1轮传染后的人数
第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
根据题意,得
合作探究---传播问题
思考:如果按照这样的传染速度,三轮传染后有多少人患流感?
第2种做法
以第2轮传染后的人数121为传染源,传染一次后就是:121(1+x)=121(1+10)=1331人.
第一轮传染后的人数
第二轮传染后的
人数
第三轮传染后的
人数
(1+x)1
(1+x)2
第1种做法
以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1331人.
(1+x)3
小试牛刀
1、新冠病毒的传染性极强,某地因2人患了新冠肺炎没有及时隔离治疗,经过两天的传染后共有50人患了新冠肺炎;问题:(1)每天平均一个人传染了几人?
解:设每天平均一个人传染了x人
即
(1+x)2
=25
解得
x
1=-6
(舍去),
x2=4.
答:每天平均一个人传染了4人。
则
2+2x+x(2+2x)=50
小试牛刀
(2)如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患新冠肺炎?
2(1+x)5
=2
(
1+4)7=156250
∴这个地区一共将会有156250人患新冠肺炎.
传染病的传播速度非常惊人!
归纳总结
传播问题:设传播前的量为a,传播速度为x,则:
第一轮传播后的量=a
×(1+x)
第二轮传播后的量=a×(1+x)2
第n轮传播后的量=a×(1+x)n
归纳:解决此类问题的关键步骤是:明确每轮传播中的传染源个数,
以及这一轮被传染的总数.
典例精析
例1
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则
1+x+x2=91
即x2+x-90=0
解得,
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
典例精析
例2.在陈老师所教的班级中,每两个学生都握手一次,全班学生一共握手780次,那么谁能计算出老师所教的班级共有多少名学生呢?
解:设李老师所教班共有x名学生,依题意有
即(x-40)(x+39)=0,
解得:x=40或x=-39(舍去).
故陈老师所教的班级共有40名学生.
典例精析
例3.一个两位数,十位数字比个位数字小3,个位数字的平方刚好等于这个两位数,则这个两位数是多少?
解:设这个两位数个位数字为
x
,则十位数字为(x-3),
根据题意得:
解得
x1=5,x2=6.
答:这个两位数是25或36.
∴x=5时,十位数字为2,x=6时,十位数字为3.
归纳总结
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检
验
运用一元二次方程模型解决实际问题的步骤有哪些?
综合演练
1.有一根绿萝,它的主干长出若干数目的
枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是68,设每个枝干长出x个小分支,根据题意可列方程为(
)
A.1+x+x(1+x)=68
B.1+x+x2=68
C.1+x2
=68
D.(1+x)2=68
B
2.元旦将至,九年级二班全体学生互赠贺卡,共赠贺卡2021张,问九年级二班共有多少名学生?设该共有x名学生,那么所列方程为(
)
A.x2=2021
B.
x(x+1)=2021
C.
D.x(x-1)=2021
D
综合演练
3.早期,甲肝流行,传染性很强,曾有2人同时患上甲肝.在一天内,一人平均能传染x人,经过两天传染后162人患上甲肝,则x的值为(
)
A.10
B.9
C.8
D.7
C
4.为了宣传环保,小明写了一篇倡议书,决定用微博转发的方式传播,他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请n个好友转发倡议书,每个好友转发倡议书之后,又邀请n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有133个人参与了传播活动,则n=______.
11
综合演练
5.某种电脑病毒传播的非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,若病毒得不到有效控制,三轮感染后,被感染的电脑有多少台?
解:设每轮感染中平均一台电脑会感染x台电脑.
81×9=729台
根据题意,得:(1+x)2=81;
解得:x1=8,x2=﹣10(不合题意,应舍去).
答:三轮感染后,被感染的电脑有729台.
综合演练
6.我校九年级各班进行篮球比赛(单循环制),每两班之间共比赛了15场,则九年级有几个班?
解:九年级有x个班,根据题意列方程,得
化简,得
x2-x-30=0
解方程,得
x1=6,
x2=-5(舍去)
答:九年级有6个班.
综合演练
7.某生物实验室需培育一群有益菌,现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
(1)每轮分裂中平均每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后共有多少个有益菌?
解:(1)设每个有益菌一次分裂出x个有益菌
60+60x+60(1+x)x=24000
x1=19,x2=-21(舍去)
∴每个有益菌一次分裂出19个有益菌.
(2)三轮后有益菌总数为
24000×(1+19)=480000(个).
课堂小结
本节课你有哪些收获?
1、解决传播问题时应注意的事项是什么?
2、解决传播问题的解题步骤是什么?
课后作业
教材21页习题21.3第2、3、6题.
https://www.21cnjy.com/help/help_extract.php
人教版
九年级数学上
21.3实际问题与一元二次方程
---传播问题
学习目标
1.会分析传播问题的数量关系并会列一元二次方程.(重点)
2.理解传播问题的传播过程,会找出传播问题的数量关系,建模
解决问题.(难点)
回顾旧知
1.
一元二次方程的解法有哪些?
①直接开平方法
②配方法
③公式法
④因式分解法
①审
②设
③找
④列
⑤解
⑥验
⑦答
同一元一次方程、二元一次方程(组)等一样,一元二次方程也可以作为反映某些实际问题中数量关系的数学模型。
本节课我们继续讨论如何利用一元二次方程解决实际问题。
2.列方程解题的一般步骤?
合作探究---传播问题
探究1:有一人患了流感,经过两轮传染后共有121人患了流感,每
轮传染中平均一个人传染了几个人?
启发思考:你知道传染病的传播速度是多快吗?
合作探究---传播问题
分析:设每轮传染中平均一个人传染了x个人.
传染源记作A,其传染示意图如下:
第2轮
???
A
1
2
x
第1轮
第1轮传染后人数x+1
A
第2轮传染后人数x(x+1)+x+1
注意:不要忽视A的二次传染
合作探究---传播问题
x1=
,
x2=
.
根据示意图,列表如下:
解方程,得
答:平均一个人传染了10个人.
10
-12
(不合题意,舍去)
解:设每轮传染中平均一个人传染了x个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
传染源人数
第1轮传染后的人数
第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
根据题意,得
合作探究---传播问题
思考:如果按照这样的传染速度,三轮传染后有多少人患流感?
第2种做法
以第2轮传染后的人数121为传染源,传染一次后就是:121(1+x)=121(1+10)=1331人.
第一轮传染后的人数
第二轮传染后的
人数
第三轮传染后的
人数
(1+x)1
(1+x)2
第1种做法
以1人为传染源,3轮传染后的人数是:
(1+x)3=(1+10)3=1331人.
(1+x)3
小试牛刀
1、新冠病毒的传染性极强,某地因2人患了新冠肺炎没有及时隔离治疗,经过两天的传染后共有50人患了新冠肺炎;问题:(1)每天平均一个人传染了几人?
解:设每天平均一个人传染了x人
即
(1+x)2
=25
解得
x
1=-6
(舍去),
x2=4.
答:每天平均一个人传染了4人。
则
2+2x+x(2+2x)=50
小试牛刀
(2)如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患新冠肺炎?
2(1+x)5
=2
(
1+4)7=156250
∴这个地区一共将会有156250人患新冠肺炎.
传染病的传播速度非常惊人!
归纳总结
传播问题:设传播前的量为a,传播速度为x,则:
第一轮传播后的量=a
×(1+x)
第二轮传播后的量=a×(1+x)2
第n轮传播后的量=a×(1+x)n
归纳:解决此类问题的关键步骤是:明确每轮传播中的传染源个数,
以及这一轮被传染的总数.
典例精析
例1
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支?
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则
1+x+x2=91
即x2+x-90=0
解得,
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
典例精析
例2.在陈老师所教的班级中,每两个学生都握手一次,全班学生一共握手780次,那么谁能计算出老师所教的班级共有多少名学生呢?
解:设李老师所教班共有x名学生,依题意有
即(x-40)(x+39)=0,
解得:x=40或x=-39(舍去).
故陈老师所教的班级共有40名学生.
典例精析
例3.一个两位数,十位数字比个位数字小3,个位数字的平方刚好等于这个两位数,则这个两位数是多少?
解:设这个两位数个位数字为
x
,则十位数字为(x-3),
根据题意得:
解得
x1=5,x2=6.
答:这个两位数是25或36.
∴x=5时,十位数字为2,x=6时,十位数字为3.
归纳总结
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检
验
运用一元二次方程模型解决实际问题的步骤有哪些?
综合演练
1.有一根绿萝,它的主干长出若干数目的
枝干,每个枝干又长出同样数目的小分支,主干、枝干、小分支的总数是68,设每个枝干长出x个小分支,根据题意可列方程为(
)
A.1+x+x(1+x)=68
B.1+x+x2=68
C.1+x2
=68
D.(1+x)2=68
B
2.元旦将至,九年级二班全体学生互赠贺卡,共赠贺卡2021张,问九年级二班共有多少名学生?设该共有x名学生,那么所列方程为(
)
A.x2=2021
B.
x(x+1)=2021
C.
D.x(x-1)=2021
D
综合演练
3.早期,甲肝流行,传染性很强,曾有2人同时患上甲肝.在一天内,一人平均能传染x人,经过两天传染后162人患上甲肝,则x的值为(
)
A.10
B.9
C.8
D.7
C
4.为了宣传环保,小明写了一篇倡议书,决定用微博转发的方式传播,他设计了如下的传播规则:将倡议书发表在自己的微博上,再邀请n个好友转发倡议书,每个好友转发倡议书之后,又邀请n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有133个人参与了传播活动,则n=______.
11
综合演练
5.某种电脑病毒传播的非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染,若病毒得不到有效控制,三轮感染后,被感染的电脑有多少台?
解:设每轮感染中平均一台电脑会感染x台电脑.
81×9=729台
根据题意,得:(1+x)2=81;
解得:x1=8,x2=﹣10(不合题意,应舍去).
答:三轮感染后,被感染的电脑有729台.
综合演练
6.我校九年级各班进行篮球比赛(单循环制),每两班之间共比赛了15场,则九年级有几个班?
解:九年级有x个班,根据题意列方程,得
化简,得
x2-x-30=0
解方程,得
x1=6,
x2=-5(舍去)
答:九年级有6个班.
综合演练
7.某生物实验室需培育一群有益菌,现有60个活体样本,经过两轮培植后,总和达24000个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
(1)每轮分裂中平均每个有益菌可分裂出多少个有益菌?
(2)按照这样的分裂速度,经过三轮培植后共有多少个有益菌?
解:(1)设每个有益菌一次分裂出x个有益菌
60+60x+60(1+x)x=24000
x1=19,x2=-21(舍去)
∴每个有益菌一次分裂出19个有益菌.
(2)三轮后有益菌总数为
24000×(1+19)=480000(个).
课堂小结
本节课你有哪些收获?
1、解决传播问题时应注意的事项是什么?
2、解决传播问题的解题步骤是什么?
课后作业
教材21页习题21.3第2、3、6题.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
