沪科版数学九年级上册期末达标检测卷(word版含答案)
文档属性
| 名称 | 沪科版数学九年级上册期末达标检测卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 433.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-18 23:04:46 | ||
图片预览



文档简介
沪科版数学九年级上册期末达标检测卷
一、选择题(每题4分,共40分)
1.已知a,d,c,b是成比例线段,其中a=3
cm,b=2
cm,c=6
cm,则d的长度为( )
A.4
cm
B.1
cm
C.9
cm
D.5
cm
2.在反比例函数y=图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k<0
B.k>0
C.k<1
D.k>1
3.对于抛物线y=-(x+2)2+3,有下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(-2,3);④当x>2时,y随x的增大而减小.其中正确结论的个数为( )
A.1
B.2
C.3
D.4
4.如图,在?ABCD中,E是AD边的中点,连接BE并延长交CD的延长线于点F,则△EDF与△BCF的周长之比是( )
A.1:2
B.1:3
C.1:4
D.1:5
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=,BC=2,则sin
∠ACD的值为( )
A.
B.
C.
D.
6.如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有( )
A.1对
B.2对
C.3对
D.4对
7.如图,在直角平面坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的相似比为的位似图形△OCD,则点C的坐标为( )
A.(-1,-1)
B.
C.
D.(-2,-1)
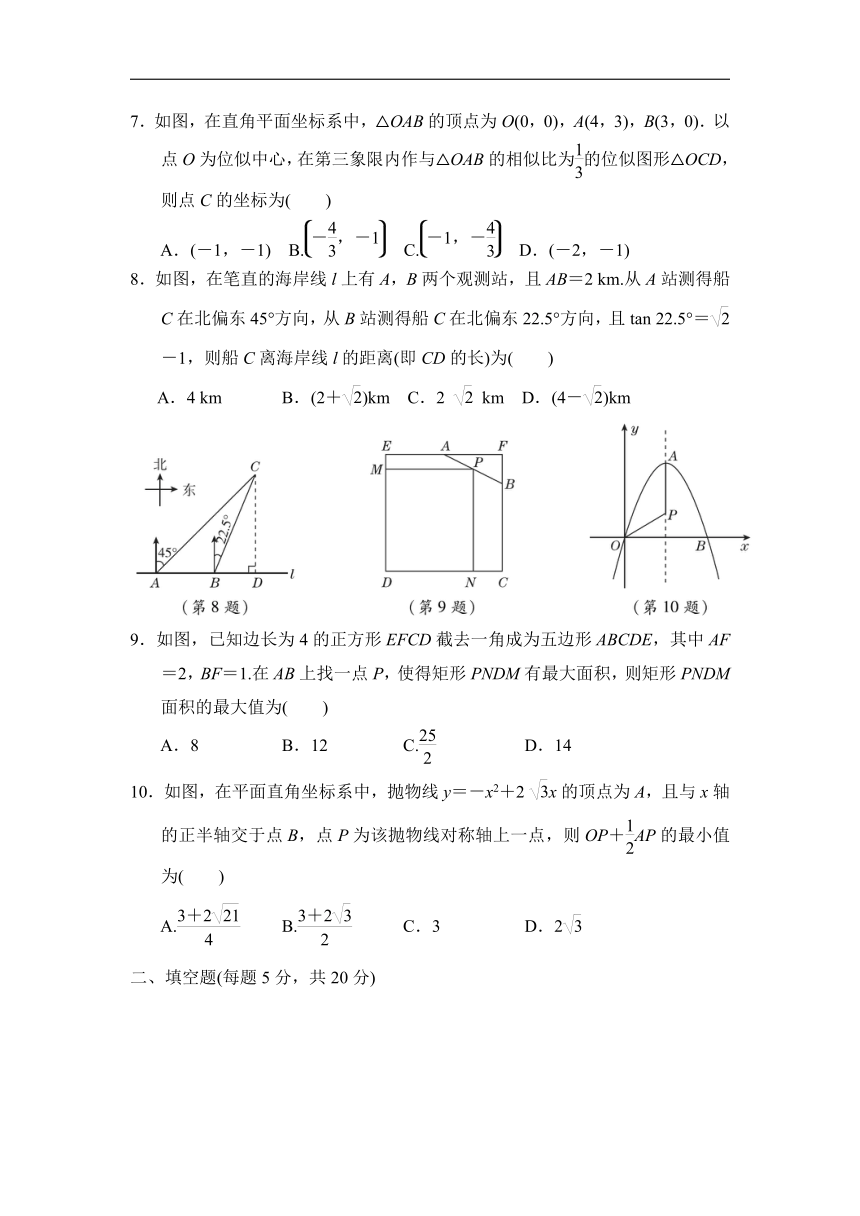
8.如图,在笔直的海岸线l上有A,B两个观测站,且AB=2
km.从A站测得船C在北偏东45°方向,从B站测得船C在北偏东22.5°方向,且tan
22.5°=-1,则船C离海岸线l的距离(即CD的长)为( )
A.4
km
B.(2+)km
C.2
km
D.(4-)km
9.如图,已知边长为4的正方形EFCD截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上找一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值为( )
A.8
B.12
C.
D.14
10.如图,在平面直角坐标系中,抛物线y=-x2+2
x的顶点为A,且与x轴的正半轴交于点B,点P为该抛物线对称轴上一点,则OP+AP的最小值为( )
A.
B.
C.3
D.2
二、填空题(每题5分,共20分)
11.如图,在由边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan
∠APD的值是________.
12.如图,点P是反比例函数y=(x>0)图象上一动点,在y轴上取点Q,使得以P,Q,O为顶点的三角形是含有30°角的直角三角形,则符合条件的点Q的坐标是________________.
13.如图是二次函数y=ax2+bx+c(a≠0)的图象,其与x轴的交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①abc>0;②4a-2b+c<0;③2a-b<0.其中正确的有____________(填序号).
14.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,使点C恰好落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,使点A恰好落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.其中正确的有____________(填序号).
三、解答题(15~18题每题8分;19,20题每题10分;21,22题每题12分;23题14分,共90分)
15.计算:(-1)2
022-6tan30°++|1-|.
16.已知抛物线y=x2-4x+7与直线y=x交于A,B两点(点A在点B左侧).
(1)求A,B两点的坐标;
(2)求抛物线顶点C的坐标,并求△ABC的面积.
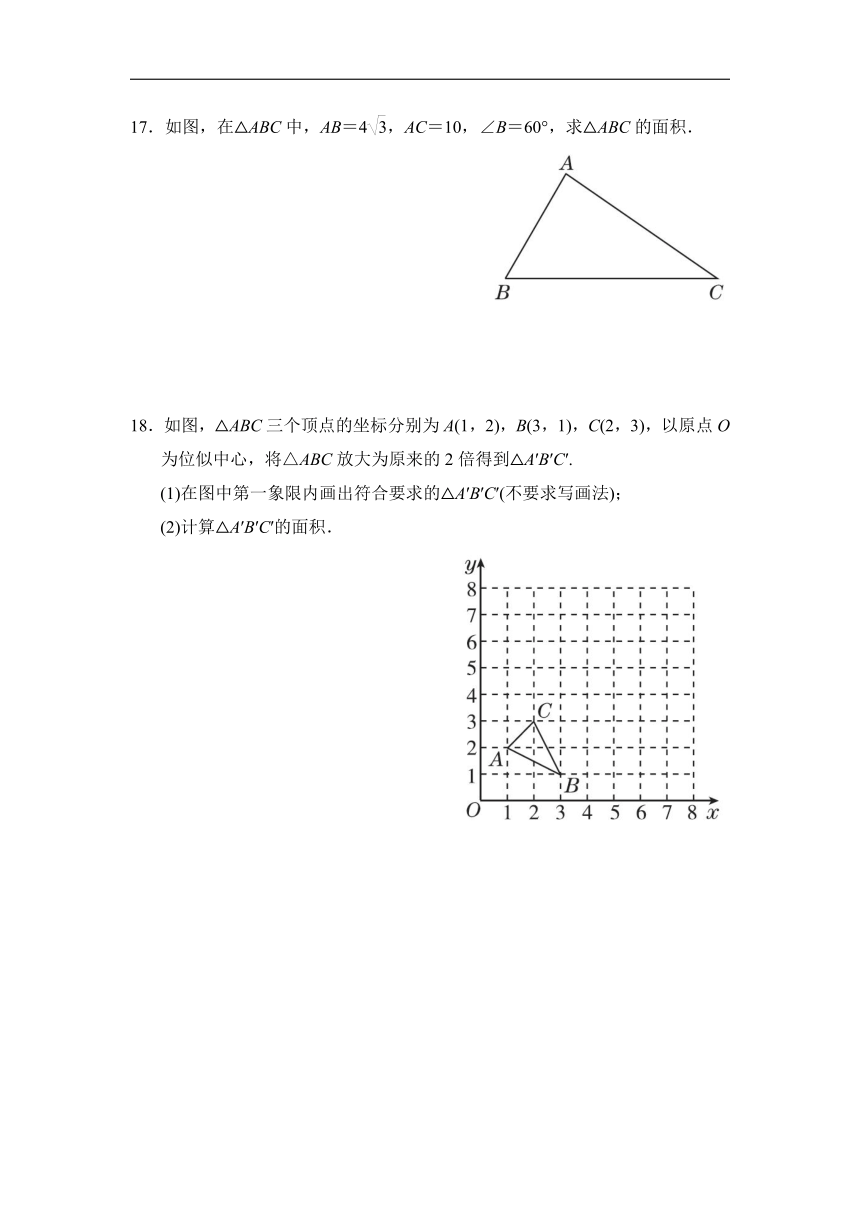
17.如图,在△ABC中,AB=4,AC=10,∠B=60°,求△ABC的面积.
18.如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得到△A′B′C′.
(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);
(2)计算△A′B′C′的面积.
19.如图,已知在正方形ABCD中,BE平分∠DBC,交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(1)求证:△BDG∽△DEG;
(2)若EG·BG=4,求BE的长.
20.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.
(1)求y1关于x的函数表达式,并画出这个函数的图象;
(2)若反比例函数y2=的图象与函数y1的图象相交于点A,且点A的纵坐标为2.
①求k的值;②结合图象,当y1>y2时,写出x的取值范围.
21.如图,某大楼DE的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=8米,AE=12米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,
参考数据:≈1.414,≈1.732)
22.某公司经销一种绿茶,每千克成本为50元.经市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体表达式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y元,解答下列问题:
(1)求y与x的函数表达式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2
250元的销售利润,销售单价应定为多少?
23.矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图①,已知折痕与边BC交于点O.
①
求证:△OCP∽△PDA;②
若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
答案
一、1.B 2.D
3.C 【点拨】∵a<0,∴抛物线的开口向下,①正确;抛物线y=-(x+2)2+3的对称轴为直线x=-2,②错误;顶点坐标为(-2,3),③正确;④抛物线开口向下,当x>2时,图象是下降趋势,y随x的增大而减小,④正确.故选C.
4.A 【点拨】在?ABCD中,AD=BC,AD∥BC,∵E是AD的中点,∴DE=AD=BC.由AD∥BC可得,△EDF∽△BCF.它们的周长比等于相似比,∴周长比等于ED?BC=BC:BC=1:2.故选A.
5.C 【点拨】∵在Rt△ABC中,∠ACB=90°,AC=,BC=2,
∴AB===3.
∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,
∠B+∠BCD=90°,∴∠ACD=∠B,
∴sin
∠ACD=sin
B==.
故选C.
6.C 【点拨】∵∠CPD=∠A,∠D=∠D,∴△ADP∽△PDG,∴∠APD=∠PGD,∴∠FPB=∠AGP.∵∠CPF=∠B,∠C=∠C,∴△CPF∽△CBP,∴∠CFP=∠CPB,∴∠PFB=∠APG;在△AGP和△BPF中,∠AGP=∠BPF,∠APG=∠BFP,∴△AGP∽△BPF.故选C.
7.B 8.B
9.B 【点拨】延长NP交EF于点G,设PG=x,则PN=4-x.
∵PG∥BF,∴△APG∽△ABF,
∴=,即=,
解得AG=2x,
∴PM=EG=EA+AG=2+2x,
∴S矩形PNDM=PM·PN=(2+2x)(4-x)=-2x2+6x+8=-2+(0≤x≤1),当x=1时,矩形PNDM的面积最大,最大值为12.故选B.
10.C 【点拨】连接AB,过点P作PC⊥AB于点C.设抛物线的对称轴与x轴的交点为点D.易求出抛物线的对称轴为直线x=,顶点A(,3),故BD=OD=,AD=3,在Rt△ABD中,tan∠BAD==,∴∠BAD=30°,∴PC=AP.
当O,P,C三点共线时,OP+PC的长最短,最短距离为sin∠OBC·OB=sin
60°×2
=3.
∴OP+AP的最小值为3.故选C.
二、11.2
12.(0,2)或(0,2)或或(0,8)
13.①②③ 【点拨】①∵图象开口向下,
∴a<0,
∵图象的对称轴在y轴左侧,
∴-<0,而a<0,∴b<0,
∵图象与y轴的交点在正半轴上,
∴c>0,∴abc>0,故结论正确.
②∵-2<x1<-1,
∴当x=-2时,y=4a-2b+c<0,故结论正确.
③∵-2<x1<-1,0<x2<1,
∴->-1,∵a<0,
∴2a-b<0,故结论正确.
故正确的结论有①②③.
14.①③④ 【点拨】∵△BCE沿BE折叠,点C恰好落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10.在Rt△ABF中,∵AB=6,BF=10,
∴AF==8,∴DF=AD-AF=10-8=2.设EF=x,则CE=x,DE=CD-CE=6-x.在Rt△DEF中,∵DE2+DF2=EF2,∴(6-x)2+22=x2,解得x=,∴DE=.∵△ABG沿BG折叠,点A恰好落在线段BF上的点H处,∴∠3=∠4,BH=BA=6,AG=HG,∴∠EBG=∠2+∠3=∠ABC=45°,∴①正确.HF=BF-BH=10-6=4,设AG=y,则GH=y,GF=8-y.在Rt△HGF中,∵GH2+HF2=GF2,∴y2+42=(8-y)2,解得y=3,∴AG=GH=3,GF=5.∵∠A=∠D,=,=,∴≠,∴△ABG与△DEF不相似,∴②错误.∵S△ABG=AB·AG=×6×3=9,S△FGH=GH·HF=×3×4=6,∴S△ABG=S△FGH,∴③正确.
∵AG+DF=3+2=5,而FG=5,∴AG+DF=FG,∴④正确.
三、15.解:原式=1-6×+4+-1=4-.
16.解:(1)联立
解得或
∴A(2,1),B.
(2)∵y=x2-4x+7=(x-4)2-1,
∴顶点C的坐标为(4,-1).
过顶点C作CD∥x轴交直线y=x于点D,如图.
在y=x中,令y=-1,得x=-1,解得x=-2,∴CD=6,
∴S△ABC=S△BCD-S△ACD=×6×-×6×(1+1)=7.5.
17.解:过点A作AD⊥BC于点D.
在Rt△ABD中,AD=AB·sin
B=4
×=6,
BD=AB·cos
B=4
×=2
.
在Rt△ACD中,CD===8,
∴BC=BD+CD=2
+8.
∴S△ABC=BC·AD=×(2+8)×6=6+24.
18.解:(1)如图.
(2)S△A′B′C′=4×4-×2×2-×2×4-×2×4=6.
19.(1)证明:∵BE平分∠DBC,
∴∠DBG=∠CBE,
根据旋转的性质,得∠EDG=∠CBE,
∴∠DBG=∠EDG,
又∵∠DGB=∠EGD,
∴△BDG∽△DEG.
(2)解:由(1)知△BDG∽△DEG,
∴=,∴DG2=EG·BG.
∵EG·BG=4,∴DG2=4,
∴DG=2(负值舍去).
∵∠EDG=∠CBE,∠DEG=∠BEC,
∴∠BGD=∠BCE=90°.
∴∠BGF=∠BGD=90°.
又∵BG=BG,∠DBG=∠FBG,
∴△DBG≌△FBG.
∴DG=FG,∴DF=2DG=4,
由题意可知,BE=DF,
∴BE=4.
20.解:(1)由题意得,y1=,即y1==
函数图象如图所示.
(2)①∵点A的纵坐标为2,点A在函数y1的图象上,∴=2,即x=±2.∴点A的坐标为(2,2)或(-2,2).∴k=±4.
②当k=4时,图象如图①,当y1>y2时,x的取值范围为x<0或x>2;
当k=-4时,图象如图②,当y1>y2时,x的取值范围为x<-2或x>0.
21.解:(1)过点B作BG⊥DE于点G,如图.
在Rt△ABH中,tan
∠BAH==,
∴∠BAH=30°,
∴BH=AB=4(米).
∴点B距水平面AE的高度BH为4米.
(2)由(1)知BH=4(米),
∴GE=BH=4(米),
AH=4
(米).
∴BG=HE=AH+AE=(4
+12)米.
在Rt△BGC中,∠CBG=45°,
∴CG=BG=(4
+12)米.
在Rt△ADE中,∠DAE=60°,AE=12米,
∴DE=AE·tan
∠DAE=12·tan
60°=12
(米).
∴CD=CG+GE-DE=4
+12+4-12
=16-8
≈16-8×1.732≈2.1(米).
∴广告牌CD的高度约为2.1米.
22.解:(1)由题意得y=(x-50)·w=(x-50)·(-2x+240)=-2x2+340x-12
000,
∴y与x的函数表达式为y=-2x2+340x-12
000.
(2)y=-2x2+340x-12
000=-2(x-85)2+2
450,
∴当x=85时,y的值最大.
(3)当y=2
250时,可得-2(x-85)2+2
450=2
250,
解这个方程,得x1=75,x2=95,
根据题意知,x=95不合题意,故舍去,
∴销售单价应定为75元/千克.
23.(1)①证明:如图,
∵四边形ABCD是矩形,
∴∠C=∠D=∠B=90°,
∴∠1+∠3=90°.
由折叠可得∠APO=∠B=90°,
∴∠1+∠2=90°.
∴∠3=∠2.
又∵∠C=∠D,
∴△OCP∽△PDA.
②解:∵△OCP与△PDA的面积比为1:4,且△OCP∽△PDA,
∴==.
∴CP=AD=4,AP=2OP.
设OP=x,则易得CO=8-x.
在Rt△PCO中,∠C=90°,
由勾股定理得
x2=(8-x)2+42.
解得x=5.
∴AB=AP=2OP=10.
(2)解:线段EF的长度不变.作MQ∥AN,交PB于点Q,如图.
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ.
又∵BN=PM,
∴BN=QM.
∵MQ∥AN,
∴∠QMF=∠BNF,∠MQF=∠FBN,
∴△MFQ≌△NFB.
∴QF=FB.
∴QF=QB.
∵MP=MQ,ME⊥PQ,
∴EQ=PQ.
∴EF=EQ+QF=PQ+QB=PB.
∵PC=4,BC=8,∠C=90°.
∴PB==4
,
∴EF=PB=2
.
∴动点M,N在移动的过程中,线段EF的长度不变,恒为2
.
一、选择题(每题4分,共40分)
1.已知a,d,c,b是成比例线段,其中a=3
cm,b=2
cm,c=6
cm,则d的长度为( )
A.4
cm
B.1
cm
C.9
cm
D.5
cm
2.在反比例函数y=图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k<0
B.k>0
C.k<1
D.k>1
3.对于抛物线y=-(x+2)2+3,有下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(-2,3);④当x>2时,y随x的增大而减小.其中正确结论的个数为( )
A.1
B.2
C.3
D.4
4.如图,在?ABCD中,E是AD边的中点,连接BE并延长交CD的延长线于点F,则△EDF与△BCF的周长之比是( )
A.1:2
B.1:3
C.1:4
D.1:5
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=,BC=2,则sin
∠ACD的值为( )
A.
B.
C.
D.
6.如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有( )
A.1对
B.2对
C.3对
D.4对
7.如图,在直角平面坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的相似比为的位似图形△OCD,则点C的坐标为( )
A.(-1,-1)
B.
C.
D.(-2,-1)
8.如图,在笔直的海岸线l上有A,B两个观测站,且AB=2
km.从A站测得船C在北偏东45°方向,从B站测得船C在北偏东22.5°方向,且tan
22.5°=-1,则船C离海岸线l的距离(即CD的长)为( )
A.4
km
B.(2+)km
C.2
km
D.(4-)km
9.如图,已知边长为4的正方形EFCD截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上找一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值为( )
A.8
B.12
C.
D.14
10.如图,在平面直角坐标系中,抛物线y=-x2+2
x的顶点为A,且与x轴的正半轴交于点B,点P为该抛物线对称轴上一点,则OP+AP的最小值为( )
A.
B.
C.3
D.2
二、填空题(每题5分,共20分)
11.如图,在由边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan
∠APD的值是________.
12.如图,点P是反比例函数y=(x>0)图象上一动点,在y轴上取点Q,使得以P,Q,O为顶点的三角形是含有30°角的直角三角形,则符合条件的点Q的坐标是________________.
13.如图是二次函数y=ax2+bx+c(a≠0)的图象,其与x轴的交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①abc>0;②4a-2b+c<0;③2a-b<0.其中正确的有____________(填序号).
14.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,使点C恰好落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,使点A恰好落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.其中正确的有____________(填序号).
三、解答题(15~18题每题8分;19,20题每题10分;21,22题每题12分;23题14分,共90分)
15.计算:(-1)2
022-6tan30°++|1-|.
16.已知抛物线y=x2-4x+7与直线y=x交于A,B两点(点A在点B左侧).
(1)求A,B两点的坐标;
(2)求抛物线顶点C的坐标,并求△ABC的面积.
17.如图,在△ABC中,AB=4,AC=10,∠B=60°,求△ABC的面积.
18.如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得到△A′B′C′.
(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);
(2)计算△A′B′C′的面积.
19.如图,已知在正方形ABCD中,BE平分∠DBC,交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(1)求证:△BDG∽△DEG;
(2)若EG·BG=4,求BE的长.
20.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.
(1)求y1关于x的函数表达式,并画出这个函数的图象;
(2)若反比例函数y2=的图象与函数y1的图象相交于点A,且点A的纵坐标为2.
①求k的值;②结合图象,当y1>y2时,写出x的取值范围.
21.如图,某大楼DE的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=8米,AE=12米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,
参考数据:≈1.414,≈1.732)
22.某公司经销一种绿茶,每千克成本为50元.经市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体表达式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y元,解答下列问题:
(1)求y与x的函数表达式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2
250元的销售利润,销售单价应定为多少?
23.矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.
(1)如图①,已知折痕与边BC交于点O.
①
求证:△OCP∽△PDA;②
若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.
答案
一、1.B 2.D
3.C 【点拨】∵a<0,∴抛物线的开口向下,①正确;抛物线y=-(x+2)2+3的对称轴为直线x=-2,②错误;顶点坐标为(-2,3),③正确;④抛物线开口向下,当x>2时,图象是下降趋势,y随x的增大而减小,④正确.故选C.
4.A 【点拨】在?ABCD中,AD=BC,AD∥BC,∵E是AD的中点,∴DE=AD=BC.由AD∥BC可得,△EDF∽△BCF.它们的周长比等于相似比,∴周长比等于ED?BC=BC:BC=1:2.故选A.
5.C 【点拨】∵在Rt△ABC中,∠ACB=90°,AC=,BC=2,
∴AB===3.
∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,
∠B+∠BCD=90°,∴∠ACD=∠B,
∴sin
∠ACD=sin
B==.
故选C.
6.C 【点拨】∵∠CPD=∠A,∠D=∠D,∴△ADP∽△PDG,∴∠APD=∠PGD,∴∠FPB=∠AGP.∵∠CPF=∠B,∠C=∠C,∴△CPF∽△CBP,∴∠CFP=∠CPB,∴∠PFB=∠APG;在△AGP和△BPF中,∠AGP=∠BPF,∠APG=∠BFP,∴△AGP∽△BPF.故选C.
7.B 8.B
9.B 【点拨】延长NP交EF于点G,设PG=x,则PN=4-x.
∵PG∥BF,∴△APG∽△ABF,
∴=,即=,
解得AG=2x,
∴PM=EG=EA+AG=2+2x,
∴S矩形PNDM=PM·PN=(2+2x)(4-x)=-2x2+6x+8=-2+(0≤x≤1),当x=1时,矩形PNDM的面积最大,最大值为12.故选B.
10.C 【点拨】连接AB,过点P作PC⊥AB于点C.设抛物线的对称轴与x轴的交点为点D.易求出抛物线的对称轴为直线x=,顶点A(,3),故BD=OD=,AD=3,在Rt△ABD中,tan∠BAD==,∴∠BAD=30°,∴PC=AP.
当O,P,C三点共线时,OP+PC的长最短,最短距离为sin∠OBC·OB=sin
60°×2
=3.
∴OP+AP的最小值为3.故选C.
二、11.2
12.(0,2)或(0,2)或或(0,8)
13.①②③ 【点拨】①∵图象开口向下,
∴a<0,
∵图象的对称轴在y轴左侧,
∴-<0,而a<0,∴b<0,
∵图象与y轴的交点在正半轴上,
∴c>0,∴abc>0,故结论正确.
②∵-2<x1<-1,
∴当x=-2时,y=4a-2b+c<0,故结论正确.
③∵-2<x1<-1,0<x2<1,
∴->-1,∵a<0,
∴2a-b<0,故结论正确.
故正确的结论有①②③.
14.①③④ 【点拨】∵△BCE沿BE折叠,点C恰好落在边AD上的点F处,
∴∠1=∠2,CE=FE,BF=BC=10.在Rt△ABF中,∵AB=6,BF=10,
∴AF==8,∴DF=AD-AF=10-8=2.设EF=x,则CE=x,DE=CD-CE=6-x.在Rt△DEF中,∵DE2+DF2=EF2,∴(6-x)2+22=x2,解得x=,∴DE=.∵△ABG沿BG折叠,点A恰好落在线段BF上的点H处,∴∠3=∠4,BH=BA=6,AG=HG,∴∠EBG=∠2+∠3=∠ABC=45°,∴①正确.HF=BF-BH=10-6=4,设AG=y,则GH=y,GF=8-y.在Rt△HGF中,∵GH2+HF2=GF2,∴y2+42=(8-y)2,解得y=3,∴AG=GH=3,GF=5.∵∠A=∠D,=,=,∴≠,∴△ABG与△DEF不相似,∴②错误.∵S△ABG=AB·AG=×6×3=9,S△FGH=GH·HF=×3×4=6,∴S△ABG=S△FGH,∴③正确.
∵AG+DF=3+2=5,而FG=5,∴AG+DF=FG,∴④正确.
三、15.解:原式=1-6×+4+-1=4-.
16.解:(1)联立
解得或
∴A(2,1),B.
(2)∵y=x2-4x+7=(x-4)2-1,
∴顶点C的坐标为(4,-1).
过顶点C作CD∥x轴交直线y=x于点D,如图.
在y=x中,令y=-1,得x=-1,解得x=-2,∴CD=6,
∴S△ABC=S△BCD-S△ACD=×6×-×6×(1+1)=7.5.
17.解:过点A作AD⊥BC于点D.
在Rt△ABD中,AD=AB·sin
B=4
×=6,
BD=AB·cos
B=4
×=2
.
在Rt△ACD中,CD===8,
∴BC=BD+CD=2
+8.
∴S△ABC=BC·AD=×(2+8)×6=6+24.
18.解:(1)如图.
(2)S△A′B′C′=4×4-×2×2-×2×4-×2×4=6.
19.(1)证明:∵BE平分∠DBC,
∴∠DBG=∠CBE,
根据旋转的性质,得∠EDG=∠CBE,
∴∠DBG=∠EDG,
又∵∠DGB=∠EGD,
∴△BDG∽△DEG.
(2)解:由(1)知△BDG∽△DEG,
∴=,∴DG2=EG·BG.
∵EG·BG=4,∴DG2=4,
∴DG=2(负值舍去).
∵∠EDG=∠CBE,∠DEG=∠BEC,
∴∠BGD=∠BCE=90°.
∴∠BGF=∠BGD=90°.
又∵BG=BG,∠DBG=∠FBG,
∴△DBG≌△FBG.
∴DG=FG,∴DF=2DG=4,
由题意可知,BE=DF,
∴BE=4.
20.解:(1)由题意得,y1=,即y1==
函数图象如图所示.
(2)①∵点A的纵坐标为2,点A在函数y1的图象上,∴=2,即x=±2.∴点A的坐标为(2,2)或(-2,2).∴k=±4.
②当k=4时,图象如图①,当y1>y2时,x的取值范围为x<0或x>2;
当k=-4时,图象如图②,当y1>y2时,x的取值范围为x<-2或x>0.
21.解:(1)过点B作BG⊥DE于点G,如图.
在Rt△ABH中,tan
∠BAH==,
∴∠BAH=30°,
∴BH=AB=4(米).
∴点B距水平面AE的高度BH为4米.
(2)由(1)知BH=4(米),
∴GE=BH=4(米),
AH=4
(米).
∴BG=HE=AH+AE=(4
+12)米.
在Rt△BGC中,∠CBG=45°,
∴CG=BG=(4
+12)米.
在Rt△ADE中,∠DAE=60°,AE=12米,
∴DE=AE·tan
∠DAE=12·tan
60°=12
(米).
∴CD=CG+GE-DE=4
+12+4-12
=16-8
≈16-8×1.732≈2.1(米).
∴广告牌CD的高度约为2.1米.
22.解:(1)由题意得y=(x-50)·w=(x-50)·(-2x+240)=-2x2+340x-12
000,
∴y与x的函数表达式为y=-2x2+340x-12
000.
(2)y=-2x2+340x-12
000=-2(x-85)2+2
450,
∴当x=85时,y的值最大.
(3)当y=2
250时,可得-2(x-85)2+2
450=2
250,
解这个方程,得x1=75,x2=95,
根据题意知,x=95不合题意,故舍去,
∴销售单价应定为75元/千克.
23.(1)①证明:如图,
∵四边形ABCD是矩形,
∴∠C=∠D=∠B=90°,
∴∠1+∠3=90°.
由折叠可得∠APO=∠B=90°,
∴∠1+∠2=90°.
∴∠3=∠2.
又∵∠C=∠D,
∴△OCP∽△PDA.
②解:∵△OCP与△PDA的面积比为1:4,且△OCP∽△PDA,
∴==.
∴CP=AD=4,AP=2OP.
设OP=x,则易得CO=8-x.
在Rt△PCO中,∠C=90°,
由勾股定理得
x2=(8-x)2+42.
解得x=5.
∴AB=AP=2OP=10.
(2)解:线段EF的长度不变.作MQ∥AN,交PB于点Q,如图.
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ.
又∵BN=PM,
∴BN=QM.
∵MQ∥AN,
∴∠QMF=∠BNF,∠MQF=∠FBN,
∴△MFQ≌△NFB.
∴QF=FB.
∴QF=QB.
∵MP=MQ,ME⊥PQ,
∴EQ=PQ.
∴EF=EQ+QF=PQ+QB=PB.
∵PC=4,BC=8,∠C=90°.
∴PB==4
,
∴EF=PB=2
.
∴动点M,N在移动的过程中,线段EF的长度不变,恒为2
.
同课章节目录
