第七章 随机变量及其分布列复习测试题A-2020-2021学年人教A版(2019)高中选择性数学必修三(Word含解析)
文档属性
| 名称 | 第七章 随机变量及其分布列复习测试题A-2020-2021学年人教A版(2019)高中选择性数学必修三(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-19 00:15:58 | ||
图片预览




文档简介
高二随机变量及其分布列复习测试题A
一.选择题(共8小题)
1.从标有1,2,3,4,5,6的6张卡片中,不放回地随机抽取两次,每次抽取一张.“在第一次抽到标号是4的条件下,第二次抽到的标号是奇数”的概率为
A. B. C. D.
2.若离型随机变量的分布列服从两点分布,且,,则
A. B. C. D.
3.一盒中有10个羽毛球,其中8个新的,2个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球的个数是一个随机变量,其分布列为,则的值为
A. B. C. D.
4.“四书”是《大学》《中庸》《论语》《孟子》的合称,又称“四子书”,在世界文化史、思想史上地位极高,所载内容及哲学思想至今仍具有积极意义和参考价值.为弘扬中国优秀传统文化,某校计划开展“四书”经典诵读比赛活动.某班有4位同学参赛,每人从《大学》《中庸》《论语》《孟子》这4本书中选取1本进行准备,且各自选取的书均不相同.比赛时,若这4位同学从这4本书中随机抽取1本选择其中的内容诵读,则抽到自己准备的书的人数的均值为
A. B.1 C. D.2
5.如图,某系统使用,,三种不同的元件连接而成,每个元件是否正常工作互不影响.当元件正常工作且,中至少有一个正常工作时系统即可正常工作.若元件,,正常工作的概率分别为0.7,0.9,0.8,则系统正常工作的概率为
A.0.196 B.0.504 C.0.686 D.0.994
6.若随机变量服从正态分布,,,则实数等于
A. B.0 C.1 D.2
7.已知的分布列为:
0 1
设,则的数学期望的值是
A. B. C.1 D.
8.2020年初,新型冠状肺炎在欧洲爆发后,我国第一时间内向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家.现有四个医疗小组甲、乙、丙、丁,和有4个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件 “4个医疗小组去的国家各不相同”,事件 “小组甲独自去一个国家”,则
A. B. C. D.
二.多选题(共4小题)
9.已知,分别为随机事件,的对立事件,(A),(B),则下列说法正确的是
A. B.
C.若,独立,则(A) D.若,互斥,则
10.骰子通常作为桌上游戏的小道具.最常见的骰子是六面骰,它是一个质地均匀的正方体,六个面上分别写有数字1,2,3,4,5,6.现有一款闯关游戏,共有4关,规则如下:在第关要抛掷六面骰次,每次观察向上面的点数并做记录,如果这次抛掷所出现的点数之和大于,则算闯过第关,,2,3,4.假定每次闯关互不影响,则
A.直接挑战第2关并过关的概率为
B.连续挑战前两关并过关的概率为
C.若直接挑战第3关,设 “三个点数之和等于15”, “至少出现一个5点”,则
D.若直接挑战第4关,则过关的概率是
11.连接正方体每个面的中心构成一个正八面体,甲随机选择此正八面体的三个顶点构成三角形,乙随机选择此正八面体三个面的中心构成三角形,且甲、乙的选择互不影响,则
A.甲选择的三个点构成正三角形的概率为
B.甲选择的三个点构成等腰直角三角形的概率为
C.乙选择的三个点构成正三角形的概率为
D.甲选择的三个点构成的三角形与乙选择的三个点构成的三角形相似的概率为
12.在庆祝教师节联欢活动中部分教职员工参加了学校工会组织的趣味游戏比赛,其中定点投篮游戏的比赛规则如下:①每人可投篮七次,每成功一次记1分;②若连续两次投篮成功加0.5分,连续三次投篮成功加1分,连续四次投篮成功加1.5分,以此类推,连续七次投篮成功加3分.假设某教师每次投篮成功的概率为,且各次投篮之间相互独立,则下列说法中正确的有
A.该教师恰好三次投篮成功且连续的概率为
B.该教师恰好三次投篮成功的概率为
C.该教师在比赛中恰好得4分的概率为
D.该教师在比赛中恰好得5分的概率为
三.填空题(共4小题)
13.已知甲、乙两球落入盒子的概率分别为和.假定两球是否落入盒子互不影响,则甲、乙两球至少有一个落入盒子的概率为 .
14.为迎接2022年北京冬奥会,某工厂生产了一批雪车,这批产品中按质量分为一等品,二等品,三等品.从这批雪车中随机抽取一件雪车检测,已知抽到不是三等品的概率为0.93,抽到一等品或三等品的概率为0.85,则抽到一等品的概率为 .
15.天津是一个古老与现代、保守与开放相融合的城市,历经600多年,特别是近代造就了中西合璧、古今兼容的独特城市风貌,成为国内外游客首选的旅游圣地.2021年元月份以来,来天津游览的游客络绎不绝,现通过对来津游客问卷调查,发现每位游客选择继续游玩的概率都是,不游玩的概率都是,若不游玩记1分,继续游玩记2分,游客之间选择意愿相互独立,从游客中随机抽取3人,记总得分为随机变量,则的数学期望 .
16.近年来,我国外卖业发展迅猛,外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线.他们根据外卖平台提供的信息到外卖店取单.某外卖小哥每天来往于个外卖店(外卖店的编号分别为1,2,,,其中,约定:每天他首先从1号外卖店取单,叫做第1次取单,之后,他等可能的前往其余个外卖店中的任何一个店取单叫做第2次取单,依此类推.假设从第2次取单开始,他每次都是从上次取单的店之外的个外卖店取单.设事件第次取单恰好是从1号店取单,是事件发生的概率,显然,,则 ,与的关系式为 .
四.解答题(共6小题)
17.某校从学生文艺部6名成员男2女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
18.已知盒中有形状、大小都相同的3个黑球和1个白球,每次从中取1个球,取到黑球记1分,取到白球记2分,有放回地抽取3次,用随机变量表示取3次所得的分数之和,求:
(1)3次都取到黑球的概率;
(2)随机变量的分布列.
19.在我国抗疫期间,素有“南抖音,北快手”之说的小视频除了给人们带来生活中的快乐外,更在于传递了一种正能量,为抗疫起到了积极的作用,但一个优秀的作品除了需要有很好的素材外,更要有制作上的技术要求,某同学学习利用“快影”软件将已拍摄的素材进行制作,每次制作分三个环节来进行,其中每个环节制作合格的概率分别为,,,只有当每个环节制作都合格才认为一次成功制作,该小视频视为合格作品.
(1)求该同学进行一次制作,小视频为合格作品的概率;
(2)求该同学进行3次制作,恰有一次合格作品的概率;
(3)若该同学制作4次,其中合格作品数为,求概率分布列.
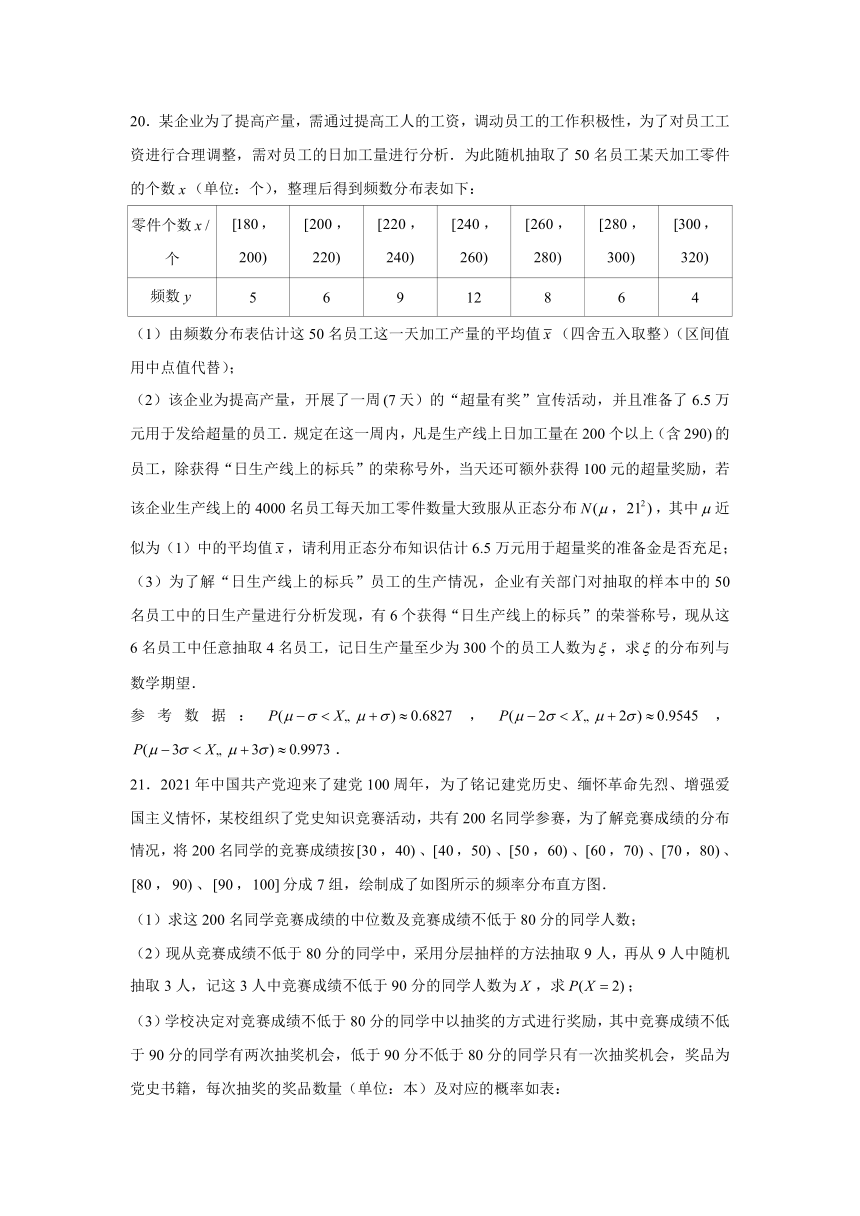
20.某企业为了提高产量,需通过提高工人的工资,调动员工的工作积极性,为了对员工工资进行合理调整,需对员工的日加工量进行分析.为此随机抽取了50名员工某天加工零件的个数(单位:个),整理后得到频数分布表如下:
零件个数个 , , , , , , ,
频数 5 6 9 12 8 6 4
(1)由频数分布表估计这50名员工这一天加工产量的平均值(四舍五入取整)(区间值用中点值代替);
(2)该企业为提高产量,开展了一周天)的“超量有奖”宣传活动,并且准备了6.5万元用于发给超量的员工.规定在这一周内,凡是生产线上日加工量在200个以上(含的员工,除获得“日生产线上的标兵”的荣称号外,当天还可额外获得100元的超量奖励,若该企业生产线上的4000名员工每天加工零件数量大致服从正态分布,,其中近似为(1)中的平均值,请利用正态分布知识估计6.5万元用于超量奖的准备金是否充足;
(3)为了解“日生产线上的标兵”员工的生产情况,企业有关部门对抽取的样本中的50名员工中的日生产量进行分析发现,有6个获得“日生产线上的标兵”的荣誉称号,现从这6名员工中任意抽取4名员工,记日生产量至少为300个的员工人数为,求的分布列与数学期望.
参考数据:,,.
21.2021年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某校组织了党史知识竞赛活动,共有200名同学参赛,为了解竞赛成绩的分布情况,将200名同学的竞赛成绩按,、,、,、,、,、,、,分成7组,绘制成了如图所示的频率分布直方图.
(1)求这200名同学竞赛成绩的中位数及竞赛成绩不低于80分的同学人数;
(2)现从竞赛成绩不低于80分的同学中,采用分层抽样的方法抽取9人,再从9人中随机抽取3人,记这3人中竞赛成绩不低于90分的同学人数为,求;
(3)学校决定对竞赛成绩不低于80分的同学中以抽奖的方式进行奖励,其中竞赛成绩不低于90分的同学有两次抽奖机会,低于90分不低于80分的同学只有一次抽奖机会,奖品为党史书籍,每次抽奖的奖品数量(单位:本)及对应的概率如表:
奖品数量(单位:本) 2 4
概率
现在从竞赛成绩不低于80分的同学中随机选一名同学,记其获奖书籍的数量为,求的分布列和数学期望.
22.2020年初,新型冠状病毒肺炎爆发时,我国政府迅速采取强有力措施抗击疫情,赢得了国际社会的高度评价.在这期间,为保证抗疫物资的质量,我国也加大了质量检查的力度.某市2020年初新增加了甲、乙两家专门生产消毒液的工厂,质检部门现从这两家工厂中各随机抽取了100瓶消毒液,检测其质量,得到甲厂所生产的消毒液的质量指标值的频率分布直方图如图所示,乙厂所生产的消毒液质量指标值的频数分布表如表所示(同一组数据用该组数据的区间中点值作代表,视频率为概率)
质量指标值 , , , , ,
频数 20 10 30 15 25
(1)规定:消毒液的质量指标值越高,消毒液的质量越好.已求得甲厂所生产的消毒液的质量指标值的中位数为,乙厂所生产的消毒液的质量指标值的平均数为26.5,分别求甲厂所生产的消毒液的质量指标值的平均数以及乙厂所生产的消毒液的质量指标值的中位数,并针对这两家工厂所生产的消毒液的质量情况写出两条统计结论;
(2)甲厂生产的消毒液的质量指标值近似地服从正态分布,其中近似为样本平均数,并已求得.该厂决定将消毒液分为,,三个等级,其中质量指标值不高于2.6的为级,高于38.45的为级,其余为级,甲厂近期生产了10万瓶消毒液,试估计其中级消毒液的总瓶数.
附:
,,
,
.
高二随机变量及其分布列复习测试题A
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:依题意,第一次取得4,故还有三个奇数,两个偶数,
故在第一次抽到标号是4的条件下,第二次抽到的标号是奇数的概率为,
故选:.
2.【解答】解:离型随机变量的分布列服从两点分布,且,
,
,
,
解得.
故选:.
3.【解答】解:从盒子中任取3个球来用,用完后装回盒中,此时盒中旧球个数,
即旧球的个数增加了2个,
取出的3个球中必有2个新球,
即取出的3个球必为1个旧球2个新球,
.
故选:.
4.【解答】解:记抽到自己准备的书的学生数为,则可能取值为0,1,2,4,
,
;
;
;
,
故选:.
5.【解答】解:某系统使用,,三种不同的元件连接而成,每个元件是否正常工作互不影响.
当元件正常工作且,中至少有一个正常工作时系统即可正常工作.
元件,,正常工作的概率分别为0.7,0.9,0.8,
则系统正常工作的概率为:
.
故选:.
6.【解答】解:随机变量服从正态分布,,,
可知与关于对称,
所以,即,
所以.
故选:.
7.【解答】解:由已知得,
,
,
,
.
故选:.
8.【解答】解:事件 “4个医疗小组去的国家各不相同”,事件 “小组甲独自去一个国家”,
则,(B),
,
故选:.
二.多选题(共4小题)
9.【解答】解:对于,,故选项正确;
对于,若,为独立事件是,则,
而(B)不一定等于,故选项错误;
对于,若,独立,则(A)(B),则,故选项正确;
对于,若,互斥,则,所以,故选项正确.
故选:.
10.【解答】解:对于,直接挑战第2关,则,
所以投掷两次点数之和应大于6,
故直接挑战第2关并过关的概率为,故选项正确;
对于,闯第1关时,,
所以挑战第1关通过的概率为,
则连续挑战前两关并过关的概率为,故选项错误;
对于,由题意可知,抛掷3次的基本事件有个,
抛掷3次至少出现一个5点的基本事件共有个,
故,
而事件包括:含5,5,5的1个,含4,5,6的有6个,一共有7个,
故,所以,故选正确;
对于,当时,,基本事件共有个,
“4 次点数之和大于20”包含以下情况:
含5,5,5,6的有4个,含5,5,6,6的有6个,含6,6,6,6的有1个,含4,6,6,6的有4个,
含5,6,6,6的有1个,含4,5,6,6的有12个,含3,6,6,6的有4个,
所以共有个,
所以直接挑战第4关,则过关的概率是,故选项正确.
故选:.
11.【解答】解:甲随机选择的情况有种,乙随机选择的情况有种,
对于,甲选择的三个点构成正三角形,只有一种情况:
甲从上下两个点中选一个,从中间四个点中选相邻两个,共有种,
故甲选择的三个点构成正三角形的概率为,故选项正确;
对于,甲选择的三个点构成等腰直角三角形,有三种情况:
①上下两点都选,中间四个点中选一个,共有种;
②上下两点钟选一个,中间四个点中选相对的两个点,共有种;
③中间四个点中选三个点,共有种,
故共有种,
所以甲选择的三个点构成等腰直角三角形的概率为,故选项正确;
对于,乙选择的三个点构成正三角形,只有一种情况:
上面四个面的中心中选一个点且从下面四个面的中心选相对的两个点,或下面四个面的中心中选一个点且从上面四个面的中心选相对的两个点,共有种,
所以乙选择的三个点构成正三角形的概率为,故选项错误;
对于,选择的三个点构成等腰直角三角形同上所求,共有种,概率为,
甲乙相似,则甲乙均为正三角形或均为等腰直角三角形,
所以甲选择的三个点构成的三角形与乙选择的三个点构成的三角形相似的概率为,故选项正确.
故选:.
12.【解答】解:对于,该教师恰好三次投篮成功且连续的概率,故正确;
对于,该教师恰好三次投篮成功的概率,故正确;
对于,该教师在比赛中恰好得4分包含的情况有:
①第1,3,5,7次投篮成功,另外三次投篮不成功,概率,
②连续三次投篮成功,另外四次投篮不成功,概率,
该教师在比赛中恰好得4分的概率为,故错误;
对于,教师在比赛中恰好得5分包含的情况有:
①四次发球成功,有两个连续两次投篮成功,概率,
②四次发球成功,有一个连续三次投篮成功三,
分别连续得分在首尾和不在首尾两类,概率,
教师在比赛中恰好得5分的概率为,故正确.
故选:.
三.填空题(共4小题)
13.【解答】解:甲、乙两球至少有一个落入盒子的概率为.
故答案为:.
14.【解答】解:设抽到一等品,二等品,三等品的事件分别为,,,
则,解得,
所以抽到一等品的概率为0.78.
故答案为:0.78.
15.【解答】解:的可能取值为3,4,5,6,
,,,,
所以.
故答案为:5.
16.【解答】解:第2次取单恰好是从1号店取单,
由于每天第1次取单都是从1号店开始,根据题意,第2次不可能从1号店取单,
所以,第3次取单恰好是从1号店取单,
因此,
.
故答案为:;.
四.解答题(共6小题)
17.【解答】解:(1)从6名成员中挑选2名成员,共有15种情况,记“男生甲被选中”为事件,事件所包含的基本事件数为5种,故.
(2)记“男生甲被选中”为事件,“女生乙被选中”为事件,则,由(1)知,故.
(3)记“挑选的2人一男一女”为事件,则,“女生乙被选中”为事件,,故.
18.【解答】解:(1)盒中有形状、大小都相同的3个黑球和1个白球,
每次从中取1个球,有放回地抽取3次,
3次都取到黑球的概率.
(2)用随机变量表示取3次所得的分数之和,
则的可能取值为3,4,5,6,
,
,
,
.
随机变量的分布列为:
3 4 5 6
19.【解答】解:(1)由题意知:制作一次视频成功的概率为:
.
(2)制作一次视频成功的概率为,
该同学进行3次制作,恰有一次合格作品的概率为:
.
(3)该同学制作4次,其中合格作品数为,根据题意,
,
,
,
,
,
的分布列为:
0 1 2 3 4
20.【解答】解:(1)由频数分布表得:,
(2)由(1)知,所以,,
所以,
因为,所以每天需奖励(元,
所以一周需奖励(元,所以6.5万元的准备金充足.
(3)由频数分布表可知,6个获得“日生产线上的标兵”荣誉称号中,日生产量至少为300个的员工有4名,
所以的可能值为2,3,4,
所以,,,
所以的分布列为
2 3 4
的数学期望为.
21.【解答】解:(1)因为,,
设这200名同学竞赛成绩的中位数为,则,解得,
竞赛成绩不低于80分的学生人数为.
(2)由题意可知,抽取的9人中,竞赛成绩不低于90分的学生人数为3,
所以;
(3)设这名同学获得数量为,则的可能取值为2,4,6,8,
,
,
,
,
2 4 6 8
.
22.【解答】解:(1)甲厂所生产的消毒液的质量指标值的平均数为,
设乙厂所生产的消毒液的质量指标值的中位数为,则,解得.
统计结论(答案不统一,任意两个即可)
①两家工厂生产的消毒液质量指标值的平均数相同,从这个角度看这两家工厂生产的消毒液质量基本相当;
②由数据波动的情况可知,乙厂生产的消毒液质量的方差大于甲厂生产的消毒液质量的方差,说明甲厂生产的消毒液比乙厂生产的消毒液的质量更稳定;
③两家工厂生产的消毒液质量指标值的平均数相同,但乙厂生产的消毒液质量的方差大于甲厂生产的消毒液质量的方程,所以甲厂生产的消毒液质量更好;
④两家工厂生产的消毒液质量指标值的众数相同,从这个角度看这两家工厂生产的消毒液质量基本相当;
⑤两家工厂生产的消毒液质量指标值的中位数相同,从这个角度看这两家工厂生产的消毒液质量基本相当;
⑥甲厂生产的消毒液质量集中在平均数附近,乙厂生产的消毒液质量指标值特别小和质量指标值特别大的较多,故甲厂生产的消毒液质量更好.
(2)由题意知,,,
所以,
所以估计级消毒液的总瓶数为瓶.
一.选择题(共8小题)
1.从标有1,2,3,4,5,6的6张卡片中,不放回地随机抽取两次,每次抽取一张.“在第一次抽到标号是4的条件下,第二次抽到的标号是奇数”的概率为
A. B. C. D.
2.若离型随机变量的分布列服从两点分布,且,,则
A. B. C. D.
3.一盒中有10个羽毛球,其中8个新的,2个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球的个数是一个随机变量,其分布列为,则的值为
A. B. C. D.
4.“四书”是《大学》《中庸》《论语》《孟子》的合称,又称“四子书”,在世界文化史、思想史上地位极高,所载内容及哲学思想至今仍具有积极意义和参考价值.为弘扬中国优秀传统文化,某校计划开展“四书”经典诵读比赛活动.某班有4位同学参赛,每人从《大学》《中庸》《论语》《孟子》这4本书中选取1本进行准备,且各自选取的书均不相同.比赛时,若这4位同学从这4本书中随机抽取1本选择其中的内容诵读,则抽到自己准备的书的人数的均值为
A. B.1 C. D.2
5.如图,某系统使用,,三种不同的元件连接而成,每个元件是否正常工作互不影响.当元件正常工作且,中至少有一个正常工作时系统即可正常工作.若元件,,正常工作的概率分别为0.7,0.9,0.8,则系统正常工作的概率为
A.0.196 B.0.504 C.0.686 D.0.994
6.若随机变量服从正态分布,,,则实数等于
A. B.0 C.1 D.2
7.已知的分布列为:
0 1
设,则的数学期望的值是
A. B. C.1 D.
8.2020年初,新型冠状肺炎在欧洲爆发后,我国第一时间内向相关国家捐助医疗物资,并派出由医疗专家组成的医疗小组奔赴相关国家.现有四个医疗小组甲、乙、丙、丁,和有4个需要援助的国家可供选择,每个医疗小组只去一个国家,设事件 “4个医疗小组去的国家各不相同”,事件 “小组甲独自去一个国家”,则
A. B. C. D.
二.多选题(共4小题)
9.已知,分别为随机事件,的对立事件,(A),(B),则下列说法正确的是
A. B.
C.若,独立,则(A) D.若,互斥,则
10.骰子通常作为桌上游戏的小道具.最常见的骰子是六面骰,它是一个质地均匀的正方体,六个面上分别写有数字1,2,3,4,5,6.现有一款闯关游戏,共有4关,规则如下:在第关要抛掷六面骰次,每次观察向上面的点数并做记录,如果这次抛掷所出现的点数之和大于,则算闯过第关,,2,3,4.假定每次闯关互不影响,则
A.直接挑战第2关并过关的概率为
B.连续挑战前两关并过关的概率为
C.若直接挑战第3关,设 “三个点数之和等于15”, “至少出现一个5点”,则
D.若直接挑战第4关,则过关的概率是
11.连接正方体每个面的中心构成一个正八面体,甲随机选择此正八面体的三个顶点构成三角形,乙随机选择此正八面体三个面的中心构成三角形,且甲、乙的选择互不影响,则
A.甲选择的三个点构成正三角形的概率为
B.甲选择的三个点构成等腰直角三角形的概率为
C.乙选择的三个点构成正三角形的概率为
D.甲选择的三个点构成的三角形与乙选择的三个点构成的三角形相似的概率为
12.在庆祝教师节联欢活动中部分教职员工参加了学校工会组织的趣味游戏比赛,其中定点投篮游戏的比赛规则如下:①每人可投篮七次,每成功一次记1分;②若连续两次投篮成功加0.5分,连续三次投篮成功加1分,连续四次投篮成功加1.5分,以此类推,连续七次投篮成功加3分.假设某教师每次投篮成功的概率为,且各次投篮之间相互独立,则下列说法中正确的有
A.该教师恰好三次投篮成功且连续的概率为
B.该教师恰好三次投篮成功的概率为
C.该教师在比赛中恰好得4分的概率为
D.该教师在比赛中恰好得5分的概率为
三.填空题(共4小题)
13.已知甲、乙两球落入盒子的概率分别为和.假定两球是否落入盒子互不影响,则甲、乙两球至少有一个落入盒子的概率为 .
14.为迎接2022年北京冬奥会,某工厂生产了一批雪车,这批产品中按质量分为一等品,二等品,三等品.从这批雪车中随机抽取一件雪车检测,已知抽到不是三等品的概率为0.93,抽到一等品或三等品的概率为0.85,则抽到一等品的概率为 .
15.天津是一个古老与现代、保守与开放相融合的城市,历经600多年,特别是近代造就了中西合璧、古今兼容的独特城市风貌,成为国内外游客首选的旅游圣地.2021年元月份以来,来天津游览的游客络绎不绝,现通过对来津游客问卷调查,发现每位游客选择继续游玩的概率都是,不游玩的概率都是,若不游玩记1分,继续游玩记2分,游客之间选择意愿相互独立,从游客中随机抽取3人,记总得分为随机变量,则的数学期望 .
16.近年来,我国外卖业发展迅猛,外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线.他们根据外卖平台提供的信息到外卖店取单.某外卖小哥每天来往于个外卖店(外卖店的编号分别为1,2,,,其中,约定:每天他首先从1号外卖店取单,叫做第1次取单,之后,他等可能的前往其余个外卖店中的任何一个店取单叫做第2次取单,依此类推.假设从第2次取单开始,他每次都是从上次取单的店之外的个外卖店取单.设事件第次取单恰好是从1号店取单,是事件发生的概率,显然,,则 ,与的关系式为 .
四.解答题(共6小题)
17.某校从学生文艺部6名成员男2女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
18.已知盒中有形状、大小都相同的3个黑球和1个白球,每次从中取1个球,取到黑球记1分,取到白球记2分,有放回地抽取3次,用随机变量表示取3次所得的分数之和,求:
(1)3次都取到黑球的概率;
(2)随机变量的分布列.
19.在我国抗疫期间,素有“南抖音,北快手”之说的小视频除了给人们带来生活中的快乐外,更在于传递了一种正能量,为抗疫起到了积极的作用,但一个优秀的作品除了需要有很好的素材外,更要有制作上的技术要求,某同学学习利用“快影”软件将已拍摄的素材进行制作,每次制作分三个环节来进行,其中每个环节制作合格的概率分别为,,,只有当每个环节制作都合格才认为一次成功制作,该小视频视为合格作品.
(1)求该同学进行一次制作,小视频为合格作品的概率;
(2)求该同学进行3次制作,恰有一次合格作品的概率;
(3)若该同学制作4次,其中合格作品数为,求概率分布列.
20.某企业为了提高产量,需通过提高工人的工资,调动员工的工作积极性,为了对员工工资进行合理调整,需对员工的日加工量进行分析.为此随机抽取了50名员工某天加工零件的个数(单位:个),整理后得到频数分布表如下:
零件个数个 , , , , , , ,
频数 5 6 9 12 8 6 4
(1)由频数分布表估计这50名员工这一天加工产量的平均值(四舍五入取整)(区间值用中点值代替);
(2)该企业为提高产量,开展了一周天)的“超量有奖”宣传活动,并且准备了6.5万元用于发给超量的员工.规定在这一周内,凡是生产线上日加工量在200个以上(含的员工,除获得“日生产线上的标兵”的荣称号外,当天还可额外获得100元的超量奖励,若该企业生产线上的4000名员工每天加工零件数量大致服从正态分布,,其中近似为(1)中的平均值,请利用正态分布知识估计6.5万元用于超量奖的准备金是否充足;
(3)为了解“日生产线上的标兵”员工的生产情况,企业有关部门对抽取的样本中的50名员工中的日生产量进行分析发现,有6个获得“日生产线上的标兵”的荣誉称号,现从这6名员工中任意抽取4名员工,记日生产量至少为300个的员工人数为,求的分布列与数学期望.
参考数据:,,.
21.2021年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某校组织了党史知识竞赛活动,共有200名同学参赛,为了解竞赛成绩的分布情况,将200名同学的竞赛成绩按,、,、,、,、,、,、,分成7组,绘制成了如图所示的频率分布直方图.
(1)求这200名同学竞赛成绩的中位数及竞赛成绩不低于80分的同学人数;
(2)现从竞赛成绩不低于80分的同学中,采用分层抽样的方法抽取9人,再从9人中随机抽取3人,记这3人中竞赛成绩不低于90分的同学人数为,求;
(3)学校决定对竞赛成绩不低于80分的同学中以抽奖的方式进行奖励,其中竞赛成绩不低于90分的同学有两次抽奖机会,低于90分不低于80分的同学只有一次抽奖机会,奖品为党史书籍,每次抽奖的奖品数量(单位:本)及对应的概率如表:
奖品数量(单位:本) 2 4
概率
现在从竞赛成绩不低于80分的同学中随机选一名同学,记其获奖书籍的数量为,求的分布列和数学期望.
22.2020年初,新型冠状病毒肺炎爆发时,我国政府迅速采取强有力措施抗击疫情,赢得了国际社会的高度评价.在这期间,为保证抗疫物资的质量,我国也加大了质量检查的力度.某市2020年初新增加了甲、乙两家专门生产消毒液的工厂,质检部门现从这两家工厂中各随机抽取了100瓶消毒液,检测其质量,得到甲厂所生产的消毒液的质量指标值的频率分布直方图如图所示,乙厂所生产的消毒液质量指标值的频数分布表如表所示(同一组数据用该组数据的区间中点值作代表,视频率为概率)
质量指标值 , , , , ,
频数 20 10 30 15 25
(1)规定:消毒液的质量指标值越高,消毒液的质量越好.已求得甲厂所生产的消毒液的质量指标值的中位数为,乙厂所生产的消毒液的质量指标值的平均数为26.5,分别求甲厂所生产的消毒液的质量指标值的平均数以及乙厂所生产的消毒液的质量指标值的中位数,并针对这两家工厂所生产的消毒液的质量情况写出两条统计结论;
(2)甲厂生产的消毒液的质量指标值近似地服从正态分布,其中近似为样本平均数,并已求得.该厂决定将消毒液分为,,三个等级,其中质量指标值不高于2.6的为级,高于38.45的为级,其余为级,甲厂近期生产了10万瓶消毒液,试估计其中级消毒液的总瓶数.
附:
,,
,
.
高二随机变量及其分布列复习测试题A
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:依题意,第一次取得4,故还有三个奇数,两个偶数,
故在第一次抽到标号是4的条件下,第二次抽到的标号是奇数的概率为,
故选:.
2.【解答】解:离型随机变量的分布列服从两点分布,且,
,
,
,
解得.
故选:.
3.【解答】解:从盒子中任取3个球来用,用完后装回盒中,此时盒中旧球个数,
即旧球的个数增加了2个,
取出的3个球中必有2个新球,
即取出的3个球必为1个旧球2个新球,
.
故选:.
4.【解答】解:记抽到自己准备的书的学生数为,则可能取值为0,1,2,4,
,
;
;
;
,
故选:.
5.【解答】解:某系统使用,,三种不同的元件连接而成,每个元件是否正常工作互不影响.
当元件正常工作且,中至少有一个正常工作时系统即可正常工作.
元件,,正常工作的概率分别为0.7,0.9,0.8,
则系统正常工作的概率为:
.
故选:.
6.【解答】解:随机变量服从正态分布,,,
可知与关于对称,
所以,即,
所以.
故选:.
7.【解答】解:由已知得,
,
,
,
.
故选:.
8.【解答】解:事件 “4个医疗小组去的国家各不相同”,事件 “小组甲独自去一个国家”,
则,(B),
,
故选:.
二.多选题(共4小题)
9.【解答】解:对于,,故选项正确;
对于,若,为独立事件是,则,
而(B)不一定等于,故选项错误;
对于,若,独立,则(A)(B),则,故选项正确;
对于,若,互斥,则,所以,故选项正确.
故选:.
10.【解答】解:对于,直接挑战第2关,则,
所以投掷两次点数之和应大于6,
故直接挑战第2关并过关的概率为,故选项正确;
对于,闯第1关时,,
所以挑战第1关通过的概率为,
则连续挑战前两关并过关的概率为,故选项错误;
对于,由题意可知,抛掷3次的基本事件有个,
抛掷3次至少出现一个5点的基本事件共有个,
故,
而事件包括:含5,5,5的1个,含4,5,6的有6个,一共有7个,
故,所以,故选正确;
对于,当时,,基本事件共有个,
“4 次点数之和大于20”包含以下情况:
含5,5,5,6的有4个,含5,5,6,6的有6个,含6,6,6,6的有1个,含4,6,6,6的有4个,
含5,6,6,6的有1个,含4,5,6,6的有12个,含3,6,6,6的有4个,
所以共有个,
所以直接挑战第4关,则过关的概率是,故选项正确.
故选:.
11.【解答】解:甲随机选择的情况有种,乙随机选择的情况有种,
对于,甲选择的三个点构成正三角形,只有一种情况:
甲从上下两个点中选一个,从中间四个点中选相邻两个,共有种,
故甲选择的三个点构成正三角形的概率为,故选项正确;
对于,甲选择的三个点构成等腰直角三角形,有三种情况:
①上下两点都选,中间四个点中选一个,共有种;
②上下两点钟选一个,中间四个点中选相对的两个点,共有种;
③中间四个点中选三个点,共有种,
故共有种,
所以甲选择的三个点构成等腰直角三角形的概率为,故选项正确;
对于,乙选择的三个点构成正三角形,只有一种情况:
上面四个面的中心中选一个点且从下面四个面的中心选相对的两个点,或下面四个面的中心中选一个点且从上面四个面的中心选相对的两个点,共有种,
所以乙选择的三个点构成正三角形的概率为,故选项错误;
对于,选择的三个点构成等腰直角三角形同上所求,共有种,概率为,
甲乙相似,则甲乙均为正三角形或均为等腰直角三角形,
所以甲选择的三个点构成的三角形与乙选择的三个点构成的三角形相似的概率为,故选项正确.
故选:.
12.【解答】解:对于,该教师恰好三次投篮成功且连续的概率,故正确;
对于,该教师恰好三次投篮成功的概率,故正确;
对于,该教师在比赛中恰好得4分包含的情况有:
①第1,3,5,7次投篮成功,另外三次投篮不成功,概率,
②连续三次投篮成功,另外四次投篮不成功,概率,
该教师在比赛中恰好得4分的概率为,故错误;
对于,教师在比赛中恰好得5分包含的情况有:
①四次发球成功,有两个连续两次投篮成功,概率,
②四次发球成功,有一个连续三次投篮成功三,
分别连续得分在首尾和不在首尾两类,概率,
教师在比赛中恰好得5分的概率为,故正确.
故选:.
三.填空题(共4小题)
13.【解答】解:甲、乙两球至少有一个落入盒子的概率为.
故答案为:.
14.【解答】解:设抽到一等品,二等品,三等品的事件分别为,,,
则,解得,
所以抽到一等品的概率为0.78.
故答案为:0.78.
15.【解答】解:的可能取值为3,4,5,6,
,,,,
所以.
故答案为:5.
16.【解答】解:第2次取单恰好是从1号店取单,
由于每天第1次取单都是从1号店开始,根据题意,第2次不可能从1号店取单,
所以,第3次取单恰好是从1号店取单,
因此,
.
故答案为:;.
四.解答题(共6小题)
17.【解答】解:(1)从6名成员中挑选2名成员,共有15种情况,记“男生甲被选中”为事件,事件所包含的基本事件数为5种,故.
(2)记“男生甲被选中”为事件,“女生乙被选中”为事件,则,由(1)知,故.
(3)记“挑选的2人一男一女”为事件,则,“女生乙被选中”为事件,,故.
18.【解答】解:(1)盒中有形状、大小都相同的3个黑球和1个白球,
每次从中取1个球,有放回地抽取3次,
3次都取到黑球的概率.
(2)用随机变量表示取3次所得的分数之和,
则的可能取值为3,4,5,6,
,
,
,
.
随机变量的分布列为:
3 4 5 6
19.【解答】解:(1)由题意知:制作一次视频成功的概率为:
.
(2)制作一次视频成功的概率为,
该同学进行3次制作,恰有一次合格作品的概率为:
.
(3)该同学制作4次,其中合格作品数为,根据题意,
,
,
,
,
,
的分布列为:
0 1 2 3 4
20.【解答】解:(1)由频数分布表得:,
(2)由(1)知,所以,,
所以,
因为,所以每天需奖励(元,
所以一周需奖励(元,所以6.5万元的准备金充足.
(3)由频数分布表可知,6个获得“日生产线上的标兵”荣誉称号中,日生产量至少为300个的员工有4名,
所以的可能值为2,3,4,
所以,,,
所以的分布列为
2 3 4
的数学期望为.
21.【解答】解:(1)因为,,
设这200名同学竞赛成绩的中位数为,则,解得,
竞赛成绩不低于80分的学生人数为.
(2)由题意可知,抽取的9人中,竞赛成绩不低于90分的学生人数为3,
所以;
(3)设这名同学获得数量为,则的可能取值为2,4,6,8,
,
,
,
,
2 4 6 8
.
22.【解答】解:(1)甲厂所生产的消毒液的质量指标值的平均数为,
设乙厂所生产的消毒液的质量指标值的中位数为,则,解得.
统计结论(答案不统一,任意两个即可)
①两家工厂生产的消毒液质量指标值的平均数相同,从这个角度看这两家工厂生产的消毒液质量基本相当;
②由数据波动的情况可知,乙厂生产的消毒液质量的方差大于甲厂生产的消毒液质量的方差,说明甲厂生产的消毒液比乙厂生产的消毒液的质量更稳定;
③两家工厂生产的消毒液质量指标值的平均数相同,但乙厂生产的消毒液质量的方差大于甲厂生产的消毒液质量的方程,所以甲厂生产的消毒液质量更好;
④两家工厂生产的消毒液质量指标值的众数相同,从这个角度看这两家工厂生产的消毒液质量基本相当;
⑤两家工厂生产的消毒液质量指标值的中位数相同,从这个角度看这两家工厂生产的消毒液质量基本相当;
⑥甲厂生产的消毒液质量集中在平均数附近,乙厂生产的消毒液质量指标值特别小和质量指标值特别大的较多,故甲厂生产的消毒液质量更好.
(2)由题意知,,,
所以,
所以估计级消毒液的总瓶数为瓶.
